cube numbers reasoning and problem solving

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Cube Numbers And Cube Roots

Cubes And Cube Roots

Here we will learn about cube numbers and cube roots including what a cube number is, what a cube root is, as well as how to cube a number and how to find the cube root of an integer. You’ll also learn how to solve problems by applying knowledge of cube numbers.

There are also cube numbers and cube roots worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a cube number?

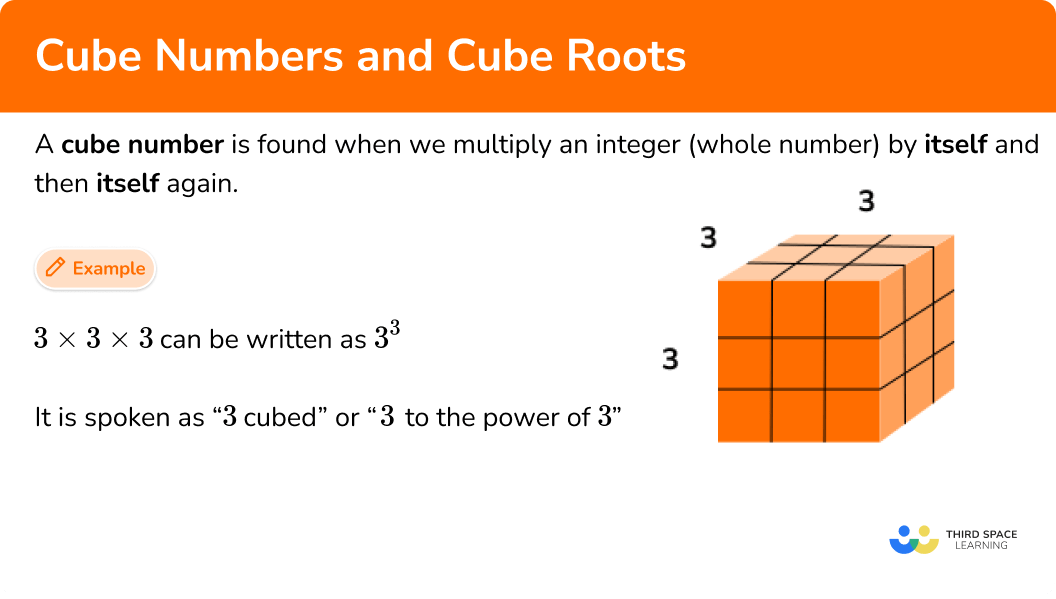
A cube number is found when we multiply an integer (whole number) by itself and then itself again . These are sometimes called ‘perfect cubes’ .

We can cube numbers with decimals but we do not refer to these as cube numbers. A given number / variable that is ‘ cubed ’ is multiplied by itself three times.

E.g. 4 × 4 × 4 can be written as 4 3 and is spoken as “4 cubed ” or “4 to the power of 3”  

A cube number is found when we multiply an integer (whole number) by itself,

Here are the first 10 cube numbers:

A cube number can be represented as an array which forms the shape of a cube that has a length 3 units, width 3 units and depth 3 units.

If we look at 3 3 , this is 3 × 3 × 3

Any cube number will form the shape of a cube.

Perfect cubes

The cube number of an integer is also called a perfect cube.

We can cube numbers with decimal places but we do not refer to these as cube numbers or perfect cubes.

A given number or variable that is ‘cubed’ is multiplied by itself and this applies to decimals as to integers.

It’s relatively straightforward to work out the cube root of a perfect cube but it is a much harder process to work out decimal cube roots. You quickly end up working with surds and irrational numbers .

Cubing negative numbers

We can also cube negative numbers. E.g.

You will notice that when we cube a negative number we get a negative number . This is because a negative number multiplied by a negative number multiplied by a negative number gives us a negative result. Learn more by reviewing our lesson on negative numbers.

When we cube negative 5 we get the negative answer of the cube of positive 5 . This is true for all numbers (and variables) and means:

What is a cube root?

The cube root of a number is a value that can be multiplied by itself three times to give the original number. A cube root is the inverse operation of cubing a number. The cube root symbol looks like this 3 √

When we cube a positive number we get a positive result and when we cube a negative number we get a negative result. So the cube root of a positive number is also a positive number , and the cube root of a negative number is also a negative number .

Cube numbers worksheet

Get your free cube numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on   powers and roots

Cube numbers and cube roots  is part of our series of lessons to support revision on  powers and roots . You may find it helpful to start with the main powers and roots lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Powers and roots
• Square numbers and square roots
• To the power of
• Fractional powers
• Negative powers
• Expressing a power with a different base

A single number (constant) or variable 

E.g. in the expression 4x − 7 both 4x and − 7 are terms

Coefficient

The number which the variable is being multiplied by

E.g. in 2x 3 the coefficient is 2

A whole number

E.g. 1, 7 or 1003

Index (also called exponent or powers)

The index number is the amount of times you multiply a number/variable by itself.

E.g. the index number in 5 3 is 3

Note: the plural of index is indices 

Note: you will see index number as a superscript

Base number

The number/unknown that is being multiplied by itself an amount of times

E.g. the base number in 5 3 is 5 and in 2x 3 the base number is x

Advanced vocabulary –  only for Additional Maths, A-Level

Real numbers

Any positive or negative number is called a real number. Numbers that are not ‘real’ are called imaginary numbers. Integers, decimals, fractions are all examples of real numbers

E.g. 1, 2, 5 and 100 are all examples of a positive real numbers

-1, -2, -50 and -65.67 are all examples of a negative real number

Imaginary numbers

Numbers that are not real are called imaginary numbers, for example you will notice we cannot find the square root of a negative number (try it on a calculator), this because it is an imaginary number.. Numbers that contain an imaginary part and real part are called complex numbers.

Cube numbers and cube roots examples

What is 5 cubed?

5 cubed means 5 × 5 × 5

So 5 cubed is 1 25

What is 9 cubed?

9 3 cubed means 9 × 9 × 9

So 9 cubed is 729

What is the cube root of 64 ?

The cube root of 64 means what value can be multiplied by itself three times to give 64

How to use cube numbers and cube roots

Identify whether you need to cube or cube root the number/variable

Perform the operation

• Clearly state the answer within the context of the question e.g. including units

Now you will focus on solving problems using your knowledge of cube numbers and cube roots.

Explain how to solve problems involving cube numbers and cube roots in 3 steps

Cubes and cube roots problem examples

Example 4: knowledge of cube numbers.

Danny says 2 cubed is 6 . Why is Danny wrong? What mistake did he make?

The question focus is on cubing 2 or “ 2 cubed”

2 Perform the operation

3 Clearly state the answer within the context of the question

Danny is wrong because 2 cubed is 8 not 6 .

The mistake Danny made was he did ‘2 × 3’ not ‘2 3 ’ .

Example 5: problem solving with cube roots

Ava says the cube root of an integer is always smaller than the original number. Prove Ava is incorrect.

You are looking for a relationship between the cube root of an integer and the original number. It will help to write down your cube numbers and their cube roots.

Clearly state the answer within the context of the question

Ava is incorrect because

The answer here is not smaller than the original number.

Example 6: solving problems involving cube numbers

The sum of two cube numbers is 72 . Find the two cube numbers.

Remember sum means add. Therefore you are looking for two cube numbers that add together to make 72 .

It will help here to list the cube numbers up to 72

The Cube Numbers: 1     8     27     64

You now need to pick two of these numbers that when added together make 72

The two cube numbers are 64 and 8 .

Example 7: cube numbers within a 3D polygon

A cube has a volume of 125 mm 3 . What is the length of one side?

The volume of a cube is found by multiplying the length, width and height together. For a cube the length, width and height are the same length.

Therefore you are looking for a number that when multiplied by itself three times (or cubed) is equal to 125 .

Therefore you need to find the cube root of 125

Therefore the length of the cube is 5 mm.

Example 8: cube numbers within a 3D polygon

Length of one side of a cube is 4 mm. What is the volume of the cube?

Therefore you are are going to multiply the side length by itself three or ‘cube’ the length.

Therefore you need to cube 4

Therefore the volume of the cube is 64 mm 3 .

Lexi says “when you add three consecutive cube numbers, the answer is always odd.”

Is Lexi right? Explain your answer.

To prove Lexi wrong we only need to find one example where she is incorrect, this is sometimes known as proof by contradiction.

Therefore we are looking for 3 consecutive cube numbers that when added together are even. It will be helpful here to list the ‘main’ cube numbers.

The cube numbers:

You are now looking for one example where three of these numbers when added together make an even number.

For example: 1 + 8 + 27 = 36

Lexi is wrong because 1 + 8 + 27 = 36

Common misconceptions

• Cube numbers

Incorrect understanding of cubing a number E.g. 3 3 = 27 not 9

Not recognising that a negative number cube rooted is negative E.g. \sqrt[3]-8 = -2

Practice cube numbers and cube roots questions

1. What is 10 cubed?

2. What is the value of the cube root of 216?

3. What is (-7)^3?

4. What is the value of \sqrt[3]{-1}?

5. The sum of two cube numbers is 65 . Find the two cube numbers.

The cube numbers up to 65 are 1, 8, 27, 64.

The two that add up to 65 are 1 and 64.

6. A cube has a volume of 512 cm ^3 . What is the length of one side?

We find the volume of a cube by multiplying the length, the width and the height together.

These are all equal for a cube so we need to find a number that, when multiplied by itself three times, gives us 512.

Therefore we need to find the cube root of 512.

Cube numbers and cube roots GCSE questions

1.  Work out the value of:

(a)    3^{3} 

(b)    5 \times 2^{3}

(c)    6^{3} − 3^{3}

(a)    3 \times 3 \times 3

(b)    5 \times 8

(c)    216 – 27

2. Here is a list of numbers:

(a)    List the cube numbers

(b)    Which number is a square and cube number?

(a)    1000, 8 , 64 and 1

3. Find the value of:

(a)    \sqrt[3]{729} 

(b)    \sqrt[3]{-1}

(c)    \sqrt[3]{-8}

4. Simplify the following expression

Correct coefficient

Correct x  (or x^{1} )

Learning checklist

You have now learned how to:

• Calculate cube numbers up to 10 × 10 × 10
• Use positive integer powers and their associated real roots
• Recognise and use the cube numbers
• Apply properties of cubes to a context

The next lessons are

• Converting fractions, decimals and percentages
• Standard form
• Simple interest and compound interest

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Cube Numbers – Definition, Examples, Facts, Practice Problems

What are cube numbers, why are they called cube numbers, cube numbers vs. square numbers, solved examples on cube numbers, practice problems on cube numbers, frequently asked questions on cube numbers.

We know that a “number squared” refers to the product of the number with itself. So, to find a square, we simply multiply the number with itself once.

What is a cubed number? A “number cubed” refers to the multiplication of the number with itself and again by itself, i.e., multiplication of the same number two times.

In other words, we can find the cube of a number by multiplying the square of a number by the number itself.

A cube number is obtained by raising a given number to the power of 3. 

Thus, for a given number n, the cube number is “n cubed” or “ $n^3$ .”

Cube Numbers Definition

A cube number is the result of the product of three identical numbers.

A cube number is the number raised to the power of 3. 

A cube number is the result of multiplication of a number with itself twice.

n cubed $= n^3 = n \times n \times n$

Cube numbers of positive numbers are positive. 

Cube numbers of negative numbers are negative.

Examples of cube numbers:

$(-2)^3 = (-2)\times(-2)\times(-2) =\;-8$

$6^3 = 6\times6\times6 = 216$

$10^3 = 10\times10\times10 = 1000$

$(-10)^3 = (-10)\times(-10)\times(-10) = -1000$

The best example of a cube number in geometry is the volume of a cube.

A cube is a three-dimensional shape or a geometric solid. All its sides are equal in length. 

The volume of a cube with side “s” is given by $s^3$ or “side cubed.”

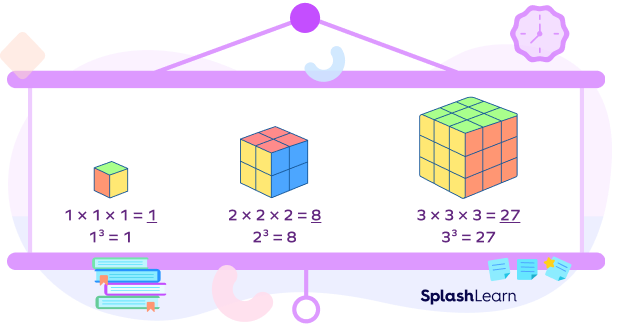
Volume of a cube with side 1 unit $= 1^3 = 1$

Volume of a cube with side 2 units $= 2^3 = 8$

Volume of a cube with side 3 units $= 3^3 = 27$

Since a cube is a three-dimensional shape with the same length, width, and height of its sides, its volume can be calculated by “cubing” its length.

A cube with side-length 1 unit is called a unit cube. If “n” such unit cubes perfectly fit inside a given cube, then we say that the volume of a given cube is “n cubic units.”

Related Worksheets

List of Cube Numbers From 1 to 100

How to cube numbers.

To cube numbers, simply multiply the square of a number by itself.

The standard form of a cube of any number “a” is “$a^3$,” which can be obtained using $a^3 = a\times a \times a$. This applies to every number. 

For example, $3 \times 3 \times 3 = 27,\; 8 \times 8 \times 8 = 512,\; 10 \times 10 \times 10 = 1000$, etc.

The cube numbers are the numbers obtained by raising a number to the power of 3, whereas a square is obtained by multiplying a number by itself.

Square of $n = n^2 = n \times n$   …a number multiplied by itself once

Cube of $n = n^3 = n \times n \times n$ …a number multiplied by itself twice

Let us consider an example. 

Multiply 4 by itself to get its square.

4 squared $= 4^2 = 4\times4 = 16$ …4 multiplied by itself once

Multiplying 42 by 4, we get

4 cubed $= 4^3 = 4\times4\times4 = 64$ …4 multiplied by itself twice

Here, 64 is a cube number. 

Cube Numbers in Real Life

While cube numbers are excellent for assisting students in comprehending patterns and relationships between numbers, they also have practical applications. Let’s say we want to know the volume of a cubic object like a container; all we need to do is cube the value of one of its sides.

To determine the dimensions of gift boxes, size of ice cubes, etc., are a few of the many real-life uses for cube numbers.

Facts about Cube Numbers

• The last digits of a cube number are 1, 2, 3, 4, 6, 7, 8, 9, 000, and 125, 375, 625, or 875.
• The Rubik’s Cube is a cube of number 3.
• The result of the cube of even numbers will be an even number. For example, $4^3 = 64,\; 6^3 = 216$, etc.
• The result of the cube of odd numbers will be an odd number. For example, $3^3 = 27,\; 5^3 = 125$, etc.
• The sum of consecutive odd numbers can be used to describe perfect cube numbers. For example, 27 is a cube number of 3, and it can be written as the sum of the consecutive odd numbers as $7 + 9 + 11 = 27$, similarly $64 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15$, etc.
• A cube number represents the volume of a cube.

In this article, we have learned about cube numbers, their visualization, list, and examples. Let’s solve a few examples and practice problems.

• Find out the cube of numbers $9,\; -15$ , and 19.

Cube of numbers 9, 15, and 19 calculated as

$9^3 = 9 \times 9 \times 9 = 929$

$(-15)^3 = (-15) \times (-15) \times (-15) = 3375$

$19^3 = 19 \times 19 \times 19 = 6859$

• Evaluate $25^3$ .

$25^3 = 25 \times 25 \times 25$

      $= 625 \times 25$

      $= 15625$

• Write the cube number 64 and 125 as the sum of the consecutive odd numbers.

64 and 125 as the sum of the consecutive odd numbers can be written as 

$64 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15$

$125 = 21 + 23 + 25 + 27 + 29$.

• If the side length of a cube is 12 units, find its volume.

The volume of a cube can be calculated by “cubing” its side length.

The side length of a cube $= 12$ units

$\therefore$ Volume $= 12^3 = 12 \times 12 \times 12$

 $= 1728$ cubic units.

• Explain why the number 512 is a cube number.

The number 512 can be written as $512 = 8 \times 8 \times 8$.

Here, the result of multiplying the number 8 by itself and then by itself again is 512.

And a cube number is defined as the result of multiplying a number by itself and then by itself again. Thus, 512 is a cube number.

Cube Numbers - Definition, Examples, Facts, Practice Problems

Attend this quiz & Test your knowledge.

Which of the following is a cube number?

$3^3 + 6^3 =$ ______., a perfect cube can be expressed as the ____ of a cube., the cube of a negative number is _______..

Is 343 a cube number?

Yes, 343 is a cube number as it can be written as $343^3 = 7 \times 7 \times 7$.

Are there any negative cube numbers?

Yes, cubes of negative numbers are negative cube numbers. For example, $(−2)^3 = −8,\; (−3)^3 = −27,\; (−4)^3 = −64$, etc.

What is the cube of $−5$ ?

Cube of $−5 = (−5)^3 = −125$.

How many perfect cube numbers are there between 1 and 500?

Perfect cube numbers between 1 and 500 are 1, 8, 27, 64, 125, 216, and 343.

Hence, there are a total of eight perfect cube numbers between 1 and 500.

How many perfect cube numbers are there between 1 and 100 which are also a perfect square?

Perfect cube numbers between 1 and 100 are 1, 8, 27, and 64, out of which only 1 and 64 are perfect squares.

What is 1 cubed?

1 cubed $= 1^3 = 1$

RELATED POSTS

• Height of Equilateral Triangle – Formula, Method, Examples
• Addition Property of Equality: Definition, Formula, Examples
• Types of Angles – Definition with Examples
• Area of an Equilateral Triangle – Formula, Derivation, Examples
• Math Glossary Terms beginning with Z

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Cube Numbers and Cube Roots Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2014 Revised 2018

Take Some ... Cubes

Square and Cube Numbers

By the end of this unit, students will be able to:

• Understand the concepts of square and cube numbers.
• Identify square and cube numbers and their properties.
• Recognize number patterns related to square and cube numbers.
• Apply knowledge of square and cube numbers to solve problems and analyze patterns.

What's Included

• Three-part Lesson
• Self-marking Activities
• Fluency, Reasoning and Problem-solving Questions.
• Engaging Drag and Drop Activities
• Interactive Self-marking Worksheet
• Printable Worksheets to Consolidate Learning

Year 6 Number: addition-subtraction-multiplication-and-division

• solve problems involving addition, subtraction, multiplication and division
• England & Wales: Year 6
• Scotland: Primary 6
• Rep. Ireland: Fifth Class
• Australia: Grade 5
• USA: Grade 5

Connected Resources

Multiplying Decimals-Single Digits

Short Divisions

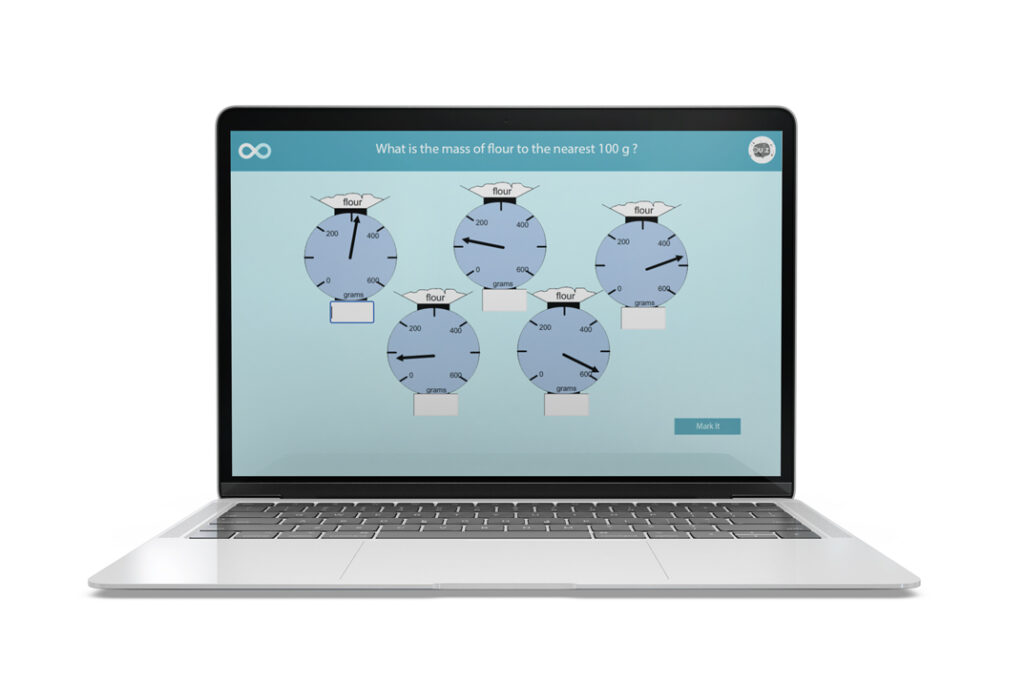
Using Estimation to Check Answers

Prime and Composite Numbers

Hear from other teachers.

Ok, I get the point!

Get unlimited access to the entire library of resources., connect with us, quick links.

• Explore Maths
• Explore Science
• Explore English

• Home Learning
• Free Resources
• New Resources
• Free resources
• New resources
• Filter resources
• Childrens mental health
• Easter resources

Internet Explorer is out of date!

For greater security and performance, please consider updating to one of the following free browsers

Cube Numbers Lesson

This  Year 5 Cube Numbers  lesson covers the prior learning of calculating square numbers, before moving onto the main skill of calculating cube numbers.

The lesson starts with a prior learning worksheet to check pupils’ understanding. The interactive lesson slides recap the prior learning before moving on to the main skill. Children can then practise further by completing the activities and can extend their learning by completing an engaging extension task.

National Curriculum Objective Mathematics Year 5: (5C5d)  Recognise and use square numbers and cube numbers, and the notation for squared (2) and cubed (3)

Get the most from lessons!

Resources for teachers

Interactive activities for children

2 Teaching Support

Subscription

Lesson Slides

These lesson slides guides pupils through the prior learning of calculating square numbers, before moving onto the main skill of cube numbers. There are a number of questions to check pupils' understanding throughout.

Modelling PowerPoint

This powerpoint can be used to model the questions that the children will complete on the Varied Fluency and Reasoning & Problem Solving worksheets as part of this lesson.

These are the same as the lesson slides on Classroom Secrets. You can assign this as an activity for pupils to access individually in school or remotely from home.

Video Tutorial

In this Cube Numbers Video Tutorial, Ivan discusses what cube numbers are, and how to use them in calculations, including with knowledge of the order of operations.

1 Prior Learning

This Year 5 Cube Numbers lesson covers the prior learning of calculating square numbers, before moving onto the main skill of calculating cube numbers.

In this Square Numbers Video Tutorial, Jade demonstrates square numbers and uses squared notation.

Interactive Activity

This Year 5 Square Numbers activity checks your child’s understanding of identifying square numbers.

2 Practical Activities

Supporting Activities

This fractions on a number line supporting activities sheet contains suggestions for additional tasks you might wish to use to support pupils' understanding of the concepts taught in the lesson.

2 Varied Fluency

This differentiated worksheet includes varied fluency questions for pupils to practise the main skill of this lesson.

Flash Cards Activity

This Year 5 Cube Numbers Flash Cards Game checks pupils’ understanding of cube numbers.

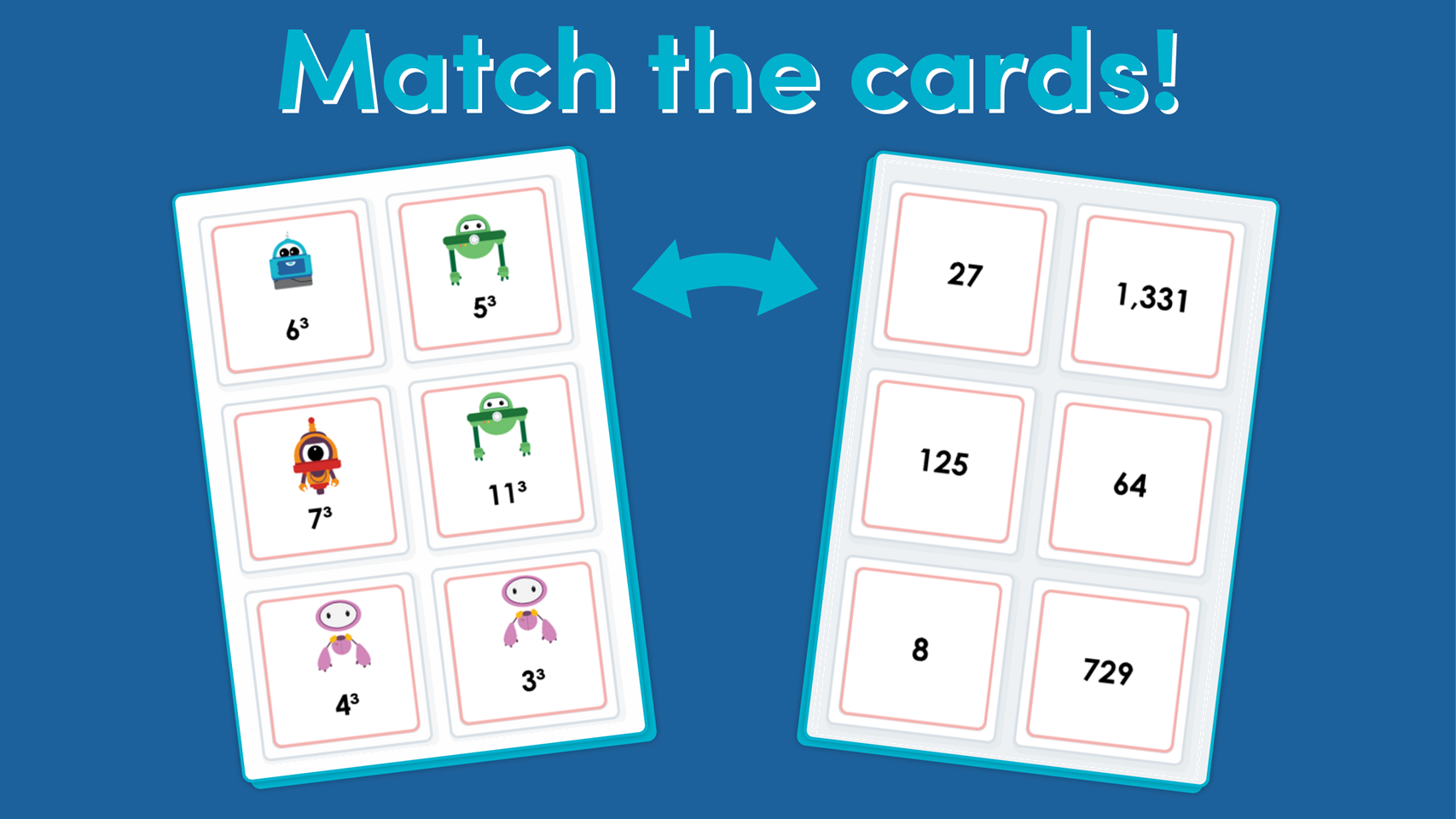
This Year 5 Cube Numbers Matching Game checks pupils’ understanding of cube numbers.

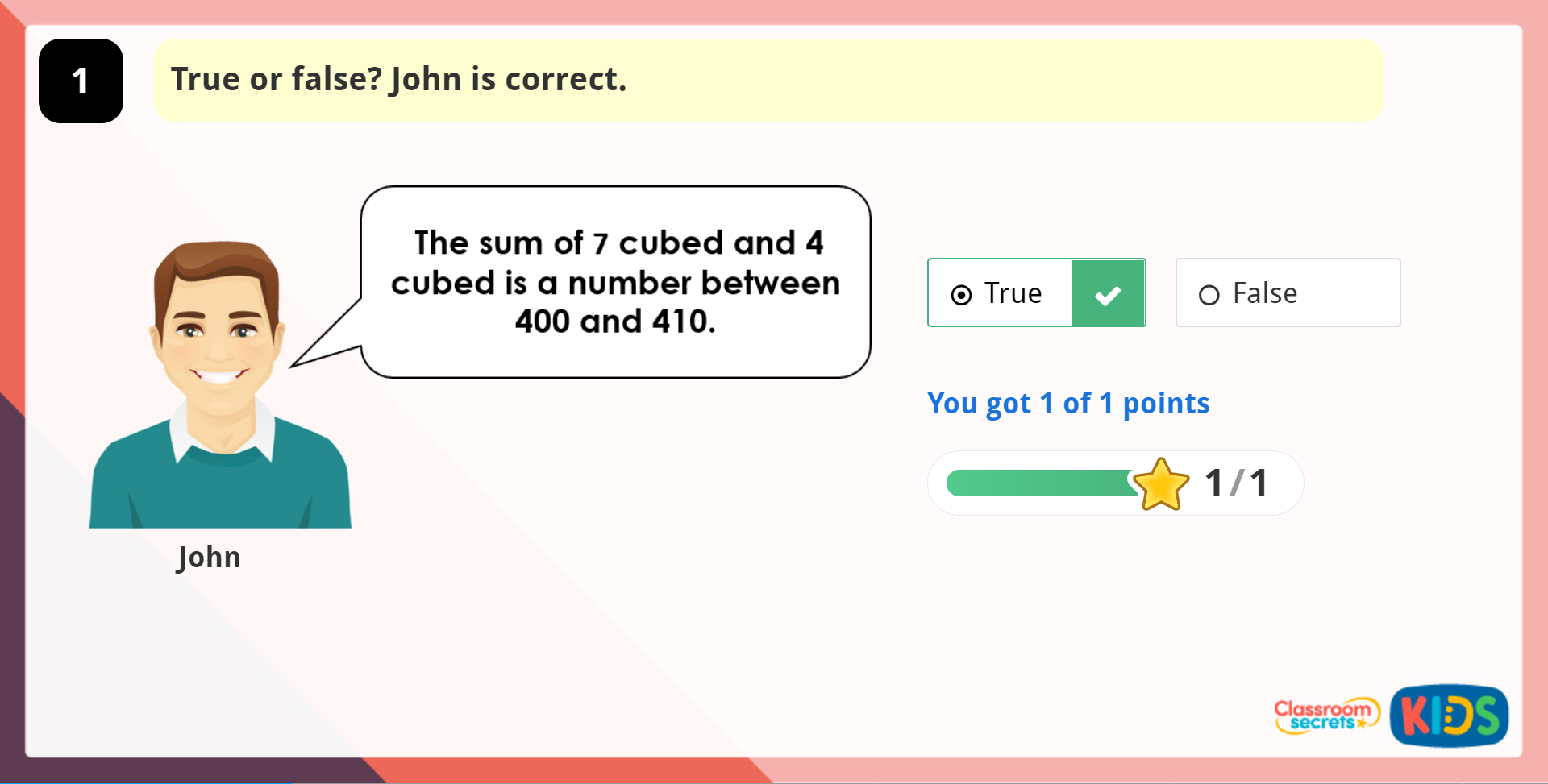
This Year 5 Cube Numbers Game checks pupils’ understanding of cube numbers.

2 Application

This cube numbers extension task includes a challenge activity which can be used to further pupils' understanding of the concepts taught in the cube numbers lesson.

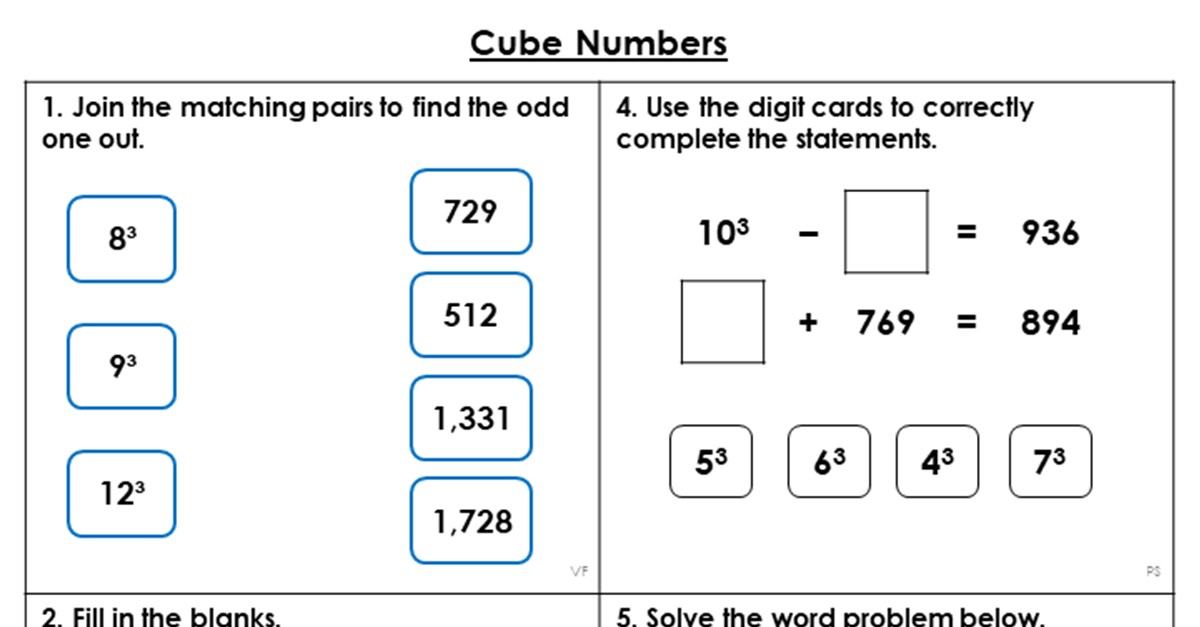
Mixed Practice

This worksheet includes varied fluency, reasoning and problem solving questions for pupils to practise the main skill of cube numbers.

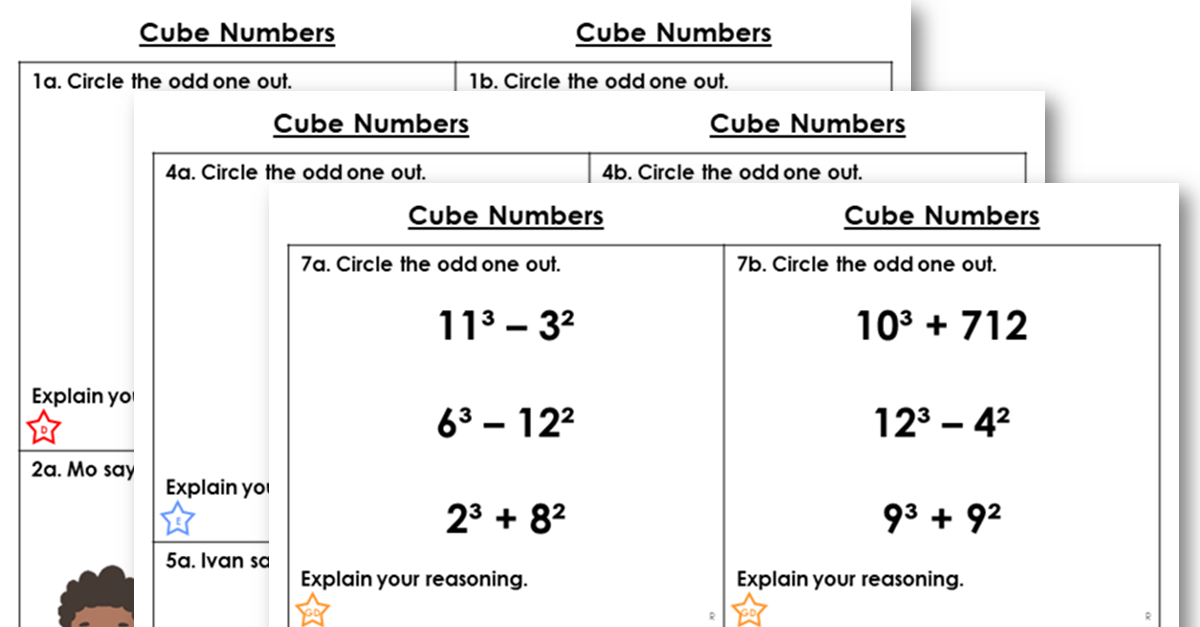
This differentiated worksheet includes reasoning and problem solving questions to support the teaching of this step.

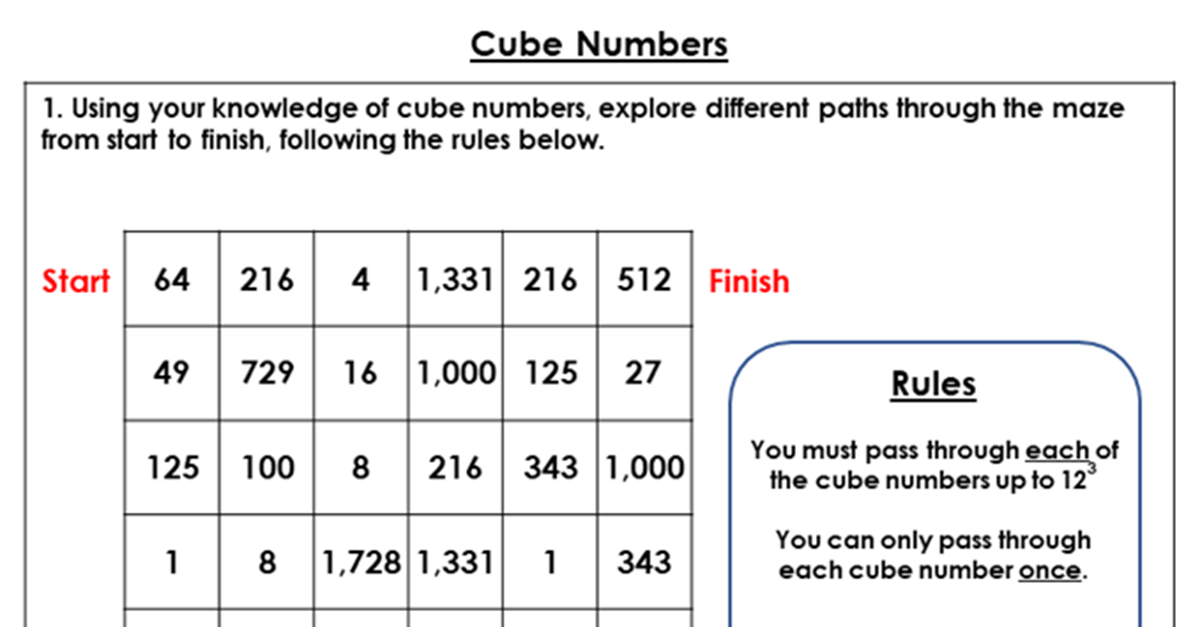
Discussion Problem

This worksheet includes two discussion problems which can be used in pairs or small groups to further pupils' understanding of the concepts taught in this lesson.

This Year 5 Cube Numbers Maths Challenge checks pupils’ understanding of cube numbers while also aiming to develop their problem solving abilities.

This differentiated worksheet includes varied fluency and reasoning and problem solving questions to support the teaching of this step.

2 Additional Activities

Learning Video Clip

The organisers of the Olympic Games have lost some medals and need to order some more. Use your knowledge of cube numbers to help them work out how many they need to order and how many spectators can fit in the stands.

Consolidation Pack

This resource is aimed at Year 5 Expected and has been designed to give children the opportunity to consolidate the skills they have learned in Autumn Block 4 – Number: Multiplication and Division.

Home Learning Pack

This Autumn week 10 Maths pack contains varied fluency, reasoning and problem solving worksheets.

D Download Packs

Stay in touch.

01422 419608

[email protected]

Interested in getting weekly updates from us? Then sign up to our newsletter here!

Information

• Cookie Policy
• Privacy Policy
• Terms and Conditions

Copyright: Classroom Secrets 2024

Company number: 8401067

VAT number: 248 8245 74

• Terms & Conditions

Designed by Classroom Secrets

Cube Numbers Questions

Primary Study Cards

• 5-a-day Answers
• Worksheet Answers

Cube Numbers

Cube numbers are special numbers that you get when you multiply a number by itself twice. It’s like taking a number and using it three times in a multiplication. For example, if we think about building a cube out of blocks, the total number of blocks used gives us a cube number. This concept is not only fun but also very useful, especially when we talk about shapes and spaces in geometry.

What are Cube Numbers?

• 2³ = 2 × 2 × 2 = 8
• 3³ = 3 × 3 × 3 = 27
• 4³ = 4 × 4 × 4 = 64
• 5³ = 5 × 5 × 5 = 125

In geometry, to find out how much space is inside a cube, you multiply the side lengths together. But since all sides of a cube are the same, you just take the length of one side and multiply it by itself three times. This is written as a 3, where a is the side length. So, the space inside a cube is a special kind of number called a cube number.

How to Cube a Number?

ubing a number means multiplying that number by itself twice. It’s a simple process that involves taking any given number and using it in a multiplication equation three times. Here’s how you do it:

• Pick a Number : Start with any number you want to cube. Let’s say you choose the number 4.
• Multiply It by Itself : Take that number and multiply it by itself: 4 x 4 = 16.
• Multiply One More Time : Now, take the result and multiply it by the original number again: 16 x 4 = 64.

So, when you cube the number 4, you get 64. This is represented mathematically as 4³ or 4×4×4 =64.

To cube a number is to use it in a multiplication three times, leading to results like 2³ or 2×2×2 =8 and 3³ or 3×3×3 =27. It’s a handy math tool, especially in geometry and when working with volumes.

Cube of a Fraction

Cubing a fraction involves raising it to the power of three, just like you would cube a whole number. This process multiplies the fraction by itself twice more, affecting both the numerator (the top number) and the denominator (the bottom number). The result is a new fraction that represents the original fraction cubed. Here’s how it works in detail:

Steps to Cube a Fraction

• Identify the Fraction : Start with your fraction, which has a numerator and a denominator, like ½.
• Multiply the Numerator by Itself Three Times : Take the numerator and multiply it by itself twice more. For example, if your fraction is ½, multiply 1 (numerator) by itself three times (1 x 1 x 1), which equals 1.
• Multiply the Denominator by Itself Three Times : Similarly, take the denominator and multiply it by itself twice more. Using ½ as an example, multiply 2 (denominator) by itself three times (2 x 2 x 2), which equals 8.
• Combine the Results : The result of the numerator’s multiplication becomes the new numerator, and the result of the denominator’s multiplication becomes the new denominator. Therefore, cubing ½ results in 1/8.

Let’s cube the fraction ¾.

• Cubing the numerator: 3 x 3 x 3 = 27.
• Cubing the denominator: 4 x 4 x 4 = 64.
• Combining the results gives you the fraction 27/64, which is the cube of ¾.

Cube of Negative Numbers

Cubing a negative number means multiplying the negative number by itself three times. When you do this with a negative number, the result is always a negative number. This happens because multiplying two negative numbers together gives you a positive result, but then multiplying that positive result by another negative number turns it back into a negative.

How It Works

• First Step : Multiply the negative number by itself once. (-n) × (-n) = positive result.
• Second Step : Multiply that positive result by the negative number again. Positive result × (-n) = negative result.

Let’s cube -3:

• First, -3 × -3 = 9 (since a negative times a negative gives a positive).
• Then, 9 × -3 = -27.

So, the cube of -3 is -27.

Cube Numbers List From 1 to 50

Why are they called cube numbers?

Cube numbers get their name because they help us figure out how much space is inside a 3D shape called a cube, where all sides are the same size. To find a cube’s volume, you multiply the length of one side by itself twice, which is also known as “cubing.”

Since all sides of a cube are equal, finding the volume is easy – just cube the length of one side!

For instance, if a cube’s side is 2 inches long, its volume is 8 cubic inches (because 2 x 2 x 2 = 8). Similarly, if a cube’s volume is 27 cubic inches, each side is 3 inches long (since 3 x 3 x 3 = 27).

Imagine pictures that show these examples of cube numbers to understand better.

When do children learn about cube numbers in elementary school?

• Cube numbers are usually introduced to students in 4th to 5th grade.
• The concept helps students understand the process of multiplying a number by itself twice, which is essential for grasping volume concepts.
• The exact timing of introduction can vary depending on the curriculum and the educational approach adopted by schools or regions.
• Learning cube numbers enhances spatial awareness, as students learn about volume and geometry.
• It also improves numerical fluency, as students practice computing and recognizing cube numbers.
• Introducing cube numbers prepares students for algebra, familiarizing them with the concept of numbers raised to powers.
• Students develop problem-solving skills by applying the concept of cubing to mathematical and real-world problems.

How do cube numbers relate to other areas of math?

Cube numbers, or cubed numbers, are an integral part of mathematical learning, offering a foundational understanding that connects to various areas of mathematics. By delving into how cube numbers relate to other areas, students can appreciate the interconnectedness of mathematical concepts and enhance their problem-solving skills.

Cube numbers play a crucial role in algebra, especially in understanding polynomials and equations. They help in the comprehension of exponentiation, where numbers are raised to powers, a fundamental concept in algebraic expressions and functions. For example, solving cubic equations, which include terms raised to the third power, directly involves cube numbers. This knowledge is also pivotal in exploring patterns and sequences, including geometric sequences where each term is a certain multiple of the previous one.

In geometry, cube numbers are essential in calculating the volume of cubic shapes. Understanding the volume of a cube, where all sides are equal, directly applies the concept of cubing a number. This extends to more complex geometric problems involving cuboids or other three-dimensional shapes where dimensions are multiplied to find volume, reinforcing spatial reasoning and the practical application of cube numbers.

Number Theory

Cube numbers intersect with number theory in the study of perfect cubes and their properties. Investigating patterns within cube numbers, such as the sum of consecutive odd numbers forming a cube, enriches students’ understanding of number properties and relationships. Furthermore, number theory explores the uniqueness of cube numbers, including problems related to Fermat’s Last Theorem, which involves cubes among other powers.

In calculus, cube numbers find their application in understanding the behavior of functions, especially when dealing with cubic functions. Derivatives and integrals involving cubic functions or powers demonstrate how changes in volume can be modeled and analyzed, providing a real-world application of cube numbers in measuring rates of change and accumulation.

Probability and Statistics

Cube numbers can also be seen in probability and statistics, albeit indirectly. For example, when calculating the volume of spaces or understanding geometric probabilities, cube numbers and their principles may be applied. They also appear in statistical formulas that involve cubic computations or models that describe three-dimensional space.

Real-World Applications

Beyond the classroom, cube numbers are utilized in various real-world contexts, such as physics, engineering, and computer science. For instance, in physics, understanding the concept of density involves cubing units of length to calculate volume, which is then used to determine the mass of an object per unit volume. In computer science, algorithms that involve three-dimensional data processing may use cube numbers to optimize computations related to volume or spatial configurations.

Cube Numbers vs. Square Numbers

AI Generator

Text prompt

• Instructive
• Professional

10 Examples of Public speaking

20 Examples of Gas lighting

Cube Numbers - PowerPoint

Cube numbers are an essential concept in mathematics, particularly for Year 5 students learning about multiplication and division. A cube number is the product you get when you multiply a number by itself three times. For example, when you multiply 2 by itself twice more (2 x 2 x 2), you get 8, which is a cube number. This concept is visually represented by the volume of cubes, where the number of units along each edge of the cube is the same. To express a number as cubed in mathematical notation, a small '3' is placed to the top right of the number, such as 4 cubed being written as 4³.

The educational resources include engaging activities where students can use multilink cubes to explore and verify cube numbers. They are encouraged to identify cube numbers from visual representations and to calculate the cube of different numbers, such as 3³ equalling 27. Additionally, worksheets provide exercises for matching numbers to their equivalent cube values, solving equations involving cube numbers, and identifying cube numbers from a list. These exercises are designed to enhance fluency, reasoning, and problem-solving skills related to cube numbers, with answers provided to facilitate learning and self-assessment.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Recognise and use square numbers and cube numbers year 5

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

7 October 2018

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Fluency, reasoning & problem solving

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Thank you - lots of ideas for problem solving.

Empty reply does not make any sense for the end user

Very useful, saved me so much time. Thanks.

Excellent resource. Worked well with a challenging Y10 set.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: