hypothesis test z statistic

Z-test Calculator

Table of contents

This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean . Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. You can also choose whether the calculator should determine the p-value from Z-test or you'd rather use the critical value approach!

Read on to learn more about Z-test in statistics, and, in particular, when to use Z-tests, what is the Z-test formula, and whether to use Z-test vs. t-test. As a bonus, we give some step-by-step examples of how to perform Z-tests!

Or you may also check our t-statistic calculator , where you can learn the concept of another essential statistic. If you are also interested in F-test, check our F-statistic calculator .

What is a Z-test?

A one sample Z-test is one of the most popular location tests. The null hypothesis is that the population mean value is equal to a given number, μ 0 \mu_0 μ 0 ​ :

We perform a two-tailed Z-test if we want to test whether the population mean is not μ 0 \mu_0 μ 0 ​ :

and a one-tailed Z-test if we want to test whether the population mean is less/greater than μ 0 \mu_0 μ 0 ​ :

Let us now discuss the assumptions of a one-sample Z-test.

When do I use Z-tests?

You may use a Z-test if your sample consists of independent data points and:

the data is normally distributed , and you know the population variance ;

the sample is large , and data follows a distribution which has a finite mean and variance. You don't need to know the population variance.

The reason these two possibilities exist is that we want the test statistics that follow the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the former case, it is an exact standard normal distribution, while in the latter, it is approximately so, thanks to the central limit theorem.

The question remains, "When is my sample considered large?" Well, there's no universal criterion. In general, the more data points you have, the better the approximation works. Statistics textbooks recommend having no fewer than 50 data points, while 30 is considered the bare minimum.

Z-test formula

Let x 1 , . . . , x n x_1, ..., x_n x 1 ​ , ... , x n ​ be an independent sample following the normal distribution N ( μ , σ 2 ) \mathrm N(\mu, \sigma^2) N ( μ , σ 2 ) , i.e., with a mean equal to μ \mu μ , and variance equal to σ 2 \sigma ^2 σ 2 .

We pose the null hypothesis, H 0  ⁣  ⁣ :  ⁣  ⁣   μ = μ 0 \mathrm H_0 \!\!:\!\! \mu = \mu_0 H 0 ​ :   μ = μ 0 ​ .

We define the test statistic, Z , as:

x ˉ \bar x x ˉ is the sample mean, i.e., x ˉ = ( x 1 + . . . + x n ) / n \bar x = (x_1 + ... + x_n) / n x ˉ = ( x 1 ​ + ... + x n ​ ) / n ;

μ 0 \mu_0 μ 0 ​ is the mean postulated in H 0 \mathrm H_0 H 0 ​ ;

n n n is sample size; and

σ \sigma σ is the population standard deviation.

In what follows, the uppercase Z Z Z stands for the test statistic (treated as a random variable), while the lowercase z z z will denote an actual value of Z Z Z , computed for a given sample drawn from N(μ,σ²).

If H 0 \mathrm H_0 H 0 ​ holds, then the sum S n = x 1 + . . . + x n S_n = x_1 + ... + x_n S n ​ = x 1 ​ + ... + x n ​ follows the normal distribution, with mean n μ 0 n \mu_0 n μ 0 ​ and variance n 2 σ n^2 \sigma n 2 σ . As Z Z Z is the standardization (z-score) of S n / n S_n/n S n ​ / n , we can conclude that the test statistic Z Z Z follows the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , provided that H 0 \mathrm H_0 H 0 ​ is true. By the way, we have the z-score calculator if you want to focus on this value alone.

If our data does not follow a normal distribution, or if the population standard deviation is unknown (and thus in the formula for Z Z Z we substitute the population standard deviation σ \sigma σ with sample standard deviation), then the test statistics Z Z Z is not necessarily normal. However, if the sample is sufficiently large, then the central limit theorem guarantees that Z Z Z is approximately N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

In the sections below, we will explain to you how to use the value of the test statistic, z z z , to make a decision , whether or not you should reject the null hypothesis . Two approaches can be used in order to arrive at that decision: the p-value approach, and critical value approach - and we cover both of them! Which one should you use? In the past, the critical value approach was more popular because it was difficult to calculate p-value from Z-test. However, with help of modern computers, we can do it fairly easily, and with decent precision. In general, you are strongly advised to report the p-value of your tests!

p-value from Z-test

Formally, the p-value is the smallest level of significance at which the null hypothesis could be rejected. More intuitively, p-value answers the questions: provided that I live in a world where the null hypothesis holds, how probable is it that the value of the test statistic will be at least as extreme as the z z z - value I've got for my sample? Hence, a small p-value means that your result is very improbable under the null hypothesis, and so there is strong evidence against the null hypothesis - the smaller the p-value, the stronger the evidence.

To find the p-value, you have to calculate the probability that the test statistic, Z Z Z , is at least as extreme as the value we've actually observed, z z z , provided that the null hypothesis is true. (The probability of an event calculated under the assumption that H 0 \mathrm H_0 H 0 ​ is true will be denoted as P r ( event ∣ H 0 ) \small \mathrm{Pr}(\text{event} | \mathrm{H_0}) Pr ( event ∣ H 0 ​ ) .) It is the alternative hypothesis which determines what more extreme means :

• Two-tailed Z-test: extreme values are those whose absolute value exceeds ∣ z ∣ |z| ∣ z ∣ , so those smaller than − ∣ z ∣ -|z| − ∣ z ∣ or greater than ∣ z ∣ |z| ∣ z ∣ . Therefore, we have:

The symmetry of the normal distribution gives:

• Left-tailed Z-test: extreme values are those smaller than z z z , so
• Right-tailed Z-test: extreme values are those greater than z z z , so

To compute these probabilities, we can use the cumulative distribution function, (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , which for a real number, x x x , is defined as:

Also, p-values can be nicely depicted as the area under the probability density function (pdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , due to:

Two-tailed Z-test and one-tailed Z-test

With all the knowledge you've got from the previous section, you're ready to learn about Z-tests.

• Two-tailed Z-test:

From the fact that Φ ( − z ) = 1 − Φ ( z ) \Phi(-z) = 1 - \Phi(z) Φ ( − z ) = 1 − Φ ( z ) , we deduce that

The p-value is the area under the probability distribution function (pdf) both to the left of − ∣ z ∣ -|z| − ∣ z ∣ , and to the right of ∣ z ∣ |z| ∣ z ∣ :

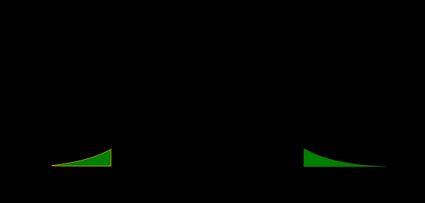
• Left-tailed Z-test:

The p-value is the area under the pdf to the left of our z z z :

• Right-tailed Z-test:

The p-value is the area under the pdf to the right of z z z :

The decision as to whether or not you should reject the null hypothesis can be now made at any significance level, α \alpha α , you desire!

if the p-value is less than, or equal to, α \alpha α , the null hypothesis is rejected at this significance level; and

if the p-value is greater than α \alpha α , then there is not enough evidence to reject the null hypothesis at this significance level.

Z-test critical values & critical regions

The critical value approach involves comparing the value of the test statistic obtained for our sample, z z z , to the so-called critical values . These values constitute the boundaries of regions where the test statistic is highly improbable to lie . Those regions are often referred to as the critical regions , or rejection regions . The decision of whether or not you should reject the null hypothesis is then based on whether or not our z z z belongs to the critical region.

The critical regions depend on a significance level, α \alpha α , of the test, and on the alternative hypothesis. The choice of α \alpha α is arbitrary; in practice, the values of 0.1, 0.05, or 0.01 are most commonly used as α \alpha α .

Once we agree on the value of α \alpha α , we can easily determine the critical regions of the Z-test:

To decide the fate of H 0 \mathrm H_0 H 0 ​ , check whether or not your z z z falls in the critical region:

If yes, then reject H 0 \mathrm H_0 H 0 ​ and accept H 1 \mathrm H_1 H 1 ​ ; and

If no, then there is not enough evidence to reject H 0 \mathrm H_0 H 0 ​ .

As you see, the formulae for the critical values of Z-tests involve the inverse, Φ − 1 \Phi^{-1} Φ − 1 , of the cumulative distribution function (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

How to use the one-sample Z-test calculator?

Our calculator reduces all the complicated steps:

Choose the alternative hypothesis: two-tailed or left/right-tailed.

In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α \alpha α .

Enter the value of the test statistic, z z z . If you don't know it, then you can enter some data that will allow us to calculate your z z z for you:

• sample mean x ˉ \bar x x ˉ (If you have raw data, go to the average calculator to determine the mean);
• tested mean μ 0 \mu_0 μ 0 ​ ;
• sample size n n n ; and
• population standard deviation σ \sigma σ (or sample standard deviation if your sample is large).

Results appear immediately below the calculator.

If you want to find z z z based on p-value , please remember that in the case of two-tailed tests there are two possible values of z z z : one positive and one negative, and they are opposite numbers. This Z-test calculator returns the positive value in such a case. In order to find the other possible value of z z z for a given p-value, just take the number opposite to the value of z z z displayed by the calculator.

Z-test examples

To make sure that you've fully understood the essence of Z-test, let's go through some examples:

• A bottle filling machine follows a normal distribution. Its standard deviation, as declared by the manufacturer, is equal to 30 ml. A juice seller claims that the volume poured in each bottle is, on average, one liter, i.e., 1000 ml, but we suspect that in fact the average volume is smaller than that...

Formally, the hypotheses that we set are the following:

H 0  ⁣ :   μ = 1000  ml \mathrm H_0 \! : \mu = 1000 \text{ ml} H 0 ​ :   μ = 1000  ml

H 1  ⁣ :   μ < 1000  ml \mathrm H_1 \! : \mu \lt 1000 \text{ ml} H 1 ​ :   μ < 1000  ml

We went to a shop and bought a sample of 9 bottles. After carefully measuring the volume of juice in each bottle, we've obtained the following sample (in milliliters):

1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 \small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 .

Sample size: n = 9 n = 9 n = 9 ;

Sample mean: x ˉ = 980   m l \bar x = 980 \ \mathrm{ml} x ˉ = 980   ml ;

Population standard deviation: σ = 30   m l \sigma = 30 \ \mathrm{ml} σ = 30   ml ;

And, therefore, p-value = Φ ( − 2 ) ≈ 0.0228 \text{p-value} = \Phi(-2) \approx 0.0228 p-value = Φ ( − 2 ) ≈ 0.0228 .

As 0.0228 < 0.05 0.0228 \lt 0.05 0.0228 < 0.05 , we conclude that our suspicions aren't groundless; at the most common significance level, 0.05, we would reject the producer's claim, H 0 \mathrm H_0 H 0 ​ , and accept the alternative hypothesis, H 1 \mathrm H_1 H 1 ​ .

We tossed a coin 50 times. We got 20 tails and 30 heads. Is there sufficient evidence to claim that the coin is biased?

Clearly, our data follows Bernoulli distribution, with some success probability p p p and variance σ 2 = p ( 1 − p ) \sigma^2 = p (1-p) σ 2 = p ( 1 − p ) . However, the sample is large, so we can safely perform a Z-test. We adopt the convention that getting tails is a success.

Let us state the null and alternative hypotheses:

H 0  ⁣ :   p = 0.5 \mathrm H_0 \! : p = 0.5 H 0 ​ :   p = 0.5 (the coin is fair - the probability of tails is 0.5 0.5 0.5 )

H 1  ⁣ :   p ≠ 0.5 \mathrm H_1 \! : p \ne 0.5 H 1 ​ :   p  = 0.5 (the coin is biased - the probability of tails differs from 0.5 0.5 0.5 )

In our sample we have 20 successes (denoted by ones) and 30 failures (denoted by zeros), so:

Sample size n = 50 n = 50 n = 50 ;

Sample mean x ˉ = 20 / 50 = 0.4 \bar x = 20/50 = 0.4 x ˉ = 20/50 = 0.4 ;

Population standard deviation is given by σ = 0.5 × 0.5 \sigma = \sqrt{0.5 \times 0.5} σ = 0.5 × 0.5 ​ (because 0.5 0.5 0.5 is the proportion p p p hypothesized in H 0 \mathrm H_0 H 0 ​ ). Hence, σ = 0.5 \sigma = 0.5 σ = 0.5 ;

• And, therefore

Since 0.1573 > 0.1 0.1573 \gt 0.1 0.1573 > 0.1 we don't have enough evidence to reject the claim that the coin is fair , even at such a large significance level as 0.1 0.1 0.1 . In that case, you may safely toss it to your Witcher or use the coin flip probability calculator to find your chances of getting, e.g., 10 heads in a row (which are extremely low!).

What is the difference between Z-test vs t-test?

We use a t-test for testing the population mean of a normally distributed dataset which had an unknown population standard deviation . We get this by replacing the population standard deviation in the Z-test statistic formula by the sample standard deviation, which means that this new test statistic follows (provided that H₀ holds) the t-Student distribution with n-1 degrees of freedom instead of N(0,1) .

When should I use t-test over the Z-test?

For large samples, the t-Student distribution with n degrees of freedom approaches the N(0,1). Hence, as long as there are a sufficient number of data points (at least 30), it does not really matter whether you use the Z-test or the t-test, since the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test instead of Z-test .

How do I calculate the Z test statistic?

To calculate the Z test statistic:

• Compute the arithmetic mean of your sample .
• From this mean subtract the mean postulated in null hypothesis .
• Multiply by the square root of size sample .
• Divide by the population standard deviation .
• That's it, you've just computed the Z test statistic!

Here, we perform a Z-test for population mean μ. Null hypothesis H₀: μ = μ₀.

Alternative hypothesis H₁

Significance level α

The probability that we reject the true hypothesis H₀ (type I error).

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers

Z-test : Formula, Types, Examples

Z-test is especially useful when you have a large sample size and know the population’s standard deviation. Different tests are used in statistics to compare distinct samples or groups and make conclusions about populations. These tests, also referred to as statistical tests, concentrate on examining the probability or possibility of acquiring the observed data under particular premises or hypotheses. They offer a framework for evaluating the evidence for or against a given hypothesis.

Table of Content

What is Z-Test?

Z-test formula, when to use z-test, hypothesis testing, steps to perform z-test, type of z-test, practice problems.

Z-test is a statistical test that is used to determine whether the mean of a sample is significantly different from a known population mean when the population standard deviation is known. It is particularly useful when the sample size is large (>30).

Z-test can also be defined as a statistical method that is used to determine whether the distribution of the test statistics can be approximated using the normal distribution or not. It is the method to determine whether two sample means are approximately the same or different when their variance is known and the sample size is large (should be >= 30).

The Z-test compares the difference between the sample mean and the population means by considering the standard deviation of the sampling distribution. The resulting Z-score represents the number of standard deviations that the sample mean deviates from the population mean. This Z-Score is also known as Z-Statistics, and can be formulated as:

[Tex]\text{Z-Score} = \frac{\bar{x}-\mu}{\sigma} [/Tex]

• [Tex]\bar{x}  [/Tex] : mean of the sample.
• [Tex]\mu  [/Tex] : mean of the population.
• [Tex]\sigma  [/Tex] : Standard deviation of the population.

z-test assumes that the test statistic (z-score) follows a standard normal distribution.

The average family annual income in India is 200k, with a standard deviation of 5k, and the average family annual income in Delhi is 300k.

Then Z-Score for Delhi will be.

[Tex]\begin{aligned} \text{Z-Score}&=\frac{\bar{x}-\mu}{\sigma} \\&=\frac{300-200}{5} \\&=20 \end{aligned} [/Tex]

This indicates that the average family’s annual income in Delhi is 20 standard deviations above the mean of the population (India).

• The sample size should be greater than 30. Otherwise, we should use the t-test.
• Samples should be drawn at random from the population.
• The standard deviation of the population should be known.
• Samples that are drawn from the population should be independent of each other.
• The data should be normally distributed , however, for a large sample size, it is assumed to have a normal distribution because central limit theorem

A hypothesis is an educated guess/claim about a particular property of an object. Hypothesis testing is a way to validate the claim of an experiment.

• Null Hypothesis: The null hypothesis is a statement that the value of a population parameter (such as proportion, mean, or standard deviation) is equal to some claimed value. We either reject or fail to reject the null hypothesis. The null hypothesis is denoted by H 0 .
• Alternate Hypothesis: The alternative hypothesis is the statement that the parameter has a value that is different from the claimed value. It is denoted by H A .
• Level of significance: It means the degree of significance in which we accept or reject the null hypothesis. Since in most of the experiments 100% accuracy is not possible for accepting or rejecting a hypothesis, we, therefore, select a level of significance. It is denoted by alpha (∝).
• First, identify the null and alternate hypotheses.
• Determine the level of significance (∝).
• Find the critical value of z in the z-test using
• n: sample size.
• Now compare with the hypothesis and decide whether to reject or not reject the null hypothesis

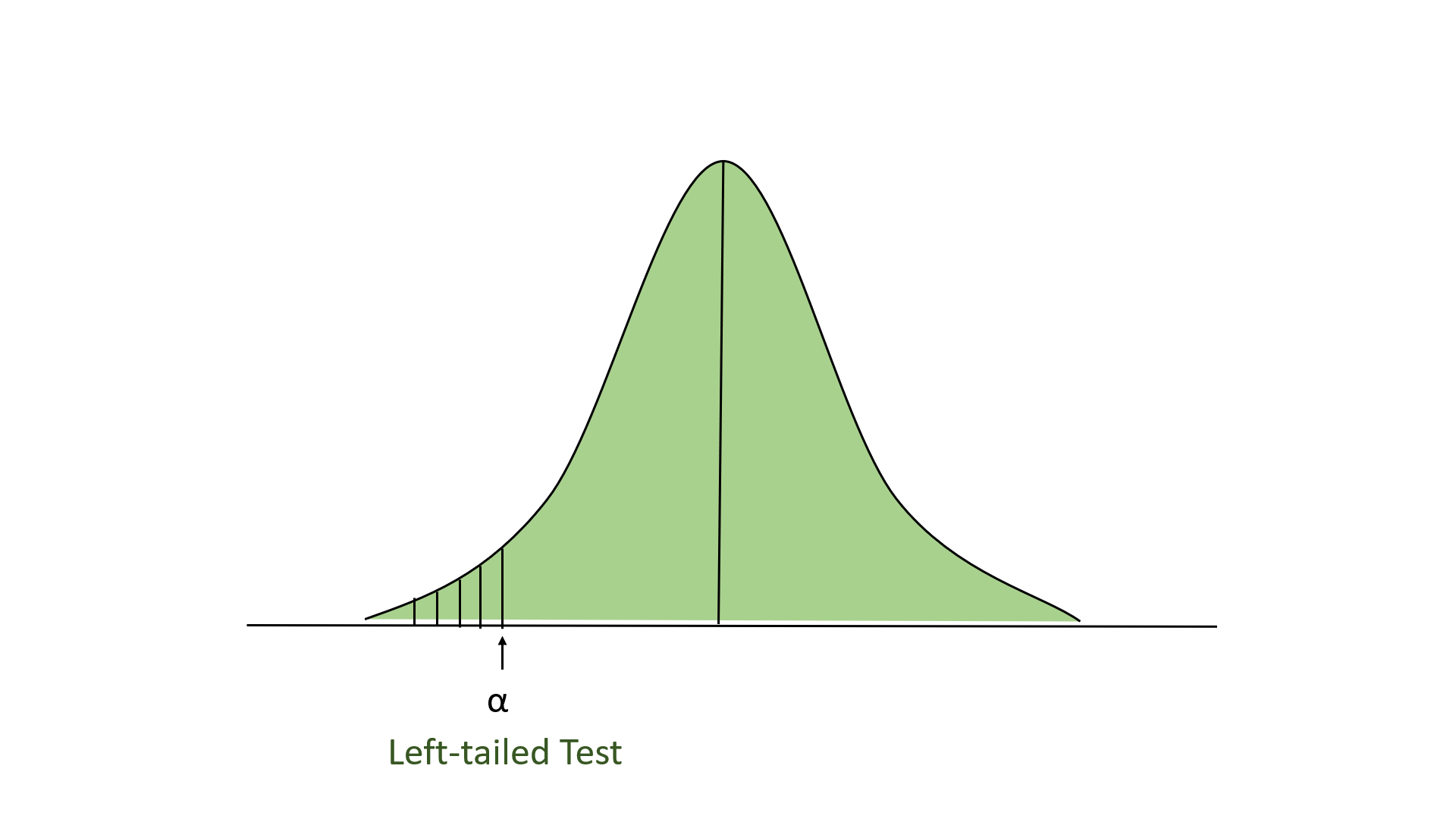
Left-tailed Test

In this test, our region of rejection is located to the extreme left of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.

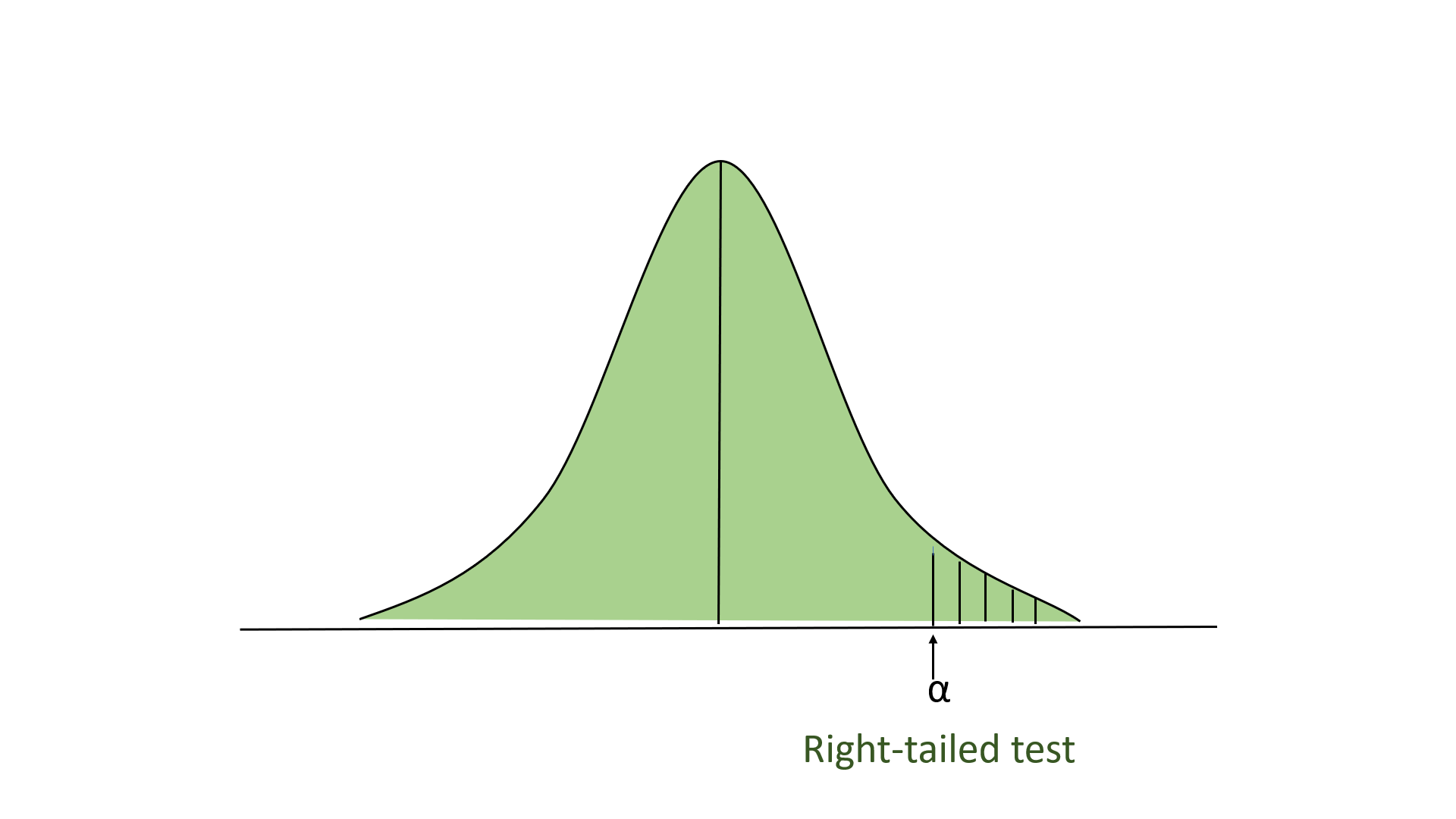
Right-tailed Test

In this test, our region of rejection is located to the extreme right of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.

One-Tailed Test

 A school claimed that the students who study that are more intelligent than the average school. On calculating the IQ scores of 50 students, the average turns out to be 110. The mean of the population IQ is 100 and the standard deviation is 15. State whether the claim of the principal is right or not at a 5% significance level.

• First, we define the null hypothesis and the alternate hypothesis. Our null hypothesis will be: [Tex]H_0 : \mu  = 100        [/Tex] and our alternate hypothesis. [Tex]H_A : \mu > 100 [/Tex]
• State the level of significance. Here, our level of significance is given in this question ( [Tex]\alpha [/Tex]  =0.05), if not given then we take ∝=0.05 in general.
• Now, we compute the Z-Score: X = 110 Mean = 100 Standard Deviation = 15 Number of samples = 50 [Tex]\begin{aligned} \text{Z-Score}&=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \\&=\frac{110-100}{15/\sqrt{50}} \\&=\frac{10}{2.12} \\&=4.71 \end{aligned} [/Tex]
• Now, we look up to the z-table. For the value of ∝=0.05, the z-score for the right-tailed test is 1.645.
• Here 4.71 >1.645, so we reject the null hypothesis. 
• If the z-test statistics are less than the z-score, then we will not reject the null hypothesis.

Code Implementations of One-Tailed Z-Test

Z-Score : 4.714045207910317Critical Z-Score : 1.6448536269514722Reject Null Hypothesisp-value : 1.2142337364462463e-06Reject Null Hypothesis

Two-tailed test

In this test, our region of rejection is located to both extremes of the distribution. Here our null hypothesis is that the claimed value is equal to the mean population value.

Below is an example of performing the z-test:

Two-sampled z-test

In this test, we have provided 2 normally distributed and independent populations, and we have drawn samples at random from both populations. Here, we consider u 1 and u 2 to be the population mean, and X 1 and X 2 to be the observed sample mean. Here, our null hypothesis could be like this:

[Tex]H_{0} : \mu_{1} -\mu_{2} = 0    [/Tex]

and alternative hypothesis

[Tex]H_{1} :  \mu_{1} – \mu_{2} \ne 0    [/Tex]

and the formula for calculating the z-test score:

[Tex]Z = \frac{\left ( \overline{X_{1}} – \overline{X_{2}} \right ) – \left ( \mu_{1} – \mu_{2} \right )}{\sqrt{\frac{\sigma_{1}^2}{n_{1}} + \frac{\sigma_{2}^2}{n_{2}}}}    [/Tex]

where  [Tex]\sigma_1 [/Tex]   and  [Tex]\sigma_2 [/Tex]   are the standard deviation and n 1 and n 2 are the sample size of population corresponding to u 1 and u 2 .  

There are two groups of students preparing for a competition: Group A and Group B. Group A has studied offline classes, while Group B has studied online classes. After the examination, the score of each student comes. Now we want to determine whether the online or offline classes are better.

Group A: Sample size = 50, Sample mean = 75, Sample standard deviation = 10 Group B: Sample size = 60, Sample mean = 80, Sample standard deviation = 12

Assuming a 5% significance level, perform a two-sample z-test to determine if there is a significant difference between the online and offline classes.

Step 1: Null & Alternate Hypothesis

• Null Hypothesis: There is no significant difference between the mean score between the online and offline classes [Tex] \mu_1 -\mu_2 = 0 [/Tex]
• Alternate Hypothesis: There is a significant difference in the mean scores between the online and offline classes. [Tex] \mu_1 -\mu_2 \neq 0 [/Tex]

Step 2: Significance Label

• Significance Label: 5%  [Tex]\alpha = 0.05 [/Tex]

Step 3: Z-Score

[Tex]\begin{aligned} \text{Z-score} &= \frac{(x_1-x_2)-(\mu_1 -\mu_2)} {\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_1}}} \\ &= \frac{(75-80)-0} {\sqrt{\frac{10^2}{50}+\frac{12^2}{60}}} \\ &= \frac{-5} {\sqrt{2+2.4}} \\ &= \frac{-5} {2.0976} \\&=-2.384 \end{aligned} [/Tex]

Step 4: Check to Critical Z-Score value in the Z-Table for apha/2 = 0.025

•  Critical Z-Score = 1.96

Step 5: Compare with the absolute Z-Score value

• absolute(Z-Score) > Critical Z-Score
• Reject the null hypothesis. There is a significant difference between the online and offline classes.

Code Implementations on Two-sampled Z-test

Z-Score: 2.3836564731139807 Critical Z-Score: 1.959963984540054 Reject the null hypothesis. There is a significant difference between the online and offline classes. P-Value : 0.01714159544079563 Reject the null hypothesis. There is a significant difference between the online and offline classes.

Solved examples :

Example 1: One-sample Z-test

Problem: A company claims that the average battery life of their new smartphone is 12 hours. A consumer group tests 100 phones and finds the average battery life to be 11.8 hours with a population standard deviation of 0.5 hours. At a 5% significance level, is there evidence to refute the company’s claim?

Solution: Step 1: State the hypotheses H₀: μ = 12 (null hypothesis) H₁: μ ≠ 12 (alternative hypothesis) Step 2: Calculate the Z-score Z = (x̄ – μ) / (σ / √n) = (11.8 – 12) / (0.5 / √100) = -0.2 / 0.05 = -4 Step 3: Find the critical value (two-tailed test at 5% significance) Z₀.₀₂₅ = ±1.96 Step 4: Compare Z-score with critical value |-4| > 1.96, so we reject the null hypothesis. Conclusion: There is sufficient evidence to refute the company’s claim about battery life.

Problem: A researcher wants to compare the effectiveness of two different medications for reducing blood pressure. Medication A is tested on 50 patients, resulting in a mean reduction of 15 mmHg with a standard deviation of 3 mmHg. Medication B is tested on 60 patients, resulting in a mean reduction of 13 mmHg with a standard deviation of 4 mmHg. At a 1% significance level, is there a significant difference between the two medications?

Step 1: State the hypotheses H₀: μ₁ – μ₂ = 0 (null hypothesis) H₁: μ₁ – μ₂ ≠ 0 (alternative hypothesis) Step 2: Calculate the Z-score Z = (x̄₁ – x̄₂) / √((σ₁²/n₁) + (σ₂²/n₂)) = (15 – 13) / √((3²/50) + (4²/60)) = 2 / √(0.18 + 0.2667) = 2 / 0.6455 = 3.10 Step 3: Find the critical value (two-tailed test at 1% significance) Z₀.₀₀₅ = ±2.576 Step 4: Compare Z-score with critical value 3.10 > 2.576, so we reject the null hypothesis. Conclusion: There is a significant difference between the effectiveness of the two medications at the 1% significance level.

Problem 3 : A polling company claims that 60% of voters support a new policy. In a sample of 1000 voters, 570 support the policy. At a 5% significance level, is there evidence to support the company’s claim?

Step 1: State the hypotheses H₀: p = 0.60 (null hypothesis) H₁: p ≠ 0.60 (alternative hypothesis) Step 2: Calculate the Z-score p̂ = 570/1000 = 0.57 (sample proportion) Z = (p̂ – p) / √(p(1-p)/n) = (0.57 – 0.60) / √(0.60(1-0.60)/1000) = -0.03 / √(0.24/1000) = -0.03 / 0.0155 = -1.94 Step 3: Find the critical value (two-tailed test at 5% significance) Z₀.₀₂₅ = ±1.96 Step 4: Compare Z-score with critical value |-1.94| < 1.96, so we fail to reject the null hypothesis. Conclusion: There is not enough evidence to refute the polling company’s claim at the 5% significance level.

Problem 4 : A manufacturer claims that their light bulbs last an average of 1000 hours. A sample of 100 bulbs has a mean life of 985 hours. The population standard deviation is known to be 50 hours. At a 5% significance level, is there evidence to reject the manufacturer’s claim?

Solution: H₀: μ = 1000 H₁: μ ≠ 1000 Z = (x̄ – μ) / (σ / √n) = (985 – 1000) / (50 / √100) = -15 / 5 = -3 Critical value (α = 0.05, two-tailed): ±1.96 |-3| > 1.96, so reject H₀. Conclusion: There is sufficient evidence to reject the manufacturer’s claim at the 5% significance level.

Example 5 : Two factories produce semiconductors. Factory A’s chips have a mean resistance of 100 ohms with a standard deviation of 5 ohms. Factory B’s chips have a mean resistance of 98 ohms with a standard deviation of 4 ohms. Samples of 50 chips from each factory are tested. At a 1% significance level, is there a difference in mean resistance between the two factories?

H₀: μA – μB = 0 H₁: μA – μB ≠ 0 Z = (x̄A – x̄B) / √((σA²/nA) + (σB²/nB)) = (100 – 98) / √((5²/50) + (4²/50)) = 2 / √(0.5 + 0.32) = 2 / 0.872 = 2.29 Critical value (α = 0.01, two-tailed): ±2.576 |2.29| < 2.576, so fail to reject H₀. Conclusion: There is not enough evidence to conclude a difference in mean resistance at the 1% significance level.

Problem 6 : A political analyst claims that 40% of voters in a certain district support a new tax policy. In a random sample of 500 voters, 220 support the policy. At a 5% significance level, is there evidence to reject the analyst’s claim?

H₀: p = 0.40 H₁: p ≠ 0.40 p̂ = 220/500 = 0.44 Z = (p̂ – p) / √(p(1-p)/n) = (0.44 – 0.40) / √(0.40(1-0.40)/500) = 0.04 / 0.0219 = 1.83 Critical value (α = 0.05, two-tailed): ±1.96 |1.83| < 1.96, so fail to reject H₀. Conclusion: There is not enough evidence to reject the analyst’s claim at the 5% significance level.

Problem 7 : Two advertising methods are compared. Method A results in 150 sales out of 1000 contacts. Method B results in 180 sales out of 1200 contacts. At a 5% significance level, is there a difference in the effectiveness of the two methods?

H₀: pA – pB = 0 H₁: pA – pB ≠ 0 p̂A = 150/1000 = 0.15 p̂B = 180/1200 = 0.15 p̂ = (150 + 180) / (1000 + 1200) = 0.15 Z = (p̂A – p̂B) / √(p̂(1-p̂)(1/nA + 1/nB)) = (0.15 – 0.15) / √(0.15(1-0.15)(1/1000 + 1/1200)) = 0 / 0.0149 = 0 Critical value (α = 0.05, two-tailed): ±1.96 |0| < 1.96, so fail to reject H₀. Conclusion: There is no significant difference in the effectiveness of the two advertising methods at the 5% significance level.

Problem 8 : A new treatment for a disease is tested in two cities. In City A, 120 out of 400 patients recover. In City B, 140 out of 500 patients recover. At a 5% significance level, is there a difference in the recovery rates between the two cities?

H₀: pA – pB = 0 H₁: pA – pB ≠ 0 p̂A = 120/400 = 0.30 p̂B = 140/500 = 0.28 p̂ = (120 + 140) / (400 + 500) = 0.2889 Z = (p̂A – p̂B) / √(p̂(1-p̂)(1/nA + 1/nB)) = (0.30 – 0.28) / √(0.2889(1-0.2889)(1/400 + 1/500)) = 0.02 / 0.0316 = 0.633 Critical value (α = 0.05, two-tailed): ±1.96 |0.633| < 1.96, so fail to reject H₀. Conclusion: There is not enough evidence to conclude a difference in recovery rates between the two cities at the 5% significance level.

Problem 9 : Two advertising methods are compared. Method A results in 150 sales out of 1000 contacts. Method B results in 180 sales out of 1200 contacts. At a 5% significance level, is there a difference in the effectiveness of the two methods?

Problem 10 : A company claims that their product weighs 500 grams on average. A sample of 64 products has a mean weight of 498 grams. The population standard deviation is known to be 8 grams. At a 1% significance level, is there evidence to reject the company’s claim?

H₀: μ = 500 H₁: μ ≠ 500 Z = (x̄ – μ) / (σ / √n) = (498 – 500) / (8 / √64) = -2 / 1 = -2 Critical value (α = 0.01, two-tailed): ±2.576 |-2| < 2.576, so fail to reject H₀. Conclusion: There is not enough evidence to reject the company’s claim at the 1% significance level.

1).A cereal company claims that their boxes contain an average of 350 grams of cereal. A consumer group tests 100 boxes and finds a mean weight of 345 grams with a known population standard deviation of 15 grams. At a 5% significance level, is there evidence to refute the company’s claim?

2).A study compares the effect of two different diets on cholesterol levels. Diet A is tested on 50 people, resulting in a mean reduction of 25 mg/dL with a standard deviation of 8 mg/dL. Diet B is tested on 60 people, resulting in a mean reduction of 22 mg/dL with a standard deviation of 7 mg/dL. At a 1% significance level, is there a significant difference between the two diets?

3).A politician claims that 60% of voters in her district support her re-election. In a random sample of 1000 voters, 570 support her. At a 5% significance level, is there evidence to reject the politician’s claim?

4).Two different teaching methods are compared. Method A results in 80 students passing out of 120 students. Method B results in 90 students passing out of 150 students. At a 5% significance level, is there a difference in the effectiveness of the two methods?

5).A company claims that their new energy-saving light bulbs last an average of 10,000 hours. A sample of 64 bulbs has a mean life of 9,800 hours. The population standard deviation is known to be 500 hours. At a 1% significance level, is there evidence to reject the company’s claim?

6).The mean salary of employees in a large corporation is said to be $75,000 per year. A union representative suspects this is too high and surveys 100 randomly selected employees, finding a mean salary of $72,500. The population standard deviation is known to be $8,000. At a 5% significance level, is there evidence to support the union representative’s suspicion?

7).Two factories produce computer chips. Factory A’s chips have a mean processing speed of 3.2 GHz with a standard deviation of 0.2 GHz. Factory B’s chips have a mean processing speed of 3.3 GHz with a standard deviation of 0.25 GHz. Samples of 100 chips from each factory are tested. At a 5% significance level, is there a difference in mean processing speed between the two factories?

8).A new vaccine is claimed to be 90% effective. In a clinical trial with 500 participants, 440 develop immunity. At a 1% significance level, is there evidence to reject the claim about the vaccine’s effectiveness?

9).Two different advertising campaigns are tested. Campaign A results in 250 sales out of 2000 views. Campaign B results in 300 sales out of 2500 views. At a 5% significance level, is there a difference in the effectiveness of the two campaigns?

10).A quality control manager claims that the defect rate in a production line is 5%. In a sample of 1000 items, 65 are found to be defective. At a 5% significance level, is there evidence to suggest that the actual defect rate is different from the claimed 5%?

Type 1 error and Type II error

• Type I error: Type 1 error has occurred when we reject the null hypothesis, even when the hypothesis is true. This error is denoted by alpha.
• Type II error: Type II error occurred when we didn’t reject the null hypothesis, even when the hypothesis is false. This error is denoted by beta.

Z-tests are used to determine whether there is a statistically significant difference between a sample statistic and a population parameter, or between two population parameters.Z-tests are statistical tools used to determine if there’s a significant difference between a sample statistic and a population parameter, or between two population parameters. They’re applicable when dealing with large sample sizes (typically n > 30) and known population standard deviations. Z-tests can be used for analyzing means or proportions in both one-sample and two-sample scenarios. The process involves stating hypotheses, calculating a Z-score, comparing it to a critical value based on the chosen significance level (often 5% or 1%), and then making a decision to reject or fail to reject the null hypothesis.

What is the main limitation of the z-test?

The limitation of Z-Tests is that we don’t usually know the population standard deviation. What we do is: When we don’t know the population’s variability, we assume that the sample’s variability is a good basis for estimating the population’s variability.

What is the minimum sample for z-test?

A z-test can only be used if the population standard deviation is known and the sample size is 30 data points or larger. Otherwise, a t-test should be employed.

What is the application of z-test?

It is also used to determine if there is a significant difference between the mean of two independent samples. The z-test can also be used to compare the population proportion to an assumed proportion or to determine the difference between the population proportion of two samples.

What is the theory of the z-test?

The z test is a commonly used hypothesis test in inferential statistics that allows us to compare two populations using the mean values of samples from those populations, or to compare the mean of one population to a hypothesized value, when what we are interested in comparing is a continuous variable.

Similar Reads

• Engineering Mathematics
• Machine Learning
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Z-Test for Statistical Hypothesis Testing Explained

The Z-test is a statistical hypothesis test that determines where the distribution of the statistic we are measuring, like the mean, is part of the normal distribution.

The Z-test is a  statistical hypothesis test used to determine where the distribution of the test statistic we are measuring, like the  mean , is part of the  normal distribution .

While there are multiple types of Z-tests, we’ll focus on the easiest and most well-known one, the one-sample mean test. This is used to determine if the difference between the mean of a sample and the mean of a population is statistically significant.

What Is a Z-Test?

A Z-test determines whether there are any statistically significant differences between the means of two populations. A Z-test can only be applied if the standard deviation of each population is known and a sample size of at least 30 data points is available.

The name Z-test comes from the  Z-score of the normal distribution. This is a measure of how many standard deviations away a raw score or sample statistics is from the population’s mean. Z-tests are the most common statistical tests conducted in fields such as healthcare and  data science , making them essential to understand.

Requirements for a Z-Test

In order to conduct a Z-test, your statistics need to meet a few requirements:

• A sample size that’s greater than 30. This is because we want to ensure our sample mean comes from a distribution that is normal. As stated by the  central limit theorem , any distribution can be approximated as normally distributed if it contains more than 30 data points.
• The  standard deviation and mean of the population is known .
• The sample data is collected/acquired  randomly .

More on Data Science:   What Is Bootstrapping Statistics?

Z-Test Steps

There are four steps to complete a Z-test. Let’s examine each one: 

1. State the Null Hypothesis

The first step in a Z-test is to state the null hypothesis, H_0 . This is what you believe to be true from the population, which could be the mean of the population, μ_0 :

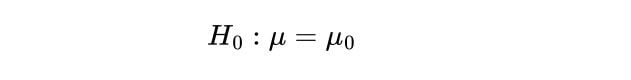
2. State the Alternate Hypothesis

Next, state the alternate hypothesis, H_1 . This is what you observe from your sample. If the sample mean is different from the population’s mean, then we say the mean is not equal to μ_0:

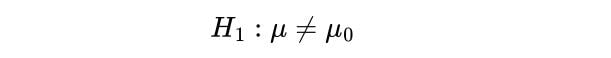
3. Choose Your Critical Value

Then, choose your critical value, α , which determines whether you accept or reject the null hypothesis. Typically, for a Z-test we would use a statistical significance of 5 percent which is  z = +/- 1.96  standard deviations from the population’s mean in the normal distribution:

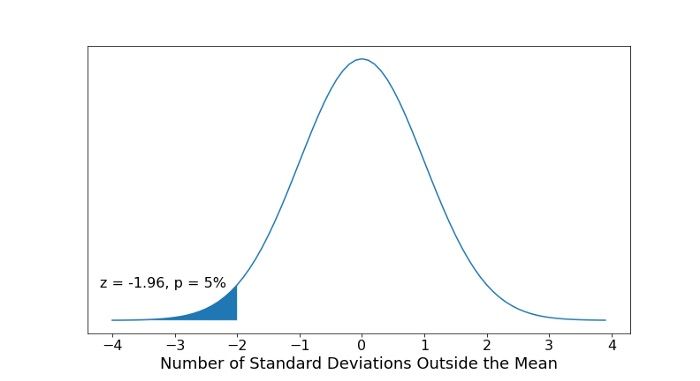
This critical value is based on confidence intervals . 

4. Calculate Your Z-Test Statistic

Compute the Z-test statistic using the sample mean, μ_1 , the population mean, μ_0 , the number of data points in the sample, n and the population’s standard deviation, σ :

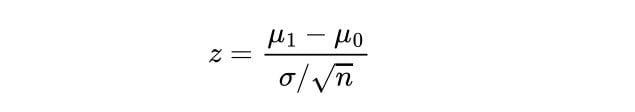
If the test statistic is greater (or lower depending on the test we are conducting) than the critical value, then the alternate hypothesis is true because the sample’s mean is  statistically significant enough from the population mean.

Another way to think about this is if the sample mean is so far away from the population mean, the alternate hypothesis has to be true or the sample is a complete anomaly .

More on Data Science: Basic Probability Theory and Statistics Terms to Know

Z-Test Example

Let’s go through an example to fully understand the one-sample mean Z-test.

A school says that its pupils are, on average, smarter than other schools. It takes a sample of 50 students whose average IQ measures to be 110. The population, or the rest of the schools, has an average IQ of 100 and standard deviation of 20. Is the school’s claim correct?

The null and alternate hypotheses are:

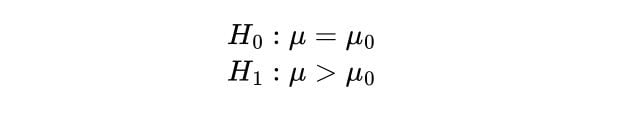
Where we are saying that our sample, the school, has a higher mean IQ than the population mean.

Now, this is what’s called a right-sided, one-tailed test as our sample mean is greater than the population’s mean. So, choosing a critical value of 5 percent, which equals a Z-score of 1.96 , we can only reject the null hypothesis if our Z-test statistic is greater than 1.96.

If the school claimed its students’ IQs were an average of 90, then we would use a left-tailed test, as shown in the figure above. We would then only reject the null hypothesis if our Z-test statistic is less than -1.96.

Computing our Z-test statistic, we see:

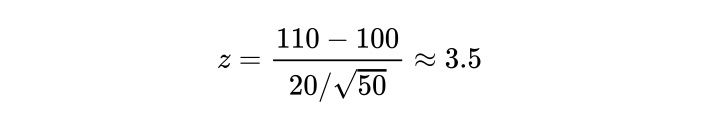
Therefore, we have sufficient evidence to reject the null hypothesis, and the school’s claim is right.

Types of Z-Tests

There are four main types of Z-tests to consider: 

One-Tailed Z-Test

A one-tailed Z-test involves an alternative hypothesis that claims the value of a parameter is either greater or less than what the null hypothesis claims it to be. This means the region of rejection falls to one side of the distribution, not both. A one-tailed Z-test can then be either left-tailed or right-tailed.

Left-Tailed Z-Test

A left-tailed Z-test involves an alternative hypothesis that claims the value of a parameter is less than what the null hypothesis claims it to be. In a normal distribution, the region of rejection would then be to the far left of the distribution’s center.

Right-Tailed Z-Test

A right-tailed Z-test involves an alternative hypothesis that claims the value of a parameter is greater than what the null hypothesis claims it to be. In a normal distribution, the region of rejection would then be to the far right of the distribution’s center.

Two-Tailed Z-Test

A two-tailed Z-test involves an alternative hypothesis that claims there is a significant difference between the means of two populations while the null hypothesis claims there is no significant difference. The alternative hypothesis doesn’t designate a direction since it merely includes a “not equal” sign, creating two regions of rejection that fall on either side of a distribution’s center. If results land in either region, the alternative hypothesis is accepted.

Frequently Asked Questions

What is a z-test used for.

A Z-test is used to determine whether there are any statistically significant differences in the means of two populations. Each population must have a known standard deviation and be large enough to provide a sample size of at least 30 data points.

When should you use a Z-test?

You should use a Z-test if you know a population’s standard deviation and can collect a sample size of at least 30 data points.

What is the difference of T-test and Z-test?

A T-test is used when the sample size is less than 30 data points and the population’s standard deviation is unknown. On the other hand, a Z-test is used when the sample size is at least 30 data points and the population’s standard deviation is known.

Recent Data Science Articles

Z test is a statistical test that is conducted on data that approximately follows a normal distribution. The z test can be performed on one sample, two samples, or on proportions for hypothesis testing. It checks if the means of two large samples are different or not when the population variance is known.

A z test can further be classified into left-tailed, right-tailed, and two-tailed hypothesis tests depending upon the parameters of the data. In this article, we will learn more about the z test, its formula, the z test statistic, and how to perform the test for different types of data using examples.

What is Z Test?

A z test is a test that is used to check if the means of two populations are different or not provided the data follows a normal distribution. For this purpose, the null hypothesis and the alternative hypothesis must be set up and the value of the z test statistic must be calculated. The decision criterion is based on the z critical value.

Z Test Definition

A z test is conducted on a population that follows a normal distribution with independent data points and has a sample size that is greater than or equal to 30. It is used to check whether the means of two populations are equal to each other when the population variance is known. The null hypothesis of a z test can be rejected if the z test statistic is statistically significant when compared with the critical value.

Z Test Formula

The z test formula compares the z statistic with the z critical value to test whether there is a difference in the means of two populations. In hypothesis testing , the z critical value divides the distribution graph into the acceptance and the rejection regions. If the test statistic falls in the rejection region then the null hypothesis can be rejected otherwise it cannot be rejected. The z test formula to set up the required hypothesis tests for a one sample and a two-sample z test are given below.

One-Sample Z Test

A one-sample z test is used to check if there is a difference between the sample mean and the population mean when the population standard deviation is known. The formula for the z test statistic is given as follows:

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the sample size.

The algorithm to set a one sample z test based on the z test statistic is given as follows:

Left Tailed Test:

Null Hypothesis: \(H_{0}\) : \(\mu = \mu_{0}\)

Alternate Hypothesis: \(H_{1}\) : \(\mu < \mu_{0}\)

Decision Criteria: If the z statistic < z critical value then reject the null hypothesis.

Right Tailed Test:

Alternate Hypothesis: \(H_{1}\) : \(\mu > \mu_{0}\)

Decision Criteria: If the z statistic > z critical value then reject the null hypothesis.

Two Tailed Test:

Alternate Hypothesis: \(H_{1}\) : \(\mu \neq \mu_{0}\)

Two Sample Z Test

A two sample z test is used to check if there is a difference between the means of two samples. The z test statistic formula is given as follows:

z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\). \(\overline{x_{1}}\), \(\mu_{1}\), \(\sigma_{1}^{2}\) are the sample mean, population mean and population variance respectively for the first sample. \(\overline{x_{2}}\), \(\mu_{2}\), \(\sigma_{2}^{2}\) are the sample mean, population mean and population variance respectively for the second sample.

The two-sample z test can be set up in the same way as the one-sample test. However, this test will be used to compare the means of the two samples. For example, the null hypothesis is given as \(H_{0}\) : \(\mu_{1} = \mu_{2}\).

Z Test for Proportions

A z test for proportions is used to check the difference in proportions. A z test can either be used for one proportion or two proportions. The formulas are given as follows.

One Proportion Z Test

A one proportion z test is used when there are two groups and compares the value of an observed proportion to a theoretical one. The z test statistic for a one proportion z test is given as follows:

z = \(\frac{p-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\). Here, p is the observed value of the proportion, \(p_{0}\) is the theoretical proportion value and n is the sample size.

The null hypothesis is that the two proportions are the same while the alternative hypothesis is that they are not the same.

Two Proportion Z Test

A two proportion z test is conducted on two proportions to check if they are the same or not. The test statistic formula is given as follows:

z =\(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\)

where p = \(\frac{x_{1}+x_{2}}{n_{1}+n_{2}}\)

\(p_{1}\) is the proportion of sample 1 with sample size \(n_{1}\) and \(x_{1}\) number of trials.

\(p_{2}\) is the proportion of sample 2 with sample size \(n_{2}\) and \(x_{2}\) number of trials.

How to Calculate Z Test Statistic?

The most important step in calculating the z test statistic is to interpret the problem correctly. It is necessary to determine which tailed test needs to be conducted and what type of test does the z statistic belong to. Suppose a teacher claims that his section's students will score higher than his colleague's section. The mean score is 22.1 for 60 students belonging to his section with a standard deviation of 4.8. For his colleague's section, the mean score is 18.8 for 40 students and the standard deviation is 8.1. Test his claim at \(\alpha\) = 0.05. The steps to calculate the z test statistic are as follows:

• Identify the type of test. In this example, the means of two populations have to be compared in one direction thus, the test is a right-tailed two-sample z test.
• Set up the hypotheses. \(H_{0}\): \(\mu_{1} = \mu_{2}\), \(H_{1}\): \(\mu_{1} > \mu_{2}\).
• Find the critical value at the given alpha level using the z table. The critical value is 1.645.
• Determine the z test statistic using the appropriate formula. This is given by z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\). Substitute values in this equation. \(\overline{x_{1}}\) = 22.1, \(\sigma_{1}\) = 4.8, \(n_{1}\) = 60, \(\overline{x_{2}}\) = 18.8, \(\sigma_{2}\) = 8.1, \(n_{2}\) = 40 and \(\mu_{1} - \mu_{2} = 0\). Thus, z = 2.32
• Compare the critical value and test statistic to arrive at a conclusion. As 2.32 > 1.645 thus, the null hypothesis can be rejected. It can be concluded that there is enough evidence to support the teacher's claim that the scores of students are better in his class.

Z Test vs T-Test

Both z test and t-test are univariate tests used on the means of two datasets. The differences between both tests are outlined in the table given below:

Related Articles:

• Probability and Statistics
• Data Handling
• Summary Statistics

Important Notes on Z Test

• Z test is a statistical test that is conducted on normally distributed data to check if there is a difference in means of two data sets.
• The sample size should be greater than 30 and the population variance must be known to perform a z test.
• The one-sample z test checks if there is a difference in the sample and population mean,
• The two sample z test checks if the means of two different groups are equal.

Examples on Z Test

Example 1: A teacher claims that the mean score of students in his class is greater than 82 with a standard deviation of 20. If a sample of 81 students was selected with a mean score of 90 then check if there is enough evidence to support this claim at a 0.05 significance level.

Solution: As the sample size is 81 and population standard deviation is known, this is an example of a right-tailed one-sample z test.

\(H_{0}\) : \(\mu = 82\)

\(H_{1}\) : \(\mu > 82\)

From the z table the critical value at \(\alpha\) = 1.645

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) = 90, \(\mu\) = 82, n = 81, \(\sigma\) = 20

As 3.6 > 1.645 thus, the null hypothesis is rejected and it is concluded that there is enough evidence to support the teacher's claim.

Answer: Reject the null hypothesis

Example 2: An online medicine shop claims that the mean delivery time for medicines is less than 120 minutes with a standard deviation of 30 minutes. Is there enough evidence to support this claim at a 0.05 significance level if 49 orders were examined with a mean of 100 minutes?

Solution: As the sample size is 49 and population standard deviation is known, this is an example of a left-tailed one-sample z test.

\(H_{0}\) : \(\mu = 120\)

\(H_{1}\) : \(\mu < 120\)

From the z table the critical value at \(\alpha\) = -1.645. A negative sign is used as this is a left tailed test.

\(\overline{x}\) = 100, \(\mu\) = 120, n = 49, \(\sigma\) = 30

As -4.66 < -1.645 thus, the null hypothesis is rejected and it is concluded that there is enough evidence to support the medicine shop's claim.

Example 3: A company wants to improve the quality of products by reducing defects and monitoring the efficiency of assembly lines. In assembly line A, there were 18 defects reported out of 200 samples while in line B, 25 defects out of 600 samples were noted. Is there a difference in the procedures at a 0.05 alpha level?

Solution: This is an example of a two-tailed two proportion z test.

\(H_{0}\): The two proportions are the same.

\(H_{1}\): The two proportions are not the same.

As this is a two-tailed test the alpha level needs to be divided by 2 to get 0.025.

Using this, the critical value from the z table is 1.96.

\(n_{1}\) = 200, \(n_{2}\) = 600

\(p_{1}\) = 18 / 200 = 0.09

\(p_{2}\) = 25 / 600 = 0.0416

p = (18 + 25) / (200 + 600) = 0.0537

z =\(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\) = 2.62

As 2.62 > 1.96 thus, the null hypothesis is rejected and it is concluded that there is a significant difference between the two lines.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Z Test

What is a z test in statistics.

A z test in statistics is conducted on data that is normally distributed to test if the means of two datasets are equal. It can be performed when the sample size is greater than 30 and the population variance is known.

What is a One-Sample Z Test?

A one-sample z test is used when the population standard deviation is known, to compare the sample mean and the population mean. The z test statistic is given by the formula \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

What is the Two-Sample Z Test Formula?

The two sample z test is used when the means of two populations have to be compared. The z test formula is given as \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is a One Proportion Z test?

A one proportion z test is used to check if the value of the observed proportion is different from the value of the theoretical proportion. The z statistic is given by \(\frac{p-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\).

What is a Two Proportion Z Test?

When the proportions of two samples have to be compared then the two proportion z test is used. The formula is given by \(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\).

How Do You Find the Z Test?

The steps to perform the z test are as follows:

• Set up the null and alternative hypotheses.
• Find the critical value using the alpha level and z table.
• Calculate the z statistic.
• Compare the critical value and the test statistic to decide whether to reject or not to reject the null hypothesis.

What is the Difference Between the Z Test and the T-Test?

A z test is used on large samples n ≥ 30 and normally distributed data while a t-test is used on small samples (n < 30) following a student t distribution . Both tests are used to check if the means of two datasets are the same.

Introduction to Statistics and Data Analysis

Chapter 6 hypothesis testing: the z-test.

We’ve all had the experience of standing at a crosswalk waiting staring at a pedestrian traffic light showing the little red man. You’re waiting for the little green man so you can cross. After a little while you’re still waiting and there aren’t any cars around. You might think ‘this light is really taking a long time’, but you continue waiting. Minutes pass and there’s still no little green man. At some point you come to the conclusion that the light is broken and you’ll never see that little green man. You cross on the little red man when it’s clear.

You may not have known this but you just conducted a hypothesis test. When you arrived at the crosswalk, you assumed that the light was functioning properly, although you will always entertain the possibility that it’s broken. In terms of hypothesis testing, your ‘null hypothesis’ is that the light is working and your ‘alternative hypothesis’ is that it’s broken. As time passes, it seems less and less likely that light is working properly. Eventually, the probability of the light working given how long you’ve been waiting becomes so low that you reject the null hypothesis in favor of the alternative hypothesis.

This sort of reasoning is the backbone of hypothesis testing and inferential statistics. It’s also the point in the course where we turn the corner from descriptive statistics to inferential statistics. Rather than describing our data in terms of means and plots, we will now start using our data to make inferences, or generalizations, about the population that our samples are drawn from. In this course we’ll focus on standard hypothesis testing where we set up a null hypothesis and determine the probability of our observed data under the assumption that the null hypothesis is true (the much maligned p-value). If this probability is small enough, then we conclude that our data suggests that the null hypothesis is false, so we reject it.

In this chapter, we’ll introduce hypothesis testing with examples from a ‘z-test’, when we’re comparing a single mean to what we’d expect from a population with known mean and standard deviation. In this case, we can convert our observed mean into a z-score for the standard normal distribution. Hence the name z-test.

It’s time to introduce the hypothesis test flow chart . It’s pretty self explanatory, even if you’re not familiar with all of these hypothesis tests. The z-test is (1) based on means, (2) with only one mean, and (3) where we know \(\sigma\) , the standard deviation of the population. Here’s how to find the z-test in the flow chart:

6.1 Women’s height example

Let’s work with the example from the end of the last chapter where we started with the fact that the heights of US women has a mean of 63 and a standard deviation of 2.5 inches. We calculated that the average height of the 122 women in Psych 315 is 64.7 inches. We then used the central limit theorem and calculated the probability of a random sample 122 heights from this population having a mean of 64.7 or greater is 2.4868996^{-14}. This is a very, very small number.

Here’s how we do it using R:

Let’s think of our sample as a random sample of UW psychology students, which is a reasonable assumption since all psychology students have to take a statistics class. What does this sample say about the psychology students that are women at UW compared to the US population? It could be that these psychology students at UW have the same mean and standard deviation as the US population, but our sample just happens to have an unusual number of tall women, but we calculated that the probability of this happening is really low. Instead, it makes more sense that the population that we’re drawing from has a mean that’s greater than the US population mean. Notice that we’re making a conclusion about the whole population of women psychology students based on our one sample.

Using the terminology of hypothesis testing, we first assumed the null hypothesis that UW women psych students have the same mean (and standard deviation) as the US population. The null hypothesis is written as:

\[ H_{0}: \mu = 63 \] In this example, our alternative hypothesis is that the mean of our population is larger than the mean of null hypothesis population. We write this as:

\[ H_{A}: \mu > 63 \]

Next, after obtaining a random sample and calculate the mean, we calculate the probability of drawing a mean this large (or larger) from the null hypothesis distribution.

If this probability is low enough, we reject the null hypothesis in favor of the alternative hypothesis. When our probability allows us to reject the null hypothesis, we say that our observed results are ‘statistically significant’.

In statistics terms, we never say we ‘accept that alternative hypothesis’ as true. All we can say is that we don’t think the null hypothesis is true. I know it’s subtle, but in science can never prove that a hypothesis is true or not. There’s always the possibility that we just happened to grab an unusual sample from the null hypothesis distribution.

6.2 The hated p<.05

The probability that we obtain our observed mean or greater given that the null hypothesis is true is called the p-value. How improbable is improbable enough to reject the null hypothesis? The p-value for our example above on women’s heights is astronomically low, so it’s clear that we should reject \(H_{0}\) .

The p-value that’s on the border of rejection is called the alpha ( \(\alpha\) ) value. We reject \(H_{0}\) when our p-value is less than \(\alpha\) .

You probably know that the most common value of alpha is \(\alpha = .05\) .

The first publication of this value dates back to Sir Ronald Fisher, in his seminal 1925 book Statistical Methods for Research Workers where he states:

“It is convenient to take this point as a limit in judging whether a deviation is considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant.” (p. 47)

If you read the chapter on the normal distribution, then you should know that 95% of the area under the normal distribution lies within \(\pm\) two standard deviations of the mean. So the probability of obtaining a sample that exceeds two standard deviations from the mean (in either direction) is .05.

6.3 IQ example

Let’s do an example using IQ scores. IQ scores are normalized to have a mean of 100 and a standard deviation of 15 points. Because they’re normalized, they are a rare example of a population which has a known mean and standard deviation. In the next chapter we’ll discuss the t-test, which is used in the more common situation when we don’t know the population standard deviation.

Suppose you have the suspicion that graduate students have higher IQ’s than the general population. You have enough time to go and measure the IQ’s of 25 randomly sampled grad students and obtain a mean of 105. Is this difference between our this observed mean and 100 statistically significant using an alpha value of \(\alpha = 0.05\) ?

Here the null hypothesis is:

\[ H_{0}: \mu = 100\]

And the alternative hypothesis is:

\[ H_{A}: \mu > 100 \]

We know that the parameters for the null hypothesis are:

\[ \mu = 100 \] and \[ \sigma = 15 \]

From this, we can calculate the probability of observing our mean of 105 or higher using the central limit theorem and what we know about the normal distribution:

\[ \sigma_{\bar{x}} = \frac{\sigma_{x}}{\sqrt{n}} = \frac{15}{\sqrt{25}} = 3 \] From this, we can calculate the probability of our observed mean using R’s ‘pnorm’ function. Here’s how to do the whole thing in R.

Since our p-value of 0.0478 is (just barely) less than our chosen value of \(\alpha = 0.05\) as our criterion, we reject \(H_{0}\) for this (contrived) example and conclude that our observed mean of 105 is significantly greater than 100, so our study suggests that the average graduate student has a higher IQ than the overall population.

You should feel uncomfortable making such a hard, binary decision for such a borderline case. After all, if we had chosen our second favorite value of alpha, \(\alpha = .01\) , we would have failed to reject \(H_{0}\) . This discomfort is a primary reason why statisticians are moving away from this discrete decision making process. Later on we’ll discuss where things are going, including reporting effect sizes, and using confidence intervals.

6.4 Alpha values vs. critical values

Using R’s qnorm function, we can find the z-score for which only 5% of the area lies above:

So the probability of a randomly sampled z-score exceeding 1.644854 is less than 5%. It follows that if we convert our observed mean into z-score values, we will reject \(H_{0}\) if and only if our z-score is greater than 1.644854. This value is called the ‘critical value’ because it lies on the boundary between rejecting and failing to reject \(H_{0}\) .

In our last example, the z-score for our observed mean is:

\[ z = \frac{X-\mu}{\frac{\sigma}{\sqrt{n}}} = \frac{105 - 100}{3} = 1.67 \] Our z-score is just barely greater than the critical value of 1.644854, which makes sense because our p-value is just barely less than 0.05.

Sometimes you’ll see textbooks will compare critical values to observed scores for the decision making process in hypothesis testing. This dates back to days were computers were less available and we had to rely on tables instead. There wasn’t enough space in a book to hold complete tables which prohibited the ability to look up a p-value for any observed value. Instead only critical values for specific values of alpha were included. If you look at really old papers, you’ll see statistics reported as \(p<.05\) or \(p<.01\) instead of actual p-values for this reason.

It may help to visualize the relationship between p-values, alpha values and critical values like this:

The red shaded region is the upper 5% of the standard normal distribution which starts at the critical value of z=1.644854. This is sometimes called the ‘rejection region’. The blue vertical line is drawn at our observed value of z=1.67. You can see that the red line falls just inside the rejection region, so we Reject \(H_{0}\) !

6.5 One vs. two-tailed tests

Recall that our alternative hypothesis was to reject if our mean IQ was significantly greater than the null hypothesis mean: \(H_{A}: \mu > 100\) . This implies that the situation where \(\mu < 100\) is never even in consideration, which is weird. In science, we’re trying to understand the true state of the world. Although we have a hunch that grad student IQ’s are higher than average, there is always the possibility that they are lower than average. If our sample came up with an IQ well below 100, we’d simply fail to reject \(H_{0}\) and move on. This feels like throwing out important information.

The test we just ran is called a ‘one-tailed’ test because we only reject \(H_{0}\) if our results fall in one of the two tails of the population distribution.

Instead, it might make more sense to reject \(H_{0}\) if we get either an unusually large or small score. This means we need two critical values - one above and one below zero. At first thought you might think we just duplicate our critical value from a one-tailed test to the other side. But will double the area of the rejection region. That’s not a good thing because if \(H_{0}\) is true, there’s actually a \(2\alpha\) probability that we’ll draw a score in the rejection region.

Instead, we divide the area into two tails, each containing an area of \(\frac{\alpha}{2}\) . For \(\alpha\) = 0.05, we can find the critical value of z with qnorm:

So with a two-tailed test at \(\alpha = 0.05\) we reject \(H_{0}\) if our observed z-score is either above z = 1.96 or less than -1.96. This is that value around 2 that Sir Ronald Fischer was talking about!

Here’s what the critical regions and observed value of z looks like for our example with a two-tailed test:

You can see that splitting the area of \(\alpha = 0.05\) into two halves increased the critical value in the positive direction from 1.64 to 1.96, making it harder to reject \(H_{0}\) . For our example, this changes our decision: our observed value of z = 1.67 no longer falls into the rejection region, so now we fail to reject \(H_{0}\) .

If we now fail to reject \(H_{0}\) , what about the p-value? Remember, for a one-tailed test, p = \(\alpha\) if our observed z-score lands right on the critical value of z. The same is true for a two-tailed test. But the z-score moved so that the area above that score is \(\frac{\alpha}{2}\) . So for a two-tailed test, in order to have a p-value of \(\alpha\) when our z-score lands right on the critical value, we need to double p-value hat we’d get for a one-tailed test.

For our example, the p-value for the one tailed test was \(p=0.0478\) . So if we use a two-tailed test, our p-value is \((2)(0.0478) = 0.0956\) . This value is greater than \(\alpha\) = 0.05, which makes sense because we just showed above that we fail to reject \(H_{0}\) with a two tailed test.

Which is the right test, one-tailed or two-tailed? Ideally, as scientists, we should be agnostic about the results of our experiment. But in reality, we all know that the results are more interesting if they are statistically significant. So you can imagine that for this example, given a choice between one and two-tailed, we’d choose a one-tailed test so that we can reject \(H_{0}\) .

There are two problems with this. First, we should never adjust our choice of hypothesis test after we observe the data. That would be an example of ‘p-hacking’, a topic we’ll discuss later. Second, most statisticians these days strongly recommend against one-tailed tests. The only reason for a one-tailed test is if there is no logical or physical possibility for a population mean to fall below the null hypothesis mean.

10 Chapter 10: Hypothesis Testing with Z

Setting up the hypotheses.

When setting up the hypotheses with z, the parameter is associated with a sample mean (in the previous chapter examples the parameters for the null used 0). Using z is an occasion in which the null hypothesis is a value other than 0. For example, if we are working with mothers in the U.S. whose children are at risk of low birth weight, we can use 7.47 pounds, the average birth weight in the US, as our null value and test for differences against that. For now, we will focus on testing a value of a single mean against what we expect from the population.

Using birthweight as an example, our null hypothesis takes the form: H 0 : μ = 7.47 Notice that we are testing the value for μ, the population parameter, NOT the sample statistic ̅X (or M). We are referring to the data right now in raw form (we have not standardized it using z yet). Again, using inferential statistics, we are interested in understanding the population, drawing from our sample observations. For the research question, we have a mean value from the sample to use, we have specific data is – it is observed and used as a comparison for a set point.

As mentioned earlier, the alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. We will set the criteria for rejecting the null hypothesis based on the directionality (greater than, less than, or not equal to) of the alternative.

If we expect our obtained sample mean to be above or below the null hypothesis value (knowing which direction), we set a directional hypothesis. O ur alternative hypothesis takes the form based on the research question itself. In our example with birthweight, this could be presented as H A : μ > 7.47 or H A : μ < 7.47. 

Note that we should only use a directional hypothesis if we have a good reason, based on prior observations or research, to suspect a particular direction. When we do not know the direction, such as when we are entering a new area of research, we use a non-directional alternative hypothesis. In our birthweight example, this could be set as H A : μ ≠ 7.47

In working with data for this course we will need to set a critical value of the test statistic for alpha (α) for use of test statistic tables in the back of the book. This is determining the critical rejection region that has a set critical value based on α.

Determining Critical Value from α

We set alpha (α) before collecting data in order to determine whether or not we should reject the null hypothesis. We set this value beforehand to avoid biasing ourselves by viewing our results and then determining what criteria we should use.

When a research hypothesis predicts an effect but does not predict a direction for the effect, it is called a non-directional hypothesis . To test the significance of a non-directional hypothesis, we have to consider the possibility that the sample could be extreme at either tail of the comparison distribution. We call this a two-tailed test .

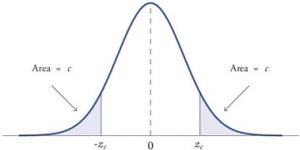
Figure 1. showing a 2-tail test for non-directional hypothesis for z for area C is the critical rejection region.

When a research hypothesis predicts a direction for the effect, it is called a directional hypothesis . To test the significance of a directional hypothesis, we have to consider the possibility that the sample could be extreme at one-tail of the comparison distribution. We call this a one-tailed test .

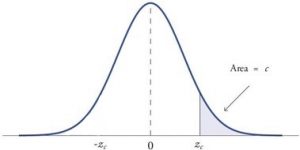
Figure 2. showing a 1-tail test for a directional hypothesis (predicting an increase) for z for area C is the critical rejection region.

Determining Cutoff Scores with Two-Tailed Tests

Typically we specify an α level before analyzing the data. If the data analysis results in a probability value below the α level, then the null hypothesis is rejected; if it is not, then the null hypothesis is not rejected. In other words, if our data produce values that meet or exceed this threshold, then we have sufficient evidence to reject the null hypothesis ; if not, we fail to reject the null (we never “accept” the null). According to this perspective, if a result is significant, then it does not matter how significant it is. Moreover, if it is not significant, then it does not matter how close to being significant it is. Therefore, if the 0.05 level is being used, then probability values of 0.049 and 0.001 are treated identically. Similarly, probability values of 0.06 and 0.34 are treated identically. Note we will discuss ways to address effect size (which is related to this challenge of NHST).

When setting the probability value, there is a special complication in a two-tailed test. We have to divide the significance percentage between the two tails. For example, with a 5% significance level, we reject the null hypothesis only if the sample is so extreme that it is in either the top 2.5% or the bottom 2.5% of the comparison distribution. This keeps the overall level of significance at a total of 5%. A one-tailed test does have such an extreme value but with a one-tailed test only one side of the distribution is considered.

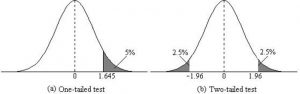
Figure 3. Critical value differences in one and two-tail tests. Photo Credit

Let’s re view th e set critical values for Z.

We discussed z-scores and probability in chapter 8.  If we revisit the z-score for 5% and 1%, we can identify the critical regions for the critical rejection areas from the unit standard normal table.

• A two-tailed test at the 5% level has a critical boundary Z score of +1.96 and -1.96
• A one-tailed test at the 5% level has a critical boundary Z score of +1.64 or -1.64
• A two-tailed test at the 1% level has a critical boundary Z score of +2.58 and -2.58
• A one-tailed test at the 1% level has a critical boundary Z score of +2.33 or -2.33.

Review: Critical values, p-values, and significance level

There are two criteria we use to assess whether our data meet the thresholds established by our chosen significance level, and they both have to do with our discussions of probability and distributions. Recall that probability refers to the likelihood of an event, given some situation or set of conditions. In hypothesis testing, that situation is the assumption that the null hypothesis value is the correct value, or that there is no effec t. The value laid out in H 0 is our condition under which we interpret our results. To reject this assumption, and thereby reject the null hypothesis, we need results that would be very unlikely if the null was true.

Now recall that values of z which fall in the tails of the standard normal distribution represent unlikely values. That is, the proportion of the area under the curve as or more extreme than z is very small as we get into the tails of the distribution. Our significance level corresponds to the area under the tail that is exactly equal to α: if we use our normal criterion of α = .05, then 5% of the area under the curve becomes what we call the rejection region (also called the critical region) of the distribution. This is illustrated in Figure 4.

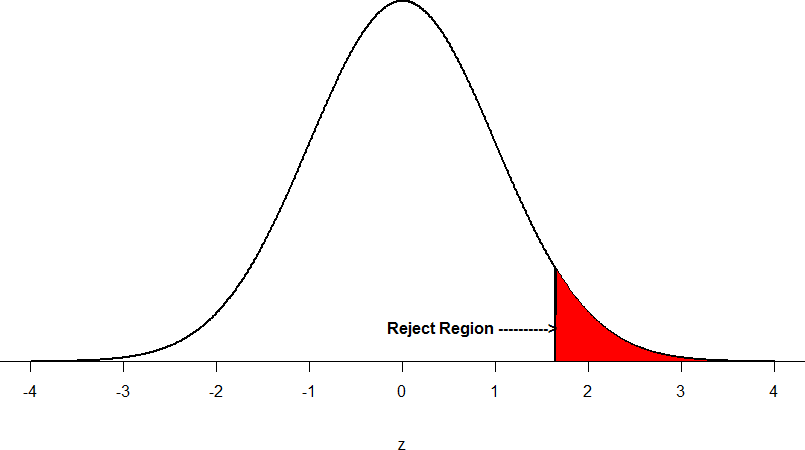
Figure 4: The rejection region for a one-tailed test

The shaded rejection region takes us 5% of the area under the curve. Any result which falls in that region is sufficient evidence to reject the null hypothesis.

The rejection region is bounded by a specific z-value, as is any area under the curve. In hypothesis testing, the value corresponding to a specific rejection region is called the critical value, z crit (“z-crit”) or z* (hence the other name “critical region”). Finding the critical value works exactly the same as finding the z-score corresponding to any area under the curve like we did in Unit 1. If we go to the normal table, we will find that the z-score corresponding to 5% of the area under the curve is equal to 1.645 (z = 1.64 corresponds to 0.0405 and z = 1.65 corresponds to 0.0495, so .05 is exactly in between them) if we go to the right and -1.645 if we go to the left. The direction must be determined by your alternative hypothesis, and drawing then shading the distribution is helpful for keeping directionality straight.

Suppose, however, that we want to do a non-directional test. We need to put the critical region in both tails, but we don’t want to increase the overall size of the rejection region (for reasons we will see later). To do this, we simply split it in half so that an equal proportion of the area under the curve falls in each tail’s rejection region. For α = .05, this means 2.5% of the area is in each tail, which, based on the z-table, corresponds to critical values of z* = ±1.96. This is shown in Figure 5.

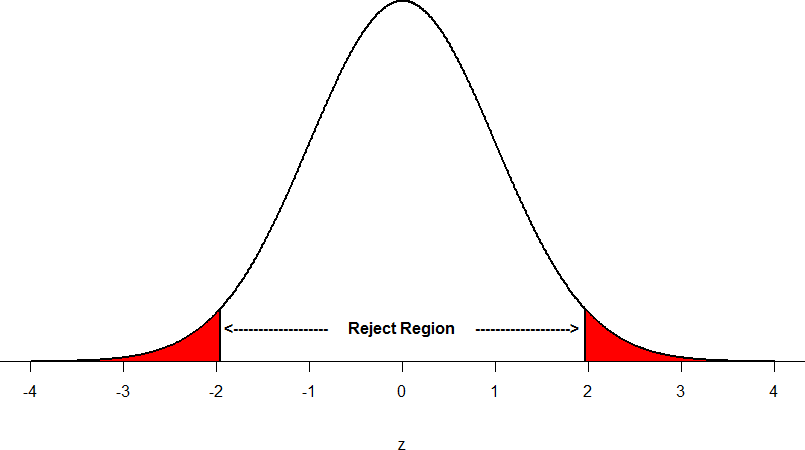
Figure 5: Two-tailed rejection region

Thus, any z-score falling outside ±1.96 (greater than 1.96 in absolute value) falls in the rejection region. When we use z-scores in this way, the obtained value of z (sometimes called z-obtained) is something known as a test statistic, which is simply an inferential statistic used to test a null hypothesis.

Calculate the test statistic: Z

Now that we understand setting up the hypothesis and determining the outcome, let’s examine hypothesis testing with z!  The next step is to carry out the study and get the actual results for our sample. Central to hypothesis test is comparison of the population and sample means. To make our calculation and determine where the sample is in the hypothesized distribution we calculate the Z for the sample data.

Make a decision

To decide whether to reject the null hypothesis, we compare our sample’s Z score to the Z score that marks our critical boundary. If our sample Z score falls inside the rejection region of the comparison distribution (is greater than the z-score critical boundary) we reject the null hypothesis.

The formula for our z- statistic has not changed:

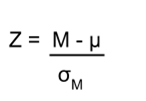
To formally test our hypothesis, we compare our obtained z-statistic to our critical z-value. If z obt > z crit , that means it falls in the rejection region (to see why, draw a line for z = 2.5 on Figure 1 or Figure 2) and so we reject H 0 . If z obt < z crit , we fail to reject. Remember that as z gets larger, the corresponding area under the curve beyond z gets smaller. Thus, the proportion, or p-value, will be smaller than the area for α, and if the area is smaller, the probability gets smaller. Specifically, the probability of obtaining that result, or a more extreme result, under the condition that the null hypothesis is true gets smaller.

Conversely, if we fail to reject, we know that the proportion will be larger than α because the z-statistic will not be as far into the tail. This is illustrated for a one- tailed test in Figure 6.

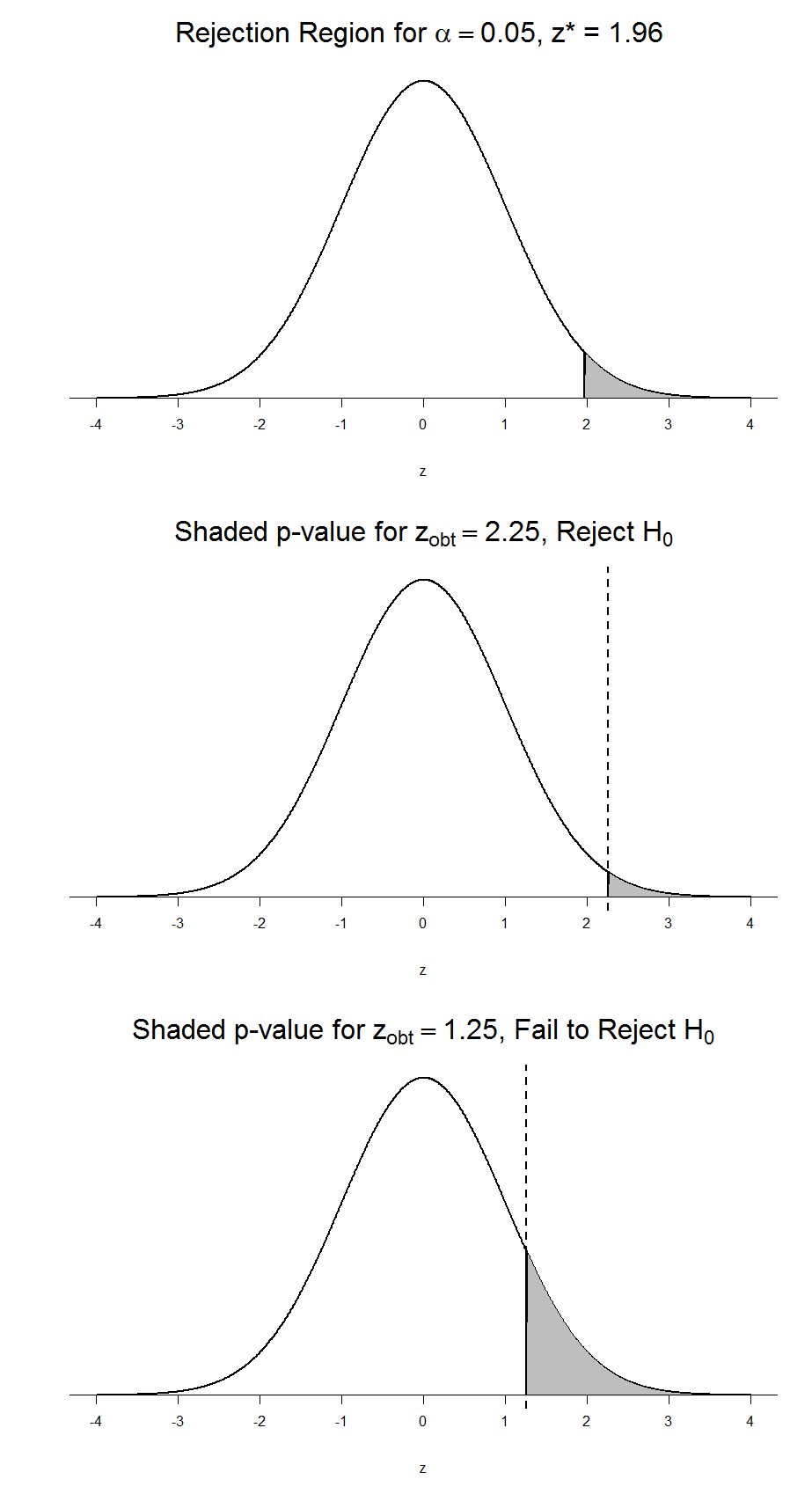
Figure 6. Relation between α, z obt , and p

When the null hypothesis is rejected, the effect is said to be statistically significant . Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough.

Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.

Review: Steps of the Hypothesis Testing Process

The process of testing hypotheses follows a simple four-step procedure. This process will be what we use for the remained of the textbook and course, and though the hypothesis and statistics we use will change, this process will not.

Step 1: State the Hypotheses

Your hypotheses are the first thing you need to lay out. Otherwise, there is nothing to test! You have to state the null hypothesis (which is what we test) and the alternative hypothesis (which is what we expect). These should be stated mathematically as they were presented above AND in words, explaining in normal English what each one means in terms of the research question.

Step 2: Find the Critical Values

Next, we formally lay out the criteria we will use to test our hypotheses. There are two pieces of information that inform our critical values: α, which determines how much of the area under the curve composes our rejection region, and the directionality of the test, which determines where the region will be.

Step 3: Compute the Test Statistic

Once we have our hypotheses and the standards we use to test them, we can collect data and calculate our test statistic, in this case z . This step is where the vast majority of differences in future chapters will arise: different tests used for different data are calculated in different ways, but the way we use and interpret them remains the same.

Step 4: Make the Decision

Finally, once we have our obtained test statistic, we can compare it to our critical value and decide whether we should reject or fail to reject the null hypothesis. When we do this, we must interpret the decision in relation to our research question, stating what we concluded, what we based our conclusion on, and the specific statistics we obtained.

Example: Movie Popcorn

Let’s see how hypothesis testing works in action by working through an example. Say that a movie theater owner likes to keep a very close eye on how much popcorn goes into each bag sold, so he knows that the average bag has 8 cups of popcorn and that this varies a little bit, about half a cup. That is, the known population mean is μ = 8.00 and the known population standard deviation is σ =0.50. The owner wants to make sure that the newest employee is filling bags correctly, so over the course of a week he randomly assesses 25 bags filled by the employee to test for a difference (n = 25). He doesn’t want bags overfilled or under filled, so he looks for differences in both directions. This scenario has all of the information we need to begin our hypothesis testing procedure.

Our manager is looking for a difference in the mean cups of popcorn bags compared to the population mean of 8. We will need both a null and an alternative hypothesis written both mathematically and in words. We’ll always start with the null hypothesis:

H 0 : There is no difference in the cups of popcorn bags from this employee H 0 : μ = 8.00

Notice that we phrase the hypothesis in terms of the population parameter μ, which in this case would be the true average cups of bags filled by the new employee.

Our assumption of no difference, the null hypothesis, is that this mean is exactly

the same as the known population mean value we want it to match, 8.00. Now let’s do the alternative:

H A : There is a difference in the cups of popcorn bags from this employee H A : μ ≠ 8.00

In this case, we don’t know if the bags will be too full or not full enough, so we do a two-tailed alternative hypothesis that there is a difference.

Our critical values are based on two things: the directionality of the test and the level of significance. We decided in step 1 that a two-tailed test is the appropriate directionality. We were given no information about the level of significance, so we assume that α = 0.05 is what we will use. As stated earlier in the chapter, the critical values for a two-tailed z-test at α = 0.05 are z* = ±1.96. This will be the criteria we use to test our hypothesis. We can now draw out our distribution so we can visualize the rejection region and make sure it makes sense

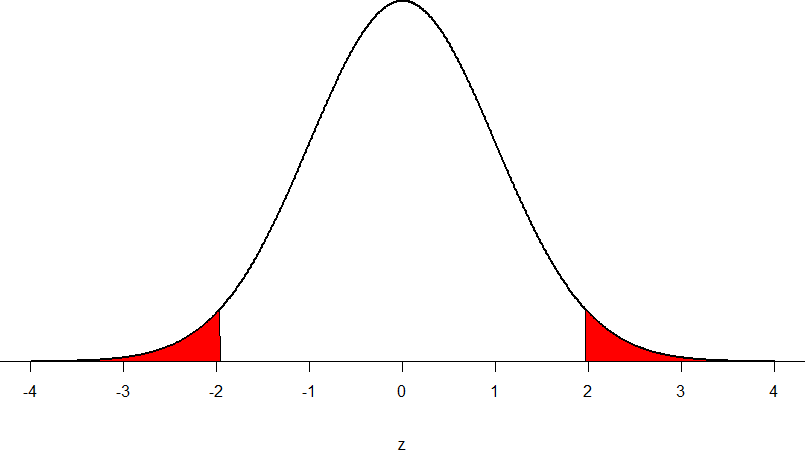
Figure 7: Rejection region for z* = ±1.96

Step 3: Calculate the Test Statistic

Now we come to our formal calculations. Let’s say that the manager collects data and finds that the average cups of this employee’s popcorn bags is ̅X = 7.75 cups. We can now plug this value, along with the values presented in the original problem, into our equation for z:

So our test statistic is z = -2.50, which we can draw onto our rejection region distribution:

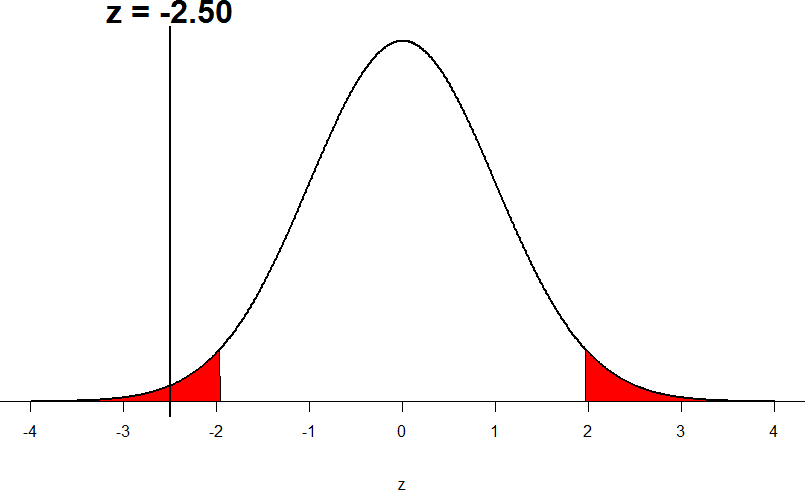
Figure 8: Test statistic location

Looking at Figure 5, we can see that our obtained z-statistic falls in the rejection region. We can also directly compare it to our critical value: in terms of absolute value, -2.50 > -1.96, so we reject the null hypothesis. We can now write our conclusion:

When we write our conclusion, we write out the words to communicate what it actually means, but we also include the average sample size we calculated (the exact location doesn’t matter, just somewhere that flows naturally and makes sense) and the z-statistic and p-value. We don’t know the exact p-value, but we do know that because we rejected the null, it must be less than α.

Effect Size

When we reject the null hypothesis, we are stating that the difference we found was statistically significant, but we have mentioned several times that this tells us nothing about practical significance. To get an idea of the actual size of what we found, we can compute a new statistic called an effect size. Effect sizes give us an idea of how large, important, or meaningful a statistically significant effect is.

For mean differences like we calculated here, our effect size is Cohen’s d :

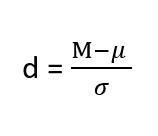
Effect sizes are incredibly useful and provide important information and clarification that overcomes some of the weakness of hypothesis testing. Whenever you find a significant result, you should always calculate an effect size

Table 1. Interpretation of Cohen’s d

Example: Office Temperature

Let’s do another example to solidify our understanding. Let’s say that the office building you work in is supposed to be kept at 74 degree Fahrenheit but is allowed

to vary by 1 degree in either direction. You suspect that, as a cost saving measure, the temperature was secretly set higher. You set up a formal way to test your hypothesis.

You start by laying out the null hypothesis:

H 0 : There is no difference in the average building temperature H 0 : μ = 74

Next you state the alternative hypothesis. You have reason to suspect a specific direction of change, so you make a one-tailed test:

H A : The average building temperature is higher than claimed H A : μ > 74

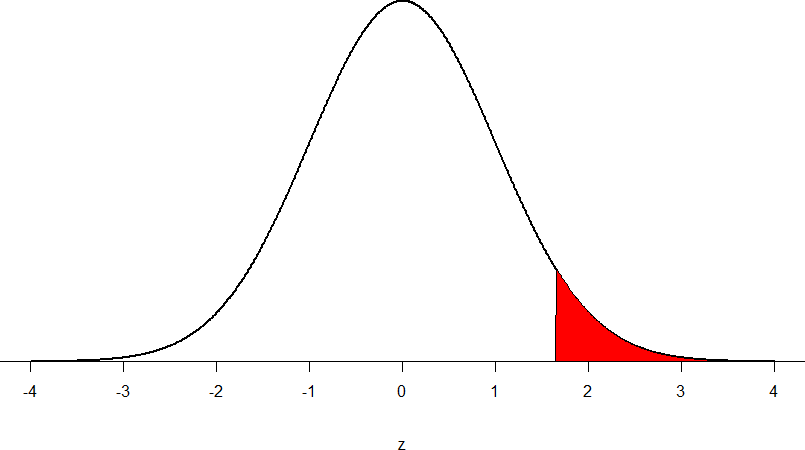
Now that you have everything set up, you spend one week collecting temperature data:

You calculate the average of these scores to be 𝑋̅ = 76.6 degrees. You use this to calculate the test statistic, using μ = 74 (the supposed average temperature), σ = 1.00 (how much the temperature should vary), and n = 5 (how many data points you collected):

z = 76.60 − 74.00 = 2.60    = 5.78

          1.00/√5            0.45

This value falls so far into the tail that it cannot even be plotted on the distribution!

Figure 7: Obtained z-statistic

You compare your obtained z-statistic, z = 5.77, to the critical value, z* = 1.645, and find that z > z*. Therefore you reject the null hypothesis, concluding: Based on 5 observations, the average temperature (𝑋̅ = 76.6 degrees) is statistically significantly higher than it is supposed to be, z = 5.77, p < .05.

d = (76.60-74.00)/ 1= 2.60

The effect size you calculate is definitely large, meaning someone has some explaining to do!

Example: Different Significance Level

First, let’s take a look at an example phrased in generic terms, rather than in the context of a specific research question, to see the individual pieces one more time. This time, however, we will use a stricter significance level, α = 0.01, to test the hypothesis.

We will use 60 as an arbitrary null hypothesis value: H 0 : The average score does not differ from the population H 0 : μ = 50

We will assume a two-tailed test: H A : The average score does differ H A : μ ≠ 50

We have seen the critical values for z-tests at α = 0.05 levels of significance several times. To find the values for α = 0.01, we will go to the standard normal table and find the z-score cutting of 0.005 (0.01 divided by 2 for a two-tailed test) of the area in the tail, which is z crit * = ±2.575. Notice that this cutoff is much higher than it was for α = 0.05. This is because we need much less of the area in the tail, so we need to go very far out to find the cutoff. As a result, this will require a much larger effect or much larger sample size in order to reject the null hypothesis.

We can now calculate our test statistic.  The average of 10 scores is M = 60.40 with a µ = 60. We will use σ = 10 as our known population standard deviation. From this information, we calculate our z-statistic as:

Our obtained z-statistic, z = 0.13, is very small. It is much less than our critical value of 2.575. Thus, this time, we fail to reject the null hypothesis. Our conclusion would look something like:

Notice two things about the end of the conclusion. First, we wrote that p is greater than instead of p is less than, like we did in the previous two examples. This is because we failed to reject the null hypothesis. We don’t know exactly what the p- value is, but we know it must be larger than the α level we used to test our hypothesis. Second, we used 0.01 instead of the usual 0.05, because this time we tested at a different level. The number you compare to the p-value should always be the significance level you test at. Because we did not detect a statistically significant effect, we do not need to calculate an effect size. Note: some statisticians will suggest to always calculate effects size as a possibility of Type II error. Although insignificant, calculating d = (60.4-60)/10 = .04 which suggests no effect (and not a possibility of Type II error).

Review Considerations in Hypothesis Testing

Errors in hypothesis testing.

Keep in mind that rejecting the null hypothesis is not an all-or-nothing decision. The Type I error rate is affected by the α level: the lower the α level the lower the Type I error rate. It might seem that α is the probability of a Type I error. However, this is not correct. Instead, α is the probability of a Type I error given that the null hypothesis is true. If the null hypothesis is false, then it is impossible to make a Type I error. The second type of error that can be made in significance testing is failing to reject a false null hypothesis. This kind of error is called a Type II error.

Statistical Power

The statistical power of a research design is the probability of rejecting the null hypothesis given the sample size and expected relationship strength. Statistical power is the complement of the probability of committing a Type II error. Clearly, researchers should be interested in the power of their research designs if they want to avoid making Type II errors. In particular, they should make sure their research design has adequate power before collecting data. A common guideline is that a power of .80 is adequate. This means that there is an 80% chance of rejecting the null hypothesis for the expected relationship strength.

Given that statistical power depends primarily on relationship strength and sample size, there are essentially two steps you can take to increase statistical power: increase the strength of the relationship or increase the sample size. Increasing the strength of the relationship can sometimes be accomplished by using a stronger manipulation or by more carefully controlling extraneous variables to reduce the amount of noise in the data (e.g., by using a within-subjects design rather than a between-subjects design). The usual strategy, however, is to increase the sample size. For any expected relationship strength, there will always be some sample large enough to achieve adequate power.

Inferential statistics uses data from a sample of individuals to reach conclusions about the whole population. The degree to which our inferences are valid depends upon how we selected the sample (sampling technique) and the characteristics (parameters) of population data. Statistical analyses assume that sample(s) and population(s) meet certain conditions called statistical assumptions.

It is easy to check assumptions when using statistical software and it is important as a researcher to check for violations; if violations of statistical assumptions are not appropriately addressed then results may be interpreted incorrectly.

Learning Objectives

Having read the chapter, students should be able to:

• Conduct a hypothesis test using a z-score statistics, locating critical region, and make a statistical decision including.
• Explain the purpose of measuring effect size and power, and be able to compute Cohen’s d.

Exercises – Ch. 10

• List the main steps for hypothesis testing with the z-statistic. When and why do you calculate an effect size?
• z = 1.99, two-tailed test at α = 0.05
• z = 1.99, two-tailed test at α = 0.01
• z = 1.99, one-tailed test at α = 0.05
• You are part of a trivia team and have tracked your team’s performance since you started playing, so you know that your scores are normally distributed with μ = 78 and σ = 12. Recently, a new person joined the team, and you think the scores have gotten better. Use hypothesis testing to see if the average score has improved based on the following 8 weeks’ worth of score data: 82, 74, 62, 68, 79, 94, 90, 81, 80.
• A study examines self-esteem and depression in teenagers.  A sample of 25 teens with a low self-esteem are given the Beck Depression Inventory.  The average score for the group is 20.9.  For the general population, the average score is 18.3 with σ = 12.  Use a two-tail test with α = 0.05 to examine whether teenagers with low self-esteem show significant differences in depression.
• You get hired as a server at a local restaurant, and the manager tells you that servers’ tips are $42 on average but vary about $12 (μ = 42, σ = 12). You decide to track your tips to see if you make a different amount, but because this is your first job as a server, you don’t know if you will make more or less in tips. After working 16 shifts, you find that your average nightly amount is $44.50 from tips. Test for a difference between this value and the population mean at the α = 0.05 level of significance.

Answers to Odd- Numbered Exercises – Ch. 10

1. List hypotheses. Determine critical region. Calculate z.  Compare z to critical region. Draw Conclusion.  We calculate an effect size when we find a statistically significant result to see if our result is practically meaningful or important

5. Step 1: H 0 : μ = 42 “My average tips does not differ from other servers”, H A : μ ≠ 42 “My average tips do differ from others”

Introduction to Statistics for Psychology Copyright © 2021 by Alisa Beyer is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book