prime factor problem solving

Prime Factorization

Prime numbers.

A Prime Number is:

a whole number above 1 that cannot be made by multiplying other whole numbers

When it can  be made by multiplying other whole numbers it is a Composite Number , like this:

(The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19 and 23, and we have a prime number chart if you need more.)

"Factors" are the numbers you multiply together to get another number:

"Prime Factorization" is finding which prime numbers multiply together to make the original number.

Here are some examples:

Example: What are the prime factors of 12 ?

It is best to start working from the smallest prime number, which is 2, so let's check:

Yes, it divided exactly by 2. We have taken the first step!

But 6 is not a prime number, so we need to go further. Let's try 2 again:

Yes, that worked also. And 3 is a prime number, so we have the answer:

12 = 2 × 2 × 3

As you can see, every factor is a prime number , so the answer is right.

It is neater to show repeated numbers using  exponents :

• Without exponents:  2 × 2 × 3
• With exponents:  2 2 × 3

Example: What is the prime factorization of 147 ?

Can we divide 147 exactly by 2?

147 ÷ 2 = 73½

No we can't. The answer should be a whole number, and 73½ is not.

Let's try the next prime number, 3:

147 ÷ 3 = 49

That worked, now try factoring 49.

The next prime, 5, does not work. But 7 does, so we get:

And that is as far as we need to go, because all the factors are prime numbers.

147 = 3 × 7 × 7 = 3 × 7 2

Example: What is the prime factorization of 17 ?

Hang on ... 17 is a Prime Number .

So that is as far as we can go.

Another Method

We just did factorization by starting at the smallest prime and working upwards.

But sometimes it is easier to break a number down into any factors we can ... then work those factor down to primes.

Example: What are the prime factors of 90 ?

Break 90 into 9 × 10

• The prime factors of 9 are 3 and 3
• The prime factors of 10 are 2 and 5

So the prime factors of 90 are 3, 3, 2 and 5

90 = 2 × 3 2 × 5

Factor Tree

A "Factor Tree" can help: find any factors of the number, then the factors of those numbers, etc, until we can't factor any more.

Example: 48

48 = 8 × 6 , so we write down "8" and "6" below 48

Now we continue and factor 8 into 4 × 2

Then 4 into 2 × 2

And lastly 6 into 3 × 2

We can't factor any more, so we have found the prime factors.

Which reveals that 48 = 2 × 2 × 2 × 2 × 3

48 = 2 4 × 3

Why find Prime Factors?

A prime number can only be divided by 1 or itself, so it cannot be factored any further!

Every other whole number can be broken down into prime number factors.

This idea can be very useful when working with big numbers, such as in Cryptography.

Cryptography

Cryptography is the study of secret codes. Prime Factorization is important to people who try to make (or break) secret codes based on numbers.

That is because factoring very large numbers is very hard, and can take computers a long time to do.

And here is another thing:

There is only one (unique!) set of prime factors for any number.

Example: the prime factors of 330 are 2, 3, 5 and 11

330 = 2 × 3 × 5 × 11

There is no other possible set of prime numbers that can be multiplied to make 330.

This idea is so important it is called the Fundamental Theorem of Arithmetic .

Prime Factorization Tool

OK, we have one more method ... use our Prime Factorization Tool that can work out the prime factors for numbers up to 9007199254740991.

Prime Factorisation Questions

Prime factorisation questions given here with solutions will help students understand the concept of prime factorisation and how to use the concept to solve various types of problems. Students must practice these questions to score well in their examinations.

Also read: How to find prime factors?

Prime Factorisation Questions with Solutions

Now that we understand what is meant by prime factorisation, let us practice prime factorisation by solving the following questions.

Question 1: Find the prime factorisation of the following:

∴ Prime Factorisation of 284 = 2 × 2 × 71

∴ Prime factorisation of 7084 = 2 × 2 × 7 × 11 × 23.

∴ Prime factorisation of 5595 = 3 × 5 × 373.

Question 2: Find the prime factorisation of the following:

∴ Prime Factorisation of 23356 = 2 × 2 × 5839

∴ Prime Factorisation of 23356 = 2 × 3 × 31 × 269

∴ Prime Factorisation of 23356 = 11 × 317

∴ Prime Factorisation of 23356 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 13 = 2 5 × 3 2 × 5 × 13

Question 3: State ‘true’ or ‘false’ for the following:

(i) 177 is a prime number

(ii) 1 is a composite number

(iii) The prime factorisation of 252 is 2 2 × 3 3 × 7.

(iv) 5 × 33 is the prime factorisation of 165.

(i) 177 is a prime number. (False)

(ii) 1 is a composite number. (False)

(iii) The prime factorisation of 252 is 2 2 × 3 3 × 7. (True)

(iv) 5 × 33 is the prime factorisation of 165. (False)

Question 4: List the common prime factors of 256 and 156.

Prime factorisation of 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

Prime factorisation of 156 = 2 × 2 × 3 × 13

The common prime factor of 256 and 156 is 2.

Question 5: List the common factors of 152 and 76.

Prime factorisation of 152 = 2 × 2 × 2 × 19

Prime factorisation of 76 = 2 × 2 × 19

The common prime factors of 152 and 76 are 2 and 19.

• HCF and LCM
• Factors and Multiples
• Prime Factorisation Calculator

Question 6: Find the highest common factor of 34, 42 and 58.

Prime factorisation of 34 = 2 × 17

Prime factorisation of 42 = 2 × 3 × 7

Prime factorisation of 58 = 2 × 29

The highest common factor of 34, 42, and 58 is 2.

Question 7: Find the lowest common multiple of 45, 75, and 125.

Prime factorisation of 45 = 3 × 3 × 5

Prime factorisation of 75 = 3 × 5 × 5

Prime factorisation of 125 = 5 × 5 × 5

Lowest common multiple of 45, 65 and 125 = 3 × 3 × 5 × 5 × 5 = 1125.

Question 8: Fill in the blank:

(i) 435 = 3 × ___ × ____.

(ii) 378 = 2 × __ × 3 × ___ × ____.

(iii) 1125 = 3 __ × 5 __ .

(i) 435 = 3 × 5 × 9.

(ii) 378 = 2 × 3 × 3 × 3 × 7.

(iii) 1125 = 3 2 × 5 3 .

Question 9: Find the prime factorisation of 118724.

The prime factorisation of 118724 is 2 × 2 × 67 × 443.

Question 10: Verify:

Prime factorisation of 284 × Prime factorisation of 456 = Prime factorisation of (284 × 456)

Prime factorisation of 284 = 2 × 2 × 71

Prime factorisation of 456 = 2 × 2 × 2 × 3 × 19

Prime factorisation of (283 × 456) = prime factorisation of 129504

= 2 × 2 × 2 × 2 × 2 × 3 × 19 × 71

Prime factorisation of 284 × Prime factorisation of 456 = Prime factorisation of (284 × 456).

Related Video on Common Factors

Practice Questions on Prime Factorisation

1. Find the prime factorisation of following:

2. Find the common prime factors of the following:

(i) 25, 65, and 55

(ii) 134 and 345

(iii) 36, 48, and 58

3. Find the lowest common multiple of the following:

(i) 34 and 45

(ii) 45, 24, and 16

(iii) 32, 16, and 18.

Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Prime Factorization

• Practice Questions

Prime factorization, the process of breaking down a number into the set of prime numbers that multiply together to result in the original number, is a cornerstone of number theory. Through engaging examples and clear, concise explanations, this guide aims to demystify the process, showcasing its practicality and importance in various mathematical applications, from solving greatest common divisor (GCD) problems to simplifying fractions. Whether you’re tackling homework problems or exploring mathematical theories, mastering prime factorization is a skill that enhances both academic and real-world mathematical proficiency.

What is Prime Factorization?

Prime factorization is the method of expressing a number as the product of its prime factors. This fundamental concept in mathematics involves breaking down a composite number into a combination of prime numbers that, when multiplied together, give back the original number. For example, the prime factorization of 12 is 2 x 2 x 3, indicating that when the prime numbers 2 and 3 are multiplied together in this manner, the result is 12. Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions and finding the least common multiple (LCM) or greatest common divisor (GCD) of two numbers. It’s a key skill that enhances one’s ability to work with numbers and solve a wide range of mathematical problems.

Prime Factorization Solved Examples

Here are several examples of prime factorization, demonstrating how to break down composite numbers into their prime factors:

Example 1: Prime Factorization of 18

• Factors: 2 × 3 × 3 or 2 × 3 2
• Explanation: 18 can be divided by 2 to get 9, which can then be divided by 3 twice, resulting in the prime factors 2 and 3.

Example 2: Prime Factorization of 30

• Factors: 2 × 3 × 5
• Explanation: 30 is divisible by 2 to get 15, which can then be divided by 3 to get 5; all divisors 2, 3, and 5 are prime.

Example 3: Prime Factorization of 100

• Number: 100
• Factors: 2×2×5×5 or 2 2 ×5 5
• Explanation: 100 is divisible by 2 to get 50, which is again divisible by 2 to get 25, which can then be divided by 5 twice, yielding prime factors 2 and 5.

Example 4: Prime Factorization of 60

• Factors: 2×2×5×5 or 22×3×5
• Explanation: Starting with 60, it is divisible by 2 twice to get 15, which is then divisible by 3 and 5, revealing the prime numbers 2, 3, and 5.

Example 5: Prime Factorization of 84

• Factors: 2×2×3×7 or 2 2 ×3×7
• Explanation: 84 can be divided by 2 to get 42, which is again divisible by 2 to get 21, and then by 3 to get 7, showing that 84’s prime factors are 2, 3, and 7.

Prime Factorization of a Number

Methods of Prime Factorization

There are various methods for the prime factorization of a number. The most common methods that are used for prime factorization are given below:

• Prime factorization by factor tree method
• Prime factorization by division method

Prime Factorization by Factor Tree Method

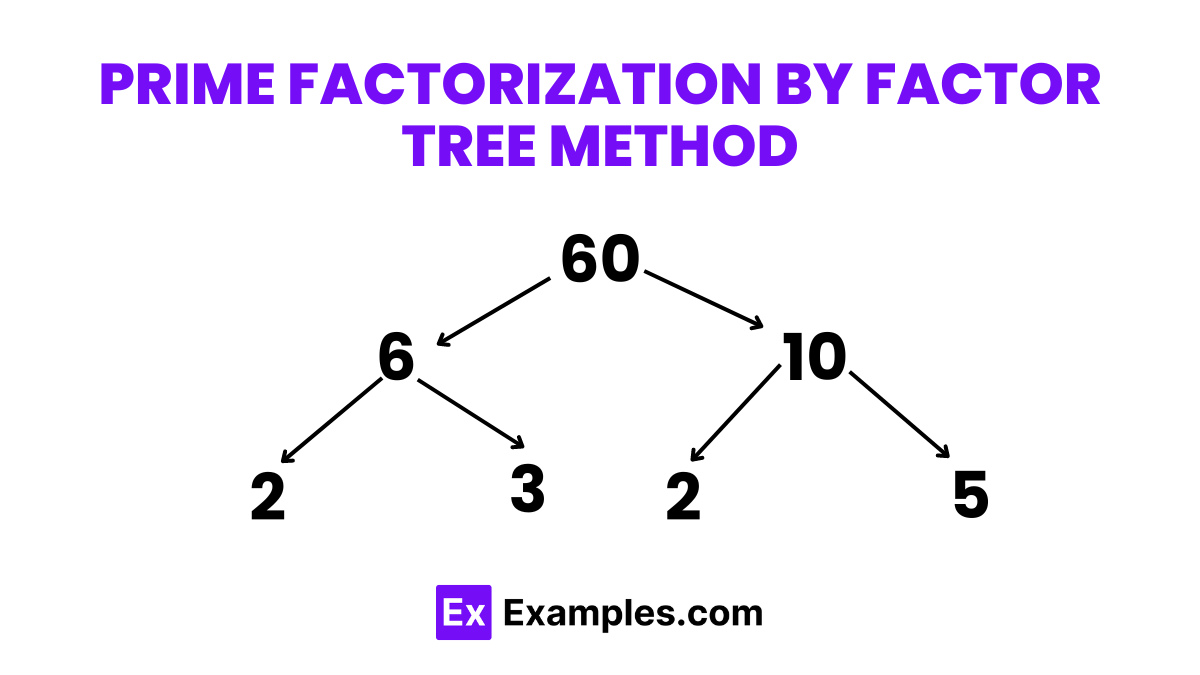
The factor tree method involves breaking down a number into its prime factors by creating a tree diagram. Each branch of the tree splits the number into factors, continuing until all branches end in prime numbers.

Example: Factorize 60 using the factor tree method.

Solution Steps:

• Start with 60. Split it into any two factors. Let’s use 6 and 10.
• Break down 6 into 2 and 3, both prime numbers, so these branches end here.
• Break down 10 into 2 and 5, also prime numbers.
• Result: The prime factorization of 60 is 2 × 2 × 3 × 5 or 2 2 × 3 × 5

Prime Factorization by Division Method

The division method for prime factorization involves dividing the number by the smallest possible prime number (2, 3, 5, etc.) until the result is 1. At each step, the divisor that results in a whole number is a prime factor.

Example: Factorize 60 using the division method.

• 60 ÷ 2 = 30 . So, 2 is a prime factor.
• 30 ÷ 2 = 15 . 2 is a prime factor again.
• 15 ÷ 3 = 5 . So, 3 is a prime factor.
• 5 ÷ 5 = 1 . 5 is the last prime factor.
• Result: The prime factorization of 60 is 2 × 2 × 3 × 5 or 2 2 × 3 × 5.

These methods offer systematic ways to break down a number into its prime components, each providing a clear pathway through either visual representation or sequential division to arrive at the prime factorization of a number.

Applications of Prime Factorization

Prime factorization, the process of breaking down a number into its prime number components, serves as a cornerstone in mathematics with broad applications. It is crucial for simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving Diophantine equations.

Example: Simplifying the fraction 8/12 ​ involves prime factorizing the numerator (8 = 2 x 2 x 2) and the denominator (12 = 2 x 2 x 3), leading to its simplest form 2/3  by canceling common factors.

HCF and LCM Using Prime Factorization

Finding the highest common factor (hcf).

The HCF or GCD of two numbers is the highest number that divides both of them without leaving a remainder.

Steps with Example:

• Choose Numbers: Consider 30 and 45.
• Prime Factorize: 30 = 2 x 3 x 5; 45 = 3 x 3 x 5.
• Identify Common Factors: Common prime factors are 3 and 5.
• Multiply Common Factors: HCF = 3 x 5 = 15.

Finding the Least Common Multiple (LCM)

The LCM of two numbers is the smallest number that is a multiple of both.

• Choose Numbers: Consider 8 and 12.
• Prime Factorize: 8 = 2 x 2 x 2; 12 = 2 x 2 x 3.
• Combine Prime Factors: Use the highest power of all prime numbers found in both factorizations (2 x 2 x 2 x 3).
• Calculate LCM: LCM = 2 x 2 x 2 x 3 = 24.

These methods of using prime factorization to find HCF and LCM showcase its practical utility in solving problems that require understanding the fundamental structure of numbers.

Frequently Asked Questions on Prime Factorization

Why is prime factorization important.

It’s crucial for various mathematical applications, including simplifying fractions, finding the greatest common divisors (GCD), least common multiples (LCM), and solving problems in number theory.

Can Every Number Be Prime Factorized?

Every composite number can be prime factorized. However, prime numbers and the number 1 are exceptions; prime numbers are their own prime factors, and 1 is not considered because it does not meet the definition of a prime number.

How Do You Find the Prime Factorization of a Number?

To find the prime factorization of a number, divide the number by the smallest prime number (2) and continue dividing by prime numbers (3, 5, 7, etc.) until the quotient is a prime number.

What Is the Difference Between Prime Numbers and Prime Factors?

Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves. Prime factors are prime numbers that multiply together to give a composite number.

Is 1 a Prime Factor?

No, 1 is not considered a prime factor because it does not meet the definition of a prime number, which must have exactly two distinct positive divisors.

Can a Number Have More Than One Set of Prime Factors?

No, the Fundamental Theorem of Arithmetic states that every integer greater than 1 either is prime itself or can be uniquely represented as a product of prime numbers, up to the order of the factors.

How Does Prime Factorization Simplify Fractions?

Prime factorization helps identify common factors in the numerator and denominator of a fraction, allowing them to be cancelled out to simplify the fraction to its lowest terms.

What Role Does Prime Factorization Play in Cryptography?

In cryptography, prime factorization is used in algorithms for public key encryption, where large prime numbers and their products are fundamental to the security of encrypted data.

Are There Efficient Algorithms for Prime Factorization?

While there are algorithms that can perform prime factorization more efficiently than trial division, such as the Sieve of Eratosthenes for finding primes or the Pollard Rho algorithm for factorization, prime factorization of very large numbers remains computationally challenging, which is a basis for the security of many encryption systems.

Prime factorization is a fundamental mathematical process that breaks down composite numbers into their prime components. It’s essential for simplifying fractions, calculating GCD and LCM, and has significant applications in number theory and cryptography. Understanding prime factorization enriches one’s mathematical skills, offering a deeper insight into the structure of numbers and their properties, and highlighting its indispensable role in both academic and practical mathematics.

AI Generator

Text prompt

• Instructive
• Professional

Prime Factorization: Definition, Methods, Examples, FAQs

What is prime factorization in math, what are factors and prime factors, how to find prime factorization of a number, solved examples on prime factorization, practice problems on prime factorization, frequently asked questions on prime factorization.

Prime factorization of a number is a way of writing a number as the product of its prime factors. Thus, the meaning of prime factorization of a number is finding prime numbers which when multiplied together give us the required number.

Example: The product prime numbers 2, 3, and 5 is 30.

Prime factorization of $30 = 2 \times 3 \times 5$

Recommended Games

Prime Factorization Definition

Prime factorization can be defined as a way of expressing a given number as the product of its prime factors. 

If a prime number occurs more than once, we write it using exponents.

Example: Prime factorization of $18 = 2\times3\times3 = 2\times3^{2}$

Recommended Worksheets

More Worksheets

A factor of a number is a number that divides the given number exactly, leaving no remainder.

Prime numbers are numbers that have only two factors, 1 and the number itself. Examples of prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, and so on.

Consider an example. The numbers 1, 2, 3, 6 are factors of the number 6.

Thus, we can say that 2 and 3 are the prime factors of 6 and express 6 as 

$6 = 2\times3$

Here, we expressed 6 as the product of its prime factors. When we write a number as a product of all its prime factors, it is called prime factorization. 

The most common methods that are used for prime factorization are:

• Prime Factorization by Factor tree method
• Prime Factorization by Division method

We will discuss these methods in detail. However, we can also find prime factors of a number by simply breaking down the number using its factors until we get prime numbers. 

Example: Find prime factorization of 48.

$42 = 8\times6$

$42 = (2\times2\times2)\times(2\times3)$

$42 = 2^{4}\times3$

Prime Factorization Methods

You can find the prime factorization of a number using various methods.

Let’s discuss the two important methods to solve prime factorization problems.

• Factor tree method
• Division method

Let us look at both the methods in detail.

Factor Tree Method

In the factor tree method, we first break down the number using the smallest prime factor of the number. The composite factors obtained in the process are further broken down until we reach the prime factors. 

The factors of the given number written in this way look like a tree. The prime numbers obtained in the end are called leaf nodes of the factor tree.

Example: Find the prime factorization of 250 using the factor tree method.

Step 1: Place the number 250 on top of the factor tree.

Step 2: Break down the given number using its smallest prime factor.

Here, $250 = 2 \times 125$

Step 3: Factorize the composite factor obtained in step 2. 

$125 = 5 \times 5$

Repeat the same step until we get all prime factors in the end. 

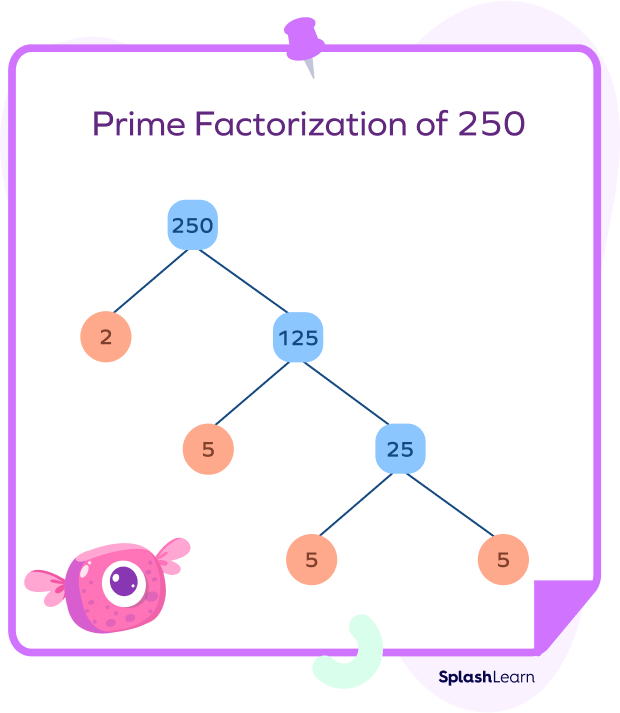
Thus, prime factorization of $250 = 2 \times 5^{3}$

Division Method

Step 1: Divide the given number by its smallest prime factor. 

Step 2: Divide the quotient obtained by its smallest prime factor.

Step 3: Repeat the process until the quotient becomes 1.

Step 4: Multiply all the prime factors.

Example: Prime factorization of 28 using division method.

Why Find Prime Factors?

As we already know that a prime number can only be divided by 1 or the number itself, so it cannot be factored any further. A composite number can be broken down using prime numbers and can be written uniquely as a product of its prime factors.

The prime numbers are the basic building blocks of any number.

We have many real-life uses of this concept while dealing with large numbers, such as in cryptography.

What Are the Applications of Prime Factorization?

• Finding square roots of perfect squares

It’s very easy to find square roots of perfect squares using prime factorization. 

Consider an example.

Prime factorization of $1225 = 5\times5\times7\times7$

$\sqrt{1225} = \sqrt{5\times5\times7\times7}$

$\sqrt{1225} = 5\times7$

$\sqrt{1225} = 35$

• Encryption or cryptography 
• Finding HCF and LCM using prime factorization
• Mental arithmetic
• Studying patterns

Finding HCF and LCM Using Prime Factorization

HCF (Highest Common Factor): The largest number of all the common factors of two numbers.

LCM (Least Common Multiple): The smallest number of all the common multiples of two numbers.

The HCF and LCM of two numbers can be calculated using the prime factorization method. It is quite useful when dealing with two or more large numbers. 

• First find the prime factorization of both the numbers. 
• HCF is the product of the smallest power of each common prime factor.
• LCM is the product of the greatest power of each prime factor.

Let us understand these points with the help of an example.

Example 1: Find the HCF and LCM of 42, 72, and 120 using prime factorization.

We will first find the prime factorization of the given numbers.

$42 = 2 \times 3 \times 7$

$72 = 2^{3} \times 3^{2}$

$120 = 2^{3} \times 3 \times 5$

HCF $=$ Product of the common prime factors with the lowest degree. 

HCF (42, 72, 120) $= 2 \times 3 = 6$

LCM = Product of the greatest powers of all prime factors.

LCM (42, 72, 120) $= 2^{3} \times 3^{2} \times 5 \times 7 = 2520$

Example 2: What is the HCF and LCM of 50 and 75?

The prime factorization of $50 = 2 \times 5^{2}$

The prime factorization of $75 = 3 × 5^{2}$

Multiply all the common prime factors with the lowest degree (power).

Here, we have only 5 as a common prime factor with the lowest power of 2.

Hence, HCF of (50, 75)$ = 5^{2} = 25$

LCM = Product of the greatest power of each prime factor.

Multiply all the prime factors with the highest degree.

Hence, LCM of (50, 75) $= 2^{1} \times  3^{1} \times 5^{2} = 150$

Prime Factorization of a Number

Take a look at the table showing prime factorization of some numbers.

Facts about Prime Factorization

• Cryptography is a branch of computer science that deals with methods of protecting important information using codes. Prime factorization plays an important role for the people who create a unique code, or encrypt the information using numbers that are not too heavy for computers to store and process quickly.
• 2 is the smallest even prime number. 2 is the only prime number that is even.
• 2 and 3 are the only consecutive prime numbers.
• 0 and 1 are neither prime nor composite.
• The only prime number that ends in 5 is 5.
• There is no largest prime number. The largest known prime number (as of February 2023) is $2^{82,589,933} \;−\; 1$, a number that has 24,862,048 digits when written in base 10. By the time you read this, it may be even larger.
• Mersenne prime: Prime number of the form $2^{n} \;−\; 1$, where n is a natural number.

In this article, we learned about factors, prime factors, prime factorization, methods of prime factorization, and how to find HCF and LCM using prime factorization. Let’s solve a few examples and practice problems for better understanding and revision!

1. Find the prime factorization of 24 using the factor tree method.

Let us look at the steps to find the prime factorization of 24 using the factor tree method:

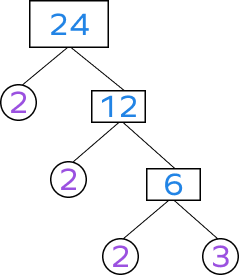
Therefore, the prime factorization of $24 = 2^{3} \times 3$.

2. Find the prime factorization of 42 using the division method.

Solution: 

Divide 42 by its smallest prime factor. Next, divide the quotient by its smallest prime factor. Repeat this process until we get 1 as a quotient.

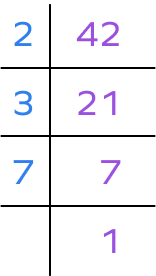
Prime factorization = Product of all prime factors

Therefore, the prime factorization of $42 = 2 \times 3 \times 7$.

3. Find the HCF of 100 and 250 using prime factorization.

To find the HCF of any number using prime factorization, we first need to find the prime factorization of both the numbers.

Prime factorization of $100 = 2^{2} \times 5^{2}$

Prime factorization of $250 = 2^{1} \times 5^{3}$

HCF (100, 250) $= 2^{1}\times 5^{2}$

Therefore, the Highest Common Factor of 100 and $250 = 50$. 

4. Find the LCM of 100 and 250 using prime factorization.

To find the LCM of any number using prime factorization, we first need to find the prime factorization of both the numbers.

LCM(100, 250) $= 2^{2} \times 5^{3}$

Therefore, the LCM of 100 and $250 = 2^{2} \times 5^{3} = 500$.

5. Write all the prime factors of 1250 using the division method.

To find the prime factors of a number, we need to find the prime factorization using one of the two methods.

Let us solve this by the division method.

Now, $\frac{1250}{2} = 625$

          $\frac{625}{5} = 125$

          $\frac{125}{5} = 25$

           $\frac{25}{5} = 5$

           $\frac{5}{5} = 1$

The prime factors of 1250 are 2 and 5. 

The prime factorization is $2 \times 5^{4}$.

Attend this quiz & Test your knowledge.

What is the prime factorization of 48?

What is the prime factorization of 15, what is the hcf of 120 and 150 using prime factorization, prime factorization is a way of expressing a given number as the ____ of its prime factors., what are the prime factors of 1000.

Is 1 a prime number?

1 is neither prime nor composite.

Is 0 prime or composite?

0 is neither prime nor composite.

How many factors does a prime number have?

Only two factors, 1 and the number itself.

Is the prime factorization of a number unique?

Yes. There is only one set of prime numbers for every whole number whose product results in the given whole number.

RELATED POSTS

• Associative Property of Multiplication – Definition With Examples
• Parentheses – Definition With Examples
• Volume of Cuboid – Definition, Formula, Derivation, Examples, FAQs
• Surface Area of Triangular Pyramid
• Power of a Power Rule: Definition, Rules, Examples, Facts, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Prime Factorization

Prime factorization is a way of expressing a number as a product of its prime factors . A prime number is a number that has exactly two factors, 1 and the number itself. For example, if we take the number 30. We know that 30 = 5 × 6, but 6 is not a prime number. The number 6 can further be factorized as 2 × 3, where 2 and 3 are prime numbers. Therefore, the prime factorization of 30 = 2 × 3 × 5, where all the factors are prime numbers.

Let us learn more about prime factorization with various mathematical problems followed by solved examples and practice questions.

What is Prime Factorization?

Prime factorization is the process of writing a number as the product of prime numbers. Prime numbers are the numbers that have only two factors, 1 and the number itself. For example, 2, 3, 5, 7, 11, 13, 17, 19, and so on are prime numbers. Prime factorization of any number means to represent that number as a product of prime numbers. For example, the prime factorization of 40 can be done in the following way:

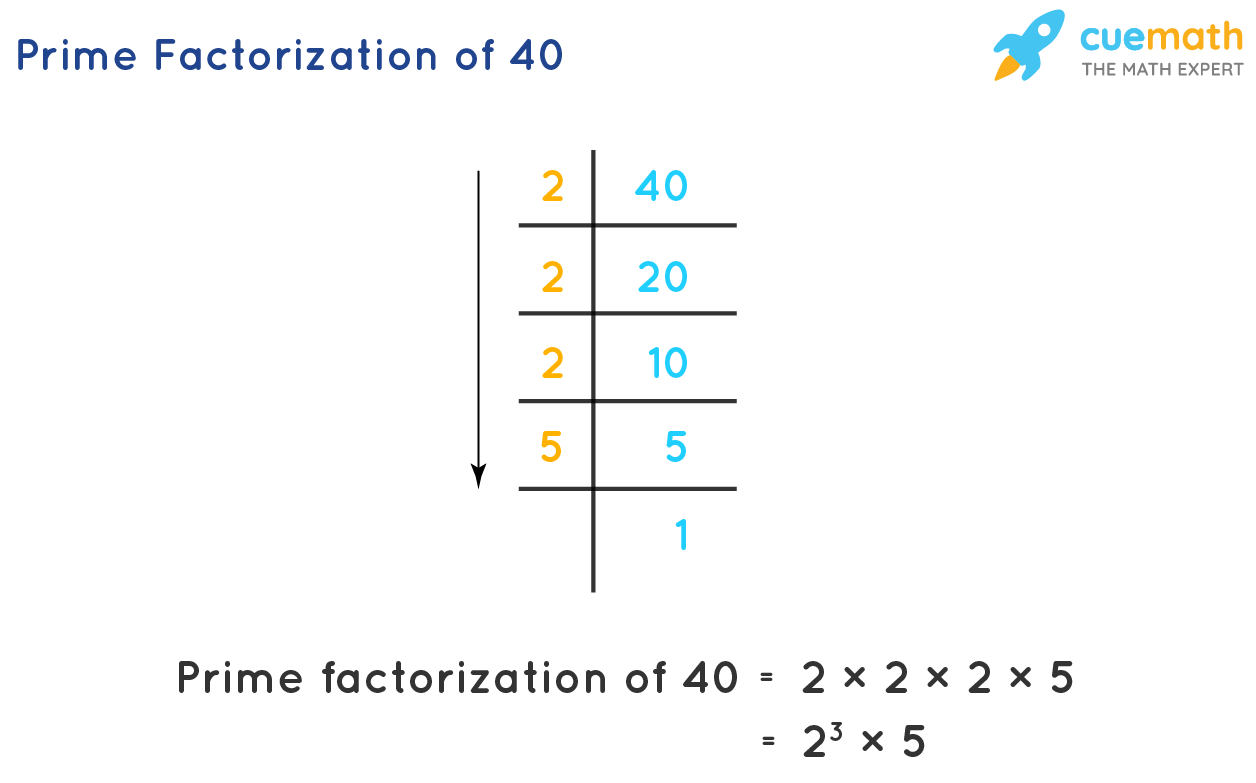
Prime Factorization Meaning

The method of breaking down a number into its prime numbers that help in forming the number when multiplied is called prime factorization. In other words, when prime numbers are multiplied to obtain the original number, it is defined as the prime factorization of the number.

Prime Factorization of a Number

Let us see the prime factorization chart of a few numbers in the table given below:

What are Prime Factors?

The prime factors of a number are the 'prime numbers' that are multiplied to get the original number. For example, 2 and 5 are the prime factors of 20, i.e., 2 × 2 × 5 = 20. We know that the factors of a number are the numbers that are multiplied to get the original number. For example, 4 and 5 are the factors of 20, i.e., 4 × 5 = 20. Therefore, it should be noted that all the factors of a number may not necessarily be prime factors.

Prime factorization is similar to factoring a number but it considers only prime numbers (2, 3, 5, 7, 11, 13, 17, 19, and so on) as its factors. Therefore, it can be said that factors that divide the original number completely and cannot be split into more factors are known as the prime factors of the given number.

Methods of Prime Factorization

There are various methods for the prime factorization of a number. The most common methods that are used for prime factorization are given below:

• Prime factorization by factor tree method
• Prime factorization by division method

Prime Factorization by Factor Tree Method

In the factor tree method, the factors of a number are found and then those numbers are further factorized until we reach the prime numbers. Let us understand the prime factorization of a number using the factor tree method with the help of the following example.

Example: Do the prime factorization of 850 using the factor tree.

Solution: Let us get the prime factors of 850 using the factor tree given below.

• Step 1: Place the number, 850, on top of the factor tree.
• Step 2: Then, write down the corresponding pair of factors as the branches of the tree. Here, they are 25 and 34.
• Step 3: Factorize the composite factors that are found in step 2, and write down the pair of factors as the next branches of the tree. Here, 25 can be further factorized into 5 × 5, and 34 can be factorized into 17 × 2
• Step 4: Repeat step 3, until we get the prime factors of all the composite factors. So, we get the prime factors of 850 = 2 × 5 2 × 17

Prime Factorization by Division Method

The division method can also be used to find the prime factors of a large number by dividing the number by prime numbers. Let us learn how to find the prime factors of a number by the division method using the following example.

Example: Do the prime factorization of 60 with the division method.

• Step 1: Divide the number by the smallest prime number such that the smallest prime number should divide the number completely. Here we divide 60 by 2 to get 30.
• Step 2: Again, divide the quotient of step 1 by the smallest prime number. So, 30 is again divided by 2 and we get 15.
• Step 3: Repeat step 2, until the quotient becomes 1. Now, 15 is not divisible by 2, so we take the next prime number which is 3. And 15 ÷ 3 = 5. Then we divide 5 ÷ 5 = 1. Since we get 1 as the quotient, we stop here.
• Step 4: Finally, multiply all the prime factors that are the divisors . Prime factorization of 60 = 2 × 2 × 3 × 5

Therefore, the prime factors of 60 are 2, 3, and 5.

Applications of Prime Factorization

Prime factorization is used extensively in the real world. The two most important applications of prime factorization are given below.

Cryptography and Prime Factorization

Hcf and lcm using prime factorization.

Cryptography is a method of protecting information using codes. Prime factorization plays an important role for the coders who create a unique code using numbers which is not too heavy for computers to store or process quickly.

To find the Highest Common Factor (HCF) and the Least Common Multiple (LCM) of two numbers, we use the prime factorization method. For this, we first do the prime factorization of both the numbers. The following points related to HCF and LCM need to be kept in mind:

• HCF is the product of the common prime factors with the smallest powers.
• LCM is the product of the common prime factors with the highest powers

Example: What is the HCF and LCM of 850 and 680?

Solution: We will first do the prime factorization of both the numbers.

• The prime factorization of 850 is: 850 = 2 1 × 5 2 × 17 1
• The prime factorization of 680 is: 680 = 2 3 × 5 1 × 17 1
• Observing this, we can see that the common prime factors of 850 and 680 with the smallest powers are 2 1 , 5 1 and 17 1 , and the common prime factors with the highest powers are 2 3 , 5 2 , 17 1
• HCF is the product of the common prime factors with the smallest powers. Hence, HCF of (850, 680) = 2 1 × 5 1 × 17 1 = 170
• LCM is the product of the common prime factors with the highest powers. Hence, LCM of (850, 680) = 2 3 × 5 2 × 17 1 = 3400
• Thus, HCF of (850, 680) = 170, LCM of (850, 680) = 3400

☛ Related Articles

• Prime Factorization of 60
• Prime Factorization of 36
• Prime Factorization of 30
• Prime Factorization of 64
• Prime Factorization of 45
• Prime Factorization of 50
• Prime Factorization of 48
• Prime Factorization of 40
• Prime Factorization of 8
• Prime Factorization of 24
• Prime Factorization of 12
• Prime Factorization of 72
• Prime Factorization of 18
• Prime Factorization of 42

Prime Factorization Examples

Example 1: Express 1080 as the product of prime factors.

We will do the prime factorization of 1080 as follows:

Thus, 1080 = 2 3 × 3 3 × 5

Therefore, the prime factorization of 1080 is 2 3 × 3 3 × 5

Example 2: Find the lowest common multiple of 48 and 72 using prime factorization.

We will do the prime factorization of 48 and 72 as shown below:

The prime factorization of 72 is shown below:

So, the prime factors of 48 = 2 4 × 3 1

the prime factors of 72 = 2 3 × 3 2

Observing this we can see that the common prime factors of 48 and 72 with the greatest powers are 2 4 , 3 2

The LCM of any 2 numbers is the product of the common prime factors with the greatest powers. Hence, LCM (48, 72) = 2 4 × 3 2 = 144

Therefore, LCM (48, 72) = 2 4 × 3 2 = 144

Example 3: Show the prime factorization of 40 using the division method and the factor tree method.

Let us use the division method and the factor tree method to prove that the prime factorization of 40 will always remain the same.

Therefore, this shows that by any method of factorization, the prime factorization remains the same. The prime factorization for a number is unique.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Prime Factorization

go to slide go to slide

FAQs on Prime Factorization

What is prime factorization in math.

Prime factorization of any number means to represent that number as a product of prime numbers. A prime number is a number that has exactly two factors, 1 and the number itself. For example, the prime factorization of 18 = 2 × 3 × 3. Here 2 and 3 are the prime factors of 18.

How to do Prime Factorization?

Prime factorization of any number can be done by using two methods:

• Division method - In this method, the given number is divided by the smallest prime number which divides it completely. After this, the quotient is again divided by the smallest prime number. This step is repeated until the quotient becomes 1. Then, all the prime factors that are divisors are multiplied.
• Factor tree method - In this method, the given number is placed on top of the factor tree. Then, the corresponding pairs of factors are written as the branches of the tree. After this step, the composite factors are again factorized and written down as the next branches. This procedure is repeated until we get the prime factors of all the composite factors. A detailed explanation of both these methods, with examples, is given above on this page.

What are Prime Factors of a Number?

The prime factors of a number are the 'prime numbers' that are multiplied to get the original number. For example, 2 and 3 are the prime factors of 12, i.e., 2 × 2 × 3 = 12. It can also be said that factors that divide the original number completely and cannot be split further into more factors are known as the prime factors of the given number. It should be noted that 4 and 6 are also factors of 12 but they are not prime numbers, therefore, we do not write them as prime factors of 12.

What is the Prime Factorization of 72, 36, and 45?

Prime factorization is the way of writing a number as the multiple of their prime factors. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, and so on. The prime factorization of 72, 36, and 45 are shown below.

• Prime factorization of 72 = 2 3 × 3 2
• Prime factorization of 36 = 2 2 × 3 2
• Prime factorization of 45 = 3 2 × 5

How to Find LCM using Prime Factorization?

The abbreviation LCM stands for 'Least Common Multiple'. The Least Common Multiple (LCM ) of a number is the smallest number that is the product of two or more numbers. The LCM of two numbers can be calculated by first finding out the prime factors of the numbers. The LCM is the product of the common prime factors with the greatest powers. For example, let us find the LCM of 12 and 18. The prime factorization of 12 = 2 2 × 3 1 , and the prime factorization of 18 = 2 1 × 3 2 . Among the common prime factors, the product of the factors with the highest powers is 2 2 × 3 2 = 36.

How to Find HCF using Prime Factorization?

The abbreviation HCF stands for 'Highest Common Factor'. The Highest Common Factor (HCF) of two numbers is the highest possible number which divides both the numbers completely. The HCF of two numbers can be found out by first finding out the prime factors of the numbers. The HCF is the product of the common prime factors with the smallest powers. For example, let us find the HCF of 12 and 18. The prime factorization of 12 = 2 2 × 3 1 , and the prime factorization of 18 = 2 1 × 3 2 . Among the common prime factors, the product of the factors with the smallest powers is 2 1 × 3 1 = 6.

Why is Prime Factorization Important?

Prime factorization is used to find the HCF and LCM of numbers. It is widely used in cryptography which is the method of protecting information using codes. Prime numbers are used to form or decode those codes.

What is the Prime Factorization of 24?

The number 24 can be written as 4 × 6. Now the composite numbers 4 and 6 can be further factorized as 4 = 2 × 2 and 6 = 2 × 3. Therefore, the prime factorization of 24 is 24 = 2 × 2 × 2 × 3 = 2 3 × 3

How is Prime Factorization used in the Real World?

Prime factorization is used extensively in the real world. For example, if we need to divide anything into equal parts, or we need to exchange money, or calculate the time while travelling, we use prime factorization. One common example is, if we have 21 candies and we need to divide it among 3 kids, we know the factors of 21 as, 21 = 3 × 7. This means we can distribute 7 candies to each kid.

When to use Prime Factorization?

Prime factorization is one of the methods used to find the Greatest Common Factor (GCF) of a given set of numbers. GCF by prime factorization is useful for larger numbers for which listing all the factors is time-consuming.

How to Find Prime Factors of a Number?

The prime factors of a number can be listed using various methods. It should be noted that prime factors are different from factors because prime factors are prime numbers that are multiplied to get the original number. One of the methods to find the prime factors of a number is the division method. Let us use this method to find the prime factors of 24.

• In this method, the given number is divided by the smallest prime number which divides it completely. So, 24 ÷ 2 = 12.
• After this, the quotient is again divided by the smallest prime number. So 12 ÷ 2 = 6.
• This step is repeated until the quotient becomes 1. This means 6 ÷ 2 = 3. Now 3 cannot be further divided or factorized because it is a prime number.
• Then, all the prime factors that are divisors are multiplied and listed.
• So we get 24 = 2 × 2 × 2 × 3 and we know that the prime factors of 24 are 2 and 3 and the prime factorization of 24 = 2 3 × 3

What is the Definition of Prime Factorization?

Prime factorization is defined as the way of expressing a number as a product of its prime factors. We know that a prime number is a number that has exactly two factors, 1 and the number itself. For example, if we take the number 20. We know that 20 = 5 × 4, but 4 is not a prime number. The number 4 can further be factorized as 2 × 2, where 2 is a prime number. Therefore, the prime factorization of 20 = 2 × 2 × 5, where all the factors are prime numbers.

Product of Primes, LCM, HCF Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Prime factorization using a factor tree

Once you get to the primes in your "tree", they are the "leaves", and you stop factoring in that “branch”. So 24 = 2 × 2 × 2 × 3. This is the prime factorization of 24.

 Examples:

72 has lots of factors so the factoring takes many steps.

72 = 2 × 2 × 2 × 3 × 3

We could have also started by writing 72 = 2 × 36 or 72 = 4 ×18.

1. Factor the following numbers to their prime factors.

2. Factor the following numbers to their prime factors.

By using the process above (building numbers starting from primes) you can build ANY whole number there is! Can you believe that?

We can say this in another way: ALL numbers can be factored so the factors are prime numbers. That is sort of amazing! This fact is known as the fundamental theorem of arithmetic . Indeed, it is fundamental.

See 992 factored on the right. 992 = 2 × 2 × 2 × 2 × 2 × 31. For 83,283 we get 3 × 17 × 23 × 71, and 151,282 = 2 × 3 × 3 × 3 × 11 × 11 × 23.

3. Build numbers from primes.

4. Build more numbers from primes.

5. Try it on your own! Pick 3-6 primes as you wish (you can use the same prime     several times), and see what number is built from them. 

• Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
• Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
• Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
• Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
• Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Two-step without parentheses
• Two-step with parentheses
• Three/four steps without parentheses
• Three/four steps with parentheses
• Multi-step without parentheses
• Multi-step with parentheses
• Prime Factorization
• Negative Factors
• Positive Factors
• Odd Factors
• Even Factors
• Biggest Factor
• Equivalent Fractions
• Add, Subtract
• Add, Subtract Like Denominators
• Add, Subtract Unlike Denominators
• Multiply with Whole Number
• Divide with Whole Number
• Mixed Numbers
• Complex Fractions
• Improper Fractions
• Negative Reciprocal
• Long Addition
• Long Subtraction
• Long Multiplication
• Long Division
• Long Division with Remainder
• Add/Subtract
• Multiplication
• Decimal to Fraction
• Fraction to Decimal
• Negative Exponent
• Square Root
• Ratios & Proportions

Number Line

• Expanded Form
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions
• prime\:factors\:of\:45
• prime\:factors\:of\:15
• prime\:factors\:of\:28
• prime\:factors\:of\:32

prime-factorization-calculator

• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

• Maths Notes Class 10
• NCERT Solutions Class 10
• RD Sharma Solutions Class 10
• Maths Formulas Class 10
• Class 10 Syllabus
• Class 10 Revision Notes
• Physics Notes Class 10
• Chemistry Notes Class 10
• Biology Notes Class 10
• History Notes class 10
• political science class 10
• Geography Notes class 10
• Social science Notes class 10

Prime Factorization

Prime Factorization is a way of writing numbers as the product of prime numbers. Prime numbers are natural numbers that have only two divisors, 1 and themselves. Prime Factorization involves only the prime numbers as every composite number can be written as the product of primes.

Let’s understand the Prime Factorization with the following illustration:

More Examples of Prime Factorization:

12 can be written as 2 x 6 6 can be further factorized as 2 x 3. So 12 can be rewritten as 2 x 2 x 3 No more factorization possible as 2 and 3 cannot be divide further, so 2 x 2 x 3 is our prime factorization 54 can written as 2 x 27. 27 can be further factorized as 3 x 9. So we rewrite 54 as 2 x 3 x 9 9 can be further factorized as 3 x 3. So we rewrite 54 as 2 x 3 x 3 x 3. No more factorization possible, so 2 x 3 x 3 x 3 is our prime factorization

In this article, we will learn about what is prime factorization, its examples, and methods in detail.

Table of Content

Prime Factorization Meaning

What are prime factors, prime factorization methods, prime factorization by division method, prime factorization of numbers, finding hcf and lcm by prime factorization, applications of prime factorization in real life, prime factorization solved examples.

Prime factorization is the method of identifying the prime factors of a number. Since composite numbers have more than two factors, this method is applicable exclusively to them and not to prime numbers, which only have two distinct positive divisors: 1 and the number itself​.

Prime factors are the prime numbers that divide a given number exactly without leaving a remainder. In other words, they are the building blocks of a number.

When a number is expressed as a product of its prime factors, it is said to be in its prime factorization form.

Some examples of prime factors are:

• 2 and 3 are the prime factors of 12, as 12 = 2 2 × 3,
• 3 and 5 are the prime factors of 15, as 15 = 3 × 5,
• 2 and 7 are the prime factors of 14,  as 15 = 3 × 5.

Two common methods of Prime Factorization are:

• Division Method
• Factor Tree Method

In this method, the number is successively divided by prime numbers until the quotient becomes 1 , with each division identifying a prime factor.

Steps to identify the prime factors of a number by Division Method :

Step 1: Divide the number by the smallest prime number (i.e. 2) until we are able to divide the given number without leaving any remainder. Step 2: Move on to the next prime number and repeat the division until the quotient becomes 1. Step 3: The prime factors are the divisors used in the division process.

Let’s consider some examples for better understanding.

Examples of Prime Factorization by Division Method

Example 1: Find the Prime Factorization of 60 using Division Method.

Example 2: Find the Prime Factorization of 210 using Division Method.

Example 3: Express 56 as the product of its Prime Factors.

Prime Factorization by Factor Tree Method

The Factor Tree Method involves breaking down a number into its prime factors by constructing a tree-like structure called a factor tree.

Steps to identify the prime factors of a number by Factor Tree Method:

Step 1: Identify two factors of the number that are not prime. Step 2: Write these two factors as branches of the factor tree. Step 3: Repeat steps 1 and 2 for each non-prime factor until all branches end with prime numbers. Step 4: The prime factors are the numbers at the end of the branches.

Let’s consider some examples for better understanding as follows:

Examples of Prime Factorization by Factor Tree Method

Example 1: Find the factorization of 60 by the Factor Tree Method.

Example 2: Make the Factor Tree of 210.

Please refer Prime Factorization Tips and Tricks to Improve your time in finding prime factorization.

Some examples of prime factorization are listed below:

HCF and LCM can be easily calculated by the method of prime factorization:

Finding HCF

For the HCF, take the lowest power of each common prime factor from both numbers.

For Example:

• Common prime factors: 2 and 3
• For 2: min⁡(2,4) = 2
• For 3: min⁡(1,1) = 1

So, the HCF is:

HCF = 2 2 x 3 1 = 4 x 3 = 12

Finding LCM

For the LCM, take the highest power of each prime factor present in either number.

• Prime Factors: 2,3 and 5
• For 2: max⁡(2,4) = 4
• For 3: max⁡(1,1) = 1
• For 5: max⁡(1,0) = 1

So, the LCM is:

LCM = 2 4 × 3 1 × 5 1 = 16 × 3 × 5 = 240

• Finding HCF and LCM : Prime factorization helps determine the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of numbers, essential for simplifying fractions and finding common denominators.
• Cryptography : It is crucial in public key cryptography, such as RSA, where the difficulty of factoring large composite numbers ensures secure communication.
• Simplifying Fractions : By factoring numerators and denominators into prime factors, common factors can be canceled out, simplifying fractions effectively.
• Divisibility Rules : Prime factorization aids in applying divisibility rules, quickly indicating whether one number is divisible by another.
• Data Compression : Techniques based on prime factorization can optimize data storage and transmission in computer science, enhancing efficiency.
• Network Security : Algorithms based on prime factorization enhance data security during network transfers, protecting sensitive information.

Read in Detail: Real Life Applications of Prime Factorization

Let’s solve some questions on Prime Factorisation.

Problem 1: What is the Prime Factorisation of 80?

To find the prime factorization of 80, we can start by dividing it by the smallest prime number, which is 2. 80 divided by 2 equals 40. 40 divided by 2 equals 20. 20 divided by 2 equals 10. 10 divided by 2 equals 5. Now, since 5 is a prime number, we can stop dividing. Therefore, the prime factorization of 80 is: 2 × 2 × 2 × 2 × 5.

Problem 2: Prime factorization of 120.

Starting with the smallest prime number, which is 2. 120 divided by 2 equals 60. 60 divided by 2 equals 30. 30 divided by 2 equals 15. Now, since 15 is not divisible by 2, we move on to the next prime number (i.e, 3) 15 divided by 3 equals 5. Now, since 5 is a prime number, we can stop dividing. Therefore, the prime factorization of 120 is: 2 × 2 × 2 × 3 × 5

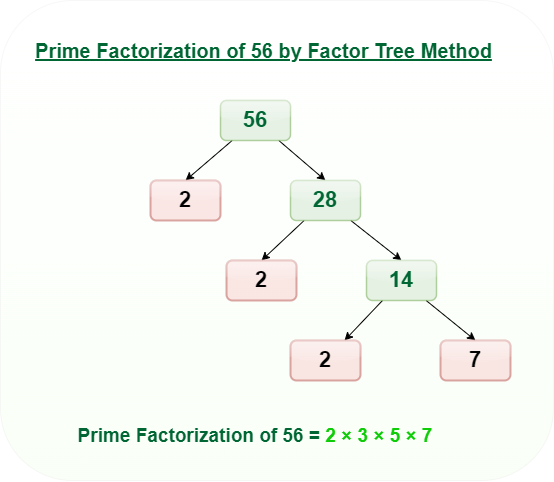
Problem 3: What is the Factor Tree of 56?

Related Articles:

Interesting Facts about Prime Numbers Factorization of Algebraic Expression Composite Numbers

Prime Factorization Worksheet

1. Find the prime factorization of 36.

2. Determine the prime factorization of 90.

3. What is the prime factorization of 48?

4. Find the prime factorization of 105.

5. What is the prime factorization of 84?

6. Determine the prime factorization of 100.

7. Find the prime factorization of 2310.

8. What is the prime factorization of 56?

9. Determine the prime factorization of 150.

10. What is the prime factorization of 1250?

• 36: [Tex]2^2 \times 3^2[/Tex]
• 90: [Tex]2 \times 3^2 \times 5[/Tex]
• 48: [Tex]2^4 \times 3[/Tex]
• 105: [Tex]3 \times 5 \times 7[/Tex]
• 84: [Tex]2^2 \times 3 \times 7[/Tex]
• 100: [Tex]2^2 \times 5^2[/Tex]
• 2310: [Tex]2 \times 3 \times 5 \times 7 \times 11[/Tex]
• 56: [Tex]2^3 \times 7[/Tex]
• 150: [Tex]2 \times 3 \times 5^2[/Tex]
• 1250: [Tex]2 \times 5^4[/Tex]

Prime factorization is a fundamental concept in mathematics that involves expressing a number as a product of its prime factors. This technique is not only essential for simplifying mathematical expressions but also plays a crucial role in various fields, including number theory, cryptography, and computational mathematics. In summary, prime factorization is a vital mathematical tool that underpins many concepts and applications. Its significance extends beyond pure mathematics into practical applications in technology and everyday life.

FAQs on Prime Factorization

What is prime factorization.

A method to decompose any given number into its constituent prime number is called prime factorization.

Define Prime Factors of a Number.

In Prime Factorization, the prime consitituents of the number are called prime factors of that given number. For example, 2 and 3 are the prime factors of 24 as 24 = 2 3 × 3.

How To Find Prime Factors of a Number?

To find the prime factors of a number, you can use the method of trial division. Start dividing the number by the smallest prime number i.e., 2 and continue dividing by prime numbers until the quotient becomes 1. The divisors you used are the prime factors.

Can a Number have More than One Prime Factorization?

No, a number has a unique prime factorization. This is known as the Fundamental Theorem of Arithmetic. Regardless of the order in which the factors are written, the prime factors of a number remain the same.

What is Difference between Prime and Composite Factors?

Prime factors are the prime numbers that divide a given number without leaving a remainder, while composite factors are the composite numbers (non-prime numbers) that divide a given number without leaving a remainder.

How To Find LCM using Prime Factorization?

To find the least common multiple (LCM), you consider all the prime factors and take the highest exponent for each prime factor.

How To Find HCF by Prime Factorization Method?

To find the HCF of two or more numbers, you identify the common prime factors and take the smallest exponent for each prime factor.

What are Prime Factors of 32?

The prime factors of 32 are 2 raised to the power of 5 (2 5 ).

What are Prime Factors of 45?

The prime factors of 45 are 3 and 5, since 45 = 3 2 × 5.

What are Prime Factors of 75?

The prime factors of 75 are 3 and 5.

How To Find Prime Factors of a Large Number?

To find the prime factors of a large number: Start with the smallest prime number, 2. Divide the large number by 2. If it’s divisible, 2 is a prime factor; divide as many times as possible until it’s no longer divisible by 2. Move to the next prime numbers (3, 5, 7, 11, …) and repeat the process for each: divide the number by the prime number, and if it’s divisible, that prime is a factor. Continue dividing by that prime until it’s no longer divisible. Continue the process with increasing prime numbers until the number you’re dividing by is greater than the square root of the original number. At that point, if the number you’re left with is greater than 1, it’s also a prime factor.

Similar Reads

• Mathematics
• School Learning
• Maths-Class-10

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?

2.5 Prime Factorization and the Least Common Multiple

Learning objectives.

By the end of this section, you will be able to:

• Find the prime factorization of a composite number
• Find the least common multiple (LCM) of two numbers

Be Prepared 2.12

Before you get started, take this readiness quiz.

Is 810 810 divisible by 2 , 3 , 5 , 6 , or 10 ? 2 , 3 , 5 , 6 , or 10 ? If you missed this problem, review Example 2.44 .

Be Prepared 2.13

Is 127 127 prime or composite? If you missed this problem, review Example 2.47 .

Write 2 ⋅ 2 ⋅ 2 ⋅ 2 2 ⋅ 2 ⋅ 2 ⋅ 2 in exponential notation. If you missed this problem, review Example 2.5 .

Find the Prime Factorization of a Composite Number

In the previous section, we found the factors of a number. Prime numbers have only two factors, the number 1 1 and the prime number itself. Composite numbers have more than two factors, and every composite number can be written as a unique product of primes. This is called the prime factorization of a number. When we write the prime factorization of a number, we are rewriting the number as a product of primes. Finding the prime factorization of a composite number will help you later in this course.

Prime Factorization

The prime factorization of a number is the product of prime numbers that equals the number.

Manipulative Mathematics

You may want to refer to the following list of prime numbers less than 50 50 as you work through this section.

Prime Factorization Using the Factor Tree Method

One way to find the prime factorization of a number is to make a factor tree . We start by writing the number, and then writing it as the product of two factors. We write the factors below the number and connect them to the number with a small line segment—a “branch” of the factor tree.

If a factor is prime, we circle it (like a bud on a tree), and do not factor that “branch” any further. If a factor is not prime, we repeat this process, writing it as the product of two factors and adding new branches to the tree.

We continue until all the branches end with a prime. When the factor tree is complete, the circled primes give us the prime factorization.

For example, let’s find the prime factorization of 36 . 36 . We can start with any factor pair such as 3 3 and 12 . 12 . We write 3 3 and 12 12 below 36 36 with branches connecting them.

The factor 3 3 is prime, so we circle it. The factor 12 12 is composite, so we need to find its factors. Let’s use 3 3 and 4 . 4 . We write these factors on the tree under the 12 . 12 .

The factor 3 3 is prime, so we circle it. The factor 4 4 is composite, and it factors into 2 · 2 . 2 · 2 . We write these factors under the 4 . 4 . Since 2 2 is prime, we circle both 2 s . 2 s .

The prime factorization is the product of the circled primes. We generally write the prime factorization in order from least to greatest.

In cases like this, where some of the prime factors are repeated, we can write prime factorization in exponential form.

Note that we could have started our factor tree with any factor pair of 36 . 36 . We chose 12 12 and 3 , 3 , but the same result would have been the same if we had started with 2 2 and 18 , 4 18 , 4 and 9 , or 6 and 6 . 9 , or 6 and 6 .

Find the prime factorization of a composite number using the tree method.

• Step 1. Find any factor pair of the given number, and use these numbers to create two branches.
• Step 2. If a factor is prime, that branch is complete. Circle the prime.
• Step 3. If a factor is not prime, write it as the product of a factor pair and continue the process.
• Step 4. Write the composite number as the product of all the circled primes.

Example 2.48

Find the prime factorization of 48 48 using the factor tree method.

Check this on your own by multiplying all the factors together. The result should be 48 . 48 .

Try It 2.95

Find the prime factorization using the factor tree method: 80 80

Try It 2.96

Find the prime factorization using the factor tree method: 60 60

Example 2.49

Find the prime factorization of 84 using the factor tree method.

Draw a factor tree of 84 . 84 .

Try It 2.97

Find the prime factorization using the factor tree method: 126 126

Try It 2.98

Find the prime factorization using the factor tree method: 294 294

Prime Factorization Using the Ladder Method

The ladder method is another way to find the prime factors of a composite number. It leads to the same result as the factor tree method. Some people prefer the ladder method to the factor tree method, and vice versa.

To begin building the “ladder,” divide the given number by its smallest prime factor. For example, to start the ladder for 36 , 36 , we divide 36 36 by 2 , 2 , the smallest prime factor of 36 . 36 .

To add a “step” to the ladder, we continue dividing by the same prime until it no longer divides evenly.

Then we divide by the next prime; so we divide 9 9 by 3 . 3 .

We continue dividing up the ladder in this way until the quotient is prime. Since the quotient, 3 , 3 , is prime, we stop here.

Do you see why the ladder method is sometimes called stacked division?

The prime factorization is the product of all the primes on the sides and top of the ladder.

Notice that the result is the same as we obtained with the factor tree method.

Find the prime factorization of a composite number using the ladder method.

• Step 1. Divide the number by the smallest prime.
• Step 2. Continue dividing by that prime until it no longer divides evenly.
• Step 3. Divide by the next prime until it no longer divides evenly.
• Step 4. Continue until the quotient is a prime.
• Step 5. Write the composite number as the product of all the primes on the sides and top of the ladder.

Example 2.50

Find the prime factorization of 120 120 using the ladder method.

Check this yourself by multiplying the factors. The result should be 120 . 120 .

Try It 2.99

Find the prime factorization using the ladder method: 80 80

Try It 2.100

Find the prime factorization using the ladder method: 60 60

Example 2.51

Find the prime factorization of 48 48 using the ladder method.

Try It 2.101

Find the prime factorization using the ladder method. 126 126

Try It 2.102

Find the prime factorization using the ladder method. 294 294

Find the Least Common Multiple (LCM) of Two Numbers

One of the reasons we look at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of 10 10 and 25 . 25 . We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.

We see that 50 50 and 100 100 appear in both lists. They are common multiples of 10 10 and 25 . 25 . We would find more common multiples if we continued the list of multiples for each.

The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of 10 10 and 25 25 is 50 . 50 .

Find the least common multiple (LCM) of two numbers by listing multiples.

• Step 1. List the first several multiples of each number.
• Step 2. Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
• Step 3. Look for the smallest number that is common to both lists.
• Step 4. This number is the LCM.

Example 2.52

Find the LCM of 15 15 and 20 20 by listing multiples.

List the first several multiples of 15 15 and of 20 . 20 . Identify the first common multiple.

15: 15 , 30 , 45 , 60 , 75 , 90 , 105 , 120 20: 20 , 40 , 60 , 80 , 100 , 120 , 140 , 160 15: 15 , 30 , 45 , 60 , 75 , 90 , 105 , 120 20: 20 , 40 , 60 , 80 , 100 , 120 , 140 , 160

The smallest number to appear on both lists is 60 , 60 , so 60 60 is the least common multiple of 15 15 and 20 . 20 .

Notice that 120 120 is on both lists, too. It is a common multiple, but it is not the least common multiple.

Try It 2.103

Find the least common multiple (LCM) of the given numbers: 9 and 12 9 and 12

Try It 2.104

Find the least common multiple (LCM) of the given numbers: 18 and 24 18 and 24

Prime Factors Method

Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of 12 12 and 18 . 18 .

We start by finding the prime factorization of each number.

Then we write each number as a product of primes, matching primes vertically when possible.

Now we bring down the primes in each column. The LCM is the product of these factors.

Notice that the prime factors of 12 12 and the prime factors of 18 18 are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that 36 36 is the least common multiple.

Find the LCM using the prime factors method.

• Step 1. Find the prime factorization of each number.
• Step 2. Write each number as a product of primes, matching primes vertically when possible.
• Step 3. Bring down the primes in each column.
• Step 4. Multiply the factors to get the LCM.

Example 2.53

Find the LCM of 15 15 and 18 18 using the prime factors method.

Try It 2.105

Find the LCM using the prime factors method. 15 and 20 15 and 20

Try It 2.106

Find the LCM using the prime factors method. 15 and 35 15 and 35

Example 2.54

Find the LCM of 50 50 and 100 100 using the prime factors method.

Try It 2.107

Find the LCM using the prime factors method: 55 , 88 55 , 88

Try It 2.108

Find the LCM using the prime factors method: 60 , 72 60 , 72

ACCESS ADDITIONAL ONLINE RESOURCES

• Ex 1: Prime Factorization
• Ex 2: Prime Factorization
• Ex 3: Prime Factorization
• Ex 1: Prime Factorization Using Stacked Division
• Ex 2: Prime Factorization Using Stacked Division
• The Least Common Multiple
• Example: Determining the Least Common Multiple Using a List of Multiples
• Example: Determining the Least Common Multiple Using Prime Factorization

Section 2.5 Exercises

Practice makes perfect.

In the following exercises, find the prime factorization of each number using the factor tree method.

In the following exercises, find the prime factorization of each number using the ladder method.

In the following exercises, find the prime factorization of each number using any method.

In the following exercises, find the least common multiple (LCM) by listing multiples.

8 , 12 8 , 12

4 , 3 4 , 3

6 , 15 6 , 15

12 , 16 12 , 16

30 , 40 30 , 40

20 , 30 20 , 30

60 , 75 60 , 75

44 , 55 44 , 55

In the following exercises, find the least common multiple (LCM) by using the prime factors method.

24 , 30 24 , 30

28 , 40 28 , 40

70 , 84 70 , 84

84 , 90 84 , 90

In the following exercises, find the least common multiple (LCM) using any method.

6 , 21 6 , 21

9 , 15 9 , 15

32 , 40 32 , 40

Everyday Math

Grocery shopping Hot dogs are sold in packages of ten, but hot dog buns come in packs of eight. What is the smallest number of hot dogs and buns that can be purchased if you want to have the same number of hot dogs and buns? (Hint: it is the LCM!)

Grocery shopping Paper plates are sold in packages of 12 12 and party cups come in packs of 8 . 8 . What is the smallest number of plates and cups you can purchase if you want to have the same number of each? (Hint: it is the LCM!)

Writing Exercises

Do you prefer to find the prime factorization of a composite number by using the factor tree method or the ladder method? Why?

Do you prefer to find the LCM by listing multiples or by using the prime factors method? Why?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Prealgebra 2e
• Publication date: Mar 11, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra-2e/pages/2-5-prime-factorization-and-the-least-common-multiple

© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Prime Factorization Calculator

Prime factorization calculator

This calculator finds the prime factorization of a given number and creates a factor tree. Also, the calculator finds all factors, all factor pairs, and can check if the number is prime or not. The calculator generates a step-by-step explanation of how the work was done.

Get Widget Code

• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

What is prime factorization?

Find the prime factorization and factor tree for 60..

Step 1: Start with any number that divides 60; for our example, we will select 10.

Step 2: Write 10 as a product of 2 and 5. $ \color{blue}{10 = 2 \cdot 5} $.

Step 3: Write 6 as a product of 2 and 3. $ 6 = 2 \cdot 3 $.

Step 4: The end nodes are the prime factors of 60.

Finding all factors

Example: Find all factors of 54.

Step 1: Begin the list with 1 and end it with 54.

Step 2: Since $ 54 = 2 \cdot 27 $ we put in 2 and 27 into an array.

Step 3: Since $ 54 = 3 \cdot 18 $ so we will put in 3 and 18 into an array.

Step 4: At the end we have $ 54 = 6 \cdot 9 $

Check if the number is prime

Example: Check whether a number 581 is prime or not.

Step 1: Find the square root of 581.

Step 2: Try to divide 581 by all prime numbers less or equal to 25.

In this example we will try to divide 581 with : 2 , 3, 5, 7, 11, 13, 17, 19 and 23.

581 is divisible by 3 so is is not prime.

1. Prime Factorization - video tutorial

2. Prime Factorization : Definition, Methods, Examples, FAQs

3. Prime Factorization test with video solutuins.

4. Print all prime factors - code in C++, C, Java, Python, C#, Javascript and PHP.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Filter year:

Prime Numbers Reasoning and Problem Solving

Once children are secure in identifying if a number is prime, it's time for them to apply their skills to some reasoning and problem-solving activities. This Year 5 Prime Numbers worksheet features six engaging questions for pupils to complete such as spotting the mistake, explaining if a statement is correct and identifying the prime number being described. Download now!

Curriculum Objectives

• Know and use the vocabulary of prime numbers, prime factors and composite (non-prime) numbers

Multiplication and Division 1

More like this

More Y5 resources