case study hypothesis testing

Probability and Statistics for Scientists and Engineers

16 hypothesis testing case study, 16.1 objectives.

Define and use properly in context all new terminology, to include: point estimate , null hypothesis , alternative hypothesis , hypothesis test , randomization , permutation test , test statistic , and \(p\) -value .

Conduct a hypothesis test using a randomization test, to include all 4 steps.

16.2 Introduction

We now have the foundation to move on to statistical modeling. First we will begin with inference, where we use the ideas of estimation and the variance of estimates to make decisions about the population. We will also briefly introduce the ideas of prediction. Then in the final block of material, we will examine some common linear models and use them for both prediction and inference.

16.3 Foundation for inference

Suppose a professor randomly splits the students in class into two groups: students on the left and students on the right. If \(\hat{p}_{_L}\) and \(\hat{p}_{_R}\) represent the proportion of students who own an Apple product on the left and right, respectively, would you be surprised if \(\hat{p}_{_L}\) did not exactly equal \(\hat{p}_{_R}\) ?

While the proportions would probably be close to each other, they are probably not exactly the same. We would probably observe a small difference due to chance .

Exercise : If we don’t think the side of the room a person sits on in class is related to whether the person owns an Apple product, what assumption are we making about the relationship between these two variables? 77

Studying randomness of this form is a key focus of statistical modeling. In this block, we’ll explore this type of randomness in the context of several applications, and we’ll learn new tools and ideas that can be applied to help make decisions from data.

16.4 Randomization case study: gender discrimination

We consider a study investigating gender discrimination in the 1970s, which is set in the context of personnel decisions within a bank. 78 The research question we hope to answer is, “Are females discriminated against in promotion decisions made by male managers?”

16.4.1 Variability within data

The participants in this study were 48 male bank supervisors attending a management institute at the University of North Carolina in 1972. They were asked to assume the role of the personnel director of a bank and were given a personnel file to judge whether the person should be promoted to a branch manager position. The files given to the participants were identical, except that half of them indicated the candidate was male and the other half indicated the candidate was female. These files were randomly assigned to the subjects.

Exercise : Is this an observational study or an experiment? How does the type of study impact what can be inferred from the results? 79

For each supervisor, we recorded the gender associated with the assigned file and the promotion decision. Using the results of the study summarized in the table below, we would like to evaluate whether females are unfairly discriminated against in promotion decisions. In this study, a smaller proportion of females are promoted than males (0.583 versus 0.875), but it is unclear whether the difference provides convincing evidence that females are unfairly discriminated against.

\[ \begin{array}{cc|ccc} & & &\textbf{Decision}\\ & & \mbox{Promoted} & \mbox{Not Promoted} & \mbox{Total} \\ & \hline \mbox{male} & 21 & 3 & 24 \\ \textbf{Gender}& \mbox{female} & 14 & 10 & 24 \\ & \mbox{Total} & 35 & 13 & 48 \\ \end{array} \]

Thought Question : Statisticians are sometimes called upon to evaluate the strength of evidence. When looking at the rates of promotion for males and females in this study, why might we be tempted to immediately conclude that females are being discriminated against?

The large difference in promotion rates (58.3% for females versus 87.5% for males) suggest there might be discrimination against women in promotion decisions. Most people come to this conclusion because they think these sample statistics are the actual population parameters. We cannot yet be sure if the observed difference represents discrimination or is just from random variability. Generally, there is fluctuation in sample data; if we conducted the experiment again, we would likely get different values. We also wouldn’t expect the sample proportions for males and females to be exactly equal, even if the truth was that the promotion decisions were independent of gender. To make a decision, we must understand the random variability and use it to compare with the observed difference.

This question is a reminder that the observed outcomes in the sample may not perfectly reflect the true relationships between variables in the underlying population. The table shows there were 7 fewer promotions in the female group than in the male group, a difference in promotion rates of 29.2% \(\left( \frac{21}{24} - \frac{14}{24} = 0.292 \right)\) . This observed difference is what we call a point estimate of the true effect. The point estimate of the difference is large, but the sample size for the study is small, making it unclear if this observed difference represents discrimination or whether it is simply due to chance. We label these two competing claims, chance or discrimination, as \(H_0\) and \(H_A\) :

\(H_0\) : Null hypothesis. The variables gender and decision are independent. They have no relationship, and the observed difference between the proportion of males and females who were promoted, 29.2%, was due to chance. \(H_A\) : Alternative hypothesis. The variables gender and decision are not independent. The difference in promotion rates of 29.2% was not due to chance, and equally qualified females are less likely to be promoted than males.

Hypothesis testing These hypotheses are part of what is called a hypothesis test . A hypothesis test is a statistical technique used to evaluate competing claims using data. Often times, the null hypothesis takes a stance of no difference or no effect and thus is skeptical of the research claim. If the null hypothesis and the data notably disagree, then we will reject the null hypothesis in favor of the alternative hypothesis.

Don’t worry if you aren’t a master of hypothesis testing at the end of this chapter. We’ll discuss these ideas and details many times throughout this block.

What would it mean if the null hypothesis, which says the variables gender and decision are unrelated, is true? It would mean each banker would decide whether to promote the candidate without regard to the gender indicated on the file. That is, the difference in the promotion percentages would be due to the way the files were randomly divided to the bankers, and the randomization just happened to give rise to a relatively large difference of 29.2%.

Consider the alternative hypothesis: bankers were influenced by which gender was listed on the personnel file. If this was true, and especially if this influence was substantial, we would expect to see some difference in the promotion rates of male and female candidates. If this gender bias was against females, we would expect a smaller fraction of promotion recommendations for female personnel files relative to the male files.

We will choose between these two competing claims by assessing if the data conflict so much with \(H_0\) that the null hypothesis cannot be deemed reasonable. If this is the case, and the data support \(H_A\) , then we will reject the notion of independence and conclude that these data provide strong evidence of discrimination. Again, we will do this by determining how much difference in promotion rates would happen by random variation and compare this with the observed difference. We will make a decision based on probability considerations.

16.4.2 Simulating the study

The table of data shows that 35 bank supervisors recommended promotion and 13 did not. Now, suppose the bankers’ decisions were independent of gender, that is the null hypothesis is true. Then, if we conducted the experiment again with a different random assignment of files, differences in promotion rates would be based only on random fluctuation. We can actually perform this randomization , which simulates what would have happened if the bankers’ decisions had been independent of gender but we had distributed the files differently. 80 We will walk through the steps next.

First let’s import the data.

Let’s inspect the data set.

Let’s look at a table of the data, showing gender versus decision .

Let’s do some categorical data cleaning. To get the tally() results to look like our initial table, we need to change the variables from characters to factors and reorder the levels. By default, factor levels are ordered alphabetically, but we want promoted and male to appear as the first levels in the table.

We will use mutate_if() to convert character variables to factors and fct_relevel() to reorder the levels.

Now that we have the data in the form that we want, we are ready to conduct the permutation test , a simulation of what would have happened if the bankers’ decisions had been independent of gender but we had distributed the files differently. To think about this simulation , imagine we actually had the personnel files. We thoroughly shuffle 48 personnel files, 24 labeled male and 24 labeled female , and deal these files into two stacks. We will deal 35 files into the first stack, which will represent the 35 supervisors who recommended promotion. The second stack will have 13 files, and it will represent the 13 supervisors who recommended against promotion. That is, we keep the same number of files in the promoted and not_promoted categories, and imagine simply shuffling the male and female labels around. Remember that the files are identical except for the listed gender. This simulation then assumes that gender is not important and, thus, we can randomly assign the files to any of the supervisors. Then, as we did with the original data, we tabulate the results and determine the fraction of male and female candidates who were promoted. Since we don’t actually physically have the files, we will do this shuffle via computer code.

Since the randomization of files in this simulation is independent of the promotion decisions, any difference in the two fractions is entirely due to chance. The following code shows the results of such a simulation.

The shuffle() function randomly rearranges the gender column while keeping the decision column the same. It is really a sampling without replacement. That is, we randomly sample 35 personnel files to be promoted and the other 13 personnel files are not_promoted .

Exercise : What is the difference in promotion rates between the two simulated groups? How does this compare to the observed difference, 29.2%, from the actual study? 81

Calculating by hand will not help in a simulation, so we must write a function or use an existing one. We will use diffprop() from the mosaic package. The code to find the difference for the original data is:

Notice that this is subtracting the proportion of males promoted from the proportion of females promoted. This does not impact our results as this is an arbitrary decision. We just need to be consistent in our analysis. If we prefer to use positive values, we can adjust the order easily.

Notice what we have done here; we developed a single value metric to measure the relationship between gender and decision . This single value metric is called the test statistic . We could have used a number of different metrics, to include just the difference in number of promoted males and females. The key idea in hypothesis testing is that once you decide on a test statistic, you need to find the distribution of that test statistic, assuming the null hypothesis is true.

16.4.3 Checking for independence

We computed one possible difference under the null hypothesis in the exercise above, which represents one difference due to chance. Repeating the simulation, we get another difference due to chance: -0.042. And another: 0.208. And so on until we repeat the simulation enough times that we have a good idea of what represents the distribution of differences from chance alone . That is, the difference if there really is no relationship between gender and the promotion decision. We are using a simulation when there is actually a finite number of permutations of the gender label. From Chapter 8 on counting, we have 48 labels of which 24 are male and 24 are female . Thus the total number of ways to arrange the labels differently is:

\[ \frac{48!}{24!\cdot24!} \approx 3.2 \cdot 10^{13} \]

As is often the case, the number of all possible permutations is too large to find by hand or even via code. Thus, we will use a simulation, a subset of all possible permutations, to approximate the permutation test. Using simulation in this way is called a randomization test .

Let’s simulate the experiment and plot the simulated values of the difference in the proportions of male and female files recommended for promotion.

In Figure 16.1 , we will insert a vertical line at the value of our observed difference.

Figure 16.1: Distribution of test statistic.

Note that the distribution of these simulated differences is centered around 0 and is roughly symmetrical. It is centered on zero because we simulated differences in a way that made no distinction between men and women. This makes sense: we should expect differences from chance alone to fall around zero with some random fluctuation for each simulation under the assumption of the null hypothesis. The histogram also looks like a normal distribution; this is not a coincidence, but a result of the Central Limit Theorem , which we will learn about later in this block.

Example : How often would you observe a difference as extreme as -29.2% (-0.292) according to the figure? (Often, sometimes, rarely, or never?)

It appears that a difference as extreme as -29.2% due to chance alone would only happen rarely. We can estimate the probability using the results object.

In our simulations, only 2.6% of the simulated test statistics were less than or equal to the observed test statistic, as or more extreme relative to the null hypothesis. Such a low probability indicates that observing such a large difference in proportions from chance alone is rare. This probability is known as a \(p\) -value . The \(p\) -value is a conditional probability, the probability of the observed value or more extreme given that the null hypothesis is true.

We could have also found the exact \(p\) -value using the hypergeometric distribution. We have 13 not_promoted positions, so we could have anywhere between 0 and 13 females not promoted. We observed 10 females not promoted. Thus, the exact \(p\) -value from the hypergeometric distribution is the probability of 10 or more females not promoted (as or more extreme than the observed) when we select 13 people from a pool of 24 males and 24 females, and the selection is done without replacement.

Again, we see a low probability, only 2.4%, of observing 10 or more females not promoted, given that the null hypothesis is true.

The observed difference of -29.2% is a rare (low probability) event if there truly is no impact from listing gender in the personnel files. This provides us with two possible interpretations of the study results, in context of our hypotheses:

\(H_0\) : Null hypothesis. Gender has no effect on promotion decision, and we observed a difference that is so large that it would only happen rarely. \(H_A\) : Alternative hypothesis. Gender has an effect on promotion decision, and what we observed was actually due to equally qualified women being discriminated against in promotion decisions, which explains the large difference of -29.2%.

When we conduct formal studies, we reject a skeptical position ( \(H_0\) ) if the data strongly conflict with that position. 82

In our analysis, we determined that there was only a ~ 2% probability of obtaining a test statistic where the difference between female and male promotion proportions was 29.2% or larger assuming gender had no impact. So we conclude the data provide sufficient evidence of gender discrimination against women by the supervisors. In this case, we reject the null hypothesis in favor of the alternative hypothesis.

Statistical inference is the practice of making decisions and conclusions from data in the context of uncertainty. Errors do occur, just like rare events, and the data set at hand might lead us to the wrong conclusion. While a given data set may not always lead us to a correct conclusion, statistical inference gives us tools to control and evaluate how often these errors occur.

Let’s summarize what we did in this case study. We had a research question and some data to test the question. We then performed 4 steps:

• State the null and alternative hypotheses.
• Compute a test statistic.
• Determine the \(p\) -value.
• Draw a conclusion.

We decided to use a randomization test, a simulation, to answer the question. When creating a randomization distribution, we attempted to satisfy 3 guiding principles.

• Be consistent with the null hypothesis. We need to simulate a world in which the null hypothesis is true. If we don’t do this, we won’t be testing our null hypothesis. In our problem, we assumed gender and promotion were independent.
• Use the data in the original sample. The original data should shed light on some aspects of the distribution that are not determined by the null hypothesis. For our problem, we used the difference in promotion rates. The data does not give us the distribution direction, but it gives us an idea that there is a large difference.
• Reflect the way the original data were collected. There were 48 files and 48 supervisors. A total of 35 files were recommended for promotion. We keep this the same in our simulation.

The remainder of this block expands on the ideas of this case study.

16.5 Homework Problems

• Side effects of Avandia . Rosiglitazone is the active ingredient in the controversial type~2 diabetes medicine Avandia and has been linked to an increased risk of serious cardiovascular problems such as stroke, heart failure, and death. A common alternative treatment is pioglitazone, the active ingredient in a diabetes medicine called Actos. In a nationwide retrospective observational study of 227,571 Medicare beneficiaries aged 65 years or older, it was found that 2,593 of the 67,593 patients using rosiglitazone and 5,386 of the 159,978 using pioglitazone had serious cardiovascular problems. These data are summarized in the contingency table below.

\[ \begin{array}{cc|ccc} & & &\textit{Cardiovascular problems}\\ & & \text{Yes} & \text{No} & \textbf{Total} \\ & \hline \text{Rosiglitazone} & 2,593 & 65,000 & 67,593 \\ \textit{Treatment}& \text{Pioglitazone} & 5,386 & 154,592 & 159,978 \\ & \textbf{Total} & 7,979 & 219,592 & 227,571 \\ \end{array} \]

Determine if each of the following statements is true or false. If false, explain why. The reasoning may be wrong even if the statement’s conclusion is correct. In such cases, the statement should be considered false.

Since more patients on pioglitazone had cardiovascular problems (5,386 vs. 2,593), we can conclude that the rate of cardiovascular problems for those on a pioglitazone treatment is higher.

The data suggest that diabetic patients who are taking rosiglitazone are more likely to have cardiovascular problems since the rate of incidence was (2,593 / 67,593 = 0.038) 3.8% for patients on this treatment, while it was only (5,386 / 159,978 = 0.034) 3.4% for patients on pioglitazone.

The fact that the rate of incidence is higher for the rosiglitazone group proves that rosiglitazone causes serious cardiovascular problems.

Based on the information provided so far, we cannot tell if the difference between the rates of incidences is due to a relationship between the two variables or due to chance.

Heart transplants . The Stanford University Heart Transplant Study was conducted to determine whether an experimental heart transplant program increased lifespan. Each patient entering the program was designated an official heart transplant candidate, meaning that he was gravely ill and would most likely benefit from a new heart. Some patients got a transplant and some did not. The variable indicates which group the patients were in; patients in the treatment group got a transplant and those in the control group did not. Another variable called was used to indicate whether or not the patient was alive at the end of the study.

In the study, of the 34 patients in the control group, 4 were alive at the end of the study. Of the 69 patients in the treatment group, 24 were alive. The contingency table below summarizes these results.

\[ \begin{array}{cc|ccc} & & &\textit{Group}\\ & & \text{Control} & \text{Treatment} & \textbf{Total} \\ & \hline \text{Alive} & 4 & 24 & 28 \\ \textit{Outcome}& \text{Dead} & 30 & 45 & 75 \\ & \textbf{Total} & 34 & 69 & 103\\ \end{array} \]

The data is in a file called Stanford_heart_study.csv . Read the data in and answer the following questions.

What proportion of patients in the treatment group and what proportion of patients in the control group died? Note: One approach for investigating whether or not the treatment is effective is to use a randomization technique.

What are the claims being tested? Use the same null and alternative hypothesis notation used in the chapter notes.

The paragraph below describes the set up for such approach, if we were to do it without using statistical software. Fill in the blanks with a number or phrase, whichever is appropriate.

We write alive on _______ cards representing patients who were alive at the end of the study, and dead on _______ cards representing patients who were not. Then, we shuffle these cards and split them into two groups: one group of size _______ representing treatment, and another group of size _______ representing control. We calculate the difference between the proportion of cards in the control and treatment groups (control - treatment), this is just so we have positive observed value, and record this value. We repeat this many times to build a distribution centered at _______. Lastly, we calculate the fraction of simulations where the simulated differences in proportions are _______ or _______. If this fraction of simulations, the empirical \(p\) -value, is low, we conclude that it is unlikely to have observed such an outcome by chance and that the null hypothesis should be rejected in favor of the alternative.

Next we will perform the simulation and use results to decide the effectiveness of the transplant program.

Find observed value of the test statistic, which we decided to use the difference in proportions.

Simulate 1000 values of the test statistic by using shuffle() on the variable group .

Plot distribution of results. Include a vertical line for the observed value. Clean up the plot as if you were presenting to a decision maker.

Find \(p\) -value. Think carefully about what more extreme would mean.

Decide if the treatment is effective.

Solutions Manual

• Free Courses
• Career Guide

Recommended Data Science Courses

Data Science and Machine Learning from MIT

Earn an MIT IDSS certificate in Data Science and Machine Learning. Learn from MIT faculty, with hands-on training, mentorship, and industry projects.

PG in Data Science & Business Analytics from UT Austin

Advance your career with our 12-month Data Science and Business Analytics program from UT Austin. Industry-relevant curriculum with hands-on projects.

Introduction to Hypothesis Testing in R

Testing of hypothesis in r, p-value: an alternative way of hypothesis testing:, t-test: hypothesis testing of population mean when population standard deviation is unknown:, two samples tests: hypothesis testing for the difference between two population means, hypothesis testing for equality of population variances, let’s look at some case studies:, references:, hypothesis testing in r- introduction examples and case study.

– By Dr. Masood H. Siddiqui, Professor & Dean (Research) at Jaipuria Institute of Management, Lucknow

The premise of Data Analytics is based on the philosophy of the “ Data-Driven Decision Making ” that univocally states that decision-making based on data has less probability of error than those based on subjective judgement and gut-feeling. So, we require data to make decisions and to answer the business/functional questions. Data may be collected from each and every unit/person, connected with the problem-situation (totality related to the situation). This is known as Census or Complete Enumeration and the ‘totality’ is known as Population . Obv.iously, this will generally give the most optimum results with maximum correctness but this may not be always possible. Actually, it is rare to have access to information from all the members connected with the situation. So, due to practical considerations, we take up a representative subset from the population, known as Sample . A sample is a representative in the sense that it is expected to exhibit the properties of the population, from where it has been drawn. 

So, we have evidence (data) from the sample and we need to decide for the population on the basis of that data from the sample i.e. inferring about the population on the basis of a sample. This concept is known as Statistical Inference . 

Before going into details, we should be clear about certain terms and concepts that will be useful:

Parameter and Statistic

Parameters are unknown constants that effectively define the population distribution , and in turn, the population , e.g. population mean (µ), population standard deviation (σ), population proportion (P) etc. Statistics are the values characterising the sample i.e. characteristics of the sample. They are actually functions of sample values e. g. sample mean (x̄), sample standard deviation (s), sample proportion (p) etc. 

Sampling Distribution

A large number of samples may be drawn from a population. Each sample may provide a value of sample statistic, so there will be a distribution of sample statistic value from all the possible samples i.e. frequency distribution of sample statistic . This is better known as Sampling distribution of the sample statistic . Alternatively, the sample statistic is a random variable , being a function of sample values (which are random variables themselves). The probability distribution of the sample statistic is known as sampling distribution of sample statistic. Just like any other distribution, sampling distribution may partially be described by its mean and standard deviation . The standard deviation of sampling distribution of a sample statistic is better known as the Standard Error of the sample statistic. 

Standard Error

It is a measure of the extent of variation among different values of statistics from different possible samples. Higher the standard error, higher is the variation among different possible values of statistics. Hence, less will be the confidence that we may place on the value of the statistic for estimation purposes. Hence, the sample statistic having a lower value of standard error is supposed to be better for estimation of the population parameter. 

1(a). A sample of size ‘n’ has been drawn for a normal population N (µ, σ). We are considering sample mean (x̄) as the sample statistic. Then, the sampling distribution of sample statistic x̄ will follow Normal Distribution with mean µ x̄ = µ and standard error σ x̄ = σ/ √ n.

Even if the population is not following the Normal Distribution but for a large sample (n = large), the sampling distribution of x̄ will approach to (approximated by) normal distribution with mean µ x̄ = µ and standard error σ x̄ = σ/ √ n, as per the Central Limit Theorem . 

(b). A sample of size ‘n’ has been drawn for a normal population N (µ, σ), but population standard deviation σ is unknown, so in this case σ will be estimated by sample standard deviation(s). Then, sampling distribution of sample statistic x̄ will follow the student’s t distribution (with degree of freedom = n-1) having mean µ x̄ = µ and standard error σ x̄ = s/ √ n.

2. When we consider proportions for categorical data. Sampling distribution of sample proportion p =x/n (where x = Number of success out of a total of n) will follow Normal Distribution with mean µ p = P and standard error σ p = √( PQ/n), (where Q = 1-P). This is under the condition that n is large such that both np and nq should be minimum 5.

Statistical Inference

Statistical Inference encompasses two different but related problems:

1. Knowing about the population-values on the basis of data from the sample. This is known as the problem of Estimation . This is a common problem in business decision-making because of lack of complete information and uncertainty but by using sample information, the estimate will be based on the concept of data based decision making. Here, the concept of probability is used through sampling distribution to deal with the uncertainty. If sample statistics is used to estimate the population parameter , then in that situation that is known as the Estimator; {like sample mean (x̄) to estimate population mean µ, sample proportion (p) to estimate population proportion (P) etc.}. A particular value of the estimator for a given sample is known as Estimate . For example, if we want to estimate average sales of 1000+ outlets of a retail chain and we have taken a sample of 40 outlets and sample mean ( estimator ) x̄ is 40000. Then the estimate will be 40000.

There are two types of estimation:

• Point Estimation : Single value/number of the estimator is used to estimate unknown population parameters. The example is given above. 
• Confidence Interval/Interval Estimation : Interval Estimate gives two values of sample statistic/estimator, forming an interval or range, within which an unknown population is expected to lie. This interval estimate provides confidence with the interval vis-à-vis the population parameter. For example: 95% confidence interval for population mean sale is (35000, 45000) i.e. we are 95% confident that interval estimate will contain the population parameter.

2. Examining the declaration/perception/claim about the population for its correctness on the basis of sample data. This is known as the problem of Significant Testing or Testing of Hypothesis . This belongs to the Confirmatory Data Analysis , as to confirm or otherwise the hypothesis developed in the earlier Exploratory Data Analysis stage.

One Sample Tests

z-test – Hypothesis Testing of Population Mean when Population Standard Deviation is known:

Hypothesis testing in R starts with a claim or perception of the population. Hypothesis may be defined as a claim/ positive declaration/ conjecture about the population parameter. If hypothesis defines the distribution completely, it is known as Simple Hypothesis, otherwise Composite Hypothesis . 

Hypothesis may be classified as: 

Null Hypothesis (H 0 ): Hypothesis to be tested is known as Null Hypothesis (H 0 ). It is so known because it assumes no relationship or no difference from the hypothesized value of population parameter(s) or to be nullified. 

Alternative Hypothesis (H 1 ): The hypothesis opposite/complementary to the Null Hypothesis .

Note: Here, two points are needed to be considered. First, both the hypotheses are to be constructed only for the population parameters. Second, since H 0 is to be tested so it is H 0 only that may be rejected or failed to be rejected (retained).

Hypothesis Testing: Hypothesis testing a rule or statistical process that may be resulted in either rejecting or failing to reject the null hypothesis (H 0 ).

The Five Steps Process of Hypothesis Testing

Here, we take an example of Testing of Mean:

1. Setting up the Hypothesis:

This step is used to define the problem after considering the business situation and deciding the relevant hypotheses H 0 and H 1 , after mentioning the hypotheses in the business language.

We are considering the random variable X = Quarterly sales of the sales executive working in a big FMCG company. Here, we assume that sales follow normal distribution with mean µ (unknown) and standard deviation σ (known) . The value of the population parameter (population mean) to be tested be µ 0 (Hypothesised Value).

Here the hypothesis may be:

H 0 : µ = µ 0  or µ ≤ µ 0  or µ ≥ µ 0  (here, the first one is Simple Hypothesis , rest two variants are composite hypotheses ) 

H 1 : µ > µ 0 or

H 1 : µ < µ 0 or

H 1 : µ ≠ µ 0 

(Here, all three variants are Composite Hypothesis )

2. Defining Test and Test Statistic:

The test is the statistical rule/process of deciding to ‘reject’ or ‘fail to reject’ (retain) the H0. It consists of dividing the sample space (the totality of all the possible outcomes) into two complementary parts. One part, providing the rejection of H 0 , known as Critical Region . The other part, representing the failing to reject H 0 situation , is known as Acceptance Region .

The logic is, since we have evidence only from the sample, we use sample data to decide about the rejection/retaining of the hypothesised value. Sample, in principle, can never be a perfect replica of the population so we do expect that there will be variation in between population and sample values. So the issue is not the difference but actually the magnitude of difference . Suppose, we want to test the claim that the average quarterly sale of the executive is 75k vs sale is below 75k. Here, the hypothesised value for the population mean is µ 0 =75 i.e.

H 0 : µ = 75

H 1 : µ < 75.

Suppose from a sample, we get a value of sample mean x̄=73. Here, the difference is too small to reject the claim under H 0 since the chances (probability) of happening of such a random sample is quite large so we will retain H 0 . Suppose, in some other situation, we get a sample with a sample mean x̄=33. Here, the difference between the sample mean and hypothesised population mean is too large. So the claim under H 0 may be rejected as the chance of having such a sample for this population is quite low.

So, there must be some dividing value (s) that differentiates between the two decisions: rejection (critical region) and retention (acceptance region), this boundary value is known as the critical value .

Type I and Type II Error:

There are two types of situations (H 0 is true or false) which are complementary to each other and two types of complementary decisions (Reject H 0 or Failing to Reject H 0 ). So we have four types of cases:

So, the two possible errors in hypothesis testing can be:

Type I Error = [Reject H 0 when H 0 is true]

Type II Error = [Fails to reject H 0 when H 0 is false].

Type I Error is also known as False Positive and Type II Error is also known as False Negative in the language of Business Analytics.

Since these two are probabilistic events, so we measure them using probabilities:

α = Probability of committing Type I error = P [Reject H 0 / H 0 is true] 

β = Probability of committing Type II error = P [Fails to reject H 0 / H 0 is false].

For a good testing procedure, both types of errors should be low (minimise α and β) but simultaneous minimisation of both the errors is not possible because they are interconnected. If we minimize one, the other will increase and vice versa. So, one error is fixed and another is tried to be minimised. Normally α is fixed and we try to minimise β. If Type I error is critical, α is fixed at a low value (allowing β to take relatively high value) otherwise at relatively high value (to minimise β to a low value, Type II error being critical).

Example: In Indian Judicial System we have H 0 : Under trial is innocent. Here, Type I Error = An innocent person is sentenced, while Type II Error = A guilty person is set free. Indian (Anglo Saxon) Judicial System considers type I error to be critical so it will have low α for this case.

Power of the test = 1- β = P [Reject H 0 / H 0 is false].

Higher the power of the test, better it is considered and we look for the Most Powerful Test since power of test can be taken as the probability that the test will detect a deviation from H 0 given that the deviation exists.

One Tailed and Two Tailed Tests of Hypothesis:

H 0 : µ ≤ µ 0  

H 1 : µ > µ 0 

When x̄ is significantly above the hypothesized population mean µ 0 then H 0 will be rejected and the test used will be right tailed test (upper tailed test) since the critical region (denoting rejection of H 0 will be in the right tail of the normal curve (representing sampling distribution of sample statistic x̄). (The critical region is shown as a shaded portion in the figure).

H 0 : µ ≥ µ 0

H 1 : µ < µ 0 

In this case, if x̄ is significantly below the hypothesised population mean µ 0 then H 0 will be rejected and the test used will be the left tailed test (lower tailed test) since the critical region (denoting rejection of H 0 ) will be in the left tail of the normal curve (representing sampling distribution of sample statistic x̄). (The critical region is shown as a shaded portion in the figure).

These two tests are also known as One-tailed tests as there will be a critical region in only one tail of the sampling distribution.

H 0 : µ = µ 0

H 1 : µ ≠ µ 0

When x̄ is significantly different (significantly higher or lower than) from the hypothesised population mean µ 0 , then H 0 will be rejected. In this case, the two tailed test will be applicable because there will be two critical regions (denoting rejection of H 0 ) on both the tails of the normal curve (representing sampling distribution of sample statistic x̄). (The critical regions are shown as shaded portions in the figure). 

Hypothesis Testing using Standardized Scale: Here, instead of measuring sample statistic (variable) in the original unit, standardised value is taken (better known as test statistic ). So, the comparison will be between observed value of test statistic (estimated from sample), and critical value of test statistic (obtained from relevant theoretical probability distribution).

Here, since population standard deviation (σ) is known, so the test statistics :

Z=  (x- µx̄ x )/σ x̄ = (x- µ 0 )/(σ/√n)  follows Standard Normal Distribution N (0, 1).

3.Deciding the Criteria for Rejection or otherwise:

As discussed, hypothesis testing means deciding a rule for rejection/retention of H 0 . Here, the critical region decides rejection of H 0 and there will be a value, known as Critical Value , to define the boundary of the critical region/acceptance region. The size (probability/area) of a critical region is taken as α . Here, α may be known as Significance Level , the level at which hypothesis testing is performed. It is equal to type I error , as discussed earlier.

Suppose, α has been decided as 5%, so the critical value of test statistic (Z) will be +1.645 (for right tail test), -1.645 (for left tail test). For the two tails test, the critical value will be -1.96 and +1.96 (as per the Standard Normal Distribution Z table). The value of α may be chosen as per the criticality of type I and type II. Normally, the value of α is taken as 5% in most of the analytical situations (Fisher, 1956). 

4. Taking sample, data collection and estimating the observed value of test statistic:

In this stage, a proper sample of size n is taken and after collecting the data, the values of sample mean (x̄) and the observed value of test statistic Z obs is being estimated, as per the test statistic formula.

5. Taking the Decision to reject or otherwise:

On comparing the observed value of Test statistic with that of the critical value, we may identify whether the observed value lies in the critical region (reject H 0 ) or in the acceptance region (do not reject H 0 ) and decide accordingly.

• Right Tailed Test:          If Z obs > 1.645                   : Reject H 0 at 5% Level of Significance.
• Left Tailed Test:            If Z obs < -1.645                  : Reject H 0 at 5% Level of Significance.
• Two Tailed Test:    If Z obs > 1.96 or If Z obs < -1.96  : Reject H 0 at 5% Level of Significance.

There is an alternative approach for hypothesis testing, this approach is very much used in all the software packages. It is known as probability value/ prob. value/ p-value. It gives the probability of getting a value of statistic this far or farther from the hypothesised value if H0 is true. This denotes how likely is the result that we have observed. It may be further explained as the probability of observing the test statistic if H 0 is true i.e. what are the chances in support of occurrence of H 0 . If p-value is small, it means there are less chances (rare case) in favour of H 0 occuring, as the difference between a sample value and hypothesised value is significantly large so H 0 may be rejected, otherwise it may be retained.

If p-value < α       : Reject H 0

If p-value ≥ α : Fails to Reject H 0

So, it may be mentioned that the level of significance (α) is the maximum threshold for p-value. It should be noted that p-value (two tailed test) = 2* p-value (one tailed test). 

Note: Though the application of z-test requires the ‘Normality Assumption’ for the parent population with known standard deviation/ variance but if sample is large (n>30), the normality assumption for the parent population may be relaxed, provided population standard deviation/variance is known (as per Central Limit Theorem).

As we discussed in the previous case, for testing of population mean, we assume that sample has been drawn from the population following normal distribution mean µ and standard deviation σ. In this case test statistic Z = (x- µ 0 )/(σ/√n)  ~ Standard Normal Distribution N (0, 1). But in the situations where population s.d. σ is not known (it is a very common situation in all the real life business situations), we estimate population s.d. (σ) by sample s.d. (s).

Hence the corresponding test statistic: 

t=  (x- µx̄ x )/σ x̄ = (x- µ 0 )/(s/√n) follows Student’s t distribution with (n-1) degrees of freedom. One degree of freedom has been sacrificed for estimating population s.d. (σ) by sample s.d. (s).

Everything else in the testing process remains the same. 

t-test is not much affected if assumption of normality is violated provided data is slightly asymmetrical (near to symmetry) and data-set does not contain outliers.  

t-distribution:

The Student’s t-distribution, is much similar to the normal distribution. It is a symmetric distribution (bell shaped distribution). In general Student’s t distribution is flatter i.e. having heavier tails. Shape of t distribution changes with degrees of freedom (exact distribution) and becomes approximately close to Normal distribution for large n. 

In many business decision making situations, decision makers are interested in comparison of two populations i.e. interested in examining the difference between two population parameters. Example: comparing sales of rural and urban outlets, comparing sales before the advertisement and after advertisement, comparison of salaries in between male and female employees, comparison of salary before and after joining the data science courses etc.

Independent Samples and Dependent (Paired Samples):

Depending on method of collection data for the two samples, samples may be termed as independent or dependent samples. If two samples are drawn independently without any relation (may be from different units/respondents in the two samples), then it is said that samples are drawn independently . If samples are related or paired or having two observations at different points of time on the same unit/respondent, then the samples are said to be dependent or paired .  This approach (paired samples) enables us to compare two populations after controlling the extraneous effect on them.  

Testing the Difference Between Means: Independent Samples

Two samples z test:.

We have two populations, both following Normal populations as N (µ 1 , σ 1 ) and N (µ 2 , σ 2 ). We want to test the Null Hypothesis:

H 0 : µ 1 – µ 2 = θ or µ 1 – µ 2 ≤ θ or µ 1 – µ 2 ≥ θ 

Alternative hypothesis:

H 1 : µ 1 – µ 2 > θ or

H 0 : µ 1 – µ 2 < θ or

H 1 : µ 1 – µ 2 ≠ θ 

(where θ may take any value as per the situation or θ =0). 

Two samples of size n 1 and n 2 have been taken randomly from the two normal populations respectively and the corresponding sample means are x̄ 1 and x̄ 2 .

Here, we are not interested in individual population parameters (means) but in the difference of population means (µ 1 – µ 2 ). So, the corresponding statistic is = (x̄ 1 – x̄ 2 ).

According, sampling distribution of the statistic (x̄ 1 – x̄ 2 ) will follow Normal distribution with mean µ x̄ = µ 1 – µ 2 and standard error σ x̄ = √ (σ² 1 / n 1 + σ² 2 / n 2 ). So, the corresponding Test Statistics will be: 

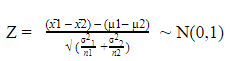
Other things remaining the same as per the One Sample Tests (as explained earlier).

Two Independent Samples t-Test (when Population Standard Deviations are Unknown):

Here, for testing the difference of two population mean, we assume that samples have been drawn from populations following Normal Distributions, but it is a very common situation that population standard deviations (σ 1 and σ 2 ) are unknown. So they are estimated by sample standard deviations (s 1 and s 2 ) from the respective two samples.

Here, two situations are possible:

(a) Population Standard Deviations are unknown but equal:

In this situation (where σ 1 and σ 2 are unknown but assumed to be equal), sampling distribution of the statistic (x̄ 1 – x̄ 2 ) will follow Student’s t distribution with mean µ x̄ = µ 1 – µ 2 and standard error σ x̄ = √ Sp 2 (1/ n 1 + 1/ n 2 ).  Where Sp 2 is the pooled estimate, given by:

Sp 2 = (n 1 -1) S 1 2 +(n 2 -1) S 2 2 /(n 1 +n 2 -2)

So, the corresponding Test Statistics will be: 

t =  {(x̄ 1 – x̄ 2 ) – (µ 1 – µ 2 )}/{√ Sp 2 (1/n 1 +1/n 2 )}

Here, t statistic will follow t distribution with d.f. (n 1 +n 2 -2).

(b) Population Standard Deviations are unknown but unequal:

In this situation (where σ 1 and σ 2 are unknown and unequal).

Then the sampling distribution of the statistic (x̄ 1 – x̄ 2 ) will follow Student’s t distribution with mean µ x̄ = µ 1 – µ 2 and standard error Se =√ (s² 1 / n 1 + s² 2 / n 2 ). 

t =  {(x̄ 1 – x̄ 2 ) – (µ 1 – µ 2 )}/{√ (s2 1 /n 1 +s2 2 /n 2 )}

The test statistic will follow Student’s t distribution with degrees of freedom (rounding down to nearest integers):

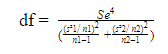
As discussed in the aforementioned two cases, it is important to figure out whether the two population variances are equal or otherwise. For this purpose, F test can be employed as:

H 0 : σ² 1 = σ² 2 and H 1 : σ² 1 ≠ σ² 2

Two samples of sizes n 1 and n 2 have been drawn from two populations respectively. They provide sample standard deviations s 1 and s 2 . The test statistic is F =  s 1 ²/s 2 ²

The test statistic will follow F-distribution with (n 1 -1) df for numerator and (n 2 -1) df for denominator.

Note: There are many other tests that are applied for this purpose.

Paired Sample t-Test (Testing Difference between Means with Dependent Samples):

As discussed earlier, in the situation of Before-After Tests, to examine the impact of any intervention like a training program, health program, any campaign to change status, we have two set of observations (x i and y i ) on the same test unit (respondent or units) before and after the program. Each sample has “n” paired observations. The Samples are said to be dependent or paired.

Here, we consider a random variable: d i = x i – y i . 

Accordingly, the sampling distribution of the sample statistic (sample mean of the differentces d i ’s) will follow Student’s t distribution with mean = θ and standard error = sd/ √ n, where sd is the sample standard deviation of d i ’s.

Hence, the corresponding test statistic: t = (d̅- θ)/sd/√n will follow t distribution with (n-1).

As we have observed, paired t-test is actually one sample test since two samples got converted into one sample of differences. If ‘Two Independent Samples t-Test’ and ‘Paired t-test’ are applied on the same data set then two tests will give much different results because in case of Paired t-Test, standard error will be quite low as compared to Two Independent Samples t-Test. The Paired t-Test is applied essentially on one sample while the earlier one is applied on two samples. The result of the difference in standard error is that t-statistic will take larger value in case of ‘Paired t-Test’ in comparison to the ‘Two Independent Samples t-Test and finally p-values get affected accordingly. 

t-Test in SPSS:

One sample t-test.

• Analyze => Compare Means => One-Sample T-Test to open relevant dialogue box.
• Test variable (variable under consideration) in the Test variable(s) box and hypothesised value µ 0 = 75 (for example) in the Test Value box are to be entered.
• Press Ok to have the output. 

Here, we consider the example of Ventura Sales, and want to examine the perception that average sales in the first quarter is 75 (thousand) vs it is not. So, the Hypotheses:

Null Hypothesis H 0 : µ=75  

Alternative Hypothesis H 1 : µ≠75

One-Sample Statistics

Descriptive table showing the sample size n = 60, sample mean x̄=72.02, sample sd s=9.724.

One-Sample Test

One Sample Test Table shows the result of the t-test. Here, test statistic value (from the sample) is t = -2.376 and the corresponding p-value (2 tailed) = 0.021 <0.05. So, H 0 got rejected and it can be said that the claim of average first quarterly sales being 75 (thousand) does not hold. 

Two Independent Samples t-Test

• Analyze => Compare Means => Independent-Samples T-Test to open the dialogue box.
• Enter the Test variable (variable under consideration) in the Test Variable(s) box and variable categorising the groups in the Grouping Variable box.
• Define the groups by clicking on Define Groups and enter the relevant numeric-codes into the relevant groups in the Define Groups sub-dialogue box. Press Continue to return back to the main dialogue box.

We continue with the example of Ventura Sales, and want to compare the average first quarter sales with respect to Urban Outlets and Rural Outlets (two independent samples/groups). Here, the claim is that urban outlets are giving lower sales as compared to rural outlets. So, the Hypotheses:

H 0 : µ 1 – µ 2 = 0 or µ 1 = µ 2   (Where, µ 1 = Population Mean Sale of Urban Outlets and µ 2 = Population Mean Sale of Rural Outlets)

H 1 : µ 1 < µ 2  

Group Statistics

Descriptive table showing the sample sizes n 1 =37 and n 2 =23, sample means x̄ 1 =67.86 and x̄ 2 =78.70, sample standard deviations s 1 =8.570 and s 2 = 7.600.

The below table is the Independent Sample Test Table, proving all the relevant test statistics and p-values.  Here, both the outputs for Equal Variance (assumed) and Unequal Variance (assumed) are presented.

Independent Samples Test

So, we have to figure out whether we should go for ‘equal variance’ case or for ‘unequal variances’ case. 

Here, Levene’s Test for Equality of Variances has to be applied for this purpose with the hypotheses: H 0 : σ² 1 = σ² 2 and H 1 : σ² 1 ≠ σ² 2 . The p-value (Sig) = 0.460 >0.05, so we can’t reject (so retained) H 0 . Hence, variances can be assumed to be equal. 

So, “Equal Variances assumed” case is to be taken up. Accordingly, the value of t statistic = -4.965 and the p-value (two tailed) = 0.000, so the p-value (one tailed) = 0.000/2 = 0.000 <0.05. Hence, H 0 got rejected and it can be said that urban outlets are giving lower sales in the first quarter. So, the claim stands.

Paired t-Test (Testing Difference between Means with Dependent Samples):

•   Analyze => Compare Means => Paired-Samples T-Test to open the dialogue box.
• Enter the relevant pair of variables (paired samples) in the Paired Variables box.
• After entering the paired samples, press Ok to have the output.

We continue with the example of Ventura Sales, and want to compare the average first quarter sales with the second quarter sales. Some sales promotion interventions were executed with an expectation of increasing sales in the second quarter. So, the Hypotheses:

H 0 : µ 1 = µ 2 (Where, µ 1 = Population Mean Sale of Quarter-I and µ 2 = Population Mean Sale of Quarter-II)

H 1 : µ 1 < µ 2 (representing the increase of sales i.e. implying the success of sales interventions)

Paired Samples Statistics

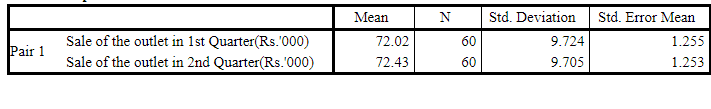
Descriptive table showing the sample size n=60, sample means x̄ 1 =72.02 and x̄ 2 =72.43.

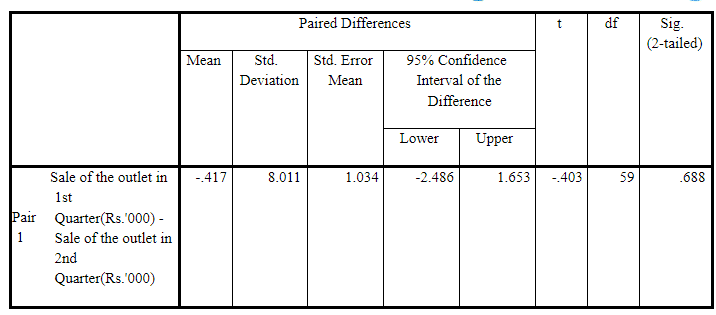
As per the following output table (Paired Samples Test), sample mean of differences d̅ = -0.417 with standard deviation of differences sd = 8.011 and value of t statistic = -0.403. Accordingly, the p-value (two tailed) = 0.688, so the p-value (one tailed) = 0.688/2 = 0.344 > 0.05. So, there have not been sufficient reasons to Reject H 0 i.e. H 0 should be retained. So, the effectiveness (success) of the sales promotion interventions is doubtful i.e. it didn’t result in significant increase in sales, provided all other extraneous factors remain the same.

Paired Samples Test   

t-Test Application One Sample

Experience Marketing Services reported that the typical American spends a mean of 144 minutes (2.4 hours) per day accessing the Internet via a mobile device. (Source: The 2014 Digital Marketer, available at ex.pn/1kXJifX.) To test the validity of this statement, you select a sample of 30 friends and family. The result for the time spent per day accessing the Internet via a mobile device (in minutes) are stored in Internet_Mobile_Time.csv file.

Is there evidence that the populations mean time spent per day accessing the Internet via a mobile device is different from 144 minutes? Use the p-value approach and a level of significance of 0.05

What assumption about the population distribution is needed to conduct the test in A?

Solution In R

[1] 1.224674

[1] 0.2305533

[1] “Accepted”

Independent t-test two sample

A hotel manager looks to enhance the initial impressions that hotel guests have when they check-in. Contributing to initial impressions is the time it takes to deliver a guest’s luggage to the room after check-in. A random sample of 20 deliveries on a particular day was selected each from Wing A and Wing B of the hotel. The data collated is given in Luggage.csv file. Analyze the data and determine whether there is a difference in the mean delivery times in the two wings of the hotel. (use alpha = 0.05).

    Two Sample t-test data:  WingA and WingB t = 5.1615, df = 38, p-value = 4.004e-06 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 1.531895   Inf sample estimates: mean of x mean of y  10.3975 8.1225 > t.test(WingA,WingB)    Welch Two Sample t-test

t = 5.1615, df = 37.957, p-value = 8.031e-06 alternative hypothesis: true difference in means is not equal to 0 95 per cent confidence interval: 1.38269 3.16731 sample estimates: mean of x mean of y  10.3975 8.1225

Case Study- Titan Insurance Company

The Titan Insurance Company has just installed a new incentive payment scheme for its lift policy salesforce. It wants to have an early view of the success or failure of the new scheme. Indications are that the sales force is selling more policies, but sales always vary in an unpredictable pattern from month to month and it is not clear that the scheme has made a significant difference.

Life Insurance companies typically measure the monthly output of a salesperson as the total sum assured for the policies sold by that person during the month. For example, suppose salesperson X has, in the month, sold seven policies for which the sums assured are £1000, £2500, £3000, £5000, £10000, £35000. X’s output for the month is the total of these sums assured, £61,500.

Titan’s new scheme is that the sales force receives low regular salaries but are paid large bonuses related to their output (i.e. to the total sum assured of policies sold by them). The scheme is expensive for the company, but they are looking for sales increases which more than compensate. The agreement with the sales force is that if the scheme does not at least break even for the company, it will be abandoned after six months.

The scheme has now been in operation for four months. It has settled down after fluctuations in the first two months due to the changeover.

To test the effectiveness of the scheme, Titan has taken a random sample of 30 salespeople measured their output in the penultimate month before changeover and then measured it in the fourth month after the changeover (they have deliberately chosen months not too close to the changeover). Ta ble 1 shows t he outputs of the salespeople in Table 1

Data preparation

Since the given data are in 000, it will be better to convert them in thousands. Problem 1 Describe the five per cent significance test you would apply to these data to determine whether the new scheme has significantly raised outputs? What conclusion does the test lead to? Solution: It is asked that whether the new scheme has significantly raised the output, it is an example of the one-tailed t-test. Note: Two-tailed test could have been used if it was asked “new scheme has significantly changed the output” Mean of amount assured before the introduction of scheme = 68450 Mean of amount assured after the introduction of scheme = 72000 Difference in mean = 72000 – 68450 = 3550 Let, μ1 = Average sums assured by salesperson BEFORE changeover. μ2 = Average sums assured by salesperson AFTER changeover. H0: μ1 = μ2  ; μ2 – μ1 = 0 HA: μ1 < μ2   ; μ2 – μ1 > 0 ; true difference of means is greater than zero. Since population standard deviation is unknown, paired sample t-test will be used.

Since p-value (=0.06529) is higher than 0.05, we accept (fail to reject) NULL hypothesis. The new scheme has NOT significantly raised outputs .

Problem 2 Suppose it has been calculated that for Titan to break even, the average output must increase by £5000. If this figure is an alternative hypothesis, what is: (a)  The probability of a type 1 error? (b)  What is the p-value of the hypothesis test if we test for a difference of $5000? (c)   Power of the test: Solution: 2.a.  The probability of a type 1 error? Solution: Probability of Type I error = significant level = 0.05 or 5% 2.b.  What is the p-value of the hypothesis test if we test for a difference of $5000? Solution: Let  μ2 = Average sums assured by salesperson AFTER changeover. μ1 = Average sums assured by salesperson BEFORE changeover. μd = μ2 – μ1   H0: μd ≤ 5000 HA: μd > 5000 This is a right tail test.

P-value = 0.6499 2.c. Power of the test. Solution: Let  μ2 = Average sums assured by salesperson AFTER changeover. μ1 = Average sums assured by salesperson BEFORE changeover. μd = μ2 – μ1   H0: μd = 4000 HA: μd > 0

H0 will be rejected if test statistics > t_critical. With α = 0.05 and df = 29, critical value for t statistic (or t_critical ) will be   1.699127. Hence, H0 will be rejected for test statistics ≥  1.699127. Hence, H0 will be rejected if for  𝑥̅ ≥ 4368.176

Graphically,

      Probability (type II error) is P(Do not reject H0 | H0 is false)       Our NULL hypothesis is TRUE at μd = 0 so that  H0: μd = 0 ; HA: μd > 0       Probability of type II error at μd = 5000

= P (Do not reject H0 | H0 is false) = P (Do not reject H0 | μd = 5000)  = P (𝑥̅ < 4368.176 | μd = 5000) = P (t <  | μd = 5000) = P (t < -0.245766) = 0.4037973

R Code: Now,  β=0.5934752, Power of test = 1- β = 1- 0.5934752 = 0.4065248

• While performing Hypothesis-Testing, Hypotheses can’t be proved or disproved since we have evidence from sample (s) only. At most, Hypotheses may be rejected or retained.
• Use of the term “accept H 0 ” in place of “do not reject” should be avoided even if the test statistic falls in the Acceptance Region or p-value ≥ α. This simply means that the sample does not provide sufficient statistical evidence to reject the H 0 . Since we have tried to nullify (reject) H 0 but we haven’t found sufficient support to do so, we may retain it but it won’t be accepted.
• Confidence Interval (Interval Estimation) can also be used for testing of hypotheses. If the hypothesis parameter falls within the confidence interval, we do not reject H 0 . Otherwise, if the hypothesised parameter falls outside the confidence interval i.e. confidence interval does not contain the hypothesized parameter, we reject H 0 .
• Downey, A. B. (2014). Think Stat: Exploratory Data Analysis , 2 nd Edition, Sebastopol, CA: O’Reilly Media Inc
• Fisher, R. A. (1956). Statistical Methods and Scientific Inference , New York: Hafner Publishing Company.
• Hogg, R. V.; McKean, J. W. & Craig, A. T. (2013). Introduction to Mathematical Statistics , 7 th Edition, New Delhi: Pearson India.
• IBM SPSS Statistics. (2020). IBM Corporation. 
• Levin, R. I.; Rubin, D. S; Siddiqui, M. H. & Rastogi, S. (2017). Statistics for Management , 8 th Edition, New Delhi: Pearson India. 

If you want to get a detailed understanding of Hypothesis testing, you can take up this hypothesis testing in machine learning course. This course will also provide you with a certificate at the end of the course.

If you want to learn more about R programming and other concepts of Business Analytics or Data Science, sign up for Great Learning ’s PG program in Data Science and Business Analytics.

→ Explore this Curated Program for You ←

Understanding the Exploratory Data Analysis (EDA) in Python

Inferential Statistics – An Overview | Introduction to Inferential Statistics

An Introduction to Descriptive Statistics | Definition of Descriptive Statistics

Industries most and least impacted by COVID-19: A Quick Look

See How Automotive Industry Uses Analytics to Solve Business Problems With Case Studies

5 Examples of HR Professionals Using Analytics For Better Productivity

• Search Menu

Sign in through your institution

• Browse content in Arts and Humanities
• Browse content in Archaeology
• Historical Archaeology
• Browse content in Architecture
• History of Architecture
• Browse content in Art
• History of Art
• Browse content in Classical Studies
• Classical Literature
• Religion in the Ancient World
• Browse content in History
• Colonialism and Imperialism
• History by Period
• Intellectual History
• Military History
• Political History
• Regional and National History
• Social and Cultural History
• Theory, Methods, and Historiography
• Browse content in Literature
• Literary Studies (Romanticism)
• Literary Studies (European)
• Literary Studies - World
• Literary Studies (19th Century)
• Literary Studies (African American Literature)
• Literary Studies (Early and Medieval)
• Literary Studies (Poetry and Poets)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Media Studies
• Browse content in Music
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Philosophy of Language
• Philosophy of Science
• Philosophy of Religion
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• History of Religion
• Judaism and Jewish Studies
• Religious Studies
• Society and Culture
• Browse content in Law
• Company and Commercial Law
• Comparative Law
• Constitutional and Administrative Law
• Criminal Law
• History of Law
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Molecular and Cell Biology
• Zoology and Animal Sciences
• Browse content in Computer Science
• Programming Languages
• Environmental Science
• History of Science and Technology
• Browse content in Mathematics
• Applied Mathematics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Browse content in Physics
• Astronomy and Astrophysics
• Biological and Medical Physics
• Computational Physics
• Condensed Matter Physics
• History of Physics
• Mathematical and Statistical Physics
• Browse content in Psychology
• Cognitive Neuroscience
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Regional Anthropology
• Social and Cultural Anthropology
• Browse content in Business and Management
• Business History
• Industry Studies
• International Business
• Knowledge Management
• Public and Nonprofit Management
• Criminology and Criminal Justice
• Browse content in Economics
• Asian Economics
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic History
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• History of Economic Thought
• International Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Browse content in Education
• Higher and Further Education
• Browse content in Politics
• Asian Politics
• Comparative Politics
• Conflict Politics
• Environmental Politics
• International Relations
• Political Economy
• Political Sociology
• Political Theory
• Public Policy
• Security Studies
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• Asian Studies
• Middle Eastern Studies
• Native American Studies
• Browse content in Social Work
• Social Work and Crime and Justice
• Browse content in Sociology
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Health, Illness, and Medicine
• Migration Studies
• Occupations, Professions, and Work
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Urban and Rural Studies
• Reviews and Awards
• Journals on Oxford Academic
• Books on Oxford Academic

• < Previous chapter
• Next chapter >

14 Case Selection and Hypothesis Testing

• Published: September 2012
• Cite Icon Cite
• Permissions Icon Permissions

This chapter discusses quantitative and qualitative practices of case-study selection when the goal of the analysis is to evaluate causal hypotheses. More specifically, it considers how the different causal models used in the qualitative and quantitative research cultures shape the kind of cases that provide the most leverage for hypothesis testing. The chapter examines whether one should select cases based on their value on the dependent variable. It also evaluates the kinds of cases that provide the most leverage for causal inference when conducting case-study research. It shows that differences in research goals between quantitative and qualitative scholars yield distinct ideas about best strategies of case selection. Qualitative research places emphasis on explaining particular cases; quantitative research does not.

Signed in as

Institutional accounts.

• Google Scholar Indexing
• GoogleCrawler [DO NOT DELETE]

Personal account

• Sign in with email/username & password
• Get email alerts
• Save searches
• Purchase content
• Activate your purchase/trial code
• Add your ORCID iD

Institutional access

Sign in with a library card.

• Sign in with username/password
• Recommend to your librarian
• Institutional account management
• Get help with access

Access to content on Oxford Academic is often provided through institutional subscriptions and purchases. If you are a member of an institution with an active account, you may be able to access content in one of the following ways:

IP based access

Typically, access is provided across an institutional network to a range of IP addresses. This authentication occurs automatically, and it is not possible to sign out of an IP authenticated account.

Choose this option to get remote access when outside your institution. Shibboleth/Open Athens technology is used to provide single sign-on between your institution’s website and Oxford Academic.

• Click Sign in through your institution.
• Select your institution from the list provided, which will take you to your institution's website to sign in.
• When on the institution site, please use the credentials provided by your institution. Do not use an Oxford Academic personal account.
• Following successful sign in, you will be returned to Oxford Academic.

If your institution is not listed or you cannot sign in to your institution’s website, please contact your librarian or administrator.

Enter your library card number to sign in. If you cannot sign in, please contact your librarian.

Society Members

Society member access to a journal is achieved in one of the following ways:

Sign in through society site

Many societies offer single sign-on between the society website and Oxford Academic. If you see ‘Sign in through society site’ in the sign in pane within a journal:

• Click Sign in through society site.
• When on the society site, please use the credentials provided by that society. Do not use an Oxford Academic personal account.

If you do not have a society account or have forgotten your username or password, please contact your society.

Sign in using a personal account

Some societies use Oxford Academic personal accounts to provide access to their members. See below.

A personal account can be used to get email alerts, save searches, purchase content, and activate subscriptions.

Some societies use Oxford Academic personal accounts to provide access to their members.

Viewing your signed in accounts

Click the account icon in the top right to:

• View your signed in personal account and access account management features.
• View the institutional accounts that are providing access.

Signed in but can't access content

Oxford Academic is home to a wide variety of products. The institutional subscription may not cover the content that you are trying to access. If you believe you should have access to that content, please contact your librarian.

For librarians and administrators, your personal account also provides access to institutional account management. Here you will find options to view and activate subscriptions, manage institutional settings and access options, access usage statistics, and more.

Our books are available by subscription or purchase to libraries and institutions.

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Rights and permissions
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

12   Case Study: Hypothesis Testing

For this chapter, we use the NHANESsample dataset seen in Chapter  4 . The sample contains lead, blood pressure, BMI, smoking status, alcohol use, and demographic variables from NHANES 1999-2018. Variable selection and feature engineering were conducted to replicate the preprocessing conducted by Huang ( 2022 ) . We further replicate the regression analysis by Huang ( 2022 ) in Chapter  13 . Use the help operator ?NHANESsample to read the variable descriptions. Note that we ignore survey weights for this analysis.

Our analysis focuses on using hypothesis testing to look at the association between hypertension and blood lead levels by sex. We first select some demographic and clinical variables that we believe may be relevant, including age, sex, race, body mass index, and smoking status. We do a complete case analysis and drop any observations with missing data.

We begin with a summary table stratified by hypertension status. As expected, we see statistically significant differences between the two groups across all included variables. We also observe higher blood lead levels and a higher proportion of male participants for those with hypertension.

We also plot the distribution of blood lead levels (on a log scale) by sex and hypertension status. We can visually see that male observations tend to have higher blood lead levels and that having hypertension is associated with higher blood lead levels.

In Chapter  10 , we explored that log blood lead levels could be approximated by a normal distribution. To test our hypothesis that there is a difference in mean log blood lead level between those with and without hypertension, we use a two-sample unpaired t-test. This shows a statistically significant difference between the two groups at the 0.05 level.

Finally, we repeat this test for a stratified analysis and present the results in a concise table. For both groups, we find a statistically significant difference at the 0.05 level.

In Chapter  13 , we use linear regression to further explore the association between blood lead level and hypertension adjusting for other potential confounders.