Why Variances Add—And Why It Matters
The pythagorean theorem of statistics.
Quick. What’s the most important theorem in statistics? That’s easy. It’s the central limit theorem (CLT), hands down. Okay, how about the second most important theorem? I say it’s the fact that for the sum or difference of independent random variables, variances add:
For independent random variables X and Y ,
I like to refer to this statement as the Pythagorean theorem of statistics for several reasons:
- Just as the Pythagorean theorem applies only to right triangles, this relationship applies only to independent random variables.
- The name helps students remember both the relationship and the restriction.
As you may suspect, this analogy is more than a mere coincidence. There’s a nice geometric model that represents random variables as vectors whose lengths correspond to their standard deviations. When the variables are independent, the vectors are orthogonal. Then the standard deviation of the sum or difference of the variables is the hypotenuse of a right triangle.
You probably won’t discuss orthogonal vectors with your AP Statistics students, but that’s no excuse for not giving the Pythagorean theorem the emphasis it deserves. When your students understand and learn to use this theorem, many doors open. They gain important insights in dealing with binomial probabilities, inference, and even the CLT itself — and they gain an important problem-solving skill sure to pay off on the AP Exam.

Some Questions
Let’s start by taking a look at the theorem itself. Three questions come to mind:
- Why do we add the variances ?
- Why do we add even when working with the difference of the random variables?
- Why do the variables have to be independent ?
I’ll answer these questions on two levels. On one level is the proof, just to make you feel better. Although some teachers may decide to show this proof to their classes, most won’t inflict it on AP Statistics students. Instead, a plausibility argument should suffice. By that I mean a series of justifications that stop short of being formal proofs yet give students clear examples that make the theorem something believable and vital, not simply a meaningless rule to memorize.
Proving the Theorem: The Math
First, then, let’s have a look at a formal proof. It’s a rule of mathematics that no proof should be taken seriously unless there’s a lemma, so here’s ours. The proof uses the fact that, because expected values are basically summations, they are additive:
And now, the Pythagorean theorem of statistics:
Consider that middle term: E(xy) - µ x µ y .
E(xy) is the sum of all terms of the form x i y j ·P ( x i ∩ y j ) . The product µ x µ y is the sum of all terms of the form x i P ( x i ) · y j P ( y j ) . If X and Y are independent , each term in the first sum is equal to the corresponding term in the second sum; hence that middle term is 0. Thus:
Note that this proof answers all three questions we posed. It’s the variances that add. Variances add for the sum and for the difference of the random variables because the plus-or-minus terms dropped out along the way. And independence was why part of the expression vanished, leaving us with the sum of the variances.
Teaching the Theorem
Although that proof may make you feel better about the theorem (or not), it’s not likely to warm the hearts of most of your students. Let’s have a look at some arguments you can make in class that show your students the theorem makes sense.
Question 2: Why add even for the difference of the variables? We buy some cereal. The box says “16 ounces.” We know that’s not precisely the weight of the cereal in the box, just close. After all, one corn flake more or less would change the weight ever so slightly. Weights of such boxes of cereal vary somewhat, and our uncertainty about the exact weight is expressed by the variance (or standard deviation) of those weights.
Next we get out a bowl that holds 3 ounces of cereal and pour it full. Our pouring skill is not very precise, so the bowl now contains about 3 ounces with some variability (uncertainty).
How much cereal is left in the box? Well, we assume about 13 ounces. But notice that we’re less certain about this remaining weight than we were about the weight before we poured out the bowlful. The variability of the weight in the box has increased even though we subtracted cereal.
Moral: Every time something happens at random, whether it adds to the pile or subtracts from it, uncertainty (read “variance”) increases.
Question 2 (follow-up): Okay, but is the effect exactly the same when we subtract as when we add? Suppose we have some grapefruit weighing between 16 and 24 ounces and some oranges weighing between 9 and 13 ounces. We pick one of each at random.
- Consider the total possible weight of the two fruits. The maximum total is 24 + 13 = 37 ounces, and the minimum is 16 + 9 = 25 ounces – a range of 12 ounces.
- Now consider the possible weight difference. The maximum difference is 24 - 9 = 15 ounces, and the minimum is 16 - 13 = 3 ounces—again a range of 12 ounces. So whether we’re adding or subtracting the random variables, the resulting range (one measure of variability) is exactly the same. That’s a plausibility argument that the standard deviations of the sum, and the difference should be the same, too.
Question 3: Why do the variables have to be independent? Consider a survey in which we ask people two questions:
- During the last 24 hours, how many hours were you asleep?
- And how many hours were you awake?
There will be some mean number of sleeping hours for the group, with some standard deviation. There will also be a mean and standard deviation of waking hours. But now let’s sum the two answers for each person. What’s the standard deviation of this sum? It’s 0, because that sum is 24 hours for everyone—a constant. Clearly, variances did not add here.
Why not? These data are paired, not independent, as required by the theorem. Just as we can’t apply the Pythagorean theorem without first being sure we are dealing with a right triangle, we can’t add variances until we’re sure the random variables are independent. (This is yet another place where students must remember to check a condition before proceeding.)
Why Does It Matter?
Many teachers wonder if teaching this theorem is worth the struggle. I say getting students to understand this key concept (1) is not that difficult and (2) pays off throughout the course, on the AP Exam, and in future work our students do in statistics. In fact, it comes up so often that the statement “For sums or differences of independent random variables, variances add” is a mantra in my classroom. Let’s take a tour of some of the places the Pythagorean theorem of statistics holds the key to understanding.
Working with Sums
Remember Matt and Dave’s Video Venture, a multiple-choice question from the 1997 AP Exam? At Matt and Dave’s, every Thursday was Roll-the-Dice Day, allowing patrons to rent a second video at a discount determined by the digits rolled on two dice. Students were told that these second movies would cost an average of $0.47, with a standard deviation is $0.15. Then they were asked:
If a customer rolls the dice and rents a second movie every Thursday for 30 consecutive weeks, what is the approximate probability that the total amount paid for these second movies will exceed $15.00?
One route to the solution adds variances.
First we note that the total amount paid is the sum of 30 daily values of a random variable.
We find the expected total.
Because rolls of the dice are independent, we can apply the Pythagorean theorem to find the variance of the total, and that gives us the standard deviation.
The CLT tells us that sums (essentially the same thing as means) of independent random variables approach a normal model as n increases. With n = 30 here, we can safely estimate the probability that T > 15.00 by working with the model N(14.10, 0.822).
Working with Differences
On the 2000 AP Exam, the investigative task asked students to consider heights of men and women. They were given that the heights of each sex are described by a normal model. Means were given as 70 inches for men and 65 inches for women, with standard deviations of 3 inches and 2.5 inches, respectively. Among the questions asked was:
Suppose a married man and a married woman are each selected at random. What is the probability the woman will be taller than the man?
Again, we can solve the problem by adding variances:
First, define the random variables.
M = Height of the chosen man, W = Height of the woman.
We’re interested in the difference of their heights.
Let D = Difference in their heights: D = M - W .
Because the people were selected at random, the heights are independent, so we can find the standard deviation of the difference using the Pythagorean theorem.
The difference of two normal random variables is also normal, so we can now find the probability that the woman is taller using the z-score for a difference of 0.
Standard Deviation for the Binomial
How many 4s do we expect when we roll 600 dice? 100 seems pretty obvious, and students rarely question the fact that for a binomial model µ = np . However, the standard deviation is not so obvious. Let’s derive that formula.
We start by looking at a probability model for a single Bernoulli trial.
Let X = the number of successes.
We find the mean of this random variable.
And then the variance.
Now we count the number of successes in n independent trials.
The mean is no surprise.
And the standard deviation? Just add variances.
The Central Limit Theorem
By using the second most important theorem in statistics, we can derive part of the most important theorem. The central limit theorem (CLT) tells us something quite surprising and beautiful: When we sample from any population, regardless of shape, the behavior of sample means (or sums) can be described by a normal model that increases in accuracy as the sample size increases. The result is not just stunning, it’s also quite fortunate because most of the rest of what we teach in AP Statistics would not exist were it not true.
The full proof of the CLT is well beyond the scope of this article. What’s within our grasp is the theorem’s quantification of the variability in these sample means, and the key is (drum roll!) adding variances.
The mean is basically the sum of n independent random variables, so:
Inference for the Difference of Proportions
The Pythagorean theorem also lets students make sense of those otherwise scary-looking formulas for inferences involving two samples. Indeed, I’ve found that students can come up with the formulas for themselves. Here’s how that plays out in my classroom.
To set the stage for this discussion, we’ve just started inference. We first developed the concept of confidence intervals by looking at a confidence interval for a proportion. We then discussed hypothesis tests for a proportion, and we’ve spent a few days practicing the procedures. By now students understand the ideas and can write up both a confidence interval and a hypothesis test, but only for one proportion. When class starts, I propose the following scenario:
Will a group counseling program help people who are using “the patch” actually manage to quit smoking? The idea is to have people attend a weekly group discussion session with a counselor to create a support group. If such a plan actually proved to be more effective than just wearing the patch, we’d seek funding from local health agencies. Describe an appropriate experiment.
We begin by drawing a flowchart for the experiment – a good review lesson. Start with a cohort of volunteer smokers trying to quit. Randomly divide them into two groups. Both groups get the patch. One group also attends these support/counseling sessions. Wait six months. Then compare the success rates in the two groups.
Earlier in the course, this is where the discussion ended, but now we are ready to finish the job and “compare the success rates”:
After six months, 46 of the 143 people who’d worn the patch and participated in the counseling groups successfully quit smoking. Among those who received the patch but no counseling, 30 of 151 quit smoking. Do these results provide evidence that the counseling program is effective?
Students recognize that we need to test a hypothesis, and they point out that this is a different situation because there are two groups. I bet them they can figure out how to do it, and I start writing their suggestions on the board. They propose a hypothesis that the success rates are the same:
I agree, and then I add that we may also write this hypothesis as a statement of no difference:
They dictate the randomization, success/failure, and 10 percent conditions that allow the use of a normal model. They compute the sample proportions and find the observed difference,
Here’s where it gets interesting. They need to find the probability of observing a difference in proportions at least as large as 0.123, when they were expecting a difference of zero.
Good idea, but can we add the variances? Only if the groups are independent. Why are they independent? Randomization! We return to the list of conditions and add one more: the independent group’s condition. At this point, rather than memorizing a list of conditions, everyone clearly realizes why this condition must be met.
Next we look at what happens when we add the variances:
Voila! The students have derived the formula for the standard deviation of the difference of sample proportions; thus it makes sense to them. We still need to talk about issues like using the sample proportions as estimates and pooling, but the basic formula is at hand and understood.
Inference for the Difference of Means
There’s no need to give you a long-winded example that’s analogous to the situation for proportions. It’s enough to see that the standard deviation for the difference of sample means is also based on adding variances. And it’s clear that students can derive it on their own the first time you test a hypothesis about the difference of means of independent groups:
Two-Sample t-Procedures, or Matched Pairs – It Matters!
Without advance fanfare, I propose to the class that we construct a confidence interval to see how many extra miles per gallon we might get if we use premium rather than regular gasoline. I give the students data from an experiment that tried both types of fuel in several cars (a situation involving matched pairs, but I don’t point that out). When we start constructing the confidence interval, invariably someone questions the assumption that two measurements made for the same car are independent. I insist students explain why that matters. The insight that lack of independence prevents adding variances, which in turn renders the formula for a two-sample t-interval incorrect, makes it forever clear to students that they must think carefully about the design under which their data were collected before plunging into the analysis. There’s never a “choice” whether to use a paired differences procedure or a two-sample t-method.
Create One Confidence Interval, or Two?
| Diet S | Diet N | |
|---|---|---|
| n | 36 | 36 |
| Mean | 55 lbs. | 53 lbs. |
| SD | 3 lbs. | 4 lbs. |
Suppose we wonder if a food supplement can increase weight gain in feeder pigs. An experiment randomly assigns some pigs to one of two diets, identical except for the inclusion of the supplement in the feed for Group S but not for Group N. After a few weeks, we weigh the pigs; summaries of the weight gains appear in the table. Is there evidence that the supplement was effective? A reasonable way to try to answer this question is by using confidence intervals, but which approach is correct?
Plan A: Compare confidence intervals for each group. The separate intervals indicate we can be 95 percent confident that pigs fed this dietary supplement for this period of time would gain an average of between 53.90 and 56.01 pounds, while the average gain for those not fed the supplement would be between 51.65 and 54.35 pounds.
Note that these intervals overlap. It appears to be possible that the two diets might result in the same mean weight gain. Because of this, we lack evidence that the supplement is effective.
Plan B: Construct one confidence interval for the difference in mean weight gain. We can be 95 percent confident that pigs fed the food supplement would gain an average of between 0.34 and 3.66 pounds more than those that were not fed this supplement. Because 0 is not in this confidence interval, we have strong evidence that this food supplement can make feeder pigs gain more weight.
The conclusions are contradictory, but it may not be immediately obvious which is correct. Students often see nothing wrong with Plan A. Such a conclusion would be inaccurate. Whether the two intervals overlap depends on whether the two means are farther apart than the sum of the margins of error. The mistake rests in the fact that we shouldn’t add the margins of error. Why not? A confidence interval’s margin of error is based on a standard deviation (well, standard error to be more exact). But standard deviations don’t add; variances do. Plan B’s confidence interval for the difference bases its margin of error on the standard error for the difference of two sample means, calculated by adding the two variances. That’s the correct approach — one confidence interval, not two.
Future Encounters
Even if you’ve sometimes been stuck in the discussion this far, you should at the very least be convinced that adding variances plays a key role in much of the statistics we teach in the AP course. As our students expand their knowledge of statistics by taking more courses beyond AP Statistics, they encounter the Pythagorean theorem again and again. To cite a few places on the horizon:
- Prediction intervals: When we use a regression line to make a prediction, we should include a margin of error around our estimate. That uncertainty involves three independent sources of error: (1) the line may be misplaced vertically because our sample mean only approximates the true mean of the response variable, (2) our sample data only gives us an estimate of the true slope, and (3) individuals vary above and below the line.
- Multiple regression: When we use several independent factors to arrive at an estimate for the response variable, we assess the strength of the model by looking at the total amount of variability it explains. We’re further able to attribute some of that variability to each of the explanatory variables.
- ANOVA: As the name “analysis of variance” suggests, we compare the effects of treatments on multiple groups or assess the effects of several treatments in a multifactor design by comparing the variability seen within groups to the total variability across groups. Here again, the idea of adding variances lies at the heart of the statistics.
Let’s summarize: Variances add. And yes, it matters!
Authored by
Dave Bock Cornell University Ithaca, New York

AP® Statistics
Standard deviation: ap® statistics crash course review.
- The Albert Team
- Last Updated On: March 1, 2022

Standard deviation is used to test variability in statistics by calculating the average distance from the mean of all the values in a data set. Another way to think of it is to ask, “How much do the values in this data set deviate from the mean value?”
The nuts and bolts of the equation are fairly simple—it just has a lot of different components to consider. This crash course will take you through how to calculate and interpret standard deviation. Then we’ll look at an example from the AP® Statistics test.
First Step: Calculating the Mean of a Data Set
In our example, the Smith family has five children. Let’s say we want to find the standard deviation from the mean age of the siblings. Our data set is the five children’s ages:
To find the standard deviation from the mean, we first need to know what our mean, or average, is. To calculate the mean, add each number in the data set:
Then divide your result by the number of values in your data set, or N. We have five values (for five Smith kids), so our N = 5.
9.2, then, is our mean , or µ. The formula for finding the mean of a data set can also be expressed as:
Where \sum_a^b x is the sum of all the values in the data set; N is the number of values in the population, and n is the number of values in the data sample.
Notice that the mean symbol changes when referring to a sample mean versus the population mean. If you are taking the mean of a sample rather than the whole data set, you will want to use the x-bar symbol for mean rather than the µ. Since we are calculating the mean age of all the Smith children, we will use the µ.
You may also see the x in this equation written as . The superscript i simply means individual, telling you to consider each individual x value. Meanwhile, the sigma symbol, ∑, means you have to take the sum of something. So the formula tells you that the mean is equal to the sum of all the x values divided by N.
This may seem pretty basic, but understanding the code of this formula will make understanding the standard deviation formula that much easier.
Next: Calculating the Standard Deviation
The standard deviation is the average distance from the mean. Our µ = 9.2 for the values {3, 7, 8, 12, 16}. Therefore, we need to find the distance of each of those values from the mean, and then calculate the average distance.
The formula is one you’ll want to learn by heart, even though it’s included on the AP® Stats formula sheet. Make sure you include this one on your AP® Statistics study guide.
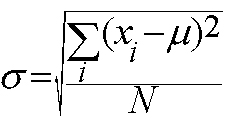
Image Source: Pittsburg State University
This formula represents the standard deviation from the µ. The i superscript is something you may or may not see written out in this equation; it just depends on how clear the writer wants to be. The superscript simply means to take the sum of each individual point in the data set.
Since we’re working with the whole population of Smith children, this is the formula we’ll cover first. Later, we’ll cover the formula for a sample mean. Let’s set up the equation for our data set and go through it step by step:
Our standard deviation is 4.45. That means that each Smith child is an average distance of 4.45 years away from the mean age of all the Smith children.
That’s the basic formula for standard deviation. If you need to find the standard deviation of a sample mean, refer to this formula:
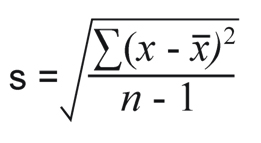
Image Source: Mathematical Musings
The main difference here, apart from the use of the s for sample standard deviation and the x-bar symbol for sample mean, is the n – 1. A lower-case n refers to the sample population while a capital N refers to the total population and n – 1 adjusts for the difference between the sample and the whole.
Interpreting the Standard Deviation
A high standard deviation generally means that the data points are widely scattered from the average while a low standard deviation means that the data points are closer to the mean. This allows you to compare results within a population group. It also allows you to compare standard deviation in results between different population groups. This is particularly useful if you are attempting to reproduce your results in a scientific study.
Say, for instance, that you are testing response times of participants in a driving simulation. The control group is well rested while the 3 experimental groups have had 6, 4, and 2 hours of sleep respectively. The standard deviation in their response times would give valuable insight into how erratic drivers become when sleep-deprived.
Standard deviation can also be expressed graphically:
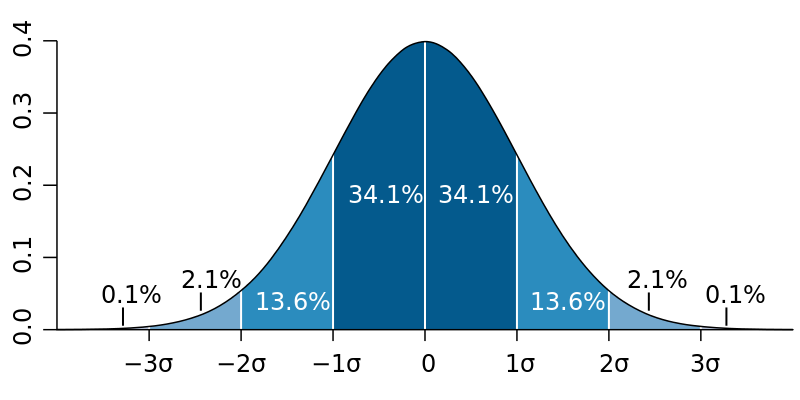
In this figure, the x-axis represents the difference in standard deviations from the mean, while the y-axis represents the percentiles of the data set. On the x-axis, the 0 is the mean. The points to its left are -1, -2, and -3 standard deviations from the mean, and vice versa on the right. This graph tells us that 34.1% of this data set falls between -1 and 1 standard deviation from the mean, while a mere 0.1% falls outside of -3 and 3.
Standard Deviation on the AP® Statistics Test
On the AP® Statistics test, you will be given all the relevant standard deviation formulas on the AP® Stats formula sheet. The questions on the test will ask you to demonstrate your knowledge of standard deviation and interpret it in the context of a practical problem. Often, this means using a given standard deviation to calculate another value in a different formula. Take, for instance, this question from the FRQ portion of the 2009 AP® Stats exam.

Image Source: CollegeBoard
This question asks a student to apply the concept of standard deviation in context to determine other information about the tire treads. The red circle marks the most important information you need for this problem. Once we use the standard deviation to find the 70 th percentile, we can use that answer to solve parts b and c.
First, we need to get the z-score for 70 percent—another calculation which involves the standard deviation. The formula to find the z-score is:
For our example, that gives us:
So for 70 percent, z = 0.52. We already have the standard deviation, so we can plug both values into this formula for calculating percentile:
Written out with the values for this problem, that becomes:
Let’s see how the student in this example used that formula to complete the problem:

Image Source: CollegeBoard
This particular test-taker also underlined the same information that we circled in red above and wrote out the mean, standard deviation, p, and z-score needed to complete the problem. This test-taking strategy lets you organize your thoughts and mark relevant information in a question clearly. It also spells out your process for the examiners, who can follow along with your work.
Wrapping Up Standard Deviation
Standard deviation is one of the most important and frequently used statistics we can find—whether used on its own to tell us something about a data set or as part of an equation to find percentile or other information. As a rule of thumb, remember that high standard deviation means lots of variation from the mean and may be caused by factors such as outliers or a more scattered data set while low standard deviation tends to mean less variation from the mean and a more homogeneous data set.
Let’s put everything into practice. Try this AP® Statistics practice question:
Looking for more AP® Statistics practice?
Check out our other articles on AP® Statistics .
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery of the AP® Statistics.
Start practicing here .
Are you a teacher or administrator interested in boosting AP® Statistics student outcomes?
Learn more about our school licenses here .
Interested in a school license?
Popular posts.

AP® Score Calculators
Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides
The ultimate review guides for AP® subjects to help you plan and structure your prep.


Core Subject Review Guides
Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator
See how scores on each section impacts your overall SAT® score

ACT® Score Calculator
See how scores on each section impacts your overall ACT® score

Grammar Review Hub
Comprehensive review of grammar skills

AP® Posters
Download updated posters summarizing the main topics and structure for each AP® exam.
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.
- The Use of Variance and Standard Deviation for Data Interpretation
The Impact of Variance and Standard Deviation on Data Interpretation

Statistics is an essential field with a profound impact on various academic disciplines and professional domains. Mastery of statistical methods is critical for students who aim to excel academically and make informed decisions based on data. Effectively tackling statistical assignments involves more than just applying formulas; it requires a deep understanding of core concepts and strategies. This blog aims to provide students with a comprehensive guide to navigate statistical assignments successfully, focusing on foundational elements such as variables, measures of location, random sampling, standard error, and confidence intervals.
By delving into these key concepts, students can gain a clearer understanding of how to approach their assignments with greater confidence and precision. Grasping the nature of different types of variables and how they influence data analysis is crucial for selecting appropriate statistical methods. Measures of location, including the mean, median, and mode, offer insights into the central tendencies of data, helping students summarize and interpret complex datasets effectively.
Understanding random sampling is vital for ensuring that a sample accurately represents the broader population, thereby minimizing bias and enhancing the generalizability of results. The standard error provides a measure of the precision of sample estimates, indicating how closely the sample mean reflects the population mean. Finally, confidence intervals offer a range within which the true population parameter is likely to fall, adding an extra layer of reliability to statistical conclusions. By mastering these concepts, students will be better equipped to tackle statistical assignments with greater accuracy, leading to more meaningful and impactful analysis. If you need additional support, expert help can guide you through these concepts and effectively solve your statistics homework , ensuring a thorough understanding and successful completion of your assignments.

Understanding Variables in Statistical Analysis
Variables are the foundation of any statistical analysis. They represent the characteristics or attributes of the subjects being studied. In the context of the provided assignment, the variable of interest is the "distance walked per week" by visually impaired Dutch people. But what exactly is a variable, and why is it important?
Types of Variables
Variables can be broadly categorized into two types: quantitative and qualitative.
- Quantitative Variables: These variables represent numerical values and can be further divided into continuous and discrete variables. Continuous variables, like distance walked per week, can take any value within a given range. In contrast, discrete variables take on specific, distinct values, such as the number of children in a family.
- Qualitative Variables: These variables represent categories or attributes and are not numerical. For example, gender, eye color, and nationality are qualitative variables.
Understanding the type of variable you're working with is crucial because it determines the type of statistical analysis you can perform. In our case, "distance walked per week" is a continuous quantitative variable, which allows for a range of statistical methods to be applied.
Why Understanding Variables Matters
Recognizing the type of variable is important for several reasons:
- Choice of Analysis: The type of variable dictates the statistical methods you can use. For example, mean, median, and mode are commonly used for quantitative variables, while frequencies and proportions are more suitable for qualitative variables.
- Data Collection and Measurement: Understanding variables helps in designing surveys and experiments. For instance, knowing that "distance walked" is a continuous variable informs how you measure and record this data accurately.
- Interpretation of Results: Properly identifying variables ensures that the results of your analysis are interpreted correctly. Misidentifying a variable can lead to incorrect conclusions, which could compromise the validity of your findings.
Practical Tips for Students
- Clarify Variable Types: Always start by identifying whether your variables are quantitative or qualitative, and whether they are continuous or discrete. This will guide your analysis approach.
- Consult Your Assignment Requirements: Ensure that you understand the specific requirements of your assignment regarding the variables. This can help avoid common pitfalls and ensure that you are meeting the expectations of your instructor.
- Use Appropriate Graphical Tools: Utilize histograms, scatter plots, or box plots for quantitative variables and bar charts or pie charts for qualitative variables. These tools provide a visual representation of the data, making it easier to understand and analyze.
Understanding variables in statistical analysis is essential for mastering your assignments and ensuring you can effectively complete your statistical analysis homework. Variables define what is being measured and are classified as qualitative (categorical) or quantitative (numerical). Identifying the type of variable helps in choosing the appropriate analytical methods—qualitative variables might use frequency distributions or chi-square tests, while quantitative variables require measures of central tendency and dispersion. By accurately handling variables, you tailor your analysis to the data and meet assignment requirements, enhancing the accuracy, relevance, and impact of your findings. This leads to valid conclusions and effective communication of results.
Selecting Appropriate Measures of Location
Measures of location, also known as measures of central tendency, are statistical tools used to summarize a set of data by identifying the central point within that dataset. These measures include the mean, median, and mode, each providing different insights into the data distribution. In statistical assignments like the one provided, selecting the appropriate measure of location is crucial for accurately interpreting the data.
Key Measures of Location
- Mean: The mean, or average, is the sum of all data points divided by the number of data points. It is widely used because it considers every value in the dataset, making it sensitive to outliers.
- Median: The median is the middle value in a dataset when the values are arranged in ascending or descending order. It is particularly useful when the data is skewed, as it is not affected by extreme values.
- Mode: The mode is the value that appears most frequently in a dataset. It is the only measure of central tendency that can be used with nominal data, making it useful for qualitative data analysis.
Choosing the Right Measure
The choice of which measure of location to use depends on the characteristics of your data:
- Symmetrical Distribution: If the data is symmetrically distributed (i.e., the distribution is not skewed), the mean is often the best measure of central tendency because it uses all data points.
- Skewed Distribution: In cases where the data is skewed, the median is typically more informative because it is less influenced by outliers and skewed data.
- Multimodal Data: When your data has more than one mode (i.e., it is multimodal), the mode can provide insight into the most common values within the dataset.
Using Graphical Methods
Graphical methods are invaluable for visualizing the distribution of your data and selecting the appropriate measure of location:
- Histograms: A histogram is a bar graph that represents the frequency of data points within specified intervals. It can help you visualize the distribution of your data and identify whether it is symmetrical or skewed, which in turn guides your choice of the measure of central tendency.
- Box Plots: A box plot (or whisker plot) displays the distribution of data based on a five-number summary: minimum, first quartile, median, third quartile, and maximum. Box plots are useful for identifying outliers and understanding the spread of your data, which can influence your choice of the median or mean.
- Analyze Data Distribution: Before choosing a measure of location, analyze the distribution of your data using graphical methods like histograms or box plots.
- Consider Outliers: If your data contains outliers, consider using the median instead of the mean to reduce the impact of these extreme values.
- Report Multiple Measures: In some cases, it may be beneficial to report more than one measure of location to provide a more comprehensive summary of your data.
By understanding and selecting the appropriate measures of location, you can effectively summarize your data and provide meaningful insights in your statistical assignments.
The Significance of Random Sampling in Statistics
Random sampling is a fundamental concept in statistics, ensuring that the sample you collect accurately represents the population you are studying. In the context of the provided assignment, the importance of random sampling cannot be overstated, as it directly impacts the validity and reliability of the results.
What is Random Sampling?
Random sampling is a method where each member of a population has an equal chance of being selected for the sample. This process eliminates selection bias and ensures that the sample is representative of the entire population, allowing for generalizable conclusions.
Types of Random Sampling
There are several methods of random sampling, each with its own advantages:
- Simple Random Sampling: In simple random sampling, every member of the population has an equal chance of being selected. This method is straightforward but requires a complete list of the population, which can be challenging to obtain in large populations.
- Stratified Random Sampling: Stratified sampling involves dividing the population into subgroups (strata) based on specific characteristics, such as age or gender, and then randomly selecting samples from each stratum. This method ensures that different subgroups are adequately represented in the sample.
- Systematic Sampling: In systematic sampling, every nth member of the population is selected after choosing a random starting point. This method is easier to implement than simple random sampling but may introduce bias if there is a hidden pattern in the population list.
Why Random Sampling Matters
Random sampling is crucial for several reasons:
- Reduces Bias: By giving each member of the population an equal chance of selection, random sampling minimizes bias, ensuring that the sample is representative of the population.
- Enhances Validity: A random sample increases the validity of the results by reducing the likelihood that the findings are influenced by a non-representative sample.
- Facilitates Generalization: When a sample is randomly selected, the results can be more confidently generalized to the broader population, making the findings more applicable and meaningful.
Practical Application in the Assignment
In the provided assignment, random sampling was used to select 200 visually impaired Dutch people to study their walking habits. The significance of this random selection lies in its ability to ensure that the sample's walking habits reflect those of the entire population of visually impaired Dutch people, not just a biased subset.
- Understand the Sampling Method: Always clarify the sampling method used in your study. Understanding whether the sample was truly random is essential for interpreting the results accurately.
- Evaluate Sample Representativeness: Consider whether your sample is representative of the population. If the sample is not random, acknowledge this limitation and consider its impact on your findings.
- Use Random Sampling Tools: Utilize tools and software to ensure that your sampling process is truly random. This can include random number generators or specialized statistical software.
Random sampling is a cornerstone of robust statistical analysis. By ensuring that your sample is representative of the population, you can produce more reliable and valid results in your assignments.
The Role of Standard Error in Statistical Analysis
The standard error (SE) is a critical concept in statistics that measures the precision of a sample estimate. Understanding the standard error is essential for interpreting your statistical results and making informed conclusions about the population from which the sample was drawn.
What is Standard Error?
The standard error is the standard deviation of the sampling distribution of a statistic, most commonly the mean. It provides an estimate of the variability of the sample mean if you were to take multiple samples from the same population. The smaller the standard error, the more precise your sample mean is as an estimate of the population mean.
Why Standard Error Matters
The standard error plays a crucial role in several aspects of statistical analysis:
- Confidence Intervals: The standard error is used to calculate confidence intervals, which provide a range of values within which the population mean is likely to fall. A smaller standard error results in a narrower confidence interval, indicating more precise estimates.
- Hypothesis Testing: In hypothesis testing, the standard error is used to determine the significance of the results. A smaller standard error suggests that the sample mean is close to the population mean, increasing the likelihood that observed differences are statistically significant.
- Interpreting Results: Understanding the standard error helps in interpreting the reliability of your results. A larger standard error indicates greater variability and less confidence in the sample mean as an estimate of the population mean.
In the provided assignment, the standard error can be used to assess the reliability of the sample mean distance walked by the 200 visually impaired Dutch people. If the standard error is small, it indicates that the sample mean is a good estimate of the population mean, providing confidence in the results.
- Always Calculate the Standard Error: When reporting the mean of a sample, always include the standard error to provide a measure of precision.
- Use Standard Error to Inform Conclusions: Consider the standard error when interpreting your results. A small standard error suggests that your findings are robust and likely to reflect the true population values.
- Report Confidence Intervals: Alongside the standard error, report confidence intervals to provide a more complete picture of the uncertainty surrounding your estimates.
The standard error is a vital tool for assessing the precision of your statistical estimates. By understanding and correctly interpreting the standard error, you can enhance the credibility and accuracy of your statistical analysis.
Understanding foundational statistical concepts such as variables, measures of location, random sampling, and standard error is crucial for conducting accurate and insightful data analysis. Variables define what you measure and how you analyze it, and recognizing their types helps in selecting appropriate analytical methods. Measures of location, including the mean, median, and mode, provide a summary of central tendencies, distilling complex datasets into understandable figures and revealing underlying trends. Random sampling ensures that your sample represents the broader population accurately, minimizing bias and enhancing the generalizability of your results.
The standard error plays a critical role in assessing the precision of your sample estimates. A smaller standard error indicates that your sample mean is a more accurate reflection of the population mean, which strengthens the credibility of your findings. Reporting the standard error along with confidence intervals gives a fuller picture of the reliability and uncertainty of your results. Mastery of these concepts not only enhances the quality of your data analysis but also ensures that your conclusions are both reliable and impactful.
Post a comment...
The use of variance and standard deviation for data interpretation submit your homework, attached files.
| File | Actions |
|---|

IMAGES
VIDEO
COMMENTS
Learn how to calculate the standard deviation and variance of a data set with Quizlet flashcards. Test your knowledge and improve your statistics skills.
View 1.3.9 Practice- Standard Deviation and Variance.docx from STATS MISC at Florida Virtual School. AP Statistics Assignment: Standard Deviation and Variance Page 1 of 6 Remember that the standard
Therefore, skewness tends to have a more pronounced effect on the standard deviation, as it directly reflects the distribution's asymmetry and the presence of extreme values. 6. A. Range= 88.8-3.0= 85.8 B. Sample Mean: x̄ =68.47 C.Sample Varience=σ^2= 458.82 Standard Deviation= σ=21.42 D. Scenario 1: If the stunted plants are clearly not ...
AP Statistics Worksheets A statistics student's bread and butter: AP Formula Sheet Random Number Table (from textbook) Z-Score Table T-Distribution Table Chi-Square Table ~Below are all of the worksheets that you will get throughout the year~ (if you are missing any, extras are in the AP Statistics binder on the back desk) Basics Quiz (Ch 1.1, 4.1, & 4.2) Is the Airline Discriminating Activity ...
We always calculate variability by summing squared deviations from the mean. That gives us a variance—measured in square units (square dollars, say, whatever those are). We realign the units with the variable by taking the square root of that variance. This gives us the standard deviation (now in dollars again).
Prep for your AP® Stats exam with this crash course in standard deviation: the formula, context, and its role in other statistical calculations.
1) Subtract each value the variable can take and the mean of the variable. 2) Square the difference. 3) Multiply each result by the corresponding probability. 4) Add everything up. Standard deviation of random variable. the square root of the variance. -On calculator press Stat —> Calc —> 1-Var Stats.
Study with Quizlet and memorize flashcards containing terms like Standard deviation, Variance, Bar graph and more.
A sample of size 20 from a normal distribution has sample mean 3.5 and sample variance 14.75. Find 90% confidence intervals for the variance and standard deviation of the distribution.
SC7—The course teaches students how to communicate methods, results and interpretations using the vocabulary of statistics. SC10—The course demonstrates the use of computers and/ or computer output to enhance the development of statistical understanding through exploring data, analyzing data, and/or assessing models.
Statistics document from Excel High School, 5 pages, AP Statistics Assignment: Standard Deviation and Variance Page 2 of 6 For each calculation, use the symbol for the measure you are calculating.
The standard deviation s measures spread about the mean in the original scale. If the variance is the average of the squares of the deviations of the observations from their mean, why do we average by dividing by n - 1 rather than n?
A former high school teacher for 10 years in Kalamazoo, Michigan, Jeff taught Algebra 1, Geometry, Algebra 2, Introductory Statistics, and AP¨_ Statistics.
View 1.3.9 - AP Statistics .pdf from MATH 105 at Forest Hills Central High School. AP Statistics Assignment: Standard Deviation and Variance Situation Sample Std. Deviation Population Std. Formula
AP Statistics Page 2 of 6 Assignment: Standard Deviation and Variance For each calculation, use the symbol for the measure you are calculating. For example, if you're calculating a sample mean, use the symbol x when referring to your answer.
Study with Quizlet and memorize flashcards containing terms like Interpret Standard Deviation, Conditions for Inference for regression, Interpreting a confidence interval and more.
AP® Statistics. AP Statistics gives students hands-on experience collecting, analyzing, graphing, and interpreting real-world data. They will learn to effectively design and analyze research studies by reviewing and evaluating real research examples taken from daily life.
Statistics document from Lone Star College, Tomball, 6 pages, AP Statistics Assignment: Standard Deviation and Variance Page 1 of 6 Remember that the standard deviation and variance can only be used when the mean is used as the measure of center.
Statistics document from University of California, Berkeley, 6 pages, Anvthri Das F/%/23 AP Statistics Assignment: Standard Page 1 of 6 Deviation and Variance Remember that the standard deviation and variance can only be used when the mean is used as the measure of center.
Round your answers to 3 decimal places. (You'll be able to use your calculator on the problems after this one.) (4 points) You are given a sample with measurements: 3, 1, 5, 6, 4, 4, 3, 5. A. Calculate the range (maximum value - minimum value). B. Calculate the sample mean. C. Calculate the sample variance and sample standard deviation.
AP Stats Extra Practice Chapter 6. 44 terms. Hayden_Miller7. Preview. Study with Quizlet and memorize flashcards containing terms like What is a discrete random variable?, Describe a histogram, What is the expected value? and more.
Sally Morton is a seasoned statistics expert with extensive experience in data analysis and statistical interpretation. With a deep understanding of variance, standard deviation, and their applications in real-world data analysis, Sally provides valuable insights and practical guidance for accurate data interpretation.