

Conditional Statement – Definition, Truth Table, Examples, FAQs
What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.
A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics.
Conditional statement symbol : p → q
A conditional statement consists of two parts.
- The “if” clause, which presents a condition or hypothesis.
- The “then” clause, which indicates the consequence or result that follows if the condition is true.
Example : If you brush your teeth, then you won’t get cavities.
Hypothesis (Condition): If you brush your teeth
Conclusion (Consequence): then you won’t get cavities

Recommended Games

Conditional Statement: Definition
A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:
- The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
- The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied.
Recommended Worksheets

More Worksheets
Representation of Conditional Statement
The conditional statement of the form ‘If p, then q” is represented as p → q.
It is pronounced as “p implies q.”
Different ways to express a conditional statement are:
- p implies q
- p is sufficient for q
- q is necessary for p
Parts of a Conditional Statement
There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”
Conditional Statements Examples:
Example 1: If it is Sunday, then you can go to play.
Hypothesis: If it is Sunday
Conclusion: then you can go to play.
Example 2: If you eat all vegetables, then you can have the dessert.
Condition: If you eat all vegetables
Conclusion: then you can have the dessert
To form a conditional statement, follow these concise steps:
Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.
Step 2 : Use the “if… then…” structure to connect the condition and consequence.
Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.
Example 1 : “If you study (condition), then you will pass the exam (consequence).”
This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).
Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.
Hypothesis: If you arrange the numbers from smallest to largest
Conclusion: then you will have an ascending order
Truth Table for Conditional Statement
The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination.
The truth value of p → q is false only when p is true and q is False.
If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.
In all the other cases, it is true.
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements.
Converse, Inverse, and Contrapositive
The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.”
| Conditional Statement | p q |
| Converse | q p |
| Inverse | ~p → ~q |
| Contrapositive | ~q → ~p |
Consider a conditional statement: If I run, then I feel great.
- Converse:
The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.”
Converse: If I feel great, then I run.
- Inverse:
The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”
Inverse : If I don’t run, then I don’t feel great.
- Contrapositive:
The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”
Contrapositive: If I don’t feel great, then I don’t run.
A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”
In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent.
If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false.
Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values.
Examples :
- I will stop my bike if and only if the traffic light is red.
- I will stay if and only if you play my favorite song.
Facts about Conditional Statements
- The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.”
- The conditional statement is not logically equivalent to its converse and inverse.
- The conditional statement is logically equivalent to its contrapositive.
- Thus, we can write p → q ∼q → ∼p
In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.
Example 1: Identify the hypothesis and conclusion.
If you sing, then I will dance.
Solution :
Given statement: If you sing, then I will dance.
Here, the antecedent or the hypothesis is “if you sing.”
The conclusion is “then I will dance.”
Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.”
Here, p: The switch is off
q: The machine won’t work.
The conditional statement can be denoted as p → q.
Converse of p → q is written by reversing the order of p and q in the original statement.
Converse of p → q is q → p.
Converse of p → q: q → p: If the machine won’t work, then the switch is off.
Example 3: What is the truth value of the given conditional statement?
If 2+2=5 , then pigs can fly.
Solution:
q: Pigs can fly.
The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true.
F → F = T
Hence, the truth value of the statement is true.
Conditional Statement - Definition, Truth Table, Examples, FAQs
Attend this quiz & Test your knowledge.
What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.
A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.
What is the meaning of conditional statements?
Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.
When does the truth value of a conditional statement is F?
A conditional statement is considered false when the antecedent is true and the consequent is false.
What is the contrapositive of a conditional statement?
The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.
RELATED POSTS
- Ordering Decimals: Definition, Types, Examples
- Decimal to Octal: Steps, Methods, Conversion Table
- Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
- X Intercept – Definition, Formula, Graph, Examples
- Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Conditional Statement
A conditional statement is a part of mathematical reasoning which is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs need a factual and scientific basis.
Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.

In this mini-lesson, we will explore the world of conditional statements. We will walk through the answers to the questions like what is meant by a conditional statement, what are the parts of a conditional statement, and how to create conditional statements along with solved examples and interactive questions.
Lesson Plan
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What Is Meant By a Conditional Statement?
A statement that is of the form "If p, then q" is a conditional statement. Here 'p' refers to 'hypothesis' and 'q' refers to 'conclusion'.
For example, "If Cliff is thirsty, then she drinks water."

This is a conditional statement. It is also called an implication.
'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B.
Here are two more conditional statement examples
Example 1: If a number is divisible by 4, then it is divisible by 2.
Example 2: If today is Monday, then yesterday was Sunday.
What Are the Parts of a Conditional Statement?
Hypothesis (if) and Conclusion (then) are the two main parts that form a conditional statement.
Let us consider the above-stated example to understand the parts of a conditional statement.
Conditional Statement : If today is Monday, then yesterday was Sunday.
Hypothesis : "If today is Monday."
Conclusion : "Then yesterday was Sunday."
On interchanging the form of statement the relationship gets changed.
To check whether the statement is true or false here, we have subsequent parts of a conditional statement. They are:
- Contrapositive
Biconditional Statement
Let us consider hypothesis as statement A and Conclusion as statement B.
Following are the observations made:
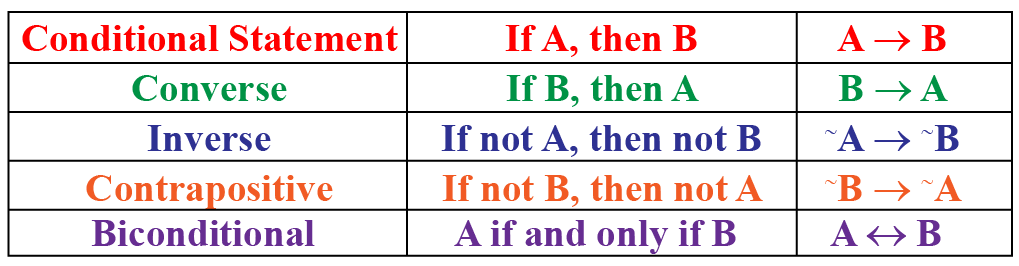
Converse of Statement
When hypothesis and conclusion are switched or interchanged, it is termed as converse statement . For example,
Conditional Statement : “If today is Monday, then yesterday was Sunday.”
Hypothesis : “If today is Monday”
Converse : “If yesterday was Sunday, then today is Monday.”
Here the conditional statement logic is, If B, then A (B → A)
Inverse of Statement
When both the hypothesis and conclusion of the conditional statement are negative, it is termed as an inverse of the statement. For example,
Conditional Statement: “If today is Monday, then yesterday was Sunday”.
Inverse : “If today is not Monday, then yesterday was not Sunday.”
Here the conditional statement logic is, If not A, then not B (~A → ~B)
Contrapositive Statement
When the hypothesis and conclusion are negative and simultaneously interchanged, then the statement is contrapositive. For example,
Contrapositive: “If yesterday was not Sunday, then today is not Monday”
Here the conditional statement logic is, if not B, then not A (~B → ~A)
The statement is a biconditional statement when a statement satisfies both the conditions as true, being conditional and converse at the same time. For example,
Biconditional : “Today is Monday if and only if yesterday was Sunday.”
Here the conditional statement logic is, A if and only if B (A ↔ B)
How to Create Conditional Statements?
Here, the point to be kept in mind is that the 'If' and 'then' part must be true.
If a number is a perfect square , then it is even.
- 'If' part is a number that is a perfect square.
Think of 4 which is a perfect square.
This has become true.
- The 'then' part is that the number should be even. 4 is even.
This has also become true.
Thus, we have set up a conditional statement.
Let us hypothetically consider two statements, statement A and statement B. Observe the truth table for the statements:
|
| ||
| Truth | Truth | Truth |
| Truth | False | False |
| False | Truth | Truth |
| False | False | Truth |
According to the table, only if the hypothesis (A) is true and the conclusion (B) is false then, A → B will be false, or else A → B will be true for all other conditions.

- A sentence needs to be either true or false, but not both, to be considered as a mathematically accepted statement.
- Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement.
- A sentence containing one or many variables is termed as an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values.
Solved Examples
Let us have a look at a few solved examples on conditional statements.
Identify the types of conditional statements.
There are four types of conditional statements:
- If condition
- If-else condition
- Nested if-else
- If-else ladder.
Ray tells "If the perimeter of a rectangle is 14, then its area is 10."
Which of the following could be the counterexamples? Justify your decision.
a) A rectangle with sides measuring 2 and 5
b) A rectangle with sides measuring 10 and 1
c) A rectangle with sides measuring 1 and 5
d) A rectangle with sides measuring 4 and 3
a) Rectangle with sides 2 and 5: Perimeter = 14 and area = 10
Both 'if' and 'then' are true.
b) Rectangle with sides 10 and 1: Perimeter = 22 and area = 10
'If' is false and 'then' is true.
c) Rectangle with sides 1 and 5: Perimeter = 12 and area = 5
Both 'if' and 'then' are false.
d) Rectangle with sides 4 and 3: Perimeter = 14 and area = 12
'If' is true and 'then' is false.
Joe examined the set of numbers {16, 27, 24} to check if they are the multiples of 3. He claimed that they are divisible by 9. Do you agree or disagree? Justify your answer.
Conditional statement : If a number is a multiple of 3, then it is divisible by 9.
Let us find whether the conditions are true or false.
a) 16 is not a multiple of 3. Thus, the condition is false.
16 is not divisible by 9. Thus, the conclusion is false.
b) 27 is a multiple of 3. Thus, the condition is true.
27 is divisible by 9. Thus, the conclusion is true.
c) 24 is a multiple of 3. Thus the condition is true.
24 is not divisible by 9. Thus the conclusion is false.
Write the converse, inverse, and contrapositive statement for the following conditional statement.
If you study well, then you will pass the exam.
The given statement is - If you study well, then you will pass the exam.
It is of the form, "If p, then q"
The converse statement is, "You will pass the exam if you study well" (if q, then p).
The inverse statement is, "If you do not study well then you will not pass the exam" (if not p, then not q).
The contrapositive statement is, "If you did not pass the exam, then you did not study well" (if not q, then not p).
Interactive Questions
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.

Let's Summarize
The mini-lesson targeted the fascinating concept of the conditional statement. The math journey around conditional statements started with what a student already knew and went on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever.
About Cuemath
At Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

FAQs on Conditional Statement
1. what is the most common conditional statement.
'If and then' is the most commonly used conditional statement.
2. When do you use a conditional statement?
Conditional statements are used to justify the given condition or two statements as true or false.
3. What is if and if-else statement?
If is used when a specified condition is true. If-else is used when a particular specified condition is not satisfying and is false.
4. What is the symbol for a conditional statement?
'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B.
5. What is the Contrapositive of a conditional statement?
If not B, then not A (~B → ~A)
6. What is a universal conditional statement?
Conditional statements are those statements where a hypothesis is followed by a conclusion. It is also known as an " If-then" statement. If the hypothesis is true and the conclusion is false, then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false. Conditional statements are also termed as implications.
Conditional Statement: If today is Monday, then yesterday was Sunday
Hypothesis: "If today is Monday."
Conclusion: "Then yesterday was Sunday."
If A, then B (A → B)
- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school
- + ACCUPLACER Mathematics
- + ACT Mathematics
- + AFOQT Mathematics
- + ALEKS Tests
- + ASVAB Mathematics
- + ATI TEAS Math Tests
- + Common Core Math
- + DAT Math Tests
- + FSA Tests
- + FTCE Math
- + GED Mathematics
- + Georgia Milestones Assessment
- + GRE Quantitative Reasoning
- + HiSET Math Exam
- + HSPT Math
- + ISEE Mathematics
- + PARCC Tests
- + Praxis Math
- + PSAT Math Tests
- + PSSA Tests
- + SAT Math Tests
- + SBAC Tests
- + SIFT Math
- + SSAT Math Tests
- + STAAR Tests
- + TABE Tests
- + TASC Math
- + TSI Mathematics
- + ACT Math Worksheets
- + Accuplacer Math Worksheets
- + AFOQT Math Worksheets
- + ALEKS Math Worksheets
- + ASVAB Math Worksheets
- + ATI TEAS 6 Math Worksheets
- + FTCE General Math Worksheets
- + GED Math Worksheets
- + 3rd Grade Mathematics Worksheets
- + 4th Grade Mathematics Worksheets
- + 5th Grade Mathematics Worksheets
- + 6th Grade Math Worksheets
- + 7th Grade Mathematics Worksheets
- + 8th Grade Mathematics Worksheets
- + 9th Grade Math Worksheets
- + HiSET Math Worksheets
- + HSPT Math Worksheets
- + ISEE Middle-Level Math Worksheets
- + PERT Math Worksheets
- + Praxis Math Worksheets
- + PSAT Math Worksheets
- + SAT Math Worksheets
- + SIFT Math Worksheets
- + SSAT Middle Level Math Worksheets
- + 7th Grade STAAR Math Worksheets
- + 8th Grade STAAR Math Worksheets
- + THEA Math Worksheets
- + TABE Math Worksheets
- + TASC Math Worksheets
- + TSI Math Worksheets
- + AFOQT Math Course
- + ALEKS Math Course
- + ASVAB Math Course
- + ATI TEAS 6 Math Course
- + CHSPE Math Course
- + FTCE General Knowledge Course
- + GED Math Course
- + HiSET Math Course
- + HSPT Math Course
- + ISEE Upper Level Math Course
- + SHSAT Math Course
- + SSAT Upper-Level Math Course
- + PERT Math Course
- + Praxis Core Math Course
- + SIFT Math Course
- + 8th Grade STAAR Math Course
- + TABE Math Course
- + TASC Math Course
- + TSI Math Course
- + Number Properties Puzzles
- + Algebra Puzzles
- + Geometry Puzzles
- + Intelligent Math Puzzles
- + Ratio, Proportion & Percentages Puzzles
- + Other Math Puzzles
How to Understand ‘If-Then’ Conditional Statements: A Comprehensive Guide
In math, and even in everyday life, we often say 'if this, then that.' This is the essence of conditional statements. They set up a condition and then describe what happens if that condition is met. For instance, 'If it rains, then the ground gets wet.' These statements are foundational in math, helping us build logical arguments and solve problems. In this guide, we'll dive into the clear-cut world of conditional statements, breaking them down in both simple terms and their mathematical significance.

Step-by-step Guide: Conditional Statements
Defining Conditional Statements: A conditional statement is a logical statement that has two parts: a hypothesis (the ‘if’ part) and a conclusion (the ‘then’ part). Written symbolically, it takes the form: \( \text{If } p, \text{ then } q \) Where \( p \) is the hypothesis and \( q \) is the conclusion.
Truth Values: A conditional statement is either true or false. The only time a conditional statement is false is when the hypothesis is true, but the conclusion is false.
Converse, Inverse, and Contrapositive: 1. Converse: The converse of a conditional statement switches the hypothesis and the conclusion. For the statement “If \( p \), then \( q \)”, the converse is “If \( q \), then \( p \)”.
2. Inverse: The inverse of a conditional statement negates both the hypothesis and the conclusion. For the statement “If \( p \), then \( q \)”, the inverse is “If not \( p \), then not \( q \)”.
3. Contrapositive: The contrapositive of a conditional statement switches and negates both the hypothesis and the conclusion. For the statement “If \( p \), then \( q \)”, the contrapositive is “If not \( q \), then not \( p \)”.
Example 1: Simple Conditional Statement: “If it is raining, then the ground is wet.”
Solution: Hypothesis \(( p )\): It is raining. Conclusion \(( q )\): The ground is wet.
Example 2: Determining Truth Value Statement: “If a shape has four sides, then it is a rectangle.”
Solution: This statement is false because a shape with four sides could be a square, trapezoid, or other quadrilateral, not necessarily a rectangle.
Example 3: Converse, Inverse, and Contrapositive Statement: “If a number is even, then it is divisible by \(2\).”
Solution: Converse: If a number is divisible by \(2\), then it is even. Inverse: If a number is not even, then it is not divisible by \(2\). Contrapositive: If a number is not divisible by \(2\), then it is not even.
Practice Questions:
- Write the converse, inverse, and contrapositive for the statement: “If a bird is a penguin, then it cannot fly.”
- Determine the truth value of the statement: “If a shape has three sides, then it is a triangle.”
- For the statement “If an animal is a cat, then it is a mammal,” which of the following is its converse? a) If an animal is a mammal, then it is a cat. b) If an animal is not a cat, then it is not a mammal. c) If an animal is not a mammal, then it is not a cat.
- Converse: If a bird cannot fly, then it is a penguin. Inverse: If a bird is not a penguin, then it can fly. Contrapositive: If a bird can fly, then it is not a penguin.
- The statement is true. A shape with three sides is defined as a triangle.
- a) If an animal is a mammal, then it is a cat.
by: Effortless Math Team about 1 year ago (category: Articles )
Effortless Math Team
Related to this article, more math articles.
- PSAT 10 Math Formulas
- Top 10 Tips You MUST Know to Retake the ISEE Math
- The Ultimate Accuplacer Math Course (+FREE Worksheets)
- How to Multiply two Binomials Using Algebra Tiles?
- 7th Grade OST Math Practice Test Questions
- Cracking the Case: How to Understand Word Problems of Interpreting a Graph
- How to Get Better at Math: 7 Comprehensive Tips for Parents with Kids Struggling
- How to Add and Subtract Polynomials? (+FREE Worksheet!)
- 8th Grade SBAC Math FREE Sample Practice Questions
- 8th Grade WVGSA Math Worksheets: FREE & Printable
What people say about "How to Understand ‘If-Then’ Conditional Statements: A Comprehensive Guide - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.
Leave a Reply Cancel reply
You must be logged in to post a comment.
Algebra I Study Guide A Comprehensive Review and Step-By-Step Guide to Preparing for Algebra I
Oar math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the oar math, grade 8 math study guide 2021 – 2022 a comprehensive review and step-by-step guide to preparing for grade 8 math, shsat math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the shsat math, hspt math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the hspt math, psat math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the psat math, act math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the act math, pre-algebra study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the pre-algebra, asvab math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the asvab math, dat quantitative reasoning study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the dat quantitative reasoning, chspe math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the chspe math, tsi math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the tsi math, tabe 11 & 12 math study guide 2020 – 2021 for level d a comprehensive review and step-by-step guide to preparing for the tabe math, ftce math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ftce general knowledge math, ged math study guide 2020 – 2021 a comprehensive review and step-by-step guide to preparing for the ged math.
- ATI TEAS 6 Math
- ISEE Upper Level Math
- SSAT Upper-Level Math
- Praxis Core Math
- 8th Grade STAAR Math
Limited time only!
Save Over 45 %
It was $89.99 now it is $49.99
Login and use all of our services.
Effortless Math services are waiting for you. login faster!
Register Fast!
Password will be generated automatically and sent to your email.
After registration you can change your password if you want.
- Math Worksheets
- Math Courses
- Math Topics
- Math Puzzles
- Math eBooks
- GED Math Books
- HiSET Math Books
- ACT Math Books
- ISEE Math Books
- ACCUPLACER Books
- Premium Membership
- Youtube Videos
Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.
- Bulk Orders
- Refund Policy
Calcworkshop
Conditional Statement If Then's Defined in Geometry - 15+ Examples!
// Last Updated: January 21, 2020 - Watch Video //
In today’s geometry lesson , you’re going to learn all about conditional statements!

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)
We’re going to walk through several examples to ensure you know what you’re doing.
In addition, this lesson will prepare you for deductive reasoning and two column proofs later on.
Here we go!
What are Conditional Statements?
To better understand deductive reasoning, we must first learn about conditional statements.
A conditional statement has two parts: hypothesis ( if ) and conclusion ( then ).
In fact, conditional statements are nothing more than “If-Then” statements!
Sometimes a picture helps form our hypothesis or conclusion. Therefore, we sometimes use Venn Diagrams to visually represent our findings and aid us in creating conditional statements.
But to verify statements are correct, we take a deeper look at our if-then statements. This is why we form the converse , inverse , and contrapositive of our conditional statements.
What is the Converse of a Statement?
Well, the converse is when we switch or interchange our hypothesis and conclusion.
Conditional Statement : “If today is Wednesday, then yesterday was Tuesday.”
Hypothesis : “If today is Wednesday” so our conclusion must follow “Then yesterday was Tuesday.”
So the converse is found by rearranging the hypothesis and conclusion, as Math Planet accurately states.
Converse : “If yesterday was Tuesday, then today is Wednesday.”
What is the Inverse of a Statement?
Now the inverse of an If-Then statement is found by negating (making negative) both the hypothesis and conclusion of the conditional statement.
So using our current conditional statement, “If today is Wednesday, then yesterday was Tuesday”.
Inverse : “If today is not Wednesday, then yesterday was not Tuesday.”
What is a Contrapositive?
And the contrapositive is formed by interchanging the hypothesis and conclusion and then negating both.
Contrapositive : “If yesterday was not Tuesday, then today is not Wednesday”
What is a Biconditional Statement?
A statement written in “if and only if” form combines a reversible statement and its true converse. In other words the conditional statement and converse are both true.
Continuing with our initial condition, “If today is Wednesday, then yesterday was Tuesday.”
Biconditional : “Today is Wednesday if and only if yesterday was Tuesday.”

Examples of Conditional Statements
In the video below we will look at several harder examples of how to form a proper statement, converse, inverse, and contrapositive. And here’s a big hint…
Whenever you see “con” that means you switch! It’s like being a con-artist!
Moreover, we will detail the process for coming up with reasons for our conclusions using known postulates. We will review the ten postulates that we have learned so far, and add a few more problems dealing with perpendicular lines, planes, and perpendicular bisectors.
After this lesson, we will be ready to tackle deductive reasoning head-on, and feel confident as we march onward toward learning two-column proofs!
Conditional Statements – Lesson & Examples (Video)
- Introduction to conditional statements
- 00:00:25 – What are conditional statements, converses, and biconditional statements? (Examples #1-2)
- 00:05:21 – Understanding venn diagrams (Examples #3-4)
- 00:11:07 – Supply the missing venn diagram and conditional statement for each question (Examples #5-8)
- Exclusive Content for Member’s Only
- 00:17:48 – Write the statement and converse then determine if they are reversible (Examples #9-12)
- 00:29:17 – Understanding the inverse, contrapositive, and symbol notation
- 00:35:33 – Write the statement, converse, inverse, contrapositive, and biconditional statements for each question (Examples #13-14)
- 00:45:40 – Using geometry postulates to verify statements (Example #15)
- 00:53:23 – What are perpendicular lines, perpendicular planes and the perpendicular bisector?
- 00:56:26 – Using the figure, determine if the statement is true or false (Example #16)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Get My Subscription Now
Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.
Understanding a Conditional Statement
Definition: A Conditional Statement is…
| p | q | p |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Example 1:
| Given: | p: I do my homework. |
| q: I get my allowance. | |
| Problem: | What does p |
Example 2:
| Given: | a: The sun is made of gas. |
| b: 3 is a prime number. | |
| Problem: | Write a |
| a | b | a |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Example 3:
| Given: | x: Gisele has a math assignment. |
| y: David owns a car. | |
| Problem: | Write x |
In the following examples, we are given the truth values of the hypothesis and the conclusion and asked to determine the truth value of the conditional.
Example 4:
| Given: | r: 8 is an odd number. | false |
| s: 9 is composite. | true | |
| Problem: | What is the truth value of r | |
Example 5:
| Given: | r: 8 is an odd number. | false |
| s: 9 is composite. | true | |
| Problem: | What is the truth value of s | |
Example 6:
| Given: | p: 7 = 49. | true |
| q: A rectangle does not have 4 sides. | false | |
| r: Harrison Ford is an American actor. | true | |
| s: A square is not a quadrilateral. | false | |
| Problem: | Write each conditional below as a sentence. Then indicate its truth value. | |
| 1. | p | is equal to 49, then a rectangle does not have 4 sides. | |
| 2. | q | ||
| 3. | p | is equal to 49, then Harrison Ford is an American actor. | |
| 4. | q | ||
| 5. | r | is not equal to 49. | |
| 6. | ~r | is equal to 49. |
Note that in item 5, the conclusion is the negation of p. Also, in item 6, the hypothesis is the negation of r.
Directions: Read each question below. Select your answer by clicking on its button. Feedback to your answer is provided in the RESULTS BOX. If you make a mistake, choose a different button.
| RESULTS BOX: |
IMAGES
VIDEO
COMMENTS
There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part.
A conditional statement (also called an if-then statement) is a statement with a hypothesis followed by a conclusion. The hypothesis is the first, or “if,” part of a conditional statement. The conclusion is the second, or “then,” part of a conditional statement.
The statement \(P\) is called the hypothesis of the conditional statement, and the statement \(Q\) is called the conclusion of the conditional statement. Since conditional statements are probably the most important type of statement in mathematics, we give a more formal definition.
Conditional statements are those statements where a hypothesis is followed by a conclusion. It is also known as an " If-then" statement. If the hypothesis is true and the conclusion is false, then the conditional statement is false.
Defining Conditional Statements: A conditional statement is a logical statement that has two parts: a hypothesis (the ‘if’ part) and a conclusion (the ‘then’ part). Written symbolically, it takes the form: \( \text{If } p, \text{ then } q \) Where \( p \) is the hypothesis and \( q \) is the conclusion. Truth Values: A conditional ...
A conditional statement is an if-then statement connecting a hypothesis (p) and the conclusion (q). If the hypothesis of a statement is represented by p and the conclusion is...
1. Chapter 2.2 Conditional Statements If p and q are statement variables, the conditional of q by p is "If p then q" or "p implies q" and is denoted p !q. It is false when p is true and q is false; otherwise it is true. We call p the hypothesis (or antecedent) of the conditional and q the conclusion (or consequent). p q p !q T T T F F T F F
A conditional statement has two parts: hypothesis (if) and conclusion (then). In fact, conditional statements are nothing more than “If-Then” statements! Sometimes a picture helps form our hypothesis or conclusion.
Summary: A conditional statement, symbolized by p q, is an if-then statement in which p is a hypothesis and q is a conclusion. The conditional is defined to be true unless a true hypothesis leads to a false conclusion.
The part after the "if": you get good grades - is called a hypotheses and the part after the "then" - you will get into a good college - is called a conclusion. Hypotheses followed by a conclusion is called an If-then statement or a conditional statement.