assignment on physical quantity

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

1 Introduction: The Nature of Science and Physics

3 1.2 Physical Quantities and Units

• Perform unit conversions both in the SI and English units
• Explain the most common prefixes in the SI units and be able to write them in scientific notation

The range of objects and phenomena studied in physics is immense. From the incredibly short lifetime of a nucleus to the age of the Earth, from the tiny sizes of sub-nuclear particles to the vast distance to the edges of the known universe, from the force exerted by a jumping flea to the force between Earth and the Sun, there are enough factors of 10 to challenge the imagination of even the most experienced scientist. Giving numerical values for physical quantities and equations for physical principles allows us to understand nature much more deeply than does qualitative description alone. To comprehend these vast ranges, we must also have accepted units in which to express them. And we shall find that (even in the potentially mundane discussion of meters, kilograms, and seconds) a profound simplicity of nature appears—all physical quantities can be expressed as combinations of only four fundamental physical quantities: length, mass, time, and electric current.

We define a physical quantity either by specifying how it is measured or by stating how it is calculated from other measurements. For example, we define distance and time by specifying methods for measuring them, whereas we define average speed by stating that it is calculated as distance traveled divided by time of travel.

Measurements of physical quantities are expressed in terms of units , which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in units of meters (for sprinters) or kilometers (for distance runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way. (See Figure 2 . )

There are two major systems of units used in the world: SI units (also known as the metric system) and English units (also known as the customary or imperial system). English units were historically used in nations once ruled by the British Empire and are still widely used in the United States. Virtually every other country in the world now uses SI units as the standard; the metric system is also the standard system agreed upon by scientists and mathematicians. The acronym “SI” is derived from the French Système International .

SI Units: Fundamental and Derived Units

Table 1 gives the fundamental SI units that are used throughout this textbook. This text uses non-SI units in a few applications where they are in very common use, such as the measurement of blood pressure in millimeters of mercury (mm Hg). Whenever non-SI units are discussed, they will be tied to SI units through conversions.

It is an intriguing fact that some physical quantities are more fundamental than others and that the most fundamental physical quantities can be defined only in terms of the procedure used to measure them. The units in which they are measured are thus called fundamental units . In this textbook, the fundamental physical quantities are taken to be length, mass, time, and electric current. (Note that electric current will not be introduced until much later in this text.) All other physical quantities, such as force and electric charge, can be expressed as algebraic combinations of length, mass, time, and current (for example, speed is length divided by time); these units are called derived units .

Units of Time, Length, and Mass: The Second, Meter, and Kilogram

The SI unit for time, the second (abbreviated s), has a long history. For many years it was defined as 1/86,400 of a mean solar day. More recently, a new standard was adopted to gain greater accuracy and to define the second in terms of a non-varying, or constant, physical phenomenon (because the solar day is getting longer due to very gradual slowing of the Earth’s rotation). Cesium atoms can be made to vibrate in a very steady way, and these vibrations can be readily observed and counted. In 1967 the second was redefined as the time required for 9,192,631,770 of these vibrations. (See Figure 3 .) Accuracy in the fundamental units is essential, because all measurements are ultimately expressed in terms of fundamental units and can be no more accurate than are the fundamental units themselves.

The SI unit for length is the meter (abbreviated m); its definition has also changed over time to become more accurate and precise. The meter was first defined in 1791 as 1/10,000,000 of the distance from the equator to the North Pole. This measurement was improved in 1889 by redefining the meter to be the distance between two engraved lines on a platinum-iridium bar now kept near Paris. By 1960, it had become possible to define the meter even more accurately in terms of the wavelength of light, so it was again redefined as 1,650,763.73 wavelengths of orange light emitted by krypton atoms. In 1983, the meter was given its present definition (partly for greater accuracy) as the distance light travels in a vacuum in 1/299,792,458 of a second. (See Figure 4 .) This change defines the speed of light to be exactly 299,792,458 meters per second. The length of the meter will change if the speed of light is someday measured with greater accuracy.

The Kilogram

The SI unit for mass is the kilogram (abbreviated kg); it is defined to be the mass of a platinum-iridium cylinder kept with the old meter standard at the International Bureau of Weights and Measures near Paris. Exact replicas of the standard kilogram are also kept at the United States’ National Institute of Standards and Technology, or NIST, located in Gaithersburg, Maryland outside of Washington D.C., and at other locations around the world. The determination of all other masses can be ultimately traced to a comparison with the standard mass.

Electric current and its accompanying unit, the ampere, will be introduced in Chapter 20 Introduction to Electric Current, Resistance, and Ohm’s Law when electricity and magnetism are covered. The initial modules in this textbook are concerned with mechanics, fluids, heat, and waves. In these subjects all pertinent physical quantities can be expressed in terms of the fundamental units of length, mass, and time.

Metric Prefixes

SI units are part of the metric system . The metric system is convenient for scientific and engineering calculations because the units are categorized by factors of 10. Table 2 gives metric prefixes and symbols used to denote various factors of 10.

Metric systems have the advantage that conversions of units involve only powers of 10. There are 100 centimeters in a meter, 1000 meters in a kilometer, and so on. In nonmetric systems, such as the system of U.S. customary units, the relationships are not as simple—there are 12 inches in a foot, 5280 feet in a mile, and so on. Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by using an appropriate metric prefix. For example, distances in meters are suitable in construction, while distances in kilometers are appropriate for air travel, and the tiny measure of nanometers are convenient in optical design. With the metric system there is no need to invent new units for particular applications.

The term order of magnitude refers to the scale of a value expressed in the metric system. Each power of 10 in the metric system represents a different order of magnitude. For example,[latex]\bf{10^1}[/latex],[latex]\bf{10^2}[/latex],[latex]\bf{10^3}[/latex], and so forth are all different orders of magnitude. All quantities that can be expressed as a product of a specific power of[latex]\bf{10}[/latex] are said to be of the same order of magnitude. For example, the number[latex]\bf{800}[/latex]can be written as[latex]\bf{8\times10^2}[/latex], and the number[latex]\bf{450}[/latex]can be written as[latex]\bf{4.5\times10^2}[/latex] . Thus, the numbers[latex]\bf{800}[/latex]and[latex]\bf{450}[/latex]are of the same order of magnitude:[latex]\bf{10^2}[/latex] . Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of[latex]\bf{10^{-9}}\textbf{ m}[/latex] , while the diameter of the Sun is on the order of[latex]\bf{10^9}\textbf{ m}[/latex].

THE QUEST FOR MICROSCOPIC STANDARDS FOR BASIC UNITS

The fundamental units described in this chapter are those that produce the greatest accuracy and precision in measurement. There is a sense among physicists that, because there is an underlying microscopic substructure to matter, it would be most satisfying to base our standards of measurement on microscopic objects and fundamental physical phenomena such as the speed of light. A microscopic standard has been accomplished for the standard of time, which is based on the oscillations of the cesium atom.

The standard for length was once based on the wavelength of light (a small-scale length) emitted by a certain type of atom, but it has been supplanted by the more precise measurement of the speed of light. If it becomes possible to measure the mass of atoms or a particular arrangement of atoms such as a silicon sphere to greater precision than the kilogram standard, it may become possible to base mass measurements on the small scale. There are also possibilities that electrical phenomena on the small scale may someday allow us to base a unit of charge on the charge of electrons and protons, but at present current and charge are related to large-scale currents and forces between wires.

Known Ranges of Length, Mass, and Time

The vastness of the universe and the breadth over which physics applies are illustrated by the wide range of examples of known lengths, masses, and times in Table 3 . Examination of this table will give you some feeling for the range of possible topics and numerical values. (See Figure 5 and Figure 6 .)

Unit Conversion and Dimensional Analysis

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook, some quantities may be expressed in units of liters and you need to convert them to cups. Or, perhaps you are reading walking directions from one location to another and you are interested in how many miles you will be walking. In this case, you will need to convert units of feet to miles.

Let us consider a simple example of how to convert units. Let us say that we want to convert 80 meters (m) to kilometers (km).

The first thing to do is to list the units that you have and the units that you want to convert to. In this case, we have units in meters and we want to convert to kilometers .

Next, we need to determine a conversion factor relating meters to kilometers. A conversion factor is a ratio expressing how many of one unit are equal to another unit. For example, there are 12 inches in 1 foot, 100 centimeters in 1 meter, 60 seconds in 1 minute, and so on. In this case, we know that there are 1,000 meters in 1 kilometer.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor so that the units cancel out, as shown:

Note that the unwanted m unit cancels, leaving only the desired km unit. You can use this method to convert between any types of unit.

Click Appendix C Useful Information for a more complete list of conversion factors.

Example 1: Unit Conversions: A Short Drive Home

Suppose that you drive the 10.0 km from your university to home in 20.0 min. Calculate your average speed (a) in kilometers per hour (km/h) and (b) in meters per second (m/s). (Note: Average speed is distance traveled divided by time of travel.)

First we calculate the average speed using the given units. Then we can get the average speed into the desired units by picking the correct conversion factor and multiplying by it. The correct conversion factor is the one that cancels the unwanted unit and leaves the desired unit in its place.

Solution for (a)

(1) Calculate average speed. Average speed is distance traveled divided by time of travel. (Take this definition as a given for now—average speed and other motion concepts will be covered in a later module.) In equation form,

(2) Substitute the given values for distance and time.

(3) Convert km/min to km/h: multiply by the conversion factor that will cancel minutes and leave hours. That conversion factor is[latex]\bf{60\textbf{ min/hr}}[/latex]. Thus,

Discussion for (a)

To check your answer, consider the following:

(1) Be sure that you have properly cancelled the units in the unit conversion. If you have written the unit conversion factor upside down, the units will not cancel properly in the equation. If you accidentally get the ratio upside down, then the units will not cancel; rather, they will give you the wrong units as follows:

which are obviously not the desired units of km/h.

(2) Check that the units of the final answer are the desired units. The problem asked us to solve for average speed in units of km/h and we have indeed obtained these units.

(3) Check the significant figures. Because each of the values given in the problem has three significant figures, the answer should also have three significant figures. The answer[latex]30.0 \frac {km} {hr}[/latex] does indeed have three significant figures, so this is appropriate. Note that the significant figures in the conversion factor are not relevant because an hour is defined to be 60 minutes, so the precision of the conversion factor is perfect.

(4) Next, check whether the answer is reasonable. Let us consider some information from the problem—if you travel 10 km in a third of an hour (20 min), you would travel three times that far in an hour. The answer does seem reasonable.

Solution for (b)

There are several ways to convert the average speed into meters per second.

(1) Start with the answer to (a) and convert km/h to m/s. Two conversion factors are needed—one to convert hours to seconds, and another to convert kilometers to meters.

(2) Multiplying by these yields

Discussion for (b)

If we had started with 0.500 km/min, we would have needed different conversion factors, but the answer would have been the same: 8.33 m/s.

You may have noted that the answers in the worked example just covered were given to three digits. Why? When do you need to be concerned about the number of digits in something you calculate? Why not write down all the digits your calculator produces? The module Chapter 1.3 Accuracy, Precision, and Significant Figures will help you answer these questions.

NONSTANDARD UNITS

While there are numerous types of units that we are all familiar with, there are others that are much more obscure. For example, a firkin is a unit of volume that was once used to measure beer. One firkin equals about 34 liters. To learn more about nonstandard units, use a dictionary or encyclopedia to research different “weights and measures.” Take note of any unusual units, such as a barleycorn, that are not listed in the text. Think about how the unit is defined and state its relationship to SI units.

Check Your Understanding 1

1: Some hummingbirds beat their wings more than 50 times per second. A scientist is measuring the time it takes for a hummingbird to beat its wings once. Which fundamental unit should the scientist use to describe the measurement? Which factor of 10 is the scientist likely to use to describe the motion precisely? Identify the metric prefix that corresponds to this factor of 10.

Check Your Understanding 2

1: One cubic centimeter is equal to one milliliter. What does this tell you about the different units in the SI metric system?

• Physical quantities are a characteristic or property of an object that can be measured or calculated from other measurements.
• Units are standards for expressing and comparing the measurement of physical quantities. All units can be expressed as combinations of four fundamental units.
• The four fundamental units we will use in this text are the meter (for length), the kilogram (for mass), the second (for time), and the ampere (for electric current). These units are part of the metric system, which uses powers of 10 to relate quantities over the vast ranges encountered in nature.
• The four fundamental units are abbreviated as follows: meter, m; kilogram, kg; second, s; and ampere, A. The metric system also uses a standard set of prefixes to denote each order of magnitude greater than or lesser than the fundamental unit itself.
• Unit conversions involve changing a value expressed in one type of unit to another type of unit. This is done by using conversion factors, which are ratios relating equal quantities of different units.

Conceptual Questions

1: Identify some advantages of metric units.

Problems & Exercises

1:  The speed limit on some interstate highways is roughly 100 km/h. (a) What is this in meters per second? (b) How many miles per hour is this?

2:  A car is traveling at a speed of[latex]\bf{33\textbf{ m/s.}}[/latex](a) What is its speed in kilometers per hour? (b) Is it exceeding the[latex]\bf{90\textbf{ km/h}}[/latex]speed limit?

3:  Show that[latex]\bf{1.0\textbf{ m/s}=3.6\textbf{ km/h.}}[/latex]Hint: Show the explicit steps involved in converting[latex]\bf{1.0\textbf{ m/s}=3.6\textbf{ km/h.}}[/latex]

4:  American football is played on a 100-yd-long field, excluding the end zones. How long is the field in meters? (Assume that 1 meter equals 3.281 feet.)

5:  Soccer fields vary in size. A large soccer field is 115 m long and 85 m wide. What are its dimensions in feet and inches? (Assume that 1 meter equals 3.281 feet.)

6:  What is the height in meters of a person who is 6 ft 1.0 in. tall? (Assume that 1 meter equals 39.37 in.)

7:  Mount Everest, at 29,028 feet, is the tallest mountain on the Earth. What is its height in kilometers? (Assume that 1 kilometer equals 3,281 feet.)

8:  The speed of sound is measured to be[latex]\bf{342\textbf{ m/s}}[/latex]on a certain day. What is this in km/h?

9:  Tectonic plates are large segments of the Earth’s crust that move slowly. Suppose that one such plate has an average speed of 4.0 cm/year. (a) What distance does it move in 1 s at this speed? (b) What is its speed in kilometers per million years?

10:  (a) Refer to Table 3 to determine the average distance between the Earth and the Sun. Then calculate the average speed of the Earth in its orbit in kilometers per second. (b) What is this in meters per second?

1: The scientist will measure the time between each movement using the fundamental unit of seconds. Because the wings beat so fast, the scientist will probably need to measure in milliseconds, or[latex]\bf{10^{-3}}[/latex]seconds. (50 beats per second corresponds to 20 milliseconds per beat.)

1: The fundamental unit of length (meter) is probably used to create the derived unit of volume (liter). The measure of a milliliter is dependent on the measure of a centimeter.

• [latex]\bf{27.8\textbf{ m/s}}[/latex]
• [latex]\bf{62.1\textbf{ mph}}[/latex]

[latex]\bf{\frac{1.0\textbf{ m}}{s}=\frac{1.0\textbf{ m}}{s}\times\frac{3600\textbf{ s}}{1\textbf{ hr}}\times\frac{1\textbf{ km}}{1000\textbf{ m}}}[/latex]

[latex]\bf{=3.6\textbf{ km/h.}}[/latex]

length:[latex]\bf{377\textbf{ ft;}\: 4.53\times 10^3\textbf{ in.}}[/latex]width:[latex]\bf{280\textbf{ ft;} \; 3.3\times 10^3\textbf{ in.}}[/latex]

[latex]\bf{8.847\textbf{ km}}[/latex]

(a)[latex]\bf{1.3\times10^{-9}\textbf{ m}}[/latex]

(b)[latex]\bf{40\textbf{ km/My}}[/latex]

College Physics chapters 1-17 Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

1.3 The Language of Physics: Physical Quantities and Units

Section learning objectives.

By the end of this section, you will be able to do the following:

• Associate physical quantities with their International System of Units (SI)and perform conversions among SI units using scientific notation
• Relate measurement uncertainty to significant figures and apply the rules for using significant figures in calculations
• Correctly create, label, and identify relationships in graphs using mathematical relationships (e.g., slope, y -intercept, inverse, quadratic and logarithmic)

Teacher Support

The learning objectives in this section will help your students master the following standards:

• (H) make measurements with accuracy and precision and record data using scientific notation and International System (SI) units;
• (L) express and manipulate relationships among physical variables quantitatively, including the use of graphs, charts, and equations.

In addition, the High School Physics Laboratory Manual addresses content in this section in the lab titled: Measurement, Precision and Accuracy, as well as the following standards:

• (I) identify and quantify causes and effects of uncertainties in measured data;
• (J) organize and evaluate data and make inferences from data, including the use of tables, charts, and graphs.

Section Key Terms

[OL] Pre-assessment for this section could involve asking students what experience they have had with the four fundamental units in their daily lives. One could also poll the class for what they think accuracy, precision, and uncertainty refer to. For graphing, students could make a quick graph of some data and then edit their graph after reading to note ways they could improve the clarity of their graph.

The Role of Units

Physicists, like other scientists, make observations and ask basic questions. For example, how big is an object? How much mass does it have? How far did it travel? To answer these questions, they make measurements with various instruments (e.g., meter stick, balance, stopwatch, etc.).

The measurements of physical quantities are expressed in terms of units, which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in meters (for sprinters) or kilometers (for long distance runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way ( Figure 1.13 ).

All physical quantities in the International System of Units (SI) are expressed in terms of combinations of seven fundamental physical units, which are units for: length, mass, time, electric current, temperature, amount of a substance, and luminous intensity.

SI Units: Fundamental and Derived Units

In any system of units, the units for some physical quantities must be defined through a measurement process. These are called the base quantities for that system and their units are the system’s base units . All other physical quantities can then be expressed as algebraic combinations of the base quantities. Each of these physical quantities is then known as a derived quantity and each unit is called a derived unit . The choice of base quantities is somewhat arbitrary, as long as they are independent of each other and all other quantities can be derived from them. Typically, the goal is to choose physical quantities that can be measured accurately to a high precision as the base quantities. The reason for this is simple. Since the derived units can be expressed as algebraic combinations of the base units, they can only be as accurate and precise as the base units from which they are derived.

[OL] As a clarification, certain countries use the British system for a few of their measurements. For example, Britain still uses the pint to measure beer, miles to measure road distances, and pounds to measure body weight (although weight must be reported in kg in British medical records). The British people still use the British system extensively in their everyday lives, but the metric system is the official standard for the government. Likewise, many oil-producing countries measure oil in British gallons.

Based on such considerations, the International Standards Organization recommends using seven base quantities, which form the International System of Quantities (ISQ). These are the base quantities used to define the SI base units. ( Table 1.1 ) lists these seven ISQ base quantities and the corresponding SI base units.

The SI unit for length is the meter (m). The definition of the meter has changed over time to become more accurate and precise. The meter was first defined in 1791 as 1/10,000,000 of the distance from the equator to the North Pole. This measurement was improved in 1889 by redefining the meter to be the distance between two engraved lines on a platinum-iridium bar. (The bar is now housed at the International Bureau of Weights and Measures, near Paris). By 1960, some distances could be measured more precisely by comparing them to wavelengths of light. The meter was redefined as 1,650,763.73 wavelengths of orange light emitted by krypton atoms. In 1983, the meter was given its present definition as the distance light travels in a vacuum in 1/ 299,792,458 of a second ( Figure 1.14 ).

The Kilogram

The SI unit for mass is the kilogram (abbreviated kg); it was previously defined to be the mass of a platinum-iridium cylinder kept with the old meter standard at the International Bureau of Weights and Measures near Paris. Exact replicas of the previously defined kilogram are also kept at the United States’ National Institute of Standards and Technology, or NIST, located in Gaithersburg, Maryland outside of Washington D.C., and at other locations around the world. The determination of all other masses could be ultimately traced to a comparison with the standard mass. Even though the platinum-iridium cylinder was resistant to corrosion, airborne contaminants were able to adhere to its surface, slightly changing its mass over time. In May 2019, the scientific community adopted a more stable definition of the kilogram. The kilogram is now defined in terms of the second, the meter, and Planck's constant, h (a quantum mechanical value that relates a photon's energy to its frequency).

The SI unit for time, the second (s) also has a long history. For many years it was defined as 1/86,400 of an average solar day. However, the average solar day is actually very gradually getting longer due to gradual slowing of Earth’s rotation. Accuracy in the fundamental units is essential, since all other measurements are derived from them. Therefore, a new standard was adopted to define the second in terms of a non-varying, or constant, physical phenomenon. One constant phenomenon is the very steady vibration of Cesium atoms, which can be observed and counted. This vibration forms the basis of the cesium atomic clock . In 1967, the second was redefined as the time required for 9,192,631,770 Cesium atom vibrations ( Figure 1.15 ).

[BL] An average solar day was used to originally define the second because the length of a solar day varies throughout the year due to Earth’s tilt of its axis as well as its elliptical orbit. The accumulation of these variations could result in a day length difference of up to 16 minutes during different seasons. Using an average solar day resolves these variations in day length.

Electric current is measured in the ampere (A), named after Andre Ampere. You have probably heard of amperes, or amps , when people discuss electrical currents or electrical devices. Understanding an ampere requires a basic understanding of electricity and magnetism, something that will be explored in depth in later chapters of this book. Basically, two parallel wires with an electric current running through them will produce an attractive force on each other. One ampere is defined as the amount of electric current that will produce an attractive force of 2.7 × × 10 –7 newton per meter of separation between the two wires (the newton is the derived unit of force).

[BL] Some students may not know that a vacuum is a region of space that contains no air.

The SI unit of temperature is the kelvin (or kelvins, but not degrees kelvin). This scale is named after physicist William Thomson, Lord Kelvin, who was the first to call for an absolute temperature scale. The Kelvin scale is based on absolute zero. This is the point at which all thermal energy has been removed from all atoms or molecules in a system. This temperature, 0 K, is equal to −273.15 °C and −459.67 °F. Conveniently, the Kelvin scale actually changes in the same way as the Celsius scale. For example, the freezing point (0 °C) and boiling points of water (100 °C) are 100 degrees apart on the Celsius scale. These two temperatures are also 100 kelvins apart (freezing point = 273.15 K; boiling point = 373.15 K).

Metric Prefixes

Physical objects or phenomena may vary widely. For example, the size of objects varies from something very small (like an atom) to something very large (like a star). Yet the standard metric unit of length is the meter. So, the metric system includes many prefixes that can be attached to a unit. Each prefix is based on factors of 10 (10, 100, 1,000, etc., as well as 0.1, 0.01, 0.001, etc.). Table 1.2 gives the metric prefixes and symbols used to denote the different various factors of 10 in the metric system.

The metric system is convenient because conversions between metric units can be done simply by moving the decimal place of a number. This is because the metric prefixes are sequential powers of 10. There are 100 centimeters in a meter, 1000 meters in a kilometer, and so on. In nonmetric systems, such as U.S. customary units , the relationships are less simple—there are 12 inches in a foot, 5,280 feet in a mile, 4 quarts in a gallon, and so on. Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by switching to the most-appropriate metric prefix. For example, distances in meters are suitable for building construction, but kilometers are used to describe road construction. Therefore, with the metric system, there is no need to invent new units when measuring very small or very large objects—you just have to move the decimal point (and use the appropriate prefix).

Known Ranges of Length, Mass, and Time

Table 1.3 lists known lengths, masses, and time measurements. You can see that scientists use a range of measurement units. This wide range demonstrates the vastness and complexity of the universe, as well as the breadth of phenomena physicists study. As you examine this table, note how the metric system allows us to discuss and compare an enormous range of phenomena, using one system of measurement ( Figure 1.16 and Figure 1.17 ).

Using Scientific Notation with Physical Measurements

Scientific notation is a way of writing numbers that are too large or small to be conveniently written as a decimal. For example, consider the number 840,000,000,000,000. It’s a rather large number to write out. The scientific notation for this number is 8.40 × × 10 14 . Scientific notation follows this general format

In this format x is the value of the measurement with all placeholder zeros removed. In the example above, x is 8.4. The x is multiplied by a factor, 10 y , which indicates the number of placeholder zeros in the measurement. Placeholder zeros are those at the end of a number that is 10 or greater, and at the beginning of a decimal number that is less than 1. In the example above, the factor is 10 14 . This tells you that you should move the decimal point 14 positions to the right, filling in placeholder zeros as you go. In this case, moving the decimal point 14 places creates only 13 placeholder zeros, indicating that the actual measurement value is 840,000,000,000,000.

Numbers that are fractions can be indicated by scientific notation as well. Consider the number 0.0000045. Its scientific notation is 4.5 × × 10 –6 . Its scientific notation has the same format

Here, x is 4.5. However, the value of y in the 10 y factor is negative, which indicates that the measurement is a fraction of 1. Therefore, we move the decimal place to the left, for a negative y . In our example of 4.5 × × 10 –6 , the decimal point would be moved to the left six times to yield the original number, which would be 0.0000045.

The term order of magnitude refers to the power of 10 when numbers are expressed in scientific notation. Quantities that have the same power of 10 when expressed in scientific notation, or come close to it, are said to be of the same order of magnitude. For example, the number 800 can be written as 8 × × 10 2 , and the number 450 can be written as 4.5 × × 10 2 . Both numbers have the same value for y . Therefore, 800 and 450 are of the same order of magnitude. Similarly, 101 and 99 would be regarded as the same order of magnitude, 10 2 . Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of 10 −9 m, while the diameter of the sun is on the order of 10 9 m. These two values are 18 orders of magnitude apart.

Scientists make frequent use of scientific notation because of the vast range of physical measurements possible in the universe, such as the distance from Earth to the moon ( Figure 1.18 ), or to the nearest star.

Unit Conversion and Dimensional Analysis

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook in the United States, some quantities may be expressed in liters and you need to convert them to cups. A Canadian tourist driving through the United States might want to convert miles to kilometers, to have a sense of how far away his next destination is. A doctor in the United States might convert a patient’s weight in pounds to kilograms.

Let’s consider a simple example of how to convert units within the metric system. How can we convert 1 hour to seconds?

First, we need to determine a conversion factor. A conversion factor is a ratio expressing how many of one unit are equal to another unit. A conversion factor is simply a fraction which equals 1. You can multiply any number by 1 and get the same value. When you multiply a number by a conversion factor, you are simply multiplying it by one. For example, the following are conversion factors: (1 foot)/(12 inches) = 1 to convert inches to feet, (1 meter)/(100 centimeters) = 1 to convert centimeters to meters, (1 minute)/(60 seconds) = 1 to convert seconds to minutes.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor (1 km/1,000m) = 1, so we are simply multiplying 80m by 1:

When there is a unit in the original number, and a unit in the denominator (bottom) of the conversion factor, the units cancel. In this case, hours and minutes cancel and the value in seconds remains.

You can use this method to convert between any types of unit, including between the U.S. customary system and metric system. Notice also that, although you can multiply and divide units algebraically, you cannot add or subtract different units. An expression like 10 km + 5 kg makes no sense. Even adding two lengths in different units, such as 10 km + 20 m does not make sense. You express both lengths in the same unit. See Reference Tables for a more complete list of conversion factors.

Worked Example

Unit conversions: a short drive home.

Suppose that you drive the 10.0 km from your university to home in 20.0 min. Calculate your average speed (a) in kilometers per hour (km/h) and (b) in meters per second (m/s). (Note—Average speed is distance traveled divided by time of travel.)

First we calculate the average speed using the given units. Then we can get the average speed into the desired units by picking the correct conversion factor and multiplying by it. The correct conversion factor is the one that cancels the unwanted unit and leaves the desired unit in its place.

Calculate average speed. Average speed is distance traveled divided by time of travel. (Take this definition as a given for now—average speed and other motion concepts will be covered in a later module.) In equation form,

Substitute the given values for distance and time.

Convert km/min to km/h: multiply by the conversion factor that will cancel minutes and leave hours. That conversion factor is 60 min/1 h 60 min/1 h . Thus,

To check your answer, consider the following:

Be sure that you have properly cancelled the units in the unit conversion. If you have written the unit conversion factor upside down, the units will not cancel properly in the equation. If you accidentally get the ratio upside down, then the units will not cancel; rather, they will give you the wrong units as follows

which are obviously not the desired units of km/h.

• Check that the units of the final answer are the desired units. The problem asked us to solve for average speed in units of km/h and we have indeed obtained these units.
• Check the significant figures. Because each of the values given in the problem has three significant figures, the answer should also have three significant figures. The answer 30.0 km/h does indeed have three significant figures, so this is appropriate. Note that the significant figures in the conversion factor are not relevant because an hour is defined to be 60 min, so the precision of the conversion factor is perfect.
• Next, check whether the answer is reasonable. Let us consider some information from the problem—if you travel 10 km in a third of an hour (20 min), you would travel three times that far in an hour. The answer does seem reasonable.

There are several ways to convert the average speed into meters per second.

• Start with the answer to (a) and convert km/h to m/s. Two conversion factors are needed—one to convert hours to seconds, and another to convert kilometers to meters.

Multiplying by these yields

If we had started with 0.500 km/min, we would have needed different conversion factors, but the answer would have been the same: 8.33 m/s.

You may have noted that the answers in the worked example just covered were given to three digits. Why? When do you need to be concerned about the number of digits in something you calculate? Why not write down all the digits your calculator produces?

Using Physics to Evaluate Promotional Materials

A commemorative coin that is 2″ in diameter is advertised to be plated with 15 mg of gold. If the density of gold is 19.3 g/cc, and the amount of gold around the edge of the coin can be ignored, what is the thickness of the gold on the top and bottom faces of the coin?

To solve this problem, the volume of the gold needs to be determined using the gold’s mass and density. Half of that volume is distributed on each face of the coin, and, for each face, the gold can be represented as a cylinder that is 2″ in diameter with a height equal to the thickness. Use the volume formula for a cylinder to determine the thickness.

The mass of the gold is given by the formula m = ρ V = 15 × 10 − 3 g, m = ρ V = 15 × 10 − 3 g, where ρ = 19.3 g/cc ρ = 19.3 g/cc and V is the volume. Solving for the volume gives V = m ρ = 15 × 10 − 3 g 19.3 g/cc ≅ 7.8 × 10 − 4 cc. V = m ρ = 15 × 10 − 3 g 19.3 g/cc ≅ 7.8 × 10 − 4 cc.

If t is the thickness, the volume corresponding to half the gold is 1 2 ( 7.8 × 10 − 4 ) = π r 2 t = π ( 2.54 ) 2 t, 1 2 ( 7.8 × 10 − 4 ) = π r 2 t = π ( 2.54 ) 2 t, where the 1″ radius has been converted to cm. Solving for the thickness gives t = ( 3.9 × 10 − 4 ) π ( 2.54 ) 2 ≅ 1.9 × 10 − 5 cm = 0.00019 mm. t = ( 3.9 × 10 − 4 ) π ( 2.54 ) 2 ≅ 1.9 × 10 − 5 cm = 0.00019 mm.

The amount of gold used is stated to be 15 mg, which is equivalent to a thickness of about 0.00019 mm. The mass figure may make the amount of gold sound larger, both because the number is much bigger (15 versus 0.00019), and because people may have a more intuitive feel for how much a millimeter is than for how much a milligram is. A simple analysis of this sort can clarify the significance of claims made by advertisers.

Ask students to find other promotional materials that make claims that can be analyzed using physics principles. Compile any items that come in for later use at appropriate points in the course. For example, after covering power consumption in electric circuits, compare the performance of electric fireplaces advertised as revolutionary to the performance of standard space heaters.

Accuracy, Precision and Significant Figures

Science is based on experimentation that requires good measurements. The validity of a measurement can be described in terms of its accuracy and its precision (see Figure 1.19 and Figure 1.20 ). Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard piece of printer paper. The packaging in which you purchased the paper states that it is 11 inches long, and suppose this stated value is correct. You measure the length of the paper three times and obtain the following measurements: 11.1 inches, 11.2 inches, and 10.9 inches. These measurements are quite accurate because they are very close to the correct value of 11.0 inches. In contrast, if you had obtained a measurement of 12 inches, your measurement would not be very accurate. This is why measuring instruments are calibrated based on a known measurement. If the instrument consistently returns the correct value of the known measurement, it is safe for use in finding unknown values.

Precision states how well repeated measurements of something generate the same or similar results. Therefore, the precision of measurements refers to how close together the measurements are when you measure the same thing several times. One way to analyze the precision of measurements would be to determine the range, or difference between the lowest and the highest measured values. In the case of the printer paper measurements, the lowest value was 10.9 inches and the highest value was 11.2 inches. Thus, the measured values deviated from each other by, at most, 0.3 inches. These measurements were reasonably precise because they varied by only a fraction of an inch. However, if the measured values had been 10.9 inches, 11.1 inches, and 11.9 inches, then the measurements would not be very precise because there is a lot of variation from one measurement to another.

The measurements in the paper example are both accurate and precise, but in some cases, measurements are accurate but not precise, or they are precise but not accurate. Let us consider a GPS system that is attempting to locate the position of a restaurant in a city. Think of the restaurant location as existing at the center of a bull’s-eye target. Then think of each GPS attempt to locate the restaurant as a black dot on the bull’s eye.

In Figure 1.21 , you can see that the GPS measurements are spread far apart from each other, but they are all relatively close to the actual location of the restaurant at the center of the target. This indicates a low precision, high accuracy measuring system. However, in Figure 1.22 , the GPS measurements are concentrated quite closely to one another, but they are far away from the target location. This indicates a high precision, low accuracy measuring system. Finally, in Figure 1.23 , the GPS is both precise and accurate, allowing the restaurant to be located.

Uncertainty

The accuracy and precision of a measuring system determine the uncertainty of its measurements. Uncertainty is a way to describe your confidence in your measured value, or the range of values that would be consistent with the data. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 inches plus or minus 0.2 inches or 11.0 ± 0.2 inches. The uncertainty in a measurement, A , is often denoted as δA ("delta A "). The actual value of the object may not be within the range given by the measurement and its uncertainty. In our paper length example above, a new set of measurements might produce a length of 14.0 ± 0.2 inches, with the uncertainty based on the accuracy or our reading or repeated measurements. We would also, however, conclude that either one of our measurement sets is incorrect due to an offset in the measurement process in that set, or our measurement correctly identifies that we are measuring different papers. In the former case, the discrepancy between the measured value and the actual value is called a systematic error.

The factors contributing to uncertainty in a measurement include the following:

• Limitations of the measuring device
• The skill of the person making the measurement
• Irregularities in the object being measured
• Any other factors that affect the outcome (highly dependent on the situation)

In the printer paper example uncertainty could be caused by: the fact that the smallest division on the ruler is 0.1 inches, the person using the ruler has bad eyesight, or uncertainty caused by the paper cutting machine (e.g., one side of the paper is slightly longer than the other.) It is good practice to carefully consider all possible sources of uncertainty in a measurement and reduce or eliminate them.

Percent Uncertainty

One method of expressing uncertainty is as a percent of the measured value. If a measurement, A , is expressed with uncertainty, δ A , the percent uncertainty is

Calculating Percent Uncertainty: A Bag of Apples

A grocery store sells 5-lb bags of apples. You purchase four bags over the course of a month and weigh the apples each time. You obtain the following measurements:

• Week 1 weight: 4.8 lb 4.8 lb
• Week 2 weight: 5.3 lb 5.3 lb
• Week 3 weight: 4.9 lb 4.9 lb
• Week 4 weight: 5.4 lb 5.4 lb

You determine that the expected weight of a 5 lb bag has an uncertainty of ±0.4 lb. What is the percent uncertainty of the bag’s weight?

First, observe that the expected value of the bag’s weight, A A , is 5 lb. The uncertainty in this value, δ A δ A , is 0.4 lb. We can use the following equation to determine the percent uncertainty of the weight

Plug the known values into the equation

We can conclude that the weight of the apple bag is 5 lb ± 8 percent. Consider how this percent uncertainty would change if the bag of apples were half as heavy, but the uncertainty in the weight remained the same. Hint for future calculations: when calculating percent uncertainty, always remember that you must multiply the fraction by 100 percent. If you do not do this, you will have a decimal quantity, not a percent value.

Uncertainty in Calculations

There is an uncertainty in anything calculated from measured quantities. For example, the area of a floor calculated from measurements of its length and width has an uncertainty because the both the length and width have uncertainties. How big is the uncertainty in something you calculate by multiplication or division? If the measurements in the calculation have small uncertainties (a few percent or less), then the method of adding percents can be used. This method says that the percent uncertainty in a quantity calculated by multiplication or division is the sum of the percent uncertainties in the items used to make the calculation. For example, if a floor has a length of 4.00 m and a width of 3.00 m, with uncertainties of 2 percent and 1 percent, respectively, then the area of the floor is 12.0 m 2 and has an uncertainty of 3 percent (expressed as an area this is 0.36 m 2 , which we round to 0.4 m 2 since the area of the floor is given to a tenth of a square meter).

For more information on the accuracy, precision, and uncertainty of measurements based upon the units of measurement, visit this website .

Precision of Measuring Tools and Significant Figures

An important factor in the accuracy and precision of measurements is the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, consider measuring the thickness of a coin. A standard ruler can measure thickness to the nearest millimeter, while a micrometer can measure the thickness to the nearest 0.005 millimeter. The micrometer is a more precise measuring tool because it can measure extremely small differences in thickness. The more precise the measuring tool, the more precise and accurate the measurements can be.

When we express measured values, we can only list as many digits as we initially measured with our measuring tool (such as the rulers shown in Figure 1.24 ). For example, if you use a standard ruler to measure the length of a stick, you may measure it with a decimeter ruler as 3.6 cm. You could not express this value as 3.65 cm because your measuring tool was not precise enough to measure a hundredth of a centimeter. It should be noted that the last digit in a measured value has been estimated in some way by the person performing the measurement. For example, the person measuring the length of a stick with a ruler notices that the stick length seems to be somewhere in between 36 mm and 37 mm. He or she must estimate the value of the last digit. The rule is that the last digit written down in a measurement is the first digit with some uncertainty. For example, the last measured value 36.5 mm has three digits, or three significant figures. The number of significant figures in a measurement indicates the precision of the measuring tool. The more precise a measuring tool is, the greater the number of significant figures it can report.

Special consideration is given to zeros when counting significant figures. For example, the zeros in 0.053 are not significant because they are only placeholders that locate the decimal point. There are two significant figures in 0.053—the 5 and the 3. However, if the zero occurs between other significant figures, the zeros are significant. For example, both zeros in 10.053 are significant, as these zeros were actually measured. Therefore, the 10.053 placeholder has five significant figures. The zeros in 1300 may or may not be significant, depending on the style of writing numbers. They could mean the number is known to the last zero, or the zeros could be placeholders. So 1300 could have two, three, or four significant figures. To avoid this ambiguity, write 1300 in scientific notation as 1.3 × 10 3 . Only significant figures are given in the x factor for a number in scientific notation (in the form x × 10 y x × 10 y ). Therefore, we know that 1 and 3 are the only significant digits in this number. In summary, zeros are significant except when they serve only as placeholders. Table 1.4 provides examples of the number of significant figures in various numbers.

Significant Figures in Calculations

When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value. There are two different rules, one for multiplication and division and another rule for addition and subtraction, as discussed below.

For multiplication and division: The answer should have the same number of significant figures as the starting value with the fewest significant figures. For example, the area of a circle can be calculated from its radius using A = π r 2 A = π r 2 . Let us see how many significant figures the area will have if the radius has only two significant figures, for example, r = 2.0 m. Then, using a calculator that keeps eight significant figures, you would get

But because the radius has only two significant figures, the area calculated is meaningful only to two significant figures or

even though the value of π π is meaningful to at least eight digits.

For addition and subtraction : The answer should have the same number places (e.g. tens place, ones place, tenths place, etc.) as the least-precise starting value. Suppose that you buy 7.56 kg of potatoes in a grocery store as measured with a scale having a precision of 0.01 kg. Then you drop off 6.052 kg of potatoes at your laboratory as measured by a scale with a precision of 0.001 kg. Finally, you go home and add 13.7 kg of potatoes as measured by a bathroom scale with a precision of 0.1 kg. How many kilograms of potatoes do you now have, and how many significant figures are appropriate in the answer? The mass is found by simple addition and subtraction:

The least precise measurement is 13.7 kg. This measurement is expressed to the 0.1 decimal place, so our final answer must also be expressed to the 0.1 decimal place. Thus, the answer should be rounded to the tenths place, giving 15.2 kg. The same is true for non-decimal numbers. For example,

We cannot report the decimal places in the answer because 2 has no decimal places that would be significant. Therefore, we can only report to the ones place.

It is a good idea to keep extra significant figures while calculating, and to round off to the correct number of significant figures only in the final answers. The reason is that small errors from rounding while calculating can sometimes produce significant errors in the final answer. As an example, try calculating 5,098 − ( 5.000 ) × ( 1,010 ) 5,098 − ( 5.000 ) × ( 1,010 ) to obtain a final answer to only two significant figures. Keeping all significant during the calculation gives 48. Rounding to two significant figures in the middle of the calculation changes it to 5,100 – (5 .000) × (1,000) = 100, 5,100 – (5 .000) × (1,000) = 100, which is way off. You would similarly avoid rounding in the middle of the calculation in counting and in doing accounting, where many small numbers need to be added and subtracted accurately to give possibly much larger final numbers.

Remind students that they will be expected to report the proper number of significant figures on assignment and test problems.

Significant Figures in this Text

In this textbook, most numbers are assumed to have three significant figures. Furthermore, consistent numbers of significant figures are used in all worked examples. You will note that an answer given to three digits is based on input good to at least three digits. If the input has fewer significant figures, the answer will also have fewer significant figures. Care is also taken that the number of significant figures is reasonable for the situation posed. In some topics, such as optics, more than three significant figures will be used. Finally, if a number is exact, such as the 2 in the formula, c = 2 π r c = 2 π r , it does not affect the number of significant figures in a calculation.

Approximating Vast Numbers: a Trillion Dollars

The U.S. federal deficit in the 2008 fiscal year was a little greater than $10 trillion. Most of us do not have any concept of how much even one trillion actually is. Suppose that you were given a trillion dollars in $100 bills. If you made 100-bill stacks, like that shown in Figure 1.25 , and used them to evenly cover a football field (between the end zones), make an approximation of how high the money pile would become. (We will use feet/inches rather than meters here because football fields are measured in yards.) One of your friends says 3 in., while another says 10 ft. What do you think?

When you imagine the situation, you probably envision thousands of small stacks of 100 wrapped $100 bills, such as you might see in movies or at a bank. Since this is an easy-to-approximate quantity, let us start there. We can find the volume of a stack of 100 bills, find out how many stacks make up one trillion dollars, and then set this volume equal to the area of the football field multiplied by the unknown height.

• Calculate the volume of a stack of 100 bills. The dimensions of a single bill are approximately 3 in. by 6 in. A stack of 100 of these is about 0.5 in. thick. So the total volume of a stack of 100 bills is volume of stack = length × width × height, volume of stack = 6 in . × 3 in . × 0 .5 in ., volume of stack = 9 in . 3 . volume of stack = length × width × height, volume of stack = 6 in . × 3 in . × 0 .5 in ., volume of stack = 9 in . 3 .

Calculate the number of stacks. Note that a trillion dollars is equal to $ 1 × 10 12 $ 1 × 10 12 , and a stack of one-hundred $ 100 $ 100 bills is equal to $ 10 , 000 , $ 10 , 000 , or $ 1 × 10 4 $ 1 × 10 4 . The number of stacks you will have is

Calculate the area of a football field in square inches. The area of a football field is 100  yd ×  50 yd 100  yd ×  50 yd , which gives 5 , 000  yd 2 5 , 000  yd 2 . Because we are working in inches, we need to convert square yards to square inches

This conversion gives us 6 × 10 6  in . 2 6 × 10 6  in . 2 for the area of the field. (Note that we are using only one significant figure in these calculations.)

• Calculate the total volume of the bills. The volume of all the $100-bill stacks is 9 in . 3  / stack × 10 8  stacks = 9 × 10 8  in . 3 9 in . 3  / stack × 10 8  stacks = 9 × 10 8  in . 3

The height of the money will be about 100 in. high. Converting this value to feet gives

The final approximate value is much higher than the early estimate of 3 in., but the other early estimate of 10 ft (120 in.) was roughly correct. How did the approximation measure up to your first guess? What can this exercise tell you in terms of rough guesstimates versus carefully calculated approximations?

In the example above, the final approximate value is much higher than the first friend’s early estimate of 3 in. However, the other friend’s early estimate of 10 ft. (120 in.) was roughly correct. How did the approximation measure up to your first guess? What can this exercise suggest about the value of rough guesstimates versus carefully calculated approximations?

In [link] , point out to students the importance of precision in their measurements. Greater precision allows measurements to be less uncertain, and therefore, a close approximation rather than a guesstimate.

Graphing in Physics

Most results in science are presented in scientific journal articles using graphs. Graphs present data in a way that is easy to visualize for humans in general, especially someone unfamiliar with what is being studied. They are also useful for presenting large amounts of data or data with complicated trends in an easily-readable way.

One commonly-used graph in physics and other sciences is the line graph , probably because it is the best graph for showing how one quantity changes in response to the other. Let’s build a line graph based on the data in Table 1.5 , which shows the measured distance that a train travels from its station versus time. Our two variables , or things that change along the graph, are time in minutes, and distance from the station, in kilometers. Remember that measured data may not have perfect accuracy.

• Draw the two axes. The horizontal axis, or x -axis, shows the independent variable , which is the variable that is controlled or manipulated. The vertical axis, or y -axis, shows the dependent variable , the non-manipulated variable that changes with (or is dependent on) the value of the independent variable. In the data above, time is the independent variable and should be plotted on the x -axis. Distance from the station is the dependent variable and should be plotted on the y -axis.
• Label each axes on the graph with the name of each variable, followed by the symbol for its units in parentheses. Be sure to leave room so that you can number each axis. In this example, use Time (min) as the label for the x -axis.

Next, you must determine the best scale to use for numbering each axis. Because the time values on the x -axis are taken every 10 minutes, we could easily number the x -axis from 0 to 70 minutes with a tick mark every 10 minutes. Likewise, the y -axis scale should start low enough and continue high enough to include all of the distance from station values. A scale from 0 km to 160 km should suffice, perhaps with a tick mark every 10 km.

In general, you want to pick a scale for both axes that 1) shows all of your data, and 2) makes it easy to identify trends in your data. If you make your scale too large, it will be harder to see how your data change. Likewise, the smaller and more fine you make your scale, the more space you will need to make the graph. The number of significant figures in the axis values should be coarser than the number of significant figures in the measurements.

• Add a title to the top of the graph to state what the graph is describing, such as the y -axis parameter vs. the x -axis parameter. In the graph shown here, the title is train motion . It could also be titled distance of the train from the station vs. time.

[OL] The importance of bar graphs should also be mentioned as a useful way to show data relations when one variable is not continuous, such as in a frequency histogram, which compares how many data points fall into discrete categories.

[OL] If students have difficulty understanding the difference between dependent and independent variables in the train example, explain that time is independent because it will continue to move forward at the same rate whether the train leaves the station or not.

Analyzing a Graph Using Its Equation

One way to get a quick snapshot of a dataset is to look at the equation of its trend line . If the graph produces a straight line, the equation of the trend line takes the form

The b in the equation is the y -intercept while the m in the equation is the slope . The y -intercept tells you at what y value the line intersects the y -axis. In the case of the graph above, the y -intercept occurs at 0, at the very beginning of the graph. The y -intercept, therefore, lets you know immediately where on the y -axis the plot line begins.

The m in the equation is the slope. This value describes how much the line on the graph moves up or down on the y -axis along the line’s length. The slope is found using the following equation

In order to solve this equation, you need to pick two points on the line (preferably far apart on the line so the slope you calculate describes the line accurately). The quantities Y 2 and Y 1 represent the y -values from the two points on the line (not data points) that you picked, while X 2 and X 1 represent the two x -values of the those points.

What can the slope value tell you about the graph? The slope of a perfectly horizontal line will equal zero, while the slope of a perfectly vertical line will be undefined because you cannot divide by zero. A positive slope indicates that the line moves up the y -axis as the x -value increases while a negative slope means that the line moves down the y -axis. The more negative or positive the slope is, the steeper the line moves up or down, respectively. The slope of our graph in Figure 1.26 is calculated below based on the two endpoints of the line

Equation of line: y = ( 2.0  km/min ) x + 0 y = ( 2.0  km/min ) x + 0

Because the x axis is time in minutes, we would actually be more likely to use the time t as the independent ( x- axis) variable and write the equation as

The formula y = m x + b y = m x + b only applies to linear relationships , or ones that produce a straight line. Another common type of line in physics is the quadratic relationship , which occurs when one of the variables is squared. One quadratic relationship in physics is the relation between the speed of an object its centripetal acceleration, which is used to determine the force needed to keep an object moving in a circle. Another common relationship in physics is the inverse relationship , in which one variable decreases whenever the other variable increases. An example in physics is Coulomb’s law. As the distance between two charged objects increases, the electrical force between the two charged objects decreases. Inverse proportionality , such the relation between x and y in the equation

for some number k , is one particular kind of inverse relationship. A third commonly-seen relationship is the exponential relationship , in which a change in the independent variable produces a proportional change in the dependent variable. As the value of the dependent variable gets larger, its rate of growth also increases. For example, bacteria often reproduce at an exponential rate when grown under ideal conditions. As each generation passes, there are more and more bacteria to reproduce. As a result, the growth rate of the bacterial population increases every generation ( Figure 1.28 ).

Using Logarithmic Scales in Graphing

Sometimes a variable can have a very large range of values. This presents a problem when you’re trying to figure out the best scale to use for your graph’s axes. One option is to use a logarithmic (log) scale . In a logarithmic scale, the value each mark labels is the previous mark’s value multiplied by some constant. For a log base 10 scale, each mark labels a value that is 10 times the value of the mark before it. Therefore, a base 10 logarithmic scale would be numbered: 0, 10, 100, 1,000, etc. You can see how the logarithmic scale covers a much larger range of values than the corresponding linear scale, in which the marks would label the values 0, 10, 20, 30, and so on.

If you use a logarithmic scale on one axis of the graph and a linear scale on the other axis, you are using a semi-log plot . The Richter scale, which measures the strength of earthquakes, uses a semi-log plot. The degree of ground movement is plotted on a logarithmic scale against the assigned intensity level of the earthquake, which ranges linearly from 1-10 ( Figure 1.29 (a) ).

If a graph has both axes in a logarithmic scale, then it is referred to as a log-log plot . The relationship between the wavelength and frequency of electromagnetic radiation such as light is usually shown as a log-log plot ( Figure 1.29 (b) ). Log-log plots are also commonly used to describe exponential functions, such as radioactive decay.

Method of Adding Percents: Shingling Your Roof

A series of shingles are used to protect the roof of a home. Using a measuring tape, you measure one shingle and find its dimensions to be 44 cm by 100 cm. Knowing that your measurements are not perfect, you estimate an uncertainty of ±0.5 cm. Following the method of adding percents, what is the area of the shingle, including uncertainty?

While calculating the area of the shingle is straightforward (44 cm x 100 cm = 4400 cm 2 ), determining the percent uncertainty is more challenging. In order to use the method of adding percents, you must first calculate the percent uncertainty of each measurement.

Length % Uncertainty: 𝜹A/A x 100% = 0.5/44 x 100% = 1.1% Width % Uncertainty: 𝜹A/A x 100% = 0.5/100 x 100% = 0.5%

Adding Percents: 1.1% + 0.5% = 1.6% uncertainty

Area of the Shingle: 4400 cm 2 ± 1.6%

Note that this uncertainty can also be expressed in metric terms.

1.6% x 4400 cm 2 = 70.4 cm 2

Area of the Shingle: 4400 ± 70.4 cm 2

Knowing the percent uncertainty of a shingle can help a contractor determine the number of shingles needed, and therefore the cost, of roofing a new home. Consider how using smaller shingles would affect this uncertainty, and what role this would play in the cost estimation process.

Virtual Physics

Graphing lines.

In this simulation you will examine how changing the slope and y -intercept of an equation changes the appearance of a plotted line. Select slope-intercept form and drag the blue circles along the line to change the line’s characteristics. Then, play the line game and see if you can determine the slope or y -intercept of a given line.

Grasp Check

How would the following changes affect a line that is neither horizontal nor vertical and has a positive slope?

• increase the slope but keeping the y -intercept constant
• Increasing the slope will cause the line to rotate clockwise around the y -intercept. Increasing the y -intercept will cause the line to move vertically up on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate counter-clockwise around the y -intercept. Increasing the y -intercept will cause the line to move vertically up on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate clockwise around the y -intercept. Increasing the y -intercept will cause the line to move horizontally right on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate counter-clockwise around the y -intercept. Increasing the y -intercept will cause the line to move horizontally right on the graph without changing the line’s slope.

Check Your Understanding

• Conversion between units is easier in metric units.
• Comparison of physical quantities is easy in metric units.
• Metric units are more modern than English units.
• Metric units are based on powers of 2.
• Precision states how much repeated measurements generate the same or closely similar results, while accuracy states how close a measurement is to the true value of the measurement.
• Precision states how close a measurement is to the true value of the measurement, while accuracy states how much repeated measurements generate the same or closely similar result.
• Precision and accuracy are the same thing. They state how much repeated measurements generate the same or closely similar results.
• Precision and accuracy are the same thing. They state how close a measurement is to the true value of the measurement.

Use the Check Your Understanding questions to assess students’ achievement of the sections learning objectives. If students are struggling with a specific objective, the Check Your Understanding will help identify which and direct students to the relevant content.

• 1 See Appendix A for a discussion of powers of 10.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: Physics
• Publication date: Mar 26, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/physics/pages/1-introduction
• Section URL: https://openstax.org/books/physics/pages/1-3-the-language-of-physics-physical-quantities-and-units

© Jun 7, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

The Nature of Science and Physics

Physical quantities and units, learning objectives.

By the end of this section, you will be able to:

• Perform unit conversions both in the SI and English units.
• Explain the most common prefixes in the SI units and be able to write them in scientific notation.

Figure 1. The distance from Earth to the Moon may seem immense, but it is just a tiny fraction of the distances from Earth to other celestial bodies. (credit: NASA)

We define a physical quantity either by specifying how it is measured or by stating how it is calculated from other measurements. For example, we define distance and time by specifying methods for measuring them, whereas we define average speed by stating that it is calculated as distance traveled divided by time of travel.

Measurements of physical quantities are expressed in terms of units , which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in units of meters (for sprinters) or kilometers (for distance runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way. (See Figure 2.)

Figure 2. Distances given in unknown units are maddeningly useless.

There are two major systems of units used in the world: SI units (also known as the metric system) and English units (also known as the customary or imperial system). English units were historically used in nations once ruled by the British Empire and are still widely used in the United States. Virtually every other country in the world now uses SI units as the standard; the metric system is also the standard system agreed upon by scientists and mathematicians. The acronym “SI” is derived from the French Système International .

SI Units: Fundamental and Derived Units

Table 1 gives the fundamental SI units that are used throughout this textbook. This text uses non-SI units in a few applications where they are in very common use, such as the measurement of blood pressure in millimeters of mercury (mm Hg). Whenever non-SI units are discussed, they will be tied to SI units through conversions.

It is an intriguing fact that some physical quantities are more fundamental than others and that the most fundamental physical quantities can be defined only in terms of the procedure used to measure them. The units in which they are measured are thus called fundamental units . In this textbook, the fundamental physical quantities are taken to be length, mass, time, and electric current. (Note that electric current will not be introduced until much later in this text.) All other physical quantities, such as force and electric charge, can be expressed as algebraic combinations of length, mass, time, and current (for example, speed is length divided by time); these units are called derived units .

Units of Time, Length, and Mass: The Second, Meter, and Kilogram

The SI unit for time, the second (abbreviated s), has a long history. For many years it was defined as 1/86,400 of a mean solar day. More recently, a new standard was adopted to gain greater accuracy and to define the second in terms of a non-varying, or constant, physical phenomenon (because the solar day is getting longer due to very gradual slowing of the Earth’s rotation). Cesium atoms can be made to vibrate in a very steady way, and these vibrations can be readily observed and counted. In 1967 the second was redefined as the time required for 9,192,631,770 of these vibrations. (See Figure 3.) Accuracy in the fundamental units is essential, because all measurements are ultimately expressed in terms of fundamental units and can be no more accurate than are the fundamental units themselves.

Figure 3. An atomic clock such as this one uses the vibrations of cesium atoms to keep time to a precision of better than a microsecond per year. The fundamental unit of time, the second, is based on such clocks. This image is looking down from the top of an atomic fountain nearly 30 feet tall! (credit: Steve Jurvetson/Flickr)

The SI unit for length is the meter (abbreviated m); its definition has also changed over time to become more accurate and precise. The meter was first defined in 1791 as 1/10,000,000 of the distance from the equator to the North Pole. This measurement was improved in 1889 by redefining the meter to be the distance between two engraved lines on a platinum-iridium bar now kept near Paris. By 1960, it had become possible to define the meter even more accurately in terms of the wavelength of light, so it was again redefined as 1,650,763.73 wavelengths of orange light emitted by krypton atoms. In 1983, the meter was given its present definition (partly for greater accuracy) as the distance light travels in a vacuum in 1/299,792,458 of a second. (See Figure 4.) This change defines the speed of light to be exactly 299,792,458 meters per second. The length of the meter will change if the speed of light is someday measured with greater accuracy.

The Kilogram

The SI unit for mass is the kilogram (abbreviated kg); it is defined to be the mass of a platinum-iridium cylinder kept with the old meter standard at the International Bureau of Weights and Measures near Paris. Exact replicas of the standard kilogram are also kept at the United States’ National Institute of Standards and Technology, or NIST, located in Gaithersburg, Maryland outside of Washington D.C., and at other locations around the world. The determination of all other masses can be ultimately traced to a comparison with the standard mass.

Figure 4. The meter is defined to be the distance light travels in 1/299,792,458 of a second in a vacuum. Distance traveled is speed multiplied by time.

Electric current and its accompanying unit, the ampere, will be introduced in Introduction to Electric Current, Resistance, and Ohm’s Law when electricity and magnetism are covered. The initial modules in this textbook are concerned with mechanics, fluids, heat, and waves. In these subjects all pertinent physical quantities can be expressed in terms of the fundamental units of length, mass, and time.

Metric Prefixes

SI units are part of the metric system . The metric system is convenient for scientific and engineering calculations because the units are categorized by factors of 10. Table 2 gives metric prefixes and symbols used to denote various factors of 10.

Metric systems have the advantage that conversions of units involve only powers of 10. There are 100 centimeters in a meter, 1000 meters in a kilometer, and so on. In non-metric systems, such as the system of U.S. customary units, the relationships are not as simple—there are 12 inches in a foot, 5280 feet in a mile, and so on. Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by using an appropriate metric prefix. For example, distances in meters are suitable in construction, while distances in kilometers are appropriate for air travel, and the tiny measure of nanometers are convenient in optical design. With the metric system there is no need to invent new units for particular applications.

The term order of magnitude refers to the scale of a value expressed in the metric system. Each power of 10 in the metric system represents a different order of magnitude. For example, 10 1 , 10 2 , 10 3 , and so forth are all different orders of magnitude. All quantities that can be expressed as a product of a specific power of 10 are said to be of the same order of magnitude. For example, the number 800 can be written as 8 × 10 2 , and the number 450 can be written as 4.5 × 10 2 . Thus, the numbers 800 and 450 are of the same order of magnitude: 10 2 . Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of 10 -9 m while the diameter of the Sun is on the order of 10 9 m.

The Quest for Microscopic Standards for Basic Units

The fundamental units described in this chapter are those that produce the greatest accuracy and precision in measurement. There is a sense among physicists that, because there is an underlying microscopic substructure to matter, it would be most satisfying to base our standards of measurement on microscopic objects and fundamental physical phenomena such as the speed of light. A microscopic standard has been accomplished for the standard of time, which is based on the oscillations of the cesium atom.

The standard for length was once based on the wavelength of light (a small-scale length) emitted by a certain type of atom, but it has been supplanted by the more precise measurement of the speed of light. If it becomes possible to measure the mass of atoms or a particular arrangement of atoms such as a silicon sphere to greater precision than the kilogram standard, it may become possible to base mass measurements on the small scale. There are also possibilities that electrical phenomena on the small scale may someday allow us to base a unit of charge on the charge of electrons and protons, but at present current and charge are related to large-scale currents and forces between wires.

Known Ranges of Length, Mass, and Time

The vastness of the universe and the breadth over which physics applies are illustrated by the wide range of examples of known lengths, masses, and times in Table 1.3. Examination of this table will give you some feeling for the range of possible topics and numerical values. (See Figure 5 and Figure 6.)

Figure 5. Tiny phytoplankton swims among crystals of ice in the Antarctic Sea. They range from a few micrometers to as much as 2 millimeters in length. (credit: Prof. Gordon T. Taylor, Stony Brook University; NOAA Corps Collections)

Figure 6. Galaxies collide 2.4 billion light years away from Earth. The tremendous range of observable phenomena in nature challenges the imagination. (credit: NASA/CXC/UVic./A. Mahdavi et al. Optical/lensing: CFHT/UVic./H. Hoekstra et al.)

Unit Conversion and Dimensional Analysis

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook, some quantities may be expressed in units of liters and you need to convert them to cups. Or, perhaps you are reading walking directions from one location to another and you are interested in how many miles you will be walking. In this case, you will need to convert units of feet to miles.

Let us consider a simple example of how to convert units. Let us say that we want to convert 80 meters (m) to kilometers (km).

The first thing to do is to list the units that you have and the units that you want to convert to. In this case, we have units in meters and we want to convert to kilometers .

Next, we need to determine a conversion factor relating meters to kilometers. A conversion factor is a ratio expressing how many of one unit are equal to another unit. For example, there are 12 inches in 1 foot, 100 centimeters in 1 meter, 60 seconds in 1 minute, and so on. In this case, we know that there are 1,000 meters in 1 kilometer.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor so that the units cancel out, as shown:

[latex]80\overline{)\text{m}}\times \frac{\text{1 km}}{1000\overline{)\text{m}}}=0\text{.080 km.}[/latex]

Note that the unwanted m unit cancels, leaving only the desired km unit. You can use this method to convert between any types of unit.

Example 1.  Unit Conversions – A Short Drive Home

Suppose that you drive the 10.0 km from your university to home in 20.0 min. Calculate your average speed (a) in kilometers per hour (km/h) and (b) in meters per second (m/s). (Note: Average speed is distance traveled divided by time of travel.)

First we calculate the average speed using the given units. Then we can get the average speed into the desired units by picking the correct conversion factor and multiplying by it. The correct conversion factor is the one that cancels the unwanted unit and leaves the desired unit in its place.

Solution for (a)

(1) Calculate average speed. Average speed is distance traveled divided by time of travel. (Take this definition as a given for now—average speed and other motion concepts will be covered in a later module.) In equation form,

(2) Substitute the given values for distance and time.

(3) Convert km/min to km/h: multiply by the conversion factor that will cancel minutes and leave hours. That conversion factor is 60 min/hr. Thus,

Discussion for (a)

To check your answer, consider the following:

(1) Be sure that you have properly cancelled the units in the unit conversion. If you have written the unit conversion factor upside down, the units will not cancel properly in the equation. If you accidentally get the ratio upside down, then the units will not cancel; rather, they will give you the wrong units as follows:

which are obviously not the desired units of km/h.

(2) Check that the units of the final answer are the desired units. The problem asked us to solve for average speed in units of km/h and we have indeed obtained these units.

(3) Check the significant figures. Because each of the values given in the problem has three significant figures, the answer should also have three significant figures. The answer 30.0 km/hr does indeed have three significant figures, so this is appropriate. Note that the significant figures in the conversion factor are not relevant because an hour is defined to be 60 minutes, so the precision of the conversion factor is perfect.

(4) Next, check whether the answer is reasonable. Let us consider some information from the problem—if you travel 10 km in a third of an hour (20 min), you would travel three times that far in an hour. The answer does seem reasonable.

Solution for (b)

There are several ways to convert the average speed into meters per second.

(1) Start with the answer to (a) and convert km/h to m/s. Two conversion factors are needed—one to convert hours to seconds, and another to convert kilometers to meters.

(2) Multiplying by these yields

Discussion for (b)

If we had started with 0.500 km/min, we would have needed different conversion factors, but the answer would have been the same: 8.33 m/s.

You may have noted that the answers in the worked example just covered were given to three digits. Why? When do you need to be concerned about the number of digits in something you calculate? Why not write down all the digits your calculator produces? The module Accuracy, Precision, and Significant Figures will help you answer these questions.

Nonstandard Units

While there are numerous types of units that we are all familiar with, there are others that are much more obscure. For example, a firkin is a unit of volume that was once used to measure beer. One firkin equals about 34 liters. To learn more about nonstandard units, use a dictionary or encyclopedia to research different “weights and measures.” Take note of any unusual units, such as a barleycorn, that are not listed in the text. Think about how the unit is defined and state its relationship to SI units.

Check Your Understanding

1. Some hummingbirds beat their wings more than 50 times per second. A scientist is measuring the time it takes for a hummingbird to beat its wings once. Which fundamental unit should the scientist use to describe the measurement? Which factor of 10 is the scientist likely to use to describe the motion precisely? Identify the metric prefix that corresponds to this factor of 10.

2. One cubic centimeter is equal to one milliliter. What does this tell you about the different units in the SI metric system?

1. The scientist will measure the time between each movement using the fundamental unit of seconds. Because the wings beat so fast, the scientist will probably need to measure in milliseconds, or 10 -3 seconds. (50 beats per second corresponds to 20 milliseconds per beat.)

2. The fundamental unit of length (meter) is probably used to create the derived unit of volume (liter). The measure of a milliliter is dependent on the measure of a centimeter.

Section Summary

• Physical quantities are a characteristic or property of an object that can be measured or calculated from other measurements.
• Units are standards for expressing and comparing the measurement of physical quantities. All units can be expressed as combinations of four fundamental units.
• The four fundamental units we will use in this text are the meter (for length), the kilogram (for mass), the second (for time), and the ampere (for electric current). These units are part of the metric system, which uses powers of 10 to relate quantities over the vast ranges encountered in nature.
• The four fundamental units are abbreviated as follows: meter, m; kilogram, kg; second, s; and ampere, A. The metric system also uses a standard set of prefixes to denote each order of magnitude greater than or lesser than the fundamental unit itself.
• Unit conversions involve changing a value expressed in one type of unit to another type of unit. This is done by using conversion factors, which are ratios relating equal quantities of different units.

Conceptual Questions

1. Identify some advantages of metric units.

Problems & Exercises

1. The speed limit on some interstate highways is roughly 100 km/h. (a) What is this in meters per second? (b) How many miles per hour is this?

2. A car is traveling at a speed of 33 m/s. (a) What is its speed in kilometers per hour? (b) Is it exceeding the 90 km/h speed limit?

3. Show that 1.0 m/s = 3.6 km/h. Hint: Show the explicit steps involved in converting 1.0 m/s = 3.6 km/h.

4. American football is played on a 100-yd-long field, excluding the end zones. How long is the field in meters? (Assume that 1 meter equals 3.281 feet.)

5. Soccer fields vary in size. A large soccer field is 115 m long and 85 m wide. What are its dimensions in feet and inches? (Assume that 1 meter equals 3.281 feet.)

6. What is the height in meters of a person who is 6 ft 1.0 in. tall? (Assume that 1 meter equals 39.37 in.)

7. Mount Everest, at 29,028 feet, is the tallest mountain on the Earth. What is its height in kilometers? (Assume that 1 kilometer equals 3,281 feet.)

8. The speed of sound is measured to be 342 m/s on a certain day. What is this in km/h?

9. Tectonic plates are large segments of the Earth’s crust that move slowly. Suppose that one such plate has an average speed of 4.0 cm/year. (a) What distance does it move in 1 s at this speed? (b) What is its speed in kilometers per million years?

10. (a) Refer to Table 2: Metric Prefixes for Powers of 10 and their Symbols  to determine the average distance between the Earth and the Sun. Then calculate the average speed of the Earth in its orbit in kilometers per second. (b) What is this in meters per second?

Selected Solutions to Problems & Exercises

1. (a) 27.8 m/s (b) 62.1 mph

3. [latex]\frac{\text{1.0 m}}{s}=\frac{1\text{.}\text{0 m}}{s}\times \frac{\text{3600 s}}{\text{1 hr}}\times \frac{1 km}{\text{1000 m}}[/latex]

5. length: 377 ft ; 4 . 53  ×  10 3  in . width: 280 ft ; 3 . 3  ×  10 3  in .

7. 8.847 kn

9. (a) 1 . 3  ×  10 − 9  m  (b) 40 km/My

• See Appendix A for a discussion of powers of 10. ↵
• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

P-1. Physical Quantities, Units, and Measurements

Physics Department of Douglas College; OpenStax; and Joey Wu

• Understand the definitions of quantity, fundamental quantity, and derived quantity.
• Explain the most common prefixes in the SI units and be able to write them in scientific notation

The world around us is full of things we can measure, from very small to very large. Think about the size of a grain of sand compared to the height of a tall building, or the weight of a feather compared to the weight of an elephant. To understand and describe these different sizes and amounts, we use numbers and units.

When we talk about a physical quantity , we’re referring to something we can measure or calculate . For example, we can measure how tall someone is or how long it takes to run across a playground. We can also calculate things like how fast someone is running by using other measurements we’ve made. Every measurement provides three kinds of information:

• the size or magnitude of the measurement (a number),
• a standard of comparison for the measurement (a unit), and
• an indication of the uncertainty of the measurement.

While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.

The number in the measurement can be represented in different ways, including decimal form and scientific notation. (Scientific notation is also known as exponential notation.) For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as 2.98 x 10 5  kg. The mass of the average mosquito is about 0.0000025 kilograms, which can be written as 2.5 x 10 −6  kg.

When we measure the physical quantities, we use units . Units are agreed-upon standard amounts that everyone understands . For instance, we might measure someone’s height in centimeters or inches, or measure the length of a football field in meters or yards. Using these standard units helps everyone understand and compare measurements.

Without units, a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire: 100 mg given three times per day can be effective as an anticonvulsant, but a single dose of 100 g is more than 10 times the lethal amount.

The system of units called the metric system . The most common units in this system are meters for length , kilograms for mass (which is similar to weight), and seconds for time . By using these standard units, scientists (and students!) all over the world can share and understand each other’s measurements.

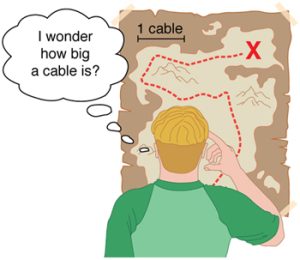
In the world of measurement, there are two main systems of units that people use: the metric system and the customary system . The metric system, also called SI units (which stands for International System of Units in English; the acronym “SI” is derived from the French Système International ), is used by most countries around the world and by scientists everywhere. It includes units like meters, grams, and liters. The customary system, sometimes called English units or imperial units, is mainly used in the United States for everyday measurements. This system includes units like inches, pounds, and cups.

In our science classes, we’ll focus on the metric system because it’s what scientists use and it’s easier to work with. The metric system uses units that are all related by factors of 10, which makes converting between them simpler. For example, there are 100 centimeters in a meter, and 1000 meters in a kilometer. This consistency makes the metric system very useful for scientific measurements and calculations.

Here’s an interesting story that shows why using the same measurement system is so important:

In 1999, NASA (the US space agency) sent a spacecraft called the Mars Climate Orbiter to study Mars. It was supposed to orbit around Mars and send back information about the planet’s weather. But something went wrong, and the spacecraft crashed into Mars instead of orbiting it!

What happened? It turned out that two teams working on the project were using different measurement systems. One team was using metric units (like meters and kilometers), while the other was using customary units (like feet and miles). This meant that when they shared information, they were misunderstanding each other’s numbers.

Because of this mix-up, the spacecraft got too close to Mars and burned up in its atmosphere. This mistake cost $125 million!

This story shows us why it’s so important for scientists to agree on which measurement system to use. It also reminds us to always check our units when we’re doing math and science!

If you’re interested in the story, click https://sma.nasa.gov/docs/default-source/safety-messages/safetymessage-2009-08-01-themarsclimateorbitermishap.pdf?sfvrsn=eaa1ef8_4

SI Units: Fundamental and Derived Units

The metric system, which we use in science, is managed by an international organization in France. This organization makes sure that everyone around the world agrees on how to define and use metric units. Table 1.1 below shows the seven basic metric units. These are called the fundamental units because they’re the building blocks for measuring many things in science:

In this course, we will mainly focus on three basic metric units: Length (meter), Mass (Kilogram), and Time (Seconds) .

These fundamental units are special because we define them based on how we measure them. For example, we define a meter as the distance light travels in a tiny fraction of a second. There are seven fundamental units in the metric system. In this course, we will mainly focus on three of them, as listed in Table 1.

Sometimes, we need to measure other things that aren’t directly covered by these fundamental units. For instance, when we want to measure how fast something is moving (speed), we use a combination of length (meters) and time (seconds). We call these combinations “ derived units ” because they come from our fundamental units.

Remember, using these standard units helps everyone in science speak the same “language” when it comes to measurements. This way, scientists (and students!) from different parts of the world can easily understand and use each other’s work.

Units of Time, Length, and Mass: The Second, Meter, and Kilogram

The second is our unit for measuring time. It’s the time it takes for something very tiny (an atom) to vibrate 9,192,631,770 times! Scientists chose this definition because it’s very precise and doesn’t change. Before this, people used to define a second based on how long it takes the Earth to spin around once, but that wasn’t as accurate because the Earth’s rotation is actually slowing down very gradually.  

The meter is our unit for measuring length. Today, we define a meter as the distance light travels in about 1/300,000,000 of a second. That’s super fast! Scientists chose this definition because the speed of light is always the same, so it gives us a very accurate way to measure distance.

Fun fact: Before this, people tried defining the meter in different ways. They once said it was one ten-millionth of the distance from the North Pole to the equator. Later, they made a special metal bar and said the meter was the length between two lines on that bar. But using light is much more precise!

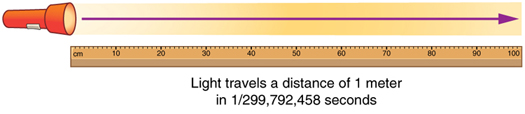
The Kilogram

The kilogram is our unit for measuring mass . For a long time, the kilogram was defined by a special metal cylinder kept in France. All other weights in the world were based on this one cylinder! In 2019, scientists redefined the kilogram using a fundamental constant of nature called the Planck constant. This constant relates a particle’s energy to its frequency, and it’s always the same everywhere in the universe.

The new definition involves a special device called the Kibble balance, which uses electromagnetic forces to balance the weight of a mass. By relating this balance to the Planck constant, scientists can now define the kilogram without relying on a physical object. This new definition is more stable and precise than the old method of using a physical cylinder. It ensures that the kilogram will remain constant over time and can be reproduced anywhere in the world using the right equipment.

While the details of this process are complex, the important thing for us to understand is that scientists are always working to make our measurements more accurate and reliable. This new definition of the kilogram is a great example of how science is always improving and refining our understanding of the world.

Why are these definitions so important? Scientists need very precise measurements to do their work. By defining our basic units (second, meter, and kilogram) in these accurate ways, we make sure that everyone around the world is measuring things in exactly the same way. This helps scientists work together and trust each other’s results, no matter where they are in the world.

In our course, we’ll use these units to measure all sorts of things related to motion, force, and energy. Everything we measure will be based on combinations of length, mass, and time!

The Metric System: A Simple Way to Measure Big and Small Things

SI units are part of the metric system . The metric system is convenient for scientific and engineering calculations because the units are categorized by factors of 10. The table below gives metric prefixes and symbols used to denote various factors of 10.

The metric system, which includes our SI units, is great for science because it uses a simple pattern based on the number 10. This makes it easy to convert between different sizes of units.

Here’s why the metric system is so handy:

• There are 100 centimeters in a meter
• There are 1000 meters in a kilometer. This is much simpler than the customary system used in the U.S., where there are 12 inches in a foot and 5280 feet in a mile!
• “Kilo-” means 1000 times bigger (like in kilometer)
• “Centi-” means 100 times smaller (like in centimeter)
• “Milli-” means 1000 times smaller (like in millimeter)

When we’re dealing with very big or very small numbers in science, we often use something called “ order of magnitude .” It is defined as the scale of a value expressed in the metric system. This is a way to describe how big or small something is using powers of 10. It’s like a quick way to estimate size.

Here’s how it works: Each time you multiply by 10, you go up one order of magnitude; Each time you divide by 10, you go down one order of magnitude. For example, 10 is one order magnitude bigger than 1, 100 is two orders of magnitude bigger than 1, 1000 is three orders of magnitude bigger than 1. This is really useful when we’re comparing things that are very different in size. For instance:

• The width of an atom is about 0.0000000001 meters (10^-10 meters)
• The width of a human hair is about 0.0001 meters (10^-4 meters)
• The height of a person is about 1 meter (10^0 meters)
• The diameter of the Earth is about 10,000,000 meters (10^7 meters)

Using orders of magnitude, we can say the Earth is about 17 orders of magnitude wider than an atom! This helps us understand just how much bigger the Earth is compared to an atom.

In your classroom, you can use this concept to help students grasp the vast differences in size between things they study in science, from tiny atoms to huge planets. It’s a great way to build their understanding of scale and proportion, which are important skills in science and math.

Known Ranges of Length, Mass, and Time

The vastness of the universe and the breadth over which physics applies are illustrated by the wide range of examples of known lengths, masses, and times show in the table above.   Examination of this table will give you some feeling for the range of possible topics and numerical values.

Unit Conversion

Sometimes, we need to change from one unit to another. This is called unit conversion, and it’s an important skill in science and everyday life. In many real-world scenarios, we might need to convert recipes from metric to customary units, or understand distances in different units when reading maps or travel information. Unit conversion also reinforces multiplication, division, and working with fractions, thus helping us build mathematical skills.

Let us consider a simple example of how to convert units. Let us say that we want to convert 80 meters (m) to kilometers (km).

The first thing to do is to list the units that you have and the units that you want to convert to. In this case, we have units in meters and we want to convert to kilometers .

Next, we need to determine a conversion factor relating meters to kilometers. A conversion factor is a ratio expressing how many of one unit are equal to another unit. For example, there are 12 inches in 1 foot, 100 centimeters in 1 meter, 60 seconds in 1 minute, and so on. In this case, we know that there are 1,000 meters in 1 kilometer.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor so that the units cancel out, as shown:

Note that the unwanted m unit cancels, leaving only the desired km unit. You can use this method to convert between any types of unit.

Click here to go the Back Matter Appendices.    Appendix  Useful Information for a more complete list of conversion factors.

NONSTANDARD UNITS

While there are numerous types of units that we are all familiar with, there are others that are much more obscure. For example, a firkin is a unit of volume that was once used to measure beer. One firkin equals about 34 liters. To learn more about nonstandard units, use a dictionary or encyclopedia to research different “weights and measures.” Take note of any unusual units, such as a barleycorn, that are not listed in the text. Think about how the unit is defined and state its relationship to SI units.

• Physical quantities are a characteristic or property of an object that can be measured or calculated from other measurements.
• Units are standards for expressing and comparing the measurement of physical quantities. All units can be expressed as combinations of fundamental units.
• The four fundamental units we will use in this text are the meter (for length), the kilogram (for mass), the second (for time), and the ampere (for electric current). These units are part of the metric system, which uses powers of 10 to relate quantities over the vast ranges encountered in nature.
• The three fundamental units are abbreviated as follows: meter, m; kilogram, kg; second, s. The metric system also uses a standard set of prefixes to denote each order of magnitude greater than or lesser than the fundamental unit itself.
• Unit conversions involve changing a value expressed in one type of unit to another type of unit. This is done by using conversion factors, which are ratios relating equal quantities of different units.

Conceptual Questions

1: Identify some advantages of metric units.

Problems & Exercises

1:  The speed limit on some interstate highways is roughly 100 km/h. (a) What is this in meters per second? (b) How many miles per hour is this?

2: American football is played on a 100-yd-long field, excluding the end zones. How long is the field in meters? (Assume that 1 meter equals 1.094 yard)

3: What is the height in meters of a person who is 6 ft 1.0 in. tall? (Assume that 1 meter equals 39.37 in.)

4 : Which of the following are fundamental units, which are derived units?

1: (a) 27.8 m/s   b) 62.1 miles per hour or mph

4: Fundamental units: meter, second

Derived quantity: Joule, meter per second, g/cm 3 , Newton, cm 2 , m 3

Media Attributions

• Mars Climate Orbiter

P-1. Physical Quantities, Units, and Measurements Copyright © 2022 by Physics Department of Douglas College; OpenStax; and Joey Wu is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

CIE AS & A Level Physics 9702: Topic 1: Physical quantities and units- Unit : 1.2 SI units Study Notes

A Level Physics A Level Maths A Level Chemistry A Level Biology

• SI Units – International System of Units

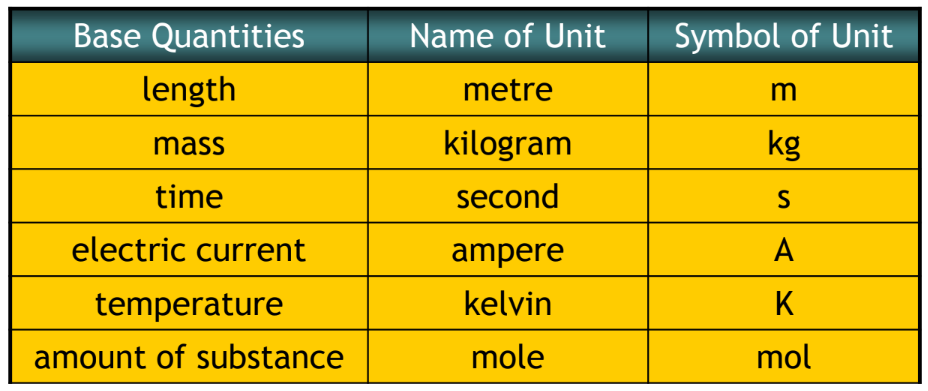
                                                                      Derived quantity & equations

• A derived quantity has an equation which links to other quantities.
• It enables us to express a derived unit in terms of base-unit equivalent.

Example: $\mathrm{F}=\mathrm{ma} ;$ Newton $=\mathrm{kg} \mathrm{m} \mathrm{s}{ }^{-2}$ $ \mathrm{P}=\mathrm{F} / \mathrm{A} ; \quad \text { Pascal }=\mathrm{kg} \mathrm{m} \mathrm{s} \mathrm{m}^{-2} / \mathrm{m}^2=\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2} $

                                                                                Some derived units

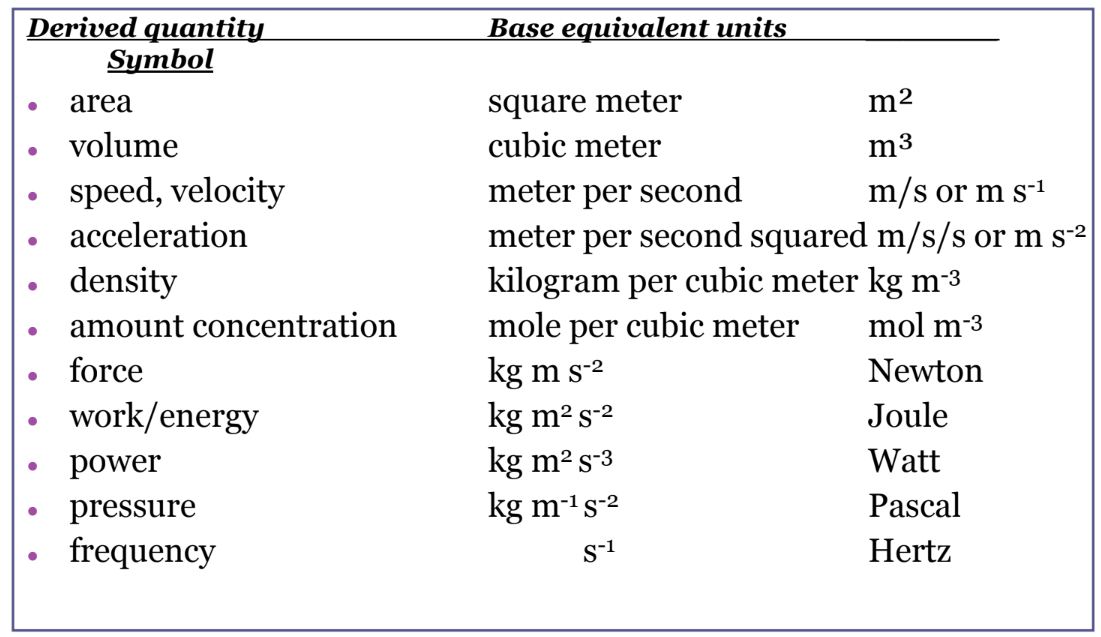
1. Equation: area $=$ length $\times$ width In terms of base units: Units of area $=\mathrm{m} \times \mathrm{m}=\mathrm{m}^2$ 2. Equation: volume $=$ length $\times$ width $\times$ height In terms of base units: Units of volume $=\mathrm{m} \times \mathrm{m} \times \mathrm{m}=\mathrm{m}^3$ 3. Equation: density $=$ mass $\div$ volume In terms of base units: Units of density $=\mathrm{kg} \mathrm{m}^{-3}$

• Work out the derived quantities for:

1. Equation: $\quad$ speed $=\frac{\text { distance }}{\text { time }}$ In terms of base units: Units of speed $=\mathrm{ms}^{-1}$ 2. Equation: $\quad$ acceleration $=\frac{\text { velocity }}{\text { time }}$ In terms of base units: Units of acceleration $=\mathrm{ms}^{-2}$ 3. Equation: force $=$ mass $\times$ acceleration In terms of base units: Units of force $=\mathrm{kg} \mathrm{ms}^{-2}$

1. Equation: $\quad$ Pressure $=\frac{\text { Force }}{\text { Area }}$ In terms of base units: Units of pressure $=\mathrm{Kgm}^{-1} \mathrm{~s}^{-2}$ 2. Equation: Work $=$ Force $\times$ Displacement In terms of base units: Units of work $=\mathrm{Kgm}^2 \mathrm{~S}^{-2}$ 3. Equation: Power $=\frac{\text { Workdone }}{\text { Time }}$ In terms of units: Units of power $=\quad \mathrm{Kgm}^2 \mathrm{~s}^{-3}$

SI Units – Fill in…

For you to know…

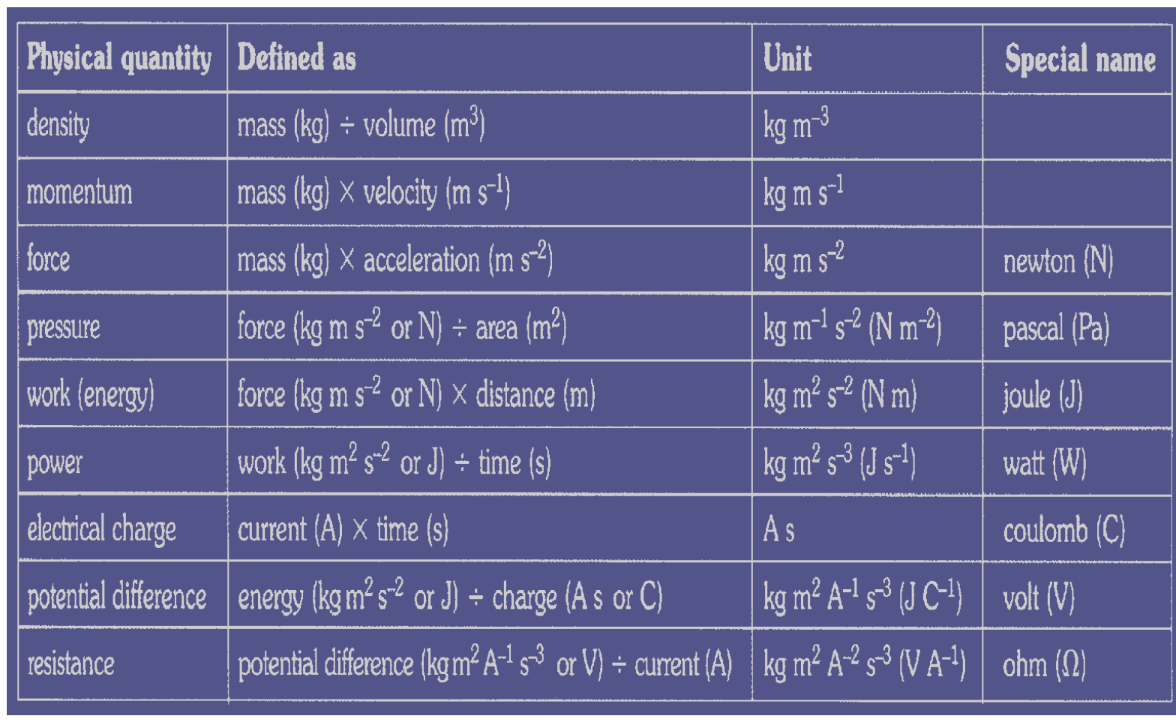
Key Concept

1. A physical quantity is a quantity that can be measured and consists of a numerical magnitude and a unit. 2. The physical quantities can be classified into base quantities and derived quantities. 3. There are seven base quantities: length, mass, time, current, temperature, amount of substance and luminous intensity. 4. The SI units for length, mass, time, temperature and amount of substance, electric current are metre, kilogram, second, kelvin, mole and ampere respectively.

Homogeneity of an equation

• An equation is homogeneous if quantities on BOTH sides of the equation has the same unit.
•  E.g. $s=u t+1 / 2 a^2$
• LHS : unit of $s=m$
• RHS : unit of ut $=\mathbf{m s}^{-1} \mathrm{xS}_{\mathrm{x}}=\mathbf{m}$
•  Unit on LHS = unit on RHS
• Hence equation is homogeneous

Non-homogeneous

• $\mathrm{P}=\rho g h^2$
•  LHS ; unit of $\mathrm{P}=\mathrm{Nm}^{-2}=\mathrm{kgm}^{-1} \mathrm{~s}^{-2}$
•  RHS : unit of $\rho \mathrm{gh}^2=\mathrm{kgm}^{-3}\left(\mathrm{~ms}^{-2}\right)\left(\mathrm{m}^2\right)=\mathrm{kgs}^{-2}$
•  Unit on LHS $\neq$ unit on RHS
• Hence equation is not homogeneous
•  Note: numbers has no unit
•  some constants have no unit.
• A homogeneous eqn may not be physically correct but a physically correct eqn is definitely homogeneous
• E.g. $s=2 u t+a t^2$ (homogenous but not correct)
•  $\quad \mathbf{F}=\mathbf{m a} \quad$ (homogeneous and correct)
• Prefix : magnitudes of physical quantity range from very large to very small.
•  E.g. mass of sun is $10^{30} \mathrm{~kg}$ and mass of electron is $10^{-31} \mathbf{k g}$.
• Hence, prefix is used to describe these magnitudes.

Significant number

•  Magnitudes of physical quantities are often quoted in terms of significant number.
•  Can you tell how many sig. fig. in these numbers?
•  103, 100.0, 0.030, 0.4004, 200
•  If you multiply 2.3 and 1.45, how many sf should you quote?
•  3.19, 3.335, 3.48
•  3.312, 3.335, $3 \cdot 358$

What is Physical Quantity | Types, Example

• Updated by Scienly
• On May 13, 2024

A physical quantity in physics is a quantity which can be defined and measured. For example, mass, length, volume of an object, speed of moving car, distance, force, time, current, etc. are the examples of physical quantities. We describe the laws of physics in the terms of these physical quantities.

Types of Physical Quantity in Physics

There are two types of physical quantities in physics. They are:

• Fundamental quantities
• Derived quantities

Fundamental quantities are those physical quantities that do not depend on any other physical quantity for their measurement. Mass, length, time, electric current, luminous intensity, temperature, and amount of substance are the examples of base or fundamental physical quantities in physics.

In addition to these seven fundamental physical quantities, there are two more physical quantities known as supplementary quantities. These quantities are solid angle and plane angle.

Derived quantities are those physical quantities that are derived from the fundamental physical quantities. In other words, a physical quantity which is derived or obtained by multiplying or dividing one base physical quantity with another base physical quantity is called derived quantity.

For example, area, volume, density, force, velocity, acceleration, linear momentum, etc. All the physical quantities other than seven fundamental or base quantities are derived quantities in physics.

Measurement of Physical Quantities and their Units

Measurement is a process of comparing of an unknown physical quantity with a known standard quantity (or constant quantity). In order to measure any physical quantity, we need two things. They are:

• The unit in which the physical quantity will measure.
• The numerical value which expresses how many times a standard quantity or unit is contained in a given physical quantity.

So, any physical quantity has two components: magnitude (n) of the physical quantity and its unit (u). The number of times a standard unit or quantity is present in a given physical quantity is called magnitude of physical quantity. Thus,

Magnitude of physical quantity = numerical value of physical quantity * size of its unit

Let us suppose that n is the numerical value of a physical quantity, and u is its unit, magnitude Q of physical quantity is Q = nu.

For example, a light travels in air at the speed of 300000 km/s. It means that the magnitude of physical quantity of “speed of light” is 300000 and its unit is km/s.

Let’s take another simple example. If we measure the length of a rod, we will use a metre-scale as a standard. On measurement, if we find that the length is 5 times the standard metre scale, the length is 5 metres. In this statement, 5 is the magnitude of the length and metre is the unit of physical quantity. Thus, if the length of the rod is 3 m, then Q = 3 m where n = 3, u = 1 m.

Remember that there is no meaning of any physical quantity without a proper unit. For example, the radii of two solid spheres are 2 and 6. Then, we cannot sure that which of the two solid spheres are bigger in size? Therefore, it is difficult to estimate the size of anything without a proper unit.

Scalar Quantity and Vector Quantity

A physical quantity which is described completely by its magnitude only is called a scalar quantity. For example, distance, mass, time, speed, density, etc. All these quantities are scalar quantities and are added them according to ordinary algebraic rules.

A physical quantity which is described completely by both their magnitude and direction is called vector quantity. For example, force, velocity, acceleration, etc. All these quantities are vector quantities and are added by special method of addition.

Related Posts

Units and Measurement Notes for Class 11

• September 14, 2023

Law of Conservation of Energy with Example

• August 28, 2023

Conservation Laws in Physics

• August 26, 2023

Fundamental Forces In Nature

• August 18, 2023

Learning Materials

• Business Studies
• Combined Science
• Computer Science
• Engineering
• English Literature
• Environmental Science
• Human Geography
• Macroeconomics
• Microeconomics
• Physical Quantities

A physical quantity is a property of an object, something we can measure with instruments or even by using our senses. 

Millions of flashcards designed to help you ace your studies

• Cell Biology

Is force an elemental physical quantity?

How are derived physical quantities composed?

Define the mass of an object.

What is a scalar quantity?

What is a vector?

Is velocity composed of scalar or vector quantities?

What happens in a negative flow of charge?

Can a temperature measurement be less than zero?

How are physical quantities and units related?

Need help? Meet our AI Assistant

Need help with Physical Quantities? Ask our AI Assistant

Review generated flashcards

to start learning or create your own AI flashcards

Start learning or create your own AI flashcards

StudySmarter Editorial Team

Team Physical Quantities Teachers

• 8 minutes reading time
• Checked by StudySmarter Editorial Team
• Astrophysics
• Atoms and Radioactivity
• Circular Motion and Gravitation
• Classical Mechanics
• Conservation of Energy and Momentum
• Electric Charge Field and Potential
• Electricity
• Electricity and Magnetism
• Electromagnetism
• Electrostatics
• Energy Physics
• Engineering Physics
• Famous Physicists
• Fields in Physics
• Fundamentals of Physics
• Further Mechanics and Thermal Physics
• Geometrical and Physical Optics
• Kinematics Physics
• Linear Momentum
• Magnetism and Electromagnetic Induction
• Measurements
• Mechanics and Materials
• Medical Physics
• Modern Physics
• Nuclear Physics
• Oscillations
• Particle Model of Matter
• Physical Quantities And Units
• Converting Units
• SI Prefixes
• Standard Form Physics
• Units Physics
• Use of SI Units
• Physics of Motion
• Quantum Physics
• Rotational Dynamics
• Scientific Method Physics
• Solid State Physics
• Space Physics
• Thermodynamics
• Torque and Rotational Motion
• Translational Dynamics
• Turning Points in Physics
• Wave Optics
• Waves Physics
• Work Energy and Power

Jump to a key chapter

Two simple examples of physical quantities are the mass of an object or its temperature. We can measure both with instruments, but we can also sense them using our hands by lifting the object or touching it.

What are the different physical quantities?

There is a range of physical properties that we can measure. All these properties are related to an object ’ s dimensions or its constitution. T he seven elemental physical quantities are:

• Mass: this is the property that tells us how much matter is contained in the object. An object with a larger quantity of matter has a larger mass. Weight is the force exerted over an object ’ s mass. Mass and weight are often confused. The equation for weight is: \(weight = mass \cdot 9.81m / s ^ 2\).
• Length: this is the property that tells us how long an object is. This property is related to the properties of area and volume.
• Time: this property is related to the flow of events, and it always increases. Like mass, time is one of the properties that cannot be negative. Time tells us the flow of things in the universe.
• Electrical charge: this is a physical quantity that can be positive or negative, only affecting polarity. It causes a force to act upon the matter when placed in an electric field.
• Temperature: this is the property that measures the quantity of heat in a substance or object. Heat is related to the movement of the particles in the object.
• Mole: this is a fixed physical quantity that measures the number of molecules in a substance. The property represents an exact number of particles or molecules equal to \(6.02214076 \cdot 10 ^ {23}\) molecules of the substance.
• Luminosity: this is an energy measure, just like temperature. Luminosity measures the quantity of electromagnetic energy emitted by an object as light per unit time.

The difference between weight and mass

People confuse weight and mass all the time. The best way to explain the difference is by using an example featuring a ball.

A ball has a different weight on Mars than it does on Earth. However, the matter that composes the ball remains the same. And i f the matter does not change, then neither does the mass.

Weight is the amount of force that gravity exerts on mass; it is force per mass . A scale, therefore, measures the gravitational force that pulls down the mass of an object.

This can also be explained using the gravity force formula that determines the weight of an object:

\[\text{weight} = \text{mass} \cdot \text{gravity}\]

The amount of matter in the ball does not change, so mass is a constant. T he main difference is the gravity because gravity on Earth is higher than gravity on Mars:

\[\text{gravity (Earth)} > \text{gravity(Mars)}\]

Therefore, the weight on Earth will be higher than on Mars:

\[\text{mass} \cdot \text{gravity (Earth)} > \text{mass} \cdot \text{gravity(Mars)}\]

What are extensive and intensive quantities?

Physical quantities have two categories: extensive quantities and intensive quantities. This classification is related to an object ’ s mass. Extensive quantities depend on an object ’ s mass or size, while intensive quantities do not.

Examples of extensive physical quantities

Mass and electrical charge are examples of extensive physical quantities.

Mass depends on the size of the object. If you have two weights made of steel and one is double the size of the other, the larger one will have double the mass.

Another example concerns electrical charge. If the particles of an object have some electrical charge, their number tells us how much electrical charge the object has. If the object increases its mass, thus increasing its number of particles, the electrical charge will be larger.

Examples of intensive physical quantities

Intensive physical quantities do not depend on the object ’ s mass or size. Simple examples of this are time and temperature.

We can measure the time it takes for two objects of different mass to move from position A to position B. In both cases, time flows in the same way, independent of the composition or size of the objects.

Imagine we have an object with a temperature of 100 Kelvin, which we divide in half. In ideal circumstances where there is no heat transfer , the two halves will each still have the same temperature of 100 K.

What are derived physical quantities?

Derived physical quantities are the properties of an object that result from two elemental physical quantities. Derived quantities can result from a relationship of the same physical quantity (e.g. area) or by relating two different ones (e.g. velocity). See below for some examples of derived physical quantities.

Area and volume: related to length:

\[Area = length \cdot width; \space Volume = length \cdot width \cdot height\]

Velocity and acceleration : related to length and time:

\[Velocity = \frac{length}{time}; \space Acceleration = \frac{length}{time^2}\]

Density : related to length and mass:

\[Density = \frac{mass}{length^3}\]

Weight: related to acceleration and mass (i n a planet, acceleration is its gravitational acceleration):

\[Weight = gravity \cdot mass\]

Pressure : related to force and length (f or pressure , the force can be the weight exerted by an object, and the area over which this force acts is related to length):

\[Pressure = \frac{force}{length^2}\]

What are some characteristics of physical quantities?

Physical quantities have several characteristics related to their properties, s ome of which are listed below.

• No physical quantity can be less than zero, except for electrical charge and temperature values.
• Some physical quantities can have a value of zero, such as electrical charge or mass. In these cases, the object is electrically neutral (has no charge) or is massless ( light ).
• Some physical quantities are scalar, which means that they have only a value but no direction. Examples of these quantities are volume, mass, and mole.
• Other physical quantities are vectorial, in which case you need the direction to understand what is happening. Examples of vectorial quantities are velocity and acceleration .

Temperatures below zero are the result of taking the temperature at which water freezes as a zero (0) value. In Celsius, every temperature below the freezing point of water is negative.

How are units and physical quantities linked?

Physical quantities are important because they allow us to describe an object. Objects have a certain mass, a certain length, and a certain amount of atoms. The units are the values of reference we use to measure the properties of objects.

Imagine measuring the weight of two rocks. You can tell by holding them in your hands that one is heavier than the other. However, to determine their precise weight, you need to compare them against a standard value (unit), in this case, the kilogram.

Physical Quantities - Key takeaways

• Physical quantities and units are different. P hysical quantities are an object ’ s physical properties, while units are a reference we use to measure the object ’ s properties.
• There are two types of physical quantities, elemental quantities and derived quantities. The derived ones are composed of the elemental quantities.
• The seven elemental physical quantities are mass, time, temperature, mole, length, luminosity, and electrical charge.
• Some derived physical quantities are velocity, heat, density , pressure, and momentum .
• Extensive physical quantities depend on the amount of substance or the size of the object.
• Intensive physical quantities do not depend on the amount of substance or the size of the object.
• Physical quantities are directly related to the units in physics .

Flashcards in Physical Quantities 9

No, it isn’t.

Derived physical quantities are composed of elemental physical quantities.

Mass is the amount of matter in an object.

A scalar quantity can be described without knowing its direction. The quantity is called a magnitude and is just a number.

A vector is a quantity where you need the direction and value to know what is happening. The value of the quantity is known as magnitude.

Velocity is composed of length and time. Both are scalar quantities.

Learn with 9 Physical Quantities flashcards in the free StudySmarter app

We have 14,000 flashcards about Dynamic Landscapes.

Already have an account? Log in

Frequently Asked Questions about Physical Quantities

What is a physical quantity?

A physical quantity is a quantity that is used to describe the properties of an object.

What is a vector quantity in physics?

A vector quantity is a physical quantity with a value and a direction. An example of this is velocity. You need the velocity value and its direction to know what is happening.

What are fundamental physical quantities?

A fundamental physical quantity is one of the seven elemental quantities that describe the properties of an object. They are temperature, mass, length, electrical charge, mole, luminosity, and time.

What are the types of physical quantities?

Physical quantities can be extensive or intensive. They are extensive if they depend on the mass or size of the object and intensive if they do not.

Test your knowledge with multiple choice flashcards

Join the StudySmarter App and learn efficiently with millions of flashcards and more!

That was a fantastic start, you can do better, sign up to create your own flashcards.

Access over 700 million learning materials

Study more efficiently with flashcards

Get better grades with AI

Already have an account? Log in  

Keep learning, you are doing great.

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter is a globally recognized educational technology company, offering a holistic learning platform designed for students of all ages and educational levels. Our platform provides learning support for a wide range of subjects, including STEM, Social Sciences, and Languages and also helps students to successfully master various tests and exams worldwide, such as GCSE, A Level, SAT, ACT, Abitur, and more. We offer an extensive library of learning materials, including interactive flashcards, comprehensive textbook solutions, and detailed explanations. The cutting-edge technology and tools we provide help students create their own learning materials. StudySmarter’s content is not only expert-verified but also regularly updated to ensure accuracy and relevance.

Team Physics Teachers

Study anywhere. Anytime.Across all devices.

Create a free account to save this explanation..

Save explanations to your personalised space and access them anytime, anywhere!

By signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.

Sign up to highlight and take notes. It’s 100% free.

Join over 22 million students in learning with our StudySmarter App

The first learning app that truly has everything you need to ace your exams in one place

• Flashcards & Quizzes
• AI Study Assistant
• Study Planner
• Smart Note-Taking

• IIT JEE Study Material
• Units And Dimensions

Units and Dimensions - Dimensional Formula

Introduction to units and dimensions.

Every measurement has two parts. The first is a number (n), and the next is a unit (u). Q = nu. For example, the length of an object = 40 cm. The number expressing the magnitude of a physical quantity is inversely proportional to the unit selected.

Download Complete Chapter Notes of Units and Measurements Download Now

If n 1 and n 2 are the numerical values of a physical quantity corresponding to the units u 1 and u 2 , then n 1 u 1 = n 2 u 2 . For example, 2.8 m = 280 cm; 6.2 kg = 6200 g.

Table of Contents

• What Is the Dimensional Formula?
• Limitations
• Physical Constants

Dimensional Formulas for Physical Quantities

• Quantities with the Same Dimensional Formula
• Applications

Fundamental and Derived Quantities

• The quantities that are independent of other quantities are called fundamental quantities . The units that are used to measure these fundamental quantities are called fundamental units . There are four systems of units, namely CGS, MKS, FPS and SI.
• The quantities that are derived using the fundamental quantities are called derived quantities . The units that are used to measure these derived quantities are called derived units .

Fundamental and supplementary physical quantities in the SI system

Supplementary Quantities

Most SI units are used in scientific research. SI is a coherent system of units.

A coherent system of units is one in which the units of derived quantities are obtained as multiples or submultiples of certain basic units. The SI system is a comprehensive, coherent and rationalised MKS. The ampere system (RMKSA system) was devised by Prof. Giorgi.

• Meter: A meter is equal to 1650763.73 times the wavelength of the light emitted in a vacuum due to the electronic transition from 2p 10 state to 5d 5 state in Krypton-86. But in 1983, the 17 th General Assembly of Weights and Measures adopted a new definition for the meter in terms of the velocity of light. According to this definition, a meter is defined as the distance travelled by light in a vacuum during a time interval of 1/299, 792, 458 of a second.
• Kilogram : The mass of a cylinder of platinum-iridium alloy kept in the International Bureau of Weights and Measures preserved at Serves near Paris is called one kilogram.
• Second : The duration of 9192631770 periods of radiation corresponding to the transition between the two hyperfine levels of the ground state of cesium-133 atoms is called one second.
• Ampere: The current which, when flowing in each of two parallel conductors of infinite length and negligible cross-section and placed one meter apart in vacuum, causes each conductor to experience a force of 2 × 10 -7 newtons per meter of length is known as one ampere .
• Kelvin : The fraction of 1/273.16 of the thermodynamic temperature of the triple point of water is called Kelvin.
• Candela : The luminous intensity in the perpendicular direction of a surface of a black body of area 1/600000 m 2 at the temperature of solidifying platinum under a pressure of 101325 Nm -2 is known as one candela.
• Mole : The amount of a substance of a system which contains as many elementary entities as there are atoms in 12 × 10 -3 kg of carbon-12 is known as one mole .
• Radian: The angle made by an arc of the circle equivalent to its radius at the centre is known as a radian. 1 radian = 57 o 17 l 45 ll .
• Steradian : The angle subtended at the centre by one square meter area of the surface of a sphere of radius one meter is known as steradian.

Some Important Conclusions

• Angstrom is the unit of length used to measure the wavelength of light. 1 Å = 10 -10 m.
• Fermi is the unit of length used to measure nuclear distances. 1 Fermi = 10 -15 meter.
• A light year is the unit of length for measuring astronomical distances.
• Light year = distance travelled by light in 1 year = 9.4605 × 10 15 m.
• Astronomical unit = Mean distance between the sun and earth = 1.5 × 10 11 m.
• Parsec = 3.26 light years = 3.084×10 16 m.
• Barn is the unit of area for measuring scattering cross-section of collisions. 1 barn = 10 -28 m 2 .
• Chronometer and metronome are time-measuring instruments. The quantity having the same unit in all the systems of units is time.

⇒ Also Read: List of All SI Units

Note: The following are not used in the SI system.

• deca 10 1 deci 10 -1
• hecta 10 2 centi 10 -2

How to Write Units of Physical Quantities?

1. Full names of the units, even when they are named after a scientist, should not be written with a capital letter. For example, newton, watt, ampere, meter

2. The unit should be written either in full or in agreed symbols only

3. Units do not take the plural form. For example, 10 kg but not 10 kgs, 20 w but not 20 ws

4. No full stop or punctuation mark should be used within or at the end of symbols for units. For example, 10 W but not 10 W.

What Are Dimensions?

Dimensions of a physical quantity are the powers to which the fundamental units are raised to obtain one unit of that quantity.

Dimensional Analysis

Dimensional analysis is the practice of checking relations between physical quantities by identifying the dimensions of the physical quantities. These dimensions are independent of the numerical multiples and constants, and all the quantities in the world can be expressed as a function of the fundamental dimensions.

Read More: Dimensional Analysis

Dimensional Formula

The expression showing the powers to which the fundamental units are to be raised to obtain one unit of a derived quantity is called the dimensional formula of that quantity.

If Q is the unit of a derived quantity represented by Q = M a L b T c , then M a L b T c is called the dimensional formula, and the exponents a, b, and c are called dimensions.

What Are Dimensional Constants?

The physical quantities with dimensions and a fixed value are called dimensional constants. For example, gravitational constant (G), Planck’s constant (h), universal gas constant (R), velocity of light in a vacuum (C), etc.

What Are Dimensionless Quantities? 

Dimensionless quantities are those which do not have dimensions but have a fixed value.

• Dimensionless quantities without units:  Pure numbers, π, e, sin θ, cos θ, tan θ etc.
• Dimensionless quantities with units: Angular displacement – radian, Joule’s constant – joule/calorie, etc.

What Are Dimensional Variables?

Dimensional variables are those physical quantities which have dimensions and do not have a fixed value. For example, velocity, acceleration, force, work, power, etc.

What Are the Dimensionless Variables?

Dimensionless variables are those physical quantities which do not have dimensions and do not have a fixed value. For example, specific gravity, refractive index , the coefficient of friction, Poisson’s ratio, etc.

Law of Homogeneity of Dimensions

• In any correct equation representing the relation between physical quantities, the dimensions of all the terms must be the same on both sides. Terms separated by ‘+’ or ‘–’ must have the same dimensions.
• A physical quantity Q has dimensions a, b and c in length (L), mass (M) and time (T), respectively, and n 1 is its numerical value in a system in which the fundamental units are L 1 , M 1 and T 1 and n 2 is the numerical value in another system in which the fundamental units are L 2 , M 2 and T 2, respectively, then

Limitations of Dimensional Analysis

• Dimensionless quantities cannot be determined by this method. Also, the constant of proportionality cannot be determined by this method. They can be found either by experiment (or) by theory.
• This method does not apply to trigonometric, logarithmic and exponential functions .
• This method will be difficult in the case of physical quantities, which are dependent upon more than three physical quantities.
• In some cases, the constant of proportionality also possesses dimensions. In such cases, we cannot use this system.
• If one side of the equation contains the addition or subtraction of physical quantities, we cannot use this method to derive the expression.

Some Important Conversions

• 1 bar = 10 6 dyne/cm 2 = 10 5 Nm -2 = 10 5 pascal
• 76 cm of Hg = 1.013×10 6 dyne/cm 2   = 1.013×10 5 pascal = 1.013 bar.
• 1 toricelli or torr = 1 mm of Hg = 1.333×10 3 dyne/cm 2  = 1.333 millibar.
• 1 kmph = 5/18 ms -1
• 1 dyne = 10 -5 N,
• 1 H.P = 746 watt
• 1 kilowatt hour = 36×10 5 J
• 1 kgwt = g newton
• 1 calorie = 4.2 joule
• 1 electron volt = 1.602×10 -19 joule
• 1 erg = 10 -7 joule

Some Important Physical Constants

• Velocity of light in vacuum (c) = 3 × 10 8 ms -1
• Velocity of sound in air at STP = 331 ms -1
• Acceleration due to gravity (g) = 9.81 ms -2
• Avogadro number (N) = 6.023 × 10 23 /mol
• Density of water at 4 o C = 1000 kgm -3 or 1 g/cc.
• Absolute zero = -273.15 o C or 0 K
• Atomic mass unit = 1.66 × 10 -27 kg
• Quantum of charge (e) = 1.602 × 10 -19 C
• Stefan’s constant = 5.67 × 10 –8 W/m 2 /K 4
• Boltzmann’s constant (K) = 1.381 × 10 -23 JK -1
• One atmosphere = 76 cm Hg = 1.013 × 10 5 Pa
• Mechanical equivalent of heat (J) = 4.186 J/cal
• Planck’s constant (h) = 6.626 × 10 -34 Js
• Universal gas constant (R) = 8.314 J/mol–K
• Permeability of free space (μ 0 ) = 4π × 10 -7 Hm -1
• Permittivity of free space (ε 0 ) = 8.854 × 10 -12 Fm -1
• The density of air at S.T.P. = 1.293 kg m -3
• Universal gravitational constant = 6.67 × 10 -11 Nm 2 kg -2

Derived SI units with Special Names

Quantities Having the Same Dimensional Formula

• Impulse and momentum.
• Work, torque, the moment of force, energy.
• Angular momentum, Planck’s constant, rotational impulse.
• Stress, pressure, modulus of elasticity, energy density.
• Force constant, surface tension, surface energy.
• Angular velocity, frequency, velocity gradient.
• Gravitational potential, latent heat.
• Thermal capacity, entropy, universal gas constant and Boltzmann’s constant.
• Force, thrust.
• Power, luminous flux.

Applications of Dimensional Analysis

Dimensional analysis is very important when dealing with physical quantities. In this section, we will learn about some applications of dimensional analysis.

Fourier laid down the foundations of dimensional analysis. The dimensional formulas are used to:

• Verify the correctness of a physical equation.
• Derive a relationship between physical quantities.
• Converting the units of a physical quantity from one system to another system.

Checking the Dimensional Consistency

As we know, only similar physical quantities can be added or subtracted. Thus, two quantities having different dimensions cannot be added together. For example, we cannot add mass and force or electric potential and resistance.

For any given equation, the principle of homogeneity of dimensions is used to check the correctness and consistency of the equation. The dimensions of each component on either side of the sign of equality are checked, and if they are not the same, the equation is considered wrong.

Let us consider the equation given below,

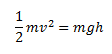
The dimensions of the LHS and the RHS are calculated

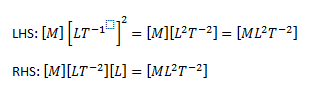
As we can see, the dimensions of the LHS and the RHS are the same. Hence, the equation is consistent.

Deducing the Relation among Physical Quantities

Dimensional analysis is also used to deduce the relation between two or more physical quantities. If we know the degree of dependence of a physical quantity on another, that is, the degree to which one quantity changes with the change in another, we can use the principle of consistency of two expressions to find the equation relating to these two quantities. This can be understood more easily through the following illustration.

Example: Derive the formula for  centripetal force  F acting on a particle moving in a uniform circle.

As we know, the centripetal force acting on a particle moving in a uniform circle depends on its mass m, velocity v and the radius r of the circle. Hence, we can write

F = m a v b r c

Writing the dimensions of these quantities,

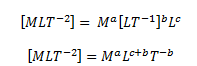
As per the principle of homogeneity, we can write,

a = 1, b + c = 1 and b = 2

Solving the above three equations, we get, a = 1, b = 2 and c = -1.

Hence, the centripetal force F can be represented as,

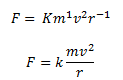
Recommended Videos

Units & dimensions – vernier calliper’s.

Units & Dimensions – Screw Gauge

Units & Dimensions – Important Questions

Units & Dimensions – Introduction Concepts

Units & Dimensions – SI System and Parallax

Frequently Asked Questions on Units and Dimensions

What is the meaning of dimension in physics.

It is an expression that relates derived quantities to fundamental quantities. But it is not related to the magnitude of the derived quantity.

What is the dimension of force?

We know that, F = ma —– (1) Mass is a fundamental quantity, but acceleration is a derived quantity and can be represented in terms of fundamental quantities. a = [LT −2 ] —– (2) Using (1) and (2), F = [MLT −2 ] This is the dimension of force.

What is dimensional analysis?

Dimensional analysis is based on the principle that two quantities can be compared only if they have the same dimensions. For example, I can compare kinetic energy with potential energy and say they are equal, or one is greater than another because they have the same dimension. But I cannot compare kinetic energy with force or acceleration as their dimensions are different.

How do you demonstrate dimensional analysis with an example?

Suppose I have the following equation, F = E a .V b . Tc Where, F = Force; E = Energy; V = Velocity; M = Mass We need to find the value of a, b and c. Following are the dimensions of the given quantities, F = [MLT −2 ], E = [ML 2 T −2 ], V = [LT −1 ] According to dimensional analysis, the dimension of RHS should be equal to LHS; hence, [MLT −2 ] = [ML 2 T −2 ] a . [LT −1 ] b . [T] c [MLT −2 ] = [M a L 2a+b T −2a−b+c ] Now, we have three equations, a = 1 2a+b = 1 −2a − b + c = −2 Solving the three equations, we get, a = 1, b = −1 and c = −1.

What is meant by a unit?

The standard quantity with which a physical quantity of the same kind is compared is called a unit.

Why are mass, length, and time chosen as fundamental or base quantities in mechanics?

This is because mass, length and time are independent of each other. All the other quantities in mechanics can be expressed in terms of mass, length and time.

Define significant figures.

Significant figures are those digits in a number known with certainty plus one more uncertain number.

Define dimensions.

The dimensions of a physical quantity are the powers to which the fundamental quantities are raised to represent that physical quantity.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Clear cut explanation. All my confusions are cleared.

This piece of information is very helpful. Thank you

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Units And Dimensions
• Active page

Units And Dimensions of Class 11

The dimension of a physical quantity are the powers to which the fundamental (or base) quantities like mass, length and time etc. have to be raised to represent the quantity. Consider the physical quantity “ Force ”. The unit of force is Newton. Read NCERT textbook and try to solve all questions given in exercise before solving additional questions, take help form NCERT Solutions for class 11 Physics .

1 Newton = 1 kg m/sec 2

 kg → M 1 (Mass);  3 → L 1 (Length);  s- 2 → T -2 (Time)

∴ Dimensions of force are [M 1 L 1 T -2 ]

Dimensional formula for some Physical quantities

Q16. Write the dimensions of: Impulse, Pressure, Work, Universal constant of Gravitation.

(i) [M 1 L 1 T −1 ]

(ii) [M 2 L 2 T −2 ]

(iii) [M 1 L 2 T −2 ]

(iv) [M -1 L 3 T −2 ]

Four types of quantities

Dimensional constant: These are the quantities whose values are constant and they possess dimensions. For example, velocity of light in vacuum, universal gas constant etc.

Dimensional variables: These are the quantities whose values are variable, and they possess dimensions. For example, area, volume, density etc.

Dimensionless constants: These are the quantities whose values are constant, but they do not possess dimensions. For example, π, 1, 2, 3, ….. etc.

Dimensionless Variables: These are the quantities, whose values are variable, and they do not have dimensions, e.g., angle, strain, specific gravity etc.

Uses of dimensions:

(1) Checking the correctness (dimensional consistency) of an equation: An equation contains several terms which are separated from each other by symbols of equality, plus or minus. The dimensions of all the terms in an equation must be identical. This means that we can not add velocity to force. This principle is called Principle of Homogeneity of dimensions.

Look at the equation :

v 2 = u 2 + 2as

The equation v 2 = u 2 + 2as is dimensionally consistent, or dimensionally correct.

A dimensionally correct equation may not be actually correct. For example, the equation v 2 = u 2 + 3as is also dimensionally correct but we know that it is not actually correct. However, all correct equations must necessarily be dimensionally correct.

Q17 . Which of the following equations may be correct ?

(v) V = √GMR

Given: G = Gravitational constant, whose dimensions are [M −1 L 3 T −2 ] M 1 ,M 2 and M have dimensions of mass. L, x, r, R has dimensssions of length. And t has dimensions of Time. ‘F’ denotes Force and ‘a’ has dimensions of acceleration.

(i) Yes (ii) Yes (iii) No (iv) Yes (v) No.

(2) Conversion of units: Dimensional methods are useful in finding the conversion factor for changing the units to a different set of base quantities. Let us consider one example, the SI unit of force is Newton. The CGS unit of force is dyne. How many dynes is equal to one newton. Now,

1 newton = [F] = [M 1 L 1 T -2 ] = (1kg) 1 (1 meter) 1 (1s) -2

1 dyne = (1g)(1 cm) (1s) -2

1 newton = 10 5 dynes

Thus knowing the conversion factors for the base quantities, one can work out the conversion factor of any derived quantity if the dimensional formula of the derived quantity is known.

Q18. Find the conversion factor for expressing universal gravitational constant from SI units to cgs units.

Solution:   6.67 x 10 -8 cm 3 s -2 g-1

(3) Deducing relation among the physical quantities:

Suppose we have to find the relationship connecting a set of physical quantities as a product type of dependence. Then dimensional analysis can be used as a tool to find the required relation. Let us consider one example. Suppose we have to find the relationship between gravitational potential energy of a body in terms of its mass ‘m’, height ‘h’ from the earth’s surface and acceleration due to gravity ‘g’, then,

Let us assume that: − Gravitational potential energy, U,

where K, a, b, and c are dimensionless constants.

∴ a = 1, b + c = 2

−2b = −2

b = 1, c = 1.

U = Kmgh, where K is a dimensionless constant.

Thus by dimensional analysis, we conclude that the gravitational potential energy of a body is directly proportional to its mass, acceleration due to gravity and its height from the surface of the earth.

Limitations of dimensional analysis:

This method does not give us any information about the dimensionless constants appearing in the derived formula, e.g. 1, 2, 3, .. .π  etc.

We can’t derive the formula having trigonometrical functions, exponential functions etc, which have no dimensions.

The method of dimensions cannot be used to derive an exact form of relation when it consists of more that one part on any side, e.g. the formula v 2 = u 2 + 2as cannot be obtained.

If a quantity depends on more than three factors having dimensions the formula cannot be derived. This is because on equating powers of M, L and T on either side of the dimensional equation, we can obtain three equations from which only three exponents can be calculated.

It gives no information whether a physical quantity is a scalar or a vector.

Q19. Using the method of dimensions, find the acceleration of a particle moving with a constant speed v in a circle of radius r.

Solution: Assuming that the acceleration of a particle depends on v and r

a ∝ v x r y ⇒ a = k v x r y

Now as we know dimensions of acceleration (a) = M°LT −2

and dimensions of velocity (v) = M ° LT −1

dimension of radius (r) = M ° LT °

Putting all three dimensions in (1), we get

M ° LT −2 = k (M ° LT −1 )x (M ° LT ° )y

M ° LT −2 = k M ° Lx + YT − x

Comparing the powers, we get

∴y = 1−2 = −1

∴ a = k v 2 r −1

a = kv 2 /r

P is pressure and V is the volume. Calculate the dimensions of a and b.

Solution: Only physical quantities having same dimensions are added or subtracted. So a/v 2 has the same dimensions as that of pressure.

As pressure = Force/Area

Dimensions of a

Similarly dimensions of b is same as that of volume.

Solution: Yes, this expression is dimensionally correct, yet it appears to be incorrect. As we are taking it to be for n th second. Here one second is divided through the equation.  

Q22. Find the dimensions of resistivity, thermal conductivity and coefficient of viscosity.

(ii) Thermal conductivity, k

(iii) Coefficient of viscosity,

Q23. A displacement of a particle is given by equation y = A sin ωt, where y is in metres and A is also in metres, t is in seconds. What are the dimensions of ω.

Solution: As the angles are always dimensionless, so

ωt = dimensionless quantity

Dimensions of ωt = M ° L ° T °

Dimensions of ω = M ° L°T −1

Q24. If density ρ, acceleration due to gravity g and frequency f are the basic quantities, find the dimensions of force.

Solution: We have ρ = ML −3 ,g = LT −2 f = T −1

Solving for M, L and T in terms of ρ, g and f , we get

M = ρ2g3f −6 , L = gf −2 & T = f −1

Force = [MLT −2 ] = [ρg 3 f −6 .gf −2 . f 2 ] = [ρg 4 f −6 ]

Q25. An athlete’s coach told his team that muscle times speed equals power. What dimensions does he view for “muscle”?

(B) ML 2 T −2

(C) ML T –2

Solution: Power = force ´ velocity

= muscle times speed

∴ muscle represents force

muscle = [MLT −2 ]

Correct answer is (C)

Q26. If force, length and time would have been the fundamental units what would have been the dimensional formula for mass

(A) FL −1 T −2

(B) FL −1 T 2

(C) FL T −2

Solution:  Let M = K F a L b T c

= [MLT − 2] a [L b ] T c = [M a L (a+b) T (−2a+c) ]

a = 1, a + b = 0 & – 2a + c = 0

⇒ a = 1, b = – 1, c = 2

Correct answer is (B)

Q27. The dimensions of the Rydberg constant are

(A) M ° L −1 T

(B) MLT −1

(C) M ° L −1 T °

(D) ML ° T 2

Solution: From the relation

R = 1/L = L -1 = M ° L −1 T °

Correct answer is (c)

Q28. The error in the measurement of the radius of a sphere is 1%. Then error in the measurement of volume is

V = 4/3 πr 3

ΔV/V x 100 = 3(Δr/r) x 100

ANSWER TO EXERCISES

1. 1 erg = 10 −7 J

2. 5.6 + (0.2) × (3) = 6.2 cm

• Introduction
• Scope And Excitement Of Physics
• Technology And Society
• Fundamental Forces In Nature
• Conservation Laws
• Measurement And Units
• Measurement Of Mass
• Errors In Measurement
• Physical Quantities

Talk to Our counsellor

Physical Quantities and Units of Measurement

• First Online: 12 December 2023

Cite this chapter

• Maurizio Spurio 9  

Part of the book series: Undergraduate Lecture Notes in Physics ((ULNP))

660 Accesses

Physics is a discipline based on observable and measurable quantities and founded on the Galilean scientific method. Seven fundamental basic units of measurement are necessary to define all quantities used and all other units of measurement are derived. For the study of mechanics, three of the seven basic units are necessary: distances, time, and masses. In this chapter, in addition to the definition of physical dimension and of the unit of measurement, we deal about direct and indirect measures. Direct measures refer usually to distances, time intervals and masses at the human scale, but physics deals with quantities from the sub-microscopic to the cosmological worlds that needs to be measured. The chapter introduces the concepts of space, time and mass and their connection with modern physics and how physics solve the problem to measure microscopic and macroscopic distances, times, and masses.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Today, for example, we cannot rely on material simply found on the web. The data could be genuine, but could have been acquired with some form of bias which could affect the correctness of the conclusions. Normally, only information that has been peer-reviewed  (see below) should be used.

Obviously, the British disagreed.

SI stands for Système International , which is an abbreviated form of its full French name Système international d’unités .

The word atom comes from Greek atomos  that means ‘indivisible’ , based on a- ‘not’ + temnein ‘to cut’.

On the other hand, \(E=mc^2\) is the only universally known formula of physics, even if many people do not grasp its meaning.

Practical units.  Although we will always use the SI units in this book, it is important to know that there exist, and they are universally used, other units of measurement which are called practical For example, an astrophysicist struggles to measure distances in m; he prefers to use the parsec (pc), which corresponds to \( \sim 3 \times 10 ^{16} \) m, or 3 light-years (the distance traveled by light in 1 year). Similarly, particle physicists measure masses not in kilograms, but in units of MeV/c \(^2\) . If it existed, the mass of a 1 MeV/c \(^2\) particle = \(1.79\times 10^{-30}\) kg. The electron has a mass of 0.511 MeV/c \(^2\) . The proton of 938 MeV/c \(^2\) , the neutron 0.14% more than the proton.

For easily understandable military reasons, the spatial accuracy \(\Delta L\) of the GPS is limited to about 3–5 m. Since the light travels at c = 30 cm/ns, the corresponding temporal resolution is \(\Delta t= \Delta L/c \sim \) 10 ns. The GPS is actually intrinsically more accurate, up to 1–3 ns.

An alternative positioning system to GPS, called Galileo , has been developed in Europe, and is it coming into operation. It should perform better than GPS.

Provided he was born in a nation of the Western world, in an averagely wealthy family.

Those who study physics of nuclei and the Fermi theory of weak interactions which explains radioactive decay will see how to correlate the value of \(\lambda \) with the properties of nuclei.

Free neutrons are not normally available, as they are not stable particles. Because the neutron has greater mass than the proton, an isolated neutron tends to decay into a proton and other particles, as we shall see in Sect. 8.7.2 , with an average lifetime of about 15 min. Neutrons bound in nuclei have a different effective mass and do not have sufficient energy to decay.

The decay process of this isotope is illustrated in Sect. 8.7.2 .

During the lessons while writing on the blackboard, dimensional analysis is frequently used. In a written text this can be avoided, but I always suggest that the student practice dimensional analysis of more complex equations.

Note to Italian education ministers: no tunnel is needed between CERN and Gran Sasso for neutrino propagation.

Author information

Authors and affiliations.

Department of Physics and Astronomy, University of Bologna, Bologna, Italy

Maurizio Spurio

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Maurizio Spurio .

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Spurio, M. (2023). Physical Quantities and Units of Measurement. In: The Fundamentals of Newtonian Mechanics. Undergraduate Lecture Notes in Physics. Springer, Cham. https://doi.org/10.1007/978-3-031-47289-3_1

Download citation

DOI : https://doi.org/10.1007/978-3-031-47289-3_1

Published : 12 December 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-47288-6

Online ISBN : 978-3-031-47289-3

eBook Packages : Physics and Astronomy Physics and Astronomy (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

1.3 The Language of Physics: Physical Quantities and Units

Learning objectives.

By the end of this section, you will be able to do the following:

• Associate physical quantities with their International System of Units (SI) and perform conversions among SI units using scientific notation
• Relate measurement uncertainty to significant figures and apply the rules for using significant figures in calculations
• Correctly create, label, and identify relationships in graphs using mathematical relationships (e.g., slope, y -intercept, inverse, quadratic and logarithmic)

The Role of Units

Physicists, like other scientists, make observations and ask basic questions. For example, how big is an object? How much mass does it have? How far did it travel? To answer these questions, they make measurements with various instruments (e.g., meter stick, balance, stopwatch, etc.).

The measurements of physical quantities are expressed in terms of units, which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in meters (for sprinters) or kilometers (for long distance runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way ( Figure 1.13 ).

All physical quantities in the International System of Units (SI) are expressed in terms of combinations of seven fundamental physical units, which are units for: length, mass, time, electric current, temperature, amount of a substance, and luminous intensity.

SI Units: Fundamental and Derived Units

There are two major systems of units used in the world: SI units (acronym for the French Le Système International d’Unités, also known as the metric system), and English units (also known as the imperial system). English units were historically used in nations once ruled by the British Empire. Today, the United States is the only country that still uses English units extensively. Virtually every other country in the world now uses the metric system, which is the standard system agreed upon by scientists and mathematicians.

Some physical quantities are more fundamental than others. In physics, there are seven fundamental physical quantities that are measured in base or physical fundamental units: length, mass, time, electric current temperature, amount of substance, and luminous intensity. Units for other physical quantities (such as force, speed, and electric charge) described by mathematically combining these seven base units. In this course, we will mainly use five of these: length, mass, time, electric current and temperature. The units in which they are measured are the meter, kilogram, second, ampere, kelvin, mole, and candela ( Table 1.1 ). All other units are made by mathematically combining the fundamental units. These are called derived units .

The SI unit for length is the meter (m). The definition of the meter has changed over time to become more accurate and precise. The meter was first defined in 1791 as 1/10,000,000 of the distance from the equator to the North Pole. This measurement was improved in 1889 by redefining the meter to be the distance between two engraved lines on a platinum-iridium bar. (The bar is now housed at the International Bureau of Weights and Measures, near Paris). By 1960, some distances could be measured more precisely by comparing them to wavelengths of light. The meter was redefined as 1,650,763.73 wavelengths of orange light emitted by krypton atoms. In 1983, the meter was given its present definition as the distance light travels in a vacuum in 1/ 299,792,458 of a second ( Figure 1.14 ).

The Kilogram

The SI unit for mass is the kilogram (kg). It is defined to be the mass of a platinum-iridium cylinder, housed at the International Bureau of Weights and Measures near Paris. Exact replicas of the standard kilogram cylinder are kept in numerous locations throughout the world, such as the National Institute of Standards and Technology in Gaithersburg, Maryland. The determination of all other masses can be done by comparing them with one of these standard kilograms.

The SI unit for time, the second (s) also has a long history. For many years it was defined as 1/86,400 of an average solar day. However, the average solar day is actually very gradually getting longer due to gradual slowing of Earth’s rotation. Accuracy in the fundamental units is essential, since all other measurements are derived from them. Therefore, a new standard was adopted to define the second in terms of a non-varying, or constant, physical phenomenon. One constant phenomenon is the very steady vibration of Cesium atoms, which can be observed and counted. This vibration forms the basis of the cesium atomic clock . In 1967, the second was redefined as the time required for 9,192,631,770 Cesium atom vibrations ( Figure 1.15 ).

Electric current is measured in the ampere (A), named after Andre Ampere. You have probably heard of amperes, or amps , when people discuss electrical currents or electrical devices. Understanding an ampere requires a basic understanding of electricity and magnetism, something that will be explored in depth in later chapters of this book. Basically, two parallel wires with an electric current running through them will produce an attractive force on each other. One ampere is defined as the amount of electric current that will produce an attractive force of 2.7 × × 10 –7 newton per meter of separation between the two wires (the newton is the derived unit of force).

The SI unit of temperature is the kelvin (or kelvins, but not degrees kelvin). This scale is named after physicist William Thomson, Lord Kelvin, who was the first to call for an absolute temperature scale. The Kelvin scale is based on absolute zero. This is the point at which all thermal energy has been removed from all atoms or molecules in a system. This temperature, 0 K, is equal to −273.15 °C and −459.67 °F. Conveniently, the Kelvin scale actually changes in the same way as the Celsius scale. For example, the freezing point (0 °C) and boiling points of water (100 °C) are 100 degrees apart on the Celsius scale. These two temperatures are also 100 kelvins apart (freezing point = 273.15 K; boiling point = 373.15 K).

Metric Prefixes

Physical objects or phenomena may vary widely. For example, the size of objects varies from something very small (like an atom) to something very large (like a star). Yet the standard metric unit of length is the meter. So, the metric system includes many prefixes that can be attached to a unit. Each prefix is based on factors of 10 (10, 100, 1,000, etc., as well as 0.1, 0.01, 0.001, etc.). Table 1.2 gives the metric prefixes and symbols used to denote the different various factors of 10 in the metric system.

See Appendix A for a discussion of powers of 10.

The metric system is convenient because conversions between metric units can be done simply by moving the decimal place of a number. This is because the metric prefixes are sequential powers of 10. There are 100 centimeters in a meter, 1000 meters in a kilometer, and so on. In nonmetric systems, such as U.S. customary units, the relationships are less simple—there are 12 inches in a foot, 5,280 feet in a mile, 4 quarts in a gallon, and so on. Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by switching to the most-appropriate metric prefix. For example, distances in meters are suitable for building construction, but kilometers are used to describe road construction. Therefore, with the metric system, there is no need to invent new units when measuring very small or very large objects—you just have to move the decimal point (and use the appropriate prefix).

Known Ranges of Length, Mass, and Time

Table 1.3 lists known lengths, masses, and time measurements. You can see that scientists use a range of measurement units. This wide range demonstrates the vastness and complexity of the universe, as well as the breadth of phenomena physicists study. As you examine this table, note how the metric system allows us to discuss and compare an enormous range of phenomena, using one system of measurement ( Figure 1.16 and Figure 1.17 ).

More precise values are in parentheses.

Using Scientific Notation with Physical Measurements

Scientific notation is a way of writing numbers that are too large or small to be conveniently written as a decimal. For example, consider the number 840,000,000,000,000. It’s a rather large number to write out. The scientific notation for this number is 8.40 × × 10 14 . Scientific notation follows this general format

In this format x is the value of the measurement with all placeholder zeros removed. In the example above, x is 8.4. The x is multiplied by a factor, 10 y , which indicates the number of placeholder zeros in the measurement. Placeholder zeros are those at the end of a number that is 10 or greater, and at the beginning of a decimal number that is less than 1. In the example above, the factor is 10 14 . This tells you that you should move the decimal point 14 positions to the right, filling in placeholder zeros as you go. In this case, moving the decimal point 14 places creates only 13 placeholder zeros, indicating that the actual measurement value is 840,000,000,000,000.

Numbers that are fractions can be indicated by scientific notation as well. Consider the number 0.0000045. Its scientific notation is 4.5 × × 10 –6 . Its scientific notation has the same format

Here, x is 4.5. However, the value of y in the 10 y factor is negative, which indicates that the measurement is a fraction of 1. Therefore, we move the decimal place to the left, for a negative y . In our example of 4.5 × × 10 –6 , the decimal point would be moved to the left six times to yield the original number, which would be 0.0000045.

The term order of magnitude refers to the power of 10 when numbers are expressed in scientific notation. Quantities that have the same power of 10 when expressed in scientific notation, or come close to it, are said to be of the same order of magnitude. For example, the number 800 can be written as 8 × × 10 2 , and the number 450 can be written as 4.5 × × 10 2 . Both numbers have the same value for y . Therefore, 800 and 450 are of the same order of magnitude. Similarly, 101 and 99 would be regarded as the same order of magnitude, 10 2 . Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of 10 −9 m, while the diameter of the sun is on the order of 10 9 m. These two values are 18 orders of magnitude apart.

Scientists make frequent use of scientific notation because of the vast range of physical measurements possible in the universe, such as the distance from Earth to the moon ( Figure 1.18 ), or to the nearest star.

Unit Conversion and Dimensional Analysis

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook in the United States, some quantities may be expressed in liters and you need to convert them to cups. A Canadian tourist driving through the United States might want to convert miles to kilometers, to have a sense of how far away his next destination is. A doctor in the United States might convert a patient’s weight in pounds to kilograms.

Let’s consider a simple example of how to convert units within the metric system. How can we want to convert 1 hour to seconds?

Next, we need to determine a conversion factor relating meters to kilometers. A conversion factor is a ratio expressing how many of one unit are equal to another unit. A conversion factor is simply a fraction which equals 1. You can multiply any number by 1 and get the same value. When you multiply a number by a conversion factor, you are simply multiplying it by one. For example, the following are conversion factors: (1 foot)/(12 inches) = 1 to convert inches to feet, (1 meter)/(100 centimeters) = 1 to convert centimeters to meters, (1 minute)/(60 seconds) = 1 to convert seconds to minutes. In this case, we know that there are 1,000 meters in 1 kilometer.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor (1 km/1,000m) = 1, so we are simply multiplying 80m by 1:

When there is a unit in the original number, and a unit in the denominator (bottom) of the conversion factor, the units cancel. In this case, hours and minutes cancel and the value in seconds remains.

You can use this method to convert between any types of unit, including between the U.S. customary system and metric system. Notice also that, although you can multiply and divide units algebraically, you cannot add or subtract different units. An expression like 10 km + 5 kg makes no sense. Even adding two lengths in different units, such as 10 km + 20 m does not make sense. You express both lengths in the same unit. See Appendix C for a more complete list of conversion factors.

Worked Example

Unit conversions: a short drive home.

Suppose that you drive the 10.0 km from your university to home in 20.0 min. Calculate your average speed (a) in kilometers per hour (km/h) and (b) in meters per second (m/s). (Note—Average speed is distance traveled divided by time of travel.)

First we calculate the average speed using the given units. Then we can get the average speed into the desired units by picking the correct conversion factor and multiplying by it. The correct conversion factor is the one that cancels the unwanted unit and leaves the desired unit in its place.

Calculate average speed. Average speed is distance traveled divided by time of travel. (Take this definition as a given for now—average speed and other motion concepts will be covered in a later module.) In equation form,

Substitute the given values for distance and time.

Convert km/min to km/h: multiply by the conversion factor that will cancel minutes and leave hours. That conversion factor is 60   min/1   h 60   min/1   h . Thus,

To check your answer, consider the following:

Be sure that you have properly cancelled the units in the unit conversion. If you have written the unit conversion factor upside down, the units will not cancel properly in the equation. If you accidentally get the ratio upside down, then the units will not cancel; rather, they will give you the wrong units as follows

which are obviously not the desired units of km/h.

• Check that the units of the final answer are the desired units. The problem asked us to solve for average speed in units of km/h and we have indeed obtained these units.
• Check the significant figures. Because each of the values given in the problem has three significant figures, the answer should also have three significant figures. The answer 30.0 km/h does indeed have three significant figures, so this is appropriate. Note that the significant figures in the conversion factor are not relevant because an hour is defined to be 60 min, so the precision of the conversion factor is perfect.
• Next, check whether the answer is reasonable. Let us consider some information from the problem—if you travel 10 km in a third of an hour (20 min), you would travel three times that far in an hour. The answer does seem reasonable.

There are several ways to convert the average speed into meters per second.

• Start with the answer to (a) and convert km/h to m/s. Two conversion factors are needed—one to convert hours to seconds, and another to convert kilometers to meters.

Multiplying by these yields

If we had started with 0.500 km/min, we would have needed different conversion factors, but the answer would have been the same: 8.33 m/s.

You may have noted that the answers in the worked example just covered were given to three digits. Why? When do you need to be concerned about the number of digits in something you calculate? Why not write down all the digits your calculator produces?

Using Physics to Evaluate Promotional Materials

A commemorative coin that is 2″ in diameter is advertised to be plated with 15 mg of gold. If the density of gold is 19.3 g/cc, and the amount of gold around the edge of the coin can be ignored, what is the thickness of the gold on the top and bottom faces of the coin?

To solve this problem, the volume of the gold needs to be determined using the gold’s mass and density. Half of that volume is distributed on each face of the coin, and, for each face, the gold can be represented as a cylinder that is 2″ in diameter with a height equal to the thickness. Use the volume formula for a cylinder to determine the thickness.

The mass of the gold is given by the formula m = ρ V = 15 × 10 − 3 g m = ρ V = 15 × 10 − 3   where ρ = 19.3 g/cc and V is the volume. Solving for the volume gives V = m ρ = 15 × 10 − 3 g 19.3  g/cc ≅ 7.8 × 10 − 4 cc.

If t is the thickness, the volume corresponding to half the gold is 1 2 ( 7.8 × 10 − 4 ) = π r 2 t = π ( 2.54 ) 2 t, where the 1″ radius has been converted to cm. Solving for the thickness gives t = ( 3.9 × 10 − 4 ) π ( 2.54 ) 2 ≅ 1.9 × 10 − 5 cm = 0.00019 mm.

The amount of gold used is stated to be 15 mg, which is equivalent to a thickness of about 0.00019 mm. The mass figure may make the amount of gold sound larger, both because the number is much bigger (15 versus 0.00019), and because people may have a more intuitive feel for how much a millimeter is than for how much a milligram is. A simple analysis of this sort can clarify the significance of claims made by advertisers.

Accuracy, Precision and Significant Figures

Science is based on experimentation that requires good measurements. The validity of a measurement can be described in terms of its accuracy and its precision (see Figure 1.19 and Figure 1.20 ). Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard piece of printer paper. The packaging in which you purchased the paper states that it is 11 inches long, and suppose this stated value is correct. You measure the length of the paper three times and obtain the following measurements: 11.1 inches, 11.2 inches, and 10.9 inches. These measurements are quite accurate because they are very close to the correct value of 11.0 inches. In contrast, if you had obtained a measurement of 12 inches, your measurement would not be very accurate. This is why measuring instruments are calibrated based on a known measurement. If the instrument consistently returns the correct value of the known measurement, it is safe for use in finding unknown values.

Precision states how well repeated measurements of something generate the same or similar results. Therefore, the precision of measurements refers to how close together the measurements are when you measure the same thing several times. One way to analyze the precision of measurements would be to determine the range, or difference between the lowest and the highest measured values. In the case of the printer paper measurements, the lowest value was 10.9 inches and the highest value was 11.2 inches. Thus, the measured values deviated from each other by, at most, 0.3 inches. These measurements were reasonably precise because they varied by only a fraction of an inch. However, if the measured values had been 10.9 inches, 11.1 inches, and 11.9 inches, then the measurements would not be very precise because there is a lot of variation from one measurement to another.

The measurements in the paper example are both accurate and precise, but in some cases, measurements are accurate but not precise, or they are precise but not accurate. Let us consider a GPS system that is attempting to locate the position of a restaurant in a city. Think of the restaurant location as existing at the center of a bull’s-eye target. Then think of each GPS attempt to locate the restaurant as a black dot on the bull’s eye.

In Figure 1.21 , you can see that the GPS measurements are spread far apart from each other, but they are all relatively close to the actual location of the restaurant at the center of the target. This indicates a low precision, high accuracy measuring system. However, in Figure 1.22 , the GPS measurements are concentrated quite closely to one another, but they are far away from the target location. This indicates a high precision, low accuracy measuring system. Finally, in Figure 1.23 , the GPS is both precise and accurate, allowing the restaurant to be located.

Uncertainty

The accuracy and precision of a measuring system determine the uncertainty of its measurements. Uncertainty is a way to describe how much your measured value deviates from the actual value that the object has. If your measurements are not very accurate or precise, then the uncertainty of your values will be very high. In more general terms, uncertainty can be thought of as a disclaimer for your measured values. For example, if someone asked you to provide the mileage on your car, you might say that it is 45,000 miles, plus or minus 500 miles. The plus or minus amount is the uncertainty in your value. That is, you are indicating that the actual mileage of your car might be as low as 44,500 miles or as high as 45,500 miles, or anywhere in between. All measurements contain some amount of uncertainty. In our example of measuring the length of the paper, we might say that the length of the paper is 11 inches plus or minus 0.2 inches or 11.0 ± 0.2 inches. The uncertainty in a measurement, A , is often denoted as δA ("delta A "),

The factors contributing to uncertainty in a measurement include the following:

• Limitations of the measuring device
• The skill of the person making the measurement
• Irregularities in the object being measured
• Any other factors that affect the outcome (highly dependent on the situation)

In the printer paper example uncertainty could be caused by: the fact that the smallest division on the ruler is 0.1 inches, the person using the ruler has bad eyesight, or uncertainty caused by the paper cutting machine (e.g., one side of the paper is slightly longer than the other.) It is good practice to carefully consider all possible sources of uncertainty in a measurement and reduce or eliminate them,

Percent Uncertainty

One method of expressing uncertainty is as a percent of the measured value. If a measurement, A , is expressed with uncertainty, δ A , the percent uncertainty is

Calculating Percent Uncertainty: A Bag of Apples

A grocery store sells 5-lb bags of apples. You purchase four bags over the course of a month and weigh the apples each time. You obtain the following measurements:

• Week 1 weight: 4. 8     lb 4. 8     lb
• Week 2 weight: 5.3     lb 5.3     lb
• Week 3 weight: 4. 9     lb 4. 9     lb
• Week 4 weight: 5.4     lb 5.4     lb

You determine that the weight of the 5 lb bag has an uncertainty of ±0.4 lb. What is the percent uncertainty of the bag’s weight?

First, observe that the expected value of the bag’s weight, A A , is 5 lb. The uncertainty in this value, δ A δ A , is 0.4 lb. We can use the following equation to determine the percent uncertainty of the weight

Plug the known values into the equation

We can conclude that the weight of the apple bag is 5 lb ± 8 percent. Consider how this percent uncertainty would change if the bag of apples were half as heavy, but the uncertainty in the weight remained the same. Hint for future calculations: when calculating percent uncertainty, always remember that you must multiply the fraction by 100 percent. If you do not do this, you will have a decimal quantity, not a percent value.

Uncertainty in Calculations

There is an uncertainty in anything calculated from measured quantities. For example, the area of a floor calculated from measurements of its length and width has an uncertainty because the both the length and width have uncertainties. How big is the uncertainty in something you calculate by multiplication or division? If the measurements in the calculation have small uncertainties (a few percent or less), then the method of adding percents can be used. This method says that the percent uncertainty in a quantity calculated by multiplication or division is the sum of the percent uncertainties in the items used to make the calculation. For example, if a floor has a length of 4.00 m and a width of 3.00 m, with uncertainties of 2 percent and 1 percent, respectively, then the area of the floor is 12.0 m 2 and has an uncertainty of 3 percent (expressed as an area this is 0.36 m 2 , which we round to 0.4 m 2 since the area of the floor is given to a tenth of a square meter).

For a quick demonstration of the accuracy, precision, and uncertainty of measurements based upon the units of measurement, try this simulation . You will have the opportunity to measure the length and weight of a desk, using milli- versus centi- units. Which do you think will provide greater accuracy, precision and uncertainty when measuring the desk and the notepad in the simulation? Consider how the nature of the hypothesis or research question might influence how precise of a measuring tool you need to collect data.

Precision of Measuring Tools and Significant Figures

An important factor in the accuracy and precision of measurements is the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. For example, consider measuring the thickness of a coin. A standard ruler can measure thickness to the nearest millimeter, while a micrometer can measure the thickness to the nearest 0.005 millimeter. The micrometer is a more precise measuring tool because it can measure extremely small differences in thickness. The more precise the measuring tool, the more precise and accurate the measurements can be.

When we express measured values, we can only list as many digits as we initially measured with our measuring tool (such as the rulers shown in Figure 1.24 ). For example, if you use a standard ruler to measure the length of a stick, you may measure it with a decimeter ruler as 3.6 cm. You could not express this value as 3.65 cm because your measuring tool was not precise enough to measure a hundredth of a centimeter. It should be noted that the last digit in a measured value has been estimated in some way by the person performing the measurement. For example, the person measuring the length of a stick with a ruler notices that the stick length seems to be somewhere in between 36 mm and 37 mm. He or she must estimate the value of the last digit. The rule is that the last digit written down in a measurement is the first digit with some uncertainty. For example, the last measured value 36.5 mm has three digits, or three significant figures. The number of significant figures in a measurement indicates the precision of the measuring tool. The more precise a measuring tool is, the greater the number of significant figures it can report.

Special consideration is given to zeros when counting significant figures. For example, the zeros in 0.053 are not significant because they are only placeholders that locate the decimal point. There are two significant figures in 0.053—the 5 and the 3. However, if the zero occurs between other significant figures, the zeros are significant. For example, both zeros in 10.053 are significant, as these zeros were actually measured. Therefore, the 10.053 placeholder has five significant figures. The zeros in 1300 may or may not be significant, depending on the style of writing numbers. They could mean the number is known to the last zero, or the zeros could be placeholders. So 1300 could have two, three, or four significant figures. To avoid this ambiguity, write 1300 in scientific notation as 1.3 × 10 3 . Only significant figures are given in the x factor for a number in scientific notation (in the form x × 10 y x × 10 y ). Therefore, we know that 1 and 3 are the only significant digits in this number. In summary, zeros are significant except when they serve only as placeholders. Table 1.4 provides examples of the number of significant figures in various numbers.

Significant Figures in Calculations

When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value. There are two different rules, one for multiplication and division and another rule for addition and subtraction, as discussed below.

For multiplication and division: The answer should have the same number of significant figures as the starting value with the fewest significant figures. For example, the area of a circle can be calculated from its radius using A = π r 2 A = π r 2 . Let us see how many significant figures the area will have if the radius has only two significant figures, for example, r = 2.0 m. Then, using a calculator that keeps eight significant figures, you would get

But because the radius has only two significant figures, the area calculated is meaningful only to two significant figures or

even though the value of π π is meaningful to at least eight digits.

For addition and subtraction : The answer should have the same number places (e.g. tens place, ones place, tenths place, etc.) as the least-precise starting value. Suppose that you buy 7.56 kg of potatoes in a grocery store as measured with a scale having a precision of 0.01 kg. Then you drop off 6.052 kg of potatoes at your laboratory as measured by a scale with a precision of 0.001 kg. Finally, you go home and add 13.7 kg of potatoes as measured by a bathroom scale with a precision of 0.1 kg. How many kilograms of potatoes do you now have, and how many significant figures are appropriate in the answer? The mass is found by simple addition and subtraction:

The least precise measurement is 13.7 kg. This measurement is expressed to the 0.1 decimal place, so our final answer must also be expressed to the 0.1 decimal place. Thus, the answer should be rounded to the tenths place, giving 15.2 kg. The same is true for non-decimal numbers. For example,

We cannot report the decimal places in the answer because 2 has no decimal places that would be significant. Therefore, we can only report to the ones place.

It is a good idea to keep extra significant figures while calculating, and to round off to the correct number of significant figures only in the final answers. The reason is that small errors from rounding while calculating can sometimes produce significant errors in the final answer. As an example, try calculating 5,098 − ( 5.000 ) × ( 1,010 ) 5,098 − ( 5.000 ) × ( 1,010 ) to obtain a final answer to only two significant figures. Keeping all significant during the calculation gives 48. Rounding to two significant figures in the middle of the calculation changes it to 5,100 – (5 .000) × (1,000) = 100, 5,100 – (5 .000) × (1,000) = 100, which is way off. You would similarly avoid rounding in the middle of the calculation in counting and in doing accounting, where many small numbers need to be added and subtracted accurately to give possibly much larger final numbers.

Significant Figures in this Text

In this textbook, most numbers are assumed to have three significant figures. Furthermore, consistent numbers of significant figures are used in all worked examples. You will note that an answer given to three digits is based on input good to at least three digits. If the input has fewer significant figures, the answer will also have fewer significant figures. Care is also taken that the number of significant figures is reasonable for the situation posed. In some topics, such as optics, more than three significant figures will be used. Finally, if a number is exact, such as the 2 in the formula, c = 2 π r c = 2 π r , it does not affect the number of significant figures in a calculation.

Approximating Vast Numbers: a Trillion Dollars

The U.S. federal deficit in the 2008 fiscal year was a little greater than $10 trillion. Most of us do not have any concept of how much even one trillion actually is. Suppose that you were given a trillion dollars in $100 bills. If you made 100-bill stacks, like that shown in Figure 1.25 , and used them to evenly cover a football field (between the end zones), make an approximation of how high the money pile would become. (We will use feet/inches rather than meters here because football fields are measured in yards.) One of your friends says 3 in., while another says 10 ft. What do you think?

When you imagine the situation, you probably envision thousands of small stacks of 100 wrapped $100 bills, such as you might see in movies or at a bank. Since this is an easy-to-approximate quantity, let us start there. We can find the volume of a stack of 100 bills, find out how many stacks make up one trillion dollars, and then set this volume equal to the area of the football field multiplied by the unknown height.

• Calculate the volume of a stack of 100 bills. The dimensions of a single bill are approximately 3 in. by 6 in. A stack of 100 of these is about 0.5 in. thick. So the total volume of a stack of 100 bills is volume of stack = length × width × height, volume of stack = 6 in . × 3 in . × 0 .5 in ., volume of stack = 9 in . 3 . volume of stack = length × width × height, volume of stack = 6 in . × 3 in . × 0 .5 in ., volume of stack = 9 in . 3 .

Calculate the number of stacks. Note that a trillion dollars is equal to $ 1 × 10 12 $ 1 × 10 12 , and a stack of one-hundred $ 100 $ 100 bills is equal to $ 10 , 000 , $ 10 , 000 , or $ 1 × 10 4 $ 1 × 10 4 . The number of stacks you will have is

Calculate the area of a football field in square inches. The area of a football field is 100  yd ×  50   yd 100  yd ×  50   yd , which gives 5 , 000  yd 2 5 , 000  yd 2 . Because we are working in inches, we need to convert square yards to square inches

This conversion gives us 6 × 10 6  in . 2 6 × 10 6  in . 2 for the area of the field. (Note that we are using only one significant figure in these calculations.)

• Calculate the total volume of the bills. The volume of all the $100-bill stacks is 9 in . 3  / stack × 10 8  stacks = 9 × 10 8  in . 3 9 in . 3  / stack × 10 8  stacks = 9 × 10 8  in . 3

The height of the money will be about 100 in. high. Converting this value to feet gives

The final approximate value is much higher than the early estimate of 3 in., but the other early estimate of 10 ft (120 in.) was roughly correct. How did the approximation measure up to your first guess? What can this exercise tell you in terms of rough guesstimates versus carefully calculated approximations?

In the example above, the final approximate value is much higher than the first friend’s early estimate of 3 in. However, the other friend’s early estimate of 10 ft. (120 in.) was roughly correct. How did the approximation measure up to your first guess? What can this exercise suggest about the value of rough guesstimates versus carefully calculated approximations?

Graphing in Physics

Most results in science are presented in scientific journal articles using graphs. Graphs present data in a way that is easy to visualize for humans in general, especially someone unfamiliar with what is being studied. They are also useful for presenting large amounts of data or data with complicated trends in an easily-readable way.

One commonly-used graph in physics and other sciences is the line graph , probably because it is the best graph for showing how one quantity changes in response to the other. Let’s build a line graph based on the data in Table 1.5 , which shows the measured distance that a train travels from its station versus time. Our two variables , or things that change along the graph, are time in minutes, and distance from the station, in kilometers. Remember that measured data may not have perfect accuracy.

• Draw the two axes. The horizontal axis, or x -axis, shows the independent variable , which is the variable that is controlled or manipulated. The vertical axis, or y -axis, shows the dependent variable , the non-manipulated variable that changes with (or is dependent on) the value of the independent variable. In the data above, time is the independent variable and should be plotted on the x -axis. Distance from the station is the dependent variable and should be plotted on the y -axis.
• Label each axes on the graph with the name of each variable, followed by the symbol for its units in parentheses. Be sure to leave room so that you can number each axis. In this example, use Time (min) as the label for the x -axis.

Next, you must determine the best scale to use for numbering each axis. Because the time values on the x -axis are taken every 10 minutes, we could easily number the x -axis from 0 to 70 minutes with a tick mark every 10 minutes. Likewise, the y -axis scale should start low enough and continue high enough to include all of the distance from station values. A scale from 0 km to 160 km should suffice, perhaps with a tick mark every 10 km.

In general, you want to pick a scale for both axes that 1) shows all of your data, and 2) makes it easy to identify trends in your data. If you make your scale too large, it will be harder to see how your data change. Likewise, the smaller and more fine you make your scale, the more space you will need to make the graph. The number of significant figures in the axis values should be coarser than the number of significant figures in the measurements.

• Add a title to the top of the graph to state what the graph is describing, such as the y -axis parameter vs. the x -axis parameter. In the graph shown here, the title is train motion . It could also be titled distance of the train from the station vs. time.

Analyzing a Graph Using Its Equation

One way to get a quick snapshot of a dataset is to look at the equation of its trend line . If the graph produces a straight line, the equation of the trend line takes the form

The b in the equation is the y -intercept while the m in the equation is the slope . The y -intercept tells you at what y value the line intersects the y -axis. In the case of the graph above, the y -intercept occurs at 0, at the very beginning of the graph. The y -intercept, therefore, lets you know immediately where on the y -axis the plot line begins.

The m in the equation is the slope. This value describes how much the line on the graph moves up or down on the y -axis along the line’s length. The slope is found using the following equation

In order to solve this equation, you need to pick two points on the line (preferably far apart on the line so the slope you calculate describes the line accurately). The quantities Y 2 and Y 1 represent the y -values from the two points on the line (not data points) that you picked, while X 2 and X 1 represent the two x -values of the those points.

What can the slope value tell you about the graph? The slope of a perfectly horizontal line will equal zero, while the slope of a perfectly vertical line will be undefined because you cannot divide by zero. A positive slope indicates that the line moves up the y -axis as the x -value increases while a negative slope means that the line moves down the y -axis. The more negative or positive the slope is, the steeper the line moves up or down, respectively. The slope of our graph in Figure 1.26 is calculated below based on the two endpoints of the line

Equation of line: y = ( 2.0  km/min ) x + 0 y = ( 2.0  km/min ) x + 0

Because the x axis is time in minutes, we would actually be more likely to use the time t as the independent ( x- axis) variable and write the equation as

The formula y = m x + b y = m x + b only applies to linear relationships , or ones that produce a straight line. Another common type of line in physics is the quadratic relationship , which occurs when one of the variables is squared. One quadratic relationship in physics is the relation between the speed of an object its centripetal acceleration, which is used to determine the force needed to keep an object moving in a circle. Another common relationship in physics is the inverse relationship , in which one variable decreases whenever the other variable increases. An example in physics is Coulomb’s law. As the distance between two charged objects increases, the electrical force between the two charged objects decreases. Inverse proportionality , such the relation between x and y in the equation

for some number k , is one particular kind of inverse relationship. A third commonly-seen relationship is the exponential relationship , in which a change in the independent variable produces a proportional change in the dependent variable. As the value of the dependent variable gets larger, its rate of growth also increases. For example, bacteria often reproduce at an exponential rate when grown under ideal conditions. As each generation passes, there are more and more bacteria to reproduce. As a result, the growth rate of the bacterial population increases every generation ( Figure 1.28 ).

Using Logarithmic Scales in Graphing

Sometimes a variable can have a very large range of values. This presents a problem when you’re trying to figure out the best scale to use for your graph’s axes. One option is to use a logarithmic (log) scale . In a logarithmic scale, the value each mark labels is the previous mark’s value multiplied by some constant. For a log base 10 scale, each mark labels a value that is 10 times the value of the mark before it. Therefore, a base 10 logarithmic scale would be numbered: 0, 10, 100, 1,000, etc. You can see how the logarithmic scale covers a much larger range of values than the corresponding linear scale, in which the marks would label the values 0, 10, 20, 30, and so on.

If you use a logarithmic scale on one axis of the graph and a linear scale on the other axis, you are using a semi-log plot . The Richter scale, which measures the strength of earthquakes, uses a semi-log plot. The degree of ground movement is plotted on a logarithmic scale against the assigned intensity level of the earthquake, which ranges linearly from 1-10 (see Figure 1.29 (a)).

If a graph has both axes in a logarithmic scale, then it is referred to as a log-log plot . The relationship between the wavelength and frequency of electromagnetic radiation such as light is usually shown as a log-log plot ( Figure 1.29 (b)). Log-log plots are also commonly used to describe exponential functions, such as radioactive decay.

Virtual Physics

Graphing lines.

In this simulation you will examine how changing the slope and y -intercept of an equation changes the appearance of a plotted line. Select slope-intercept form and drag the blue circles along the line to change the line’s characteristics. Then, play the line game and see if you can determine the slope or y -intercept of a given line.

How would the following changes affect a line that is neither horizontal nor vertical and has a positive slope?

• increase the slope but keeping the y -intercept constant
• Increasing the slope will cause the line to rotate clockwise around the y -intercept. Increasing the y -intercept will cause the line to move vertically up on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate counter-clockwise around the y -intercept. Increasing the y -intercept will cause the line to move vertically up on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate clockwise around the y -intercept. Increasing the y -intercept will cause the line to move horizontally right on the graph without changing the line’s slope.
• Increasing the slope will cause the line to rotate counter-clockwise around the y -intercept. Increasing the y -intercept will cause the line to move horizontally right on the graph without changing the line’s slope.

Check Your Understanding

• Conversion between units is easier in metric units.
• Comparison of physical quantities is easy in metric units.
• Metric units are more modern than English units.
• Metric units are based on powers of 2.
• Precision states how much repeated measurements generate the same or closely similar results, while accuracy states how close a measurement is to the true value of the measurement.
• Precision states how close a measurement is to the true value of the measurement, while accuracy states how much repeated measurements generate the same or closely similar result.
• Precision and accuracy are the same thing. They state how much repeated measurements generate the same or closely similar results.
• Precision and accuracy are the same thing. They state how close a measurement is to the true value of the measurement.

Copy and paste the link code above.

Related Items