hypothesis based models

The Scientific Method – Hypotheses, Models, Theories, and Laws

The scientific method is defined as the steps scientists follow to create a view of the world that is accurate, reliable, and consistent.  It’s also a way of minimizing how a scientist’s cultural and personal beliefs impact and influence their work.  It attempts to make a person’s perceptions and interpretations of nature and natural phenomena as scientific and neutral as possible.  It minimizes the amount of prejudice and bias a scientist has on the results of an experiment, hypothesis, or theory.

The scientific method can be broken down into four steps:

• Observe and describe the phenomenon (or group of various phenomena).
• Create a hypothesis that explains the phenomena. In physics, this often means creating a mathematical relation or a causal mechanism.
• Use this hypothesis to attempt to predict other related phenomena or the results of another set of observations.
• Test the performance of these predictions using independent experiments.

If the results of these experiments support the hypothesis, then it may become a theory or even a law of nature.  However, if they do not support the hypothesis, then it either has to be changed or completely rejected.  The main benefit of the scientific method is that it has predictive power—a proven theory can be applied to a wide range of phenomena.  Of course, even the most tested theory may be, at some point, proven wrong because new observations may be recorded or experiments done that contradict it.  Theories can never fully be proven, only fully disproven.

• The Steps of the Scientific Method – A basic introduction
• Wikipedia’s Entry for the Scientific Method – It goes into the history of the method
• Definition of the Scientific Method – Also includes a brief history of its use
• Steps of the Scientific Method – More detail about each of the steps

Testing Hypotheses

Testing a hypothesis can lead to one of two things: the hypothesis is confirmed or the hypothesis is rejected, meaning it either has to be changed or a new hypothesis has to be created.  This must happen if the experiments repeatedly and clearly show that their hypothesis is wrong.  It doesn’t matter how elegant or supported a theory is—if it can be disproven once, it can’t be considered a law of nature.  Experimentation is the supreme rule in the scientific method, and if an experiment shows that the hypothesis isn’t true, it trumps all previous experiments that supported it.  These experiments sometimes directly test the theory, while other times they test the theory indirectly via logic and math.  The scientific method requires that all theories have to be testable in some way—those that can’t are not considered scientific theories.

If a theory is disproven, that theory might still be applicable in some ways, but it’s no longer considered a true law of nature.  For example, Newton’s Laws were disproven in cases where the velocity is greater than the speed of light, but they can still be applied to mechanics that use slower velocities.  Other theories that were widely held to be true for years, even centuries, that have been disproven due to new observations include the idea that the earth is the center of our solar system or that the planets orbited the sun in perfect circular orbits rather than the now-proven elliptical orbits.

Of course, a hypothesis or proven theory isn’t always disproven by one single experiment.  This is because experiments may have errors in them, so a hypothesis that looks like it failed once is tested several times by several independent tests.  Things that can cause errors include faulty instruments, misreading measurements or other data, or the bias of the researcher.  Most measurements are given with a degree of error.  Scientists work to make that degree of error as small as possible while still estimating and calculating everything that could cause errors in a test.

• Testing Software Hypotheses – How to apply the scientific method to software testing
• Testing Scientific Ideas – Including a graph of the process
• Research Hypothesis Testing – What is it, and how is it tested?
• What Hypothesis Testing is All About – A different look at testing

Common Mistakes in Applying the Scientific Method

Unfortunately, the scientific method isn’t always applied correctly.  Mistakes do happen, and some of them are actually fairly common.  Because all scientists are human with biases and prejudices, it can be hard to be truly objective in some cases.  It’s important that all results are as untainted by bias as possible, but that doesn’t always happen. Another common mistake is taking something as common sense or deciding that something is so logical that it doesn’t need to be tested.  Scientists have to remember that everything has to be tested before it can be considered a solid hypothesis.

Scientists also have to be willing to look at every piece of data, even those which invalidate the hypothesis.  Some scientists so strongly believe their hypothesis that they try to explain away data that disproves it.  They want to find some reason as to why that data or experiment must be wrong instead of looking at their hypothesis again.  All data has to be considered in the same way, even if it goes against the hypothesis.

Another common issue is forgetting to estimate all possible errors that could arise during testing.  Some data that contradicts the hypothesis has been explained as falling into the range of error, but really, it was a systematic error that the researchers simply didn’t account for.

• Mistakes Young Researchers Make – 15 common errors new scientists may make
• Experimental Error – A look at false positives and false negatives
• Control of Measurement Errors – How to keep errors in measurement to a minimum
• Errors in Scientific Experiments – What they are and how to handle them

Hypotheses, Models, Theories, and Laws

While some people do incorrectly use words like “theory” and “hypotheses” interchangeably, the scientific community has very strict definitions of these terms.

Hypothesis:   A hypothesis is an observation, usually based on a cause and effect.  It is the basic idea that has not been tested.  A hypothesis is just an idea that explains something.  It must go through a number of experiments designed to prove or disprove it.

Model: A hypothesis becomes a model after some testing has been done and it appears to be a valid observation.  Some models are only valid in specific instances, such as when a value falls within a certain range.  A model may also be called a law.

Scientific theory: A model that has been repeatedly tested and confirmed may become a scientific theory.  These theories have been tested by a number of independent researchers around the world using various experiments, and all have supported the theory.  Theories may be disproven, of course, but only after rigorous testing of a new hypothesis that seems to contradict them.

• What is a Hypothesis? – The definition of a hypothesis and its function in the scientific method
• Hypothesis, Theory, and Law – Definitions of each
• 10 Scientific Laws and Theories – Some examples

The scientific method has been used for years to create hypotheses, test them, and develop them into full scientific theories.  While it appears to be a very simple method at first glance, it’s actually one of the most complex ways of testing and evaluating an observation or idea.  It’s different from other types of explanation because it attempts to remove all bias and move forward using systematic experimentation only.  However, like any method, there is room for error, such as bias or mechanical error.  Of course, just like the theories it tests, the scientific method may someday be revised.

BSC Designer is strategy execution software that enhances strategy formulation and execution through KPIs, strategy maps, and dashboards. Our proprietary strategy implementation system guides companies in practical application of strategic planning.

Privacy Overview

• Science, Tech, Math ›
• Chemistry ›

Scientific Hypothesis, Model, Theory, and Law

Understanding the Difference Between Basic Scientific Terms

Hero Images / Getty Images

• Chemical Laws
• Periodic Table
• Projects & Experiments
• Scientific Method
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

Words have precise meanings in science. For example, "theory," "law," and "hypothesis" don't all mean the same thing. Outside of science, you might say something is "just a theory," meaning it's a supposition that may or may not be true. In science, however, a theory is an explanation that generally is accepted to be true. Here's a closer look at these important, commonly misused terms.

A hypothesis is an educated guess, based on observation. It's a prediction of cause and effect. Usually, a hypothesis can be supported or refuted through experimentation or more observation. A hypothesis can be disproven but not proven to be true.

Example: If you see no difference in the cleaning ability of various laundry detergents, you might hypothesize that cleaning effectiveness is not affected by which detergent you use. This hypothesis can be disproven if you observe a stain is removed by one detergent and not another. On the other hand, you cannot prove the hypothesis. Even if you never see a difference in the cleanliness of your clothes after trying 1,000 detergents, there might be one more you haven't tried that could be different.

Scientists often construct models to help explain complex concepts. These can be physical models like a model volcano or atom  or conceptual models like predictive weather algorithms. A model doesn't contain all the details of the real deal, but it should include observations known to be valid.

Example: The  Bohr model shows electrons orbiting the atomic nucleus, much the same way as the way planets revolve around the sun. In reality, the movement of electrons is complicated but the model makes it clear that protons and neutrons form a nucleus and electrons tend to move around outside the nucleus.

A scientific theory summarizes a hypothesis or group of hypotheses that have been supported with repeated testing. A theory is valid as long as there is no evidence to dispute it. Therefore, theories can be disproven. Basically, if evidence accumulates to support a hypothesis, then the hypothesis can become accepted as a good explanation of a phenomenon. One definition of a theory is to say that it's an accepted hypothesis.

Example: It is known that on June 30, 1908, in Tunguska, Siberia, there was an explosion equivalent to the detonation of about 15 million tons of TNT. Many hypotheses have been proposed for what caused the explosion. It was theorized that the explosion was caused by a natural extraterrestrial phenomenon , and was not caused by man. Is this theory a fact? No. The event is a recorded fact. Is this theory, generally accepted to be true, based on evidence to-date? Yes. Can this theory be shown to be false and be discarded? Yes.

A scientific law generalizes a body of observations. At the time it's made, no exceptions have been found to a law. Scientific laws explain things but they do not describe them. One way to tell a law and a theory apart is to ask if the description gives you the means to explain "why." The word "law" is used less and less in science, as many laws are only true under limited circumstances.

Example: Consider Newton's Law of Gravity . Newton could use this law to predict the behavior of a dropped object but he couldn't explain why it happened.

As you can see, there is no "proof" or absolute "truth" in science. The closest we get are facts, which are indisputable observations. Note, however, if you define proof as arriving at a logical conclusion, based on the evidence, then there is "proof" in science. Some work under the definition that to prove something implies it can never be wrong, which is different. If you're asked to define the terms hypothesis, theory, and law, keep in mind the definitions of proof and of these words can vary slightly depending on the scientific discipline. What's important is to realize they don't all mean the same thing and cannot be used interchangeably.

• Scientific Method Lesson Plan
• What Is an Experiment? Definition and Design
• How To Design a Science Fair Experiment
• Chemistry 101 - Introduction & Index of Topics
• What Is the Difference Between Hard and Soft Science?
• What Is a Control Group?
• Henry's Law Definition
• Chemistry Vocabulary Terms
• Hess's Law Definition
• What Does pH Stand For?
• How to Write a Lab Report
• What Is Chemical Engineering?
• Teach Yourself Chemistry Today
• Check Out These Chemistry Career Options Before You Get a Degree
• Here's How to Calculate pH Values
• Setting Up a Home Chemistry Lab

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Models in Science

Models are of central importance in many scientific contexts. The centrality of models such as inflationary models in cosmology, general-circulation models of the global climate, the double-helix model of DNA, evolutionary models in biology, agent-based models in the social sciences, and general-equilibrium models of markets in their respective domains is a case in point (the Other Internet Resources section at the end of this entry contains links to online resources that discuss these models). Scientists spend significant amounts of time building, testing, comparing, and revising models, and much journal space is dedicated to interpreting and discussing the implications of models.

As a result, models have attracted philosophers’ attention and there are now sizable bodies of literature about various aspects of scientific modeling. A tangible result of philosophical engagement with models is a proliferation of model types recognized in the philosophical literature. Probing models , phenomenological models , computational models , developmental models , explanatory models , impoverished models , testing models , idealized models , theoretical models , scale models , heuristic models , caricature models , exploratory models , didactic models , fantasy models , minimal models , toy models , imaginary models , mathematical models , mechanistic models , substitute models , iconic models , formal models , analogue models , and instrumental models are but some of the notions that are used to categorize models. While at first glance this abundance is overwhelming, it can be brought under control by recognizing that these notions pertain to different problems that arise in connection with models. Models raise questions in semantics (how, if at all, do models represent?), ontology (what kind of things are models?), epistemology (how do we learn and explain with models?), and, of course, in other domains within philosophy of science.

1. Semantics: Models and Representation

2.1 physical objects, 2.2 fictional objects and abstract objects, 2.3 set-theoretic structures, 2.4 descriptions and equations, 3.1 learning about models, 3.2 learning about target systems, 3.3 explaining with models, 3.4 understanding with models, 3.5 other cognitive functions, 4.1 models as subsidiaries to theory, 4.2 models as independent from theories, 5.1 models, realism, and laws of nature, 5.2 models and reductionism, other internet resources, related entries.

Many scientific models are representational models: they represent a selected part or aspect of the world, which is the model’s target system. Standard examples are the billiard ball model of a gas, the Bohr model of the atom, the Lotka–Volterra model of predator–prey interaction, the Mundell–Fleming model of an open economy, and the scale model of a bridge.

This raises the question what it means for a model to represent a target system. This problem is rather involved and decomposes into various subproblems. For an in-depth discussion of the issue of representation, see the entry on scientific representation . At this point, rather than addressing the issue of what it means for a model to represent, we focus on a number of different kinds of representation that play important roles in the practice of model-based science, namely scale models, analogical models, idealized models, toy models, minimal models, phenomenological models, exploratory models, and models of data. These categories are not mutually exclusive, and a given model can fall into several categories at once.

Scale models . Some models are down-sized or enlarged copies of their target systems (Black 1962). A typical example is a small wooden car that is put into a wind tunnel to explore the actual car’s aerodynamic properties. The intuition is that a scale model is a naturalistic replica or a truthful mirror image of the target; for this reason, scale models are sometimes also referred to as “true models” (Achinstein 1968: Ch. 7). However, there is no such thing as a perfectly faithful scale model; faithfulness is always restricted to some respects. The wooden scale model of the car provides a faithful portrayal of the car’s shape but not of its material. And even in the respects in which a model is a faithful representation, the relation between model-properties and target-properties is usually not straightforward. When engineers use, say, a 1:100 scale model of a ship to investigate the resistance that an actual ship experiences when moving through the water, they cannot simply measure the resistance the model experiences and then multiply it with the scale. In fact, the resistance faced by the model does not translate into the resistance faced by the actual ship in a straightforward manner (that is, one cannot simply scale the water resistance with the scale of the model: the real ship need not have one hundred times the water resistance of its 1:100 model). The two quantities stand in a complicated nonlinear relation with each other, and the exact form of that relation is often highly nontrivial and emerges as the result of a thoroughgoing study of the situation (Sterrett 2006, forthcoming; Pincock forthcoming).

Analogical models . Standard examples of analogical models include the billiard ball model of a gas, the hydraulic model of an economic system, and the dumb hole model of a black hole. At the most basic level, two things are analogous if there are certain relevant similarities between them. In a classic text, Hesse (1963) distinguishes different types of analogies according to the kinds of similarity relations into which two objects enter. A simple type of analogy is one that is based on shared properties. There is an analogy between the earth and the moon based on the fact that both are large, solid, opaque, spherical bodies that receive heat and light from the sun, revolve around their axes, and gravitate towards other bodies. But sameness of properties is not a necessary condition. An analogy between two objects can also be based on relevant similarities between their properties. In this more liberal sense, we can say that there is an analogy between sound and light because echoes are similar to reflections, loudness to brightness, pitch to color, detectability by the ear to detectability by the eye, and so on.

Analogies can also be based on the sameness or resemblance of relations between parts of two systems rather than on their monadic properties. It is in this sense that the relation of a father to his children is asserted to be analogous to the relation of the state to its citizens. The analogies mentioned so far have been what Hesse calls “material analogies”. We obtain a more formal notion of analogy when we abstract from the concrete features of the systems and only focus on their formal set-up. What the analogue model then shares with its target is not a set of features, but the same pattern of abstract relationships (i.e., the same structure, where structure is understood in a formal sense). This notion of analogy is closely related to what Hesse calls “formal analogy”. Two items are related by formal analogy if they are both interpretations of the same formal calculus. For instance, there is a formal analogy between a swinging pendulum and an oscillating electric circuit because they are both described by the same mathematical equation.

A further important distinction due to Hesse is the one between positive, negative, and neutral analogies. The positive analogy between two items consists in the properties or relations they share (both gas molecules and billiard balls have mass); the negative analogy consists in the properties they do not share (billiard balls are colored, gas molecules are not); the neutral analogy comprises the properties of which it is not known (yet) whether they belong to the positive or the negative analogy (do billiard balls and molecules have the same cross section in scattering processes?). Neutral analogies play an important role in scientific research because they give rise to questions and suggest new hypotheses. For this reason several authors have emphasized the heuristic role that analogies play in theory and model construction, as well as in creative thought (Bailer-Jones and Bailer-Jones 2002; Bailer-Jones 2009: Ch. 3; Hesse 1974; Holyoak and Thagard 1995; Kroes 1989; Psillos 1995; and the essays collected in Helman 1988). See also the entry on analogy and analogical reasoning .

It has also been discussed whether using analogical models can in some cases be confirmatory in a Bayesian sense. Hesse (1974: 208–219) argues that this is possible if the analogy is a material analogy. Bartha (2010, 2013 [2019]) disagrees and argues that analogical models cannot be confirmatory in a Bayesian sense because the information encapsulated in an analogical model is part of the relevant background knowledge, which has the consequence that the posterior probability of a hypothesis about a target system cannot change as a result of observing the analogy. Analogical models can therefore only establish the plausibility of a conclusion in the sense of justifying a non-negligible prior probability assignment (Bartha 2010: §8.5).

More recently, these questions have been discussed in the context of so-called analogue experiments, which promise to provide knowledge about an experimentally inaccessible target system (e.g., a black hole) by manipulating another system, the source system (e.g., a Bose–Einstein condensate). Dardashti, Thébault, and Winsberg (2017) and Dardashti, Hartmann et al. (2019) have argued that, given certain conditions, an analogue simulation of one system by another system can confirm claims about the target system (e.g., that black holes emit Hawking radiation). See Crowther et al. (forthcoming) for a critical discussion, and also the entry on computer simulations in science .

Idealized models . Idealized models are models that involve a deliberate simplification or distortion of something complicated with the objective of making it more tractable or understandable. Frictionless planes, point masses, completely isolated systems, omniscient and fully rational agents, and markets in perfect equilibrium are well-known examples. Idealizations are a crucial means for science to cope with systems that are too difficult to study in their full complexity (Potochnik 2017).

Philosophical debates over idealization have focused on two general kinds of idealizations: so-called Aristotelian and Galilean idealizations. Aristotelian idealization amounts to “stripping away”, in our imagination, all properties from a concrete object that we believe are not relevant to the problem at hand. There is disagreement on how this is done. Jones (2005) and Godfrey-Smith (2009) offer an analysis of abstraction in terms of truth: while an abstraction remains silent about certain features or aspects of the system, it does not say anything false and still offers a true (albeit restricted) description. This allows scientists to focus on a limited set of properties in isolation. An example is a classical-mechanics model of the planetary system, which describes the position of an object as a function of time and disregards all other properties of planets. Cartwright (1989: Ch. 5), Musgrave (1981), who uses the term “negligibility assumptions”, and Mäki (1994), who speaks of the “method of isolation”, allow abstractions to say something false, for instance by neglecting a causally relevant factor.

Galilean idealizations are ones that involve deliberate distortions: physicists build models consisting of point masses moving on frictionless planes; economists assume that agents are omniscient; biologists study isolated populations; and so on. Using simplifications of this sort whenever a situation is too difficult to tackle was characteristic of Galileo’s approach to science. For this reason it is common to refer to ‘distortive’ idealizations of this kind as “Galilean idealizations” (McMullin 1985). An example for such an idealization is a model of motion on an ice rink that assumes the ice to be frictionless, when, in reality, it has low but non-zero friction.

Galilean idealizations are sometimes characterized as controlled idealizations, i.e., as ones that allow for de-idealization by successive removal of the distorting assumptions (McMullin 1985; Weisberg 2007). Thus construed, Galilean idealizations don’t cover all distortive idealizations. Batterman (2002, 2011) and Rice (2015, 2019) discuss distortive idealizations that are ineliminable in that they cannot be removed from the model without dismantling the model altogether.

What does a model involving distortions tell us about reality? Laymon (1991) formulated a theory which understands idealizations as ideal limits: imagine a series of refinements of the actual situation which approach the postulated limit, and then require that the closer the properties of a system come to the ideal limit, the closer its behavior has to come to the behavior of the system at the limit (monotonicity). If this is the case, then scientists can study the system at the limit and carry over conclusions from that system to systems distant from the limit. But these conditions need not always hold. In fact, it can happen that the limiting system does not approach the system at the limit. If this happens, we are faced with a singular limit (Berry 2002). In such cases the system at the limit can exhibit behavior that is different from the behavior of systems distant from the limit. Limits of this kind appear in a number of contexts, most notably in the theory of phase transitions in statistical mechanics. There is, however, no agreement over the correct interpretation of such limits. Batterman (2002, 2011) sees them as indicative of emergent phenomena, while Butterfield (2011a,b) sees them as compatible with reduction (see also the entries on intertheory relations in physics and scientific reduction ).

Galilean and Aristotelian idealizations are not mutually exclusive, and many models exhibit both in that they take into account a narrow set of properties and distort them. Consider again the classical-mechanics model of the planetary system: the model only takes a narrow set of properties into account and distorts them, for instance by describing planets as ideal spheres with a rotation-symmetric mass distribution.

A concept that is closely related to idealization is approximation. In a broad sense, A can be called an approximation of B if A is somehow close to B . This, however, is too broad because it makes room for any likeness to qualify as an approximation. Rueger and Sharp (1998) limit approximations to quantitative closeness, and Portides (2007) frames it as an essentially mathematical concept. On that notion A is an approximation of B iff A is close to B in a specifiable mathematical sense, where the relevant sense of “close” will be given by the context. An example is the approximation of one curve with another one, which can be achieved by expanding a function into a power series and only keeping the first two or three terms. In different situations we approximate an equation with another one by letting a control parameter tend towards zero (Redhead 1980). This raises the question of how approximations are different from idealizations, which can also involve mathematical closeness. Norton (2012) sees the distinction between the two as referential: an approximation is an inexact description of the target while an idealization introduces a secondary system (real or fictitious) which stands for the target system (while being distinct from it). If we say that the period of the pendulum on the wall is roughly two seconds, then this is an approximation; if we reason about the real pendulum by assuming that the pendulum bob is a point mass and that the string is massless (i.e., if we assume that the pendulum is a so-called ideal pendulum), then we use an idealization. Separating idealizations and approximations in this way does not imply that there cannot be interesting relations between the two. For instance, an approximation can be justified by pointing out that it is the mathematical expression of an acceptable idealization (e.g., when we neglect a dissipative term in an equation of motion because we make the idealizing assumption that the system is frictionless).

Toy models . Toy models are extremely simplified and strongly distorted renderings of their targets, and often only represent a small number of causal or explanatory factors (Hartmann 1995; Reutlinger et al. 2018; Nguyen forthcoming). Typical examples are the Lotka–Volterra model in population ecology (Weisberg 2013) and the Schelling model of segregation in the social sciences (Sugden 2000). Toy models usually do not perform well in terms of prediction and empirical adequacy, and they seem to serve other epistemic goals (more on these in Section 3 ). This raises the question whether they should be regarded as representational at all (Luczak 2017).

Some toy models are characterized as “caricatures” (Gibbard and Varian 1978; Batterman and Rice 2014). Caricature models isolate a small number of salient characteristics of a system and distort them into an extreme case. A classic example is Akerlof’s (1970) model of the car market (“the market for lemons”), which explains the difference in price between new and used cars solely in terms of asymmetric information, thereby disregarding all other factors that may influence the prices of cars (see also Sugden 2000). However, it is controversial whether such highly idealized models can still be regarded as informative representations of their target systems. For a discussion of caricature models, in particular in economics, see Reiss (2006).

Minimal models . Minimal models are closely related to toy models in that they are also highly simplified. They are so simplified that some argue that they are non-representational: they lack any similarity, isomorphism, or resemblance relation to the world (Batterman and Rice 2014). It has been argued that many economic models are of this kind (Grüne-Yanoff 2009). Minimal economic models are also unconstrained by natural laws, and do not isolate any real factors ( ibid .). And yet, minimal models help us to learn something about the world in the sense that they function as surrogates for a real system: scientists can study the model to learn something about the target. It is, however, controversial whether minimal models can assist scientists in learning something about the world if they do not represent anything (Fumagalli 2016). Minimal models that purportedly lack any similarity or representation are also used in different parts of physics to explain the macro-scale behavior of various systems whose micro-scale behavior is extremely diverse (Batterman and Rice 2014; Rice 2018, 2019; Shech 2018). Typical examples are the features of phase transitions and the flow of fluids. Proponents of minimal models argue that what provides an explanation of the macro-scale behavior of a system in these cases is not a feature that system and model have in common, but the fact that the system and the model belong to the same universality class (a class of models that exhibit the same limiting behavior even though they show very different behavior at finite scales). It is, however, controversial whether explanations of this kind are possible without reference to at least some common features (Lange 2015; Reutlinger 2017).

Phenomenological models . Phenomenological models have been defined in different, although related, ways. A common definition takes them to be models that only represent observable properties of their targets and refrain from postulating hidden mechanisms and the like (Bokulich 2011). Another approach, due to McMullin (1968), defines phenomenological models as models that are independent of theories. This, however, seems to be too strong. Many phenomenological models, while failing to be derivable from a theory, incorporate principles and laws associated with theories. The liquid-drop model of the atomic nucleus, for instance, portrays the nucleus as a liquid drop and describes it as having several properties (surface tension and charge, among others) originating in different theories (hydrodynamics and electrodynamics, respectively). Certain aspects of these theories—although usually not the full theories—are then used to determine both the static and dynamical properties of the nucleus. Finally, it is tempting to identify phenomenological models with models of a phenomenon . Here, “phenomenon” is an umbrella term covering all relatively stable and general features of the world that are interesting from a scientific point of view. The weakening of sound as a function of the distance to the source, the decay of alpha particles, the chemical reactions that take place when a piece of limestone dissolves in an acid, the growth of a population of rabbits, and the dependence of house prices on the base rate of the Federal Reserve are phenomena in this sense. For further discussion, see Bailer-Jones (2009: Ch. 7), Bogen and Woodward (1988), and the entry on theory and observation in science .

Exploratory models . Exploratory models are models which are not proposed in the first place to learn something about a specific target system or a particular experimentally established phenomenon. Exploratory models function as the starting point of further explorations in which the model is modified and refined. Gelfert (2016) points out that exploratory models can provide proofs-of-principle and suggest how-possibly explanations (2016: Ch. 4). As an example, Gelfert mentions early models in theoretical ecology, such as the Lotka–Volterra model of predator–prey interaction, which mimic the qualitative behavior of speed-up and slow-down in population growth in an environment with limited resources (2016: 80). Such models do not give an accurate account of the behavior of any actual population, but they provide the starting point for the development of more realistic models. Massimi (2019) notes that exploratory models provide modal knowledge. Fisher (2006) sees these models as tools for the examination of the features of a given theory.

Models of data. A model of data (sometimes also “data model”) is a corrected, rectified, regimented, and in many instances idealized version of the data we gain from immediate observation, the so-called raw data (Suppes 1962). Characteristically, one first eliminates errors (e.g., removes points from the record that are due to faulty observation) and then presents the data in a “neat” way, for instance by drawing a smooth curve through a set of points. These two steps are commonly referred to as “data reduction” and “curve fitting”. When we investigate, for instance, the trajectory of a certain planet, we first eliminate points that are fallacious from the observation records and then fit a smooth curve to the remaining ones. Models of data play a crucial role in confirming theories because it is the model of data, and not the often messy and complex raw data, that theories are tested against.

The construction of a model of data can be extremely complicated. It requires sophisticated statistical techniques and raises serious methodological as well as philosophical questions. How do we decide which points on the record need to be removed? And given a clean set of data, what curve do we fit to it? The first question has been dealt with mainly within the context of the philosophy of experiment (see, for instance, Galison 1997 and Staley 2004). At the heart of the latter question lies the so-called curve-fitting problem, which is that the data themselves dictate neither the form of the fitted curve nor what statistical techniques scientists should use to construct a curve. The choice and rationalization of statistical techniques is the subject matter of the philosophy of statistics, and we refer the reader to the entry Philosophy of Statistics and to Bandyopadhyay and Forster (2011) for a discussion of these issues. Further discussions of models of data can be found in Bailer-Jones (2009: Ch. 7), Brewer and Chinn (1994), Harris (2003), Hartmann (1995), Laymon (1982), Mayo (1996, 2018), and Suppes (2007).

The gathering, processing, dissemination, analysis, interpretation, and storage of data raise many important questions beyond the relatively narrow issues pertaining to models of data. Leonelli (2016, 2019) investigates the status of data in science, argues that data should be defined not by their provenance but by their evidential function, and studies how data travel between different contexts.

2. Ontology: What Are Models?

What are models? That is, what kind of object are scientists dealing with when they work with a model? A number of authors have voiced skepticism that this question has a meaningful answer, because models do not belong to a distinctive ontological category and anything can be a model (Callender and Cohen 2006; Giere 2010; Suárez 2004; Swoyer 1991; Teller 2001). Contessa (2010) replies that this is a non sequitur . Even if, from an ontological point of view, anything can be a model and the class of things that are referred to as models contains a heterogeneous collection of different things, it does not follow that it is either impossible or pointless to develop an ontology of models. This is because even if not all models are of a particular ontological kind, one can nevertheless ask to what ontological kinds the things that are de facto used as models belong. There may be several such kinds and each kind can be analyzed in its own right. What sort of objects scientists use as models has important repercussions for how models perform relevant functions such as representation and explanation, and hence this issue cannot be dismissed as “just sociology”.

The objects that commonly serve as models indeed belong to different ontological kinds: physical objects, fictional objects, abstract objects, set-theoretic structures, descriptions, equations, or combinations of some of these, are frequently referred to as models, and some models may fall into yet other classes of things. Following Contessa’s advice, the aim then is to develop an ontology for each of these. Those with an interest in ontology may see this as a goal in its own right. It pays noting, however, that the question has reverberations beyond ontology and bears on how one understands the semantics and the epistemology of models.

Some models are physical objects. Such models are commonly referred to as “material models”. Standard examples of models of this kind are scale models of objects like bridges and ships (see Section 1 ), Watson and Crick’s metal model of DNA (Schaffner 1969), Phillips and Newlyn’s hydraulic model of an economy (Morgan and Boumans 2004), the US Army Corps of Engineers’ model of the San Francisco Bay (Weisberg 2013), Kendrew’s plasticine model of myoglobin (Frigg and Nguyen 2016), and model organisms in the life sciences (Leonelli and Ankeny 2012; Leonelli 2010; Levy and Currie 2015). All these are material objects that serve as models. Material models do not give rise to ontological difficulties over and above the well-known problems in connection with objects that metaphysicians deal with, for instance concerning the nature of properties, the identity of objects, parts and wholes, and so on.

However, many models are not material models. The Bohr model of the atom, a frictionless pendulum, or an isolated population, for instance, are in the scientist’s mind rather than in the laboratory and they do not have to be physically realized and experimented upon to serve as models. These “non-physical” models raise serious ontological questions, and how they are best analyzed is debated controversially. In the remainder of this section we review some of the suggestions that have attracted attention in the recent literature on models.

What has become known as the fiction view of models sees models as akin to the imagined objects of literary fiction—that is, as akin to fictional characters like Sherlock Holmes or fictional places like Middle Earth (Godfrey-Smith 2007). So when Bohr introduced his model of the atom he introduced a fictional object of the same kind as the object Conan Doyle introduced when he invented Sherlock Holmes. This view squares well with scientific practice, where scientists often talk about models as if they were objects and often take themselves to be describing imaginary atoms, populations, or economies. It also squares well with philosophical views that see the construction and manipulation of models as essential aspects of scientific investigation (Morgan 1999), even if models are not material objects, because these practices seem to be directed toward some kind of object.

What philosophical questions does this move solve? Fictional discourse and fictional entities face well-known philosophical questions, and one may well argue that simply likening models to fictions amounts to explaining obscurum per obscurius (for a discussion of these questions, see the entry on fictional entities ). One way to counter this objection and to motivate the fiction view of models is to point to the view’s heuristic power. In this vein Frigg (2010b) identifies five specific issues that an ontology of models has to address and then notes that these issues arise in very similar ways in the discussion about fiction (the issues are the identity conditions, property attribution, the semantics of comparative statements, truth conditions, and the epistemology of imagined objects). Likening models to fiction then has heuristic value because there is a rich literature on fiction that offers a number of solutions to these issues.

Only a small portion of the options available in the extensive literature on fictions have actually been explored in the context of scientific models. Contessa (2010) formulates what he calls the “dualist account”, according to which a model is an abstract object that stands for a possible concrete object. The Rutherford model of the atom, for instance, is an abstract object that acts as a stand-in for one of the possible systems that contain an electron orbiting around a nucleus in a well-defined orbit. Barberousse and Ludwig (2009) and Frigg (2010b) take a different route and develop an account of models as fictions based on Walton’s (1990) pretense theory of fiction. According to this view the sentences of a passage of text introducing a model should be seen as a prop in a game of make-believe, and the model is the product of an act of pretense. This is an antirealist position in that it takes talk of model “objects” to be figures of speech because ultimately there are no model objects—models only live in scientists’ imaginations. Salis (forthcoming) reformulates this view to become what she calls “the new fiction view of models”. The core difference lies in the fact that what is considered as the model are the model descriptions and their content rather than the imaginings that they prescribe. This is a realist view of models, because descriptions exist.

The fiction view is not without critics. Giere (2009), Magnani (2012), Pincock (2012), Portides (2014), and Teller (2009) reject the fiction approach and argue, in different ways, that models should not be regarded as fictions. Weisberg (2013) argues for a middle position which sees fictions as playing a heuristic role but denies that they should be regarded as forming part of a scientific model. The common core of these criticisms is that the fiction view misconstrues the epistemic standing of models. To call something a fiction, so the charge goes, is tantamount to saying that it is false, and it is unjustified to call an entire model a fiction—and thereby claim that it fails to capture how the world is—just because the model involves certain false assumptions or fictional elements. In other words, a representation isn’t automatically counted as fiction just because it has some inaccuracies. Proponents of the fiction view agree with this point but deny that the notion of fiction should be analyzed in terms of falsity. What makes a work a fiction is not its falsity (or some ratio of false to true claims): neither is everything that is said in a novel untrue (Tolstoy’s War and Peace contains many true statements about Napoleon’s Franco-Russian War), nor does every text containing false claims qualify as fiction (false news reports are just that, they are not fictions). The defining feature of a fiction is that readers are supposed to imagine the events and characters described, not that they are false (Frigg 2010a; Salis forthcoming).

Giere (1988) advocated the view that “non-physical” models are abstract entities. However, there is little agreement on the nature of abstract objects, and Hale (1988: 86–87) lists no less than twelve different possible characterizations (for a review of the available options, see the entry on abstract objects ). In recent publications, Thomasson (2020) and Thomson-Jones (2020) develop what they call an “artifactualist view” of models, which is based on Thomasson’s (1999) theory of abstract artifacts. This view agrees with the pretense theory that the content of text that introduces a fictional character or a model should be understood as occurring in pretense, but at the same time insists that in producing such descriptions authors create abstract cultural artifacts that then exist independently of either the author or the readers. Artifactualism agrees with Platonism that abstract objects exist, but insists, contra Platonism, that abstract objects are brought into existence through a creative act and are not eternal. This allows the artifactualist to preserve the advantages of pretense theory while at the same time holding the realist view that fictional characters and models actually exist.

An influential point of view takes models to be set-theoretic structures. This position can be traced back to Suppes (1960) and is now, with slight variants, held by most proponents of the so-called semantic view of theories (for a discussion of this view, see the entry on the structure of scientific theories ). There are differences between the versions of the semantic view, but with the exception of Giere (1988) all versions agree that models are structures of one sort or another (Da Costa and French 2000).

This view of models has been criticized on various grounds. One pervasive criticism is that many types of models that play an important role in science are not structures and cannot be accommodated within the structuralist view of models, which can neither account for how these models are constructed nor for how they work in the context of investigation (Cartwright 1999; Downes 1992; Morrison 1999). Examples for such models are interpretative models and mediating models, discussed later in Section 4.2 . Another charge held against the set-theoretic approach is that set-theoretic structures by themselves cannot be representational models—at least if that requires them to share some structure with the target—because the ascription of a structure to a target system which forms part of the physical world relies on a substantive (non-structural) description of the target, which goes beyond what the structuralist approach can afford (Nguyen and Frigg forthcoming).

A time-honored position has it that a model is a stylized description of a target system. It has been argued that this is what scientists display in papers and textbooks when they present a model (Achinstein 1968; Black 1962). This view has not been subject to explicit criticism. However, some of the criticisms that have been marshaled against the so-called syntactic view of theories equally threaten a linguistic understanding of models (for a discussion of this view, see the entry on the structure of scientific theories ). First, a standard criticism of the syntactic view is that by associating a theory with a particular formulation, the view misconstrues theory identity because any change in the formulation results in a new theory (Suppe 2000). A view that associates models with descriptions would seem to be open to the same criticism. Second, models have different properties than descriptions: the Newtonian model of the solar system consists of orbiting spheres, but it makes no sense to say this about its description. Conversely, descriptions have properties that models do not have: a description can be written in English and consist of 517 words, but the same cannot be said of a model. One way around these difficulties is to associate the model with the content of a description rather than with the description itself. For a discussion of a position on models that builds on the content of a description, see Salis (forthcoming).

A contemporary version of descriptivism is Levy’s (2012, 2015) and Toon’s (2012) so-called direct-representation view. This view shares with the fiction view of models ( Section 2.2 ) the reliance on Walton’s pretense theory, but uses it in a different way. The main difference is that the views discussed earlier see modeling as introducing a vehicle of representation, the model, that is distinct from the target, and they see the problem as elucidating what kind of thing the model is. On the direct-representation view there are no models distinct from the target; there are only model-descriptions and targets, with no models in-between them. Modeling, on this view, consists in providing an imaginative description of real things. A model-description prescribes imaginings about the real system; the ideal pendulum, for instance, prescribes model-users to imagine the real spring as perfectly elastic and the bob as a point mass. This approach avoids the above problems because the identity conditions for models are given by the conditions for games of make-believe (and not by the syntax of a description) and property ascriptions take place in pretense. There are, however, questions about how this account deals with models that have no target (like models of the ether or four-sex populations), and about how models thus understood deal with idealizations. For a discussion of these points, see Frigg and Nguyen (2016), Poznic (2016), and Salis (forthcoming).

A closely related approach sees models as equations. This is a version of the view that models are descriptions, because equations are syntactic items that describe a mathematical structure. The issues that this view faces are similar to the ones we have already encountered: First, one can describe the same situation using different kinds of coordinates and as a result obtain different equations but without thereby also obtaining a different model. Second, the model and the equation have different properties. A pendulum contains a massless string, but the equation describing its motion does not; and an equation may be inhomogeneous, but the system it describes is not. It is an open question whether these issues can be avoided by appeal to a pretense account.

3. Epistemology: The Cognitive Functions of Models

One of the main reasons why models play such an important role in science is that they perform a number of cognitive functions. For example, models are vehicles for learning about the world. Significant parts of scientific investigation are carried out on models rather than on reality itself because by studying a model we can discover features of, and ascertain facts about, the system the model stands for: models allow for “surrogative reasoning” (Swoyer 1991). For instance, we study the nature of the hydrogen atom, the dynamics of a population, or the behavior of a polymer by studying their respective models. This cognitive function of models has been widely acknowledged in the literature, and some even suggest that models give rise to a new style of reasoning, “model-based reasoning”, according to which “inferences are made by means of creating models and manipulating, adapting, and evaluating them” (Nersessian 2010: 12; see also Magnani, Nersessian, and Thagard 1999; Magnani and Nersessian 2002; and Magnani and Casadio 2016).

Learning about a model happens in two places: in the construction of the model and in its manipulation (Morgan 1999). There are no fixed rules or recipes for model building and so the very activity of figuring out what fits together, and how, affords an opportunity to learn about the model. Once the model is built, we do not learn about its properties by looking at it; we have to use and manipulate the model in order to elicit its secrets.

Depending on what kind of model we are dealing with, building and manipulating a model amount to different activities demanding different methodologies. Material models seem to be straightforward because they are used in common experimental contexts (e.g., we put the model of a car in the wind tunnel and measure its air resistance). Hence, as far as learning about the model is concerned, material models do not give rise to questions that go beyond questions concerning experimentation more generally.

Not so with fictional and abstract models. What constraints are there to the construction of fictional and abstract models, and how do we manipulate them? A natural response seems to be that we do this by performing a thought experiment. Different authors (e.g., Brown 1991; Gendler 2000; Norton 1991; Reiss 2003; Sorensen 1992) have explored this line of argument, but they have reached very different and often conflicting conclusions about how thought experiments are performed and what the status of their outcomes is (for details, see the entry on thought experiments ).

An important class of models is computational in nature. For some models it is possible to derive results or solve equations of a mathematical model analytically. But quite often this is not the case. It is at this point that computers have a great impact, because they allow us to solve problems that are otherwise intractable. Hence, computational methods provide us with knowledge about (the consequences of) a model where analytical methods remain silent. Many parts of current research in both the natural and social sciences rely on computer simulations, which help scientists to explore the consequences of models that cannot be investigated otherwise. The formation and development of stars and galaxies, the dynamics of high-energy heavy-ion reactions, the evolution of life, outbreaks of wars, the progression of an economy, moral behavior, and the consequences of decision procedures in an organization are explored with computer simulations, to mention only a few examples.

Computer simulations are also heuristically important. They can suggest new theories, models, and hypotheses, for example, based on a systematic exploration of a model’s parameter space (Hartmann 1996). But computer simulations also bear methodological perils. For example, they may provide misleading results because, due to the discrete nature of the calculations carried out on a digital computer, they only allow for the exploration of a part of the full parameter space, and this subspace need not reflect every important feature of the model. The severity of this problem is somewhat mitigated by the increasing power of modern computers. But the availability of more computational power can also have adverse effects: it may encourage scientists to swiftly come up with increasingly complex but conceptually premature models, involving poorly understood assumptions or mechanisms and too many additional adjustable parameters (for a discussion of a related problem in the social sciences, see Braun and Saam 2015: Ch. 3). This can lead to an increase in empirical adequacy—which may be welcome for certain forecasting tasks—but not necessarily to a better understanding of the underlying mechanisms. As a result, the use of computer simulations can change the weight we assign to the various goals of science. Finally, the availability of computer power may seduce scientists into making calculations that do not have the degree of trustworthiness one would expect them to have. This happens, for instance, when computers are used to propagate probability distributions forward in time, which can turn out to be misleading (see Frigg et al. 2014). So it is important not to be carried away by the means that new powerful computers offer and lose sight of the actual goals of research. For a discussion of further issues in connection with computer simulations, we refer the reader to the entry on computer simulations in science .

Once we have knowledge about the model, this knowledge has to be “translated” into knowledge about the target system. It is at this point that the representational function of models becomes important again: if a model represents, then it can instruct us about reality because (at least some of) the model’s parts or aspects have corresponding parts or aspects in the world. But if learning is connected to representation and if there are different kinds of representations (analogies, idealizations, etc.), then there are also different kinds of learning. If, for instance, we have a model we take to be a realistic depiction, the transfer of knowledge from the model to the target is accomplished in a different manner than when we deal with an analogue, or a model that involves idealizing assumptions. For a discussion of the different ways in which the representational function of models can be exploited to learn about the target, we refer the reader to the entry Scientific Representation .

Some models explain. But how can they fulfill this function given that they typically involve idealizations? Do these models explain despite or because of the idealizations they involve? Does an explanatory use of models presuppose that they represent, or can non-representational models also explain? And what kind of explanation do models provide?

There is a long tradition requesting that the explanans of a scientific explanation must be true. We find this requirement in the deductive-nomological model (Hempel 1965) as well as in the more recent literature. For instance, Strevens (2008: 297) claims that “no causal account of explanation … allows nonveridical models to explain”. For further discussions, see also Colombo et al. (2015).

Authors working in this tradition deny that idealizations make a positive contribution to explanation and explore how models can explain despite being idealized. McMullin (1968, 1985) argues that a causal explanation based on an idealized model leaves out only features which are irrelevant for the respective explanatory task (see also Salmon 1984 and Piccinini and Craver 2011 for a discussion of mechanism sketches). Friedman (1974) argues that a more realistic (and hence less idealized) model explains better on the unification account. The idea is that idealizations can (at least in principle) be de-idealized (for a critical discussion of this claim in the context of the debate about scientific explanations, see Batterman 2002; Bokulich 2011; Morrison 2005, 2009; Jebeile and Kennedy 2015; and Rice 2015). Strevens (2008) argues that an explanatory causal model has to provide an accurate representation of the relevant causal relationships or processes which the model shares with the target system. The idealized assumptions of a model do not make a difference for the phenomenon under consideration and are therefore explanatorily irrelevant. In contrast, both Potochnik (2017) and Rice (2015) argue that models that explain can directly distort many difference-making causes.

According to Woodward’s (2003) theory, models are tools to find out about the causal relations that hold between certain facts or processes, and it is these relations that do the explanatory work. More specifically, explanations provide information about patterns of counterfactual dependence between the explanans and the explanandum which

enable us to see what sort of difference it would have made for the explanandum if the factors cited in the explanans had been different in various possible ways. (Woodward 2003: 11)

Accounts of causal explanation have also led to various claims about how idealized models can provide explanations, exploring to what extent idealization allows for the misrepresentation of irrelevant causal factors by the explanatory model (Elgin and Sober 2002; Strevens 2004, 2008; Potochnik 2007; Weisberg 2007, 2013). However, having the causally relevant features in common with real systems continues to play the essential role in showing how idealized models can be explanatory.

But is it really the truth of the explanans that makes the model explanatory? Other authors pursue a more radical line and argue that false models explain not only despite their falsity, but in fact because of their falsity. Cartwright (1983: 44) maintains that “the truth doesn’t explain much”. In her so-called “simulacrum account of explanation”, she suggests that we explain a phenomenon by constructing a model that fits the phenomenon into the basic framework of a grand theory (1983: Ch. 8). On this account, the model itself is the explanation we seek. This squares well with basic scientific intuitions, but it leaves us with the question of what notion of explanation is at work (see also Elgin and Sober 2002) and of what explanatory function idealizations play in model explanations (Rice 2018, 2019). Wimsatt (2007: Ch. 6) stresses the role of false models as means to arrive at true theories. Batterman and Rice (2014) argue that models explain because the details that characterize specific systems do not matter for the explanation. Bokulich (2008, 2009, 2011, 2012) pursues a similar line of reasoning and sees the explanatory power of models as being closely related to their fictional nature. Bokulich (2009) and Kennedy (2012) present non-representational accounts of model explanation (see also Jebeile and Kennedy 2015). Reiss (2012) and Woody (2004) provide general discussions of the relationship between representation and explanation.

Many authors have pointed out that understanding is one of the central goals of science (see, for instance, de Regt 2017; Elgin 2017; Khalifa 2017; Potochnik 2017). In some cases, we want to understand a certain phenomenon (e.g., why the sky is blue); in other cases, we want to understand a specific scientific theory (e.g., quantum mechanics) that accounts for a phenomenon in question. Sometimes we gain understanding of a phenomenon by understanding the corresponding theory or model. For instance, Maxwell’s theory of electromagnetism helps us understand why the sky is blue. It is, however, controversial whether understanding a phenomenon always presupposes an understanding of the corresponding theory (de Regt 2009: 26).

Although there are many different ways of gaining understanding, models and the activity of scientific modeling are of particular importance here (de Regt et al. 2009; Morrison 2009; Potochnik 2017; Rice 2016). This insight can be traced back at least to Lord Kelvin who, in his famous 1884 Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light , maintained that “the test of ‘Do we or do we not understand a particular subject in physics?’ is ‘Can we make a mechanical model of it?’” (Kelvin 1884 [1987: 111]; see also Bailer-Jones 2009: Ch. 2; and de Regt 2017: Ch. 6).

But why do models play such a crucial role in the understanding of a subject matter? Elgin (2017) argues that this is not despite, but because, of models being literally false. She views false models as “felicitous falsehoods” that occupy center stage in the epistemology of science, and mentions the ideal-gas model in statistical mechanics and the Hardy–Weinberg model in genetics as examples for literally false models that are central to their respective disciplines. Understanding is holistic and it concerns a topic, a discipline, or a subject matter, rather than isolated claims or facts. Gaining understanding of a context means to have

an epistemic commitment to a comprehensive, systematically linked body of information that is grounded in fact, is duly responsive to reasons or evidence, and enables nontrivial inference, argument, and perhaps action regarding the topic the information pertains to (Elgin 2017: 44)

and models can play a crucial role in the pursuit of these epistemic commitments. For a discussion of Elgin’s account of models and understanding, see Baumberger and Brun (2017) and Frigg and Nguyen (forthcoming).

Elgin (2017), Lipton (2009), and Rice (2016) all argue that models can be used to understand independently of their ability to provide an explanation. Other authors, among them Strevens (2008, 2013), argue that understanding presupposes a scientific explanation and that

an individual has scientific understanding of a phenomenon just in case they grasp a correct scientific explanation of that phenomenon. (Strevens 2013: 510; see, however, Sullivan and Khalifa 2019)

On this account, understanding consists in a particular form of epistemic access an individual scientist has to an explanation. For Strevens this aspect is “grasping”, while for de Regt (2017) it is “intelligibility”. It is important to note that both Strevens and de Regt hold that such “subjective” aspects are a worthy topic for investigations in the philosophy of science. This contrasts with the traditional view (see, e.g., Hempel 1965) that delegates them to the realm of psychology. See Friedman (1974), Trout (2002), and Reutlinger et al. (2018) for further discussions of understanding.

Besides the functions already mentioned, it has been emphasized variously that models perform a number of other cognitive functions. Knuuttila (2005, 2011) argues that the epistemic value of models is not limited to their representational function, and develops an account that views models as epistemic artifacts which allow us to gather knowledge in diverse ways. Nersessian (1999, 2010) stresses the role of analogue models in concept-formation and other cognitive processes. Hartmann (1995) and Leplin (1980) discuss models as tools for theory construction and emphasize their heuristic and pedagogical value. Epstein (2008) lists a number of specific functions of models in the social sciences. Peschard (2011) investigates the way in which models may be used to construct other models and generate new target systems. And Isaac (2013) discusses non-explanatory uses of models which do not rely on their representational capacities.

4. Models and Theory

An important question concerns the relation between models and theories. There is a full spectrum of positions ranging from models being subordinate to theories to models being independent of theories.

To discuss the relation between models and theories in science it is helpful to briefly recapitulate the notions of a model and of a theory in logic. A theory is taken to be a (usually deductively closed) set of sentences in a formal language. A model is a structure (in the sense introduced in Section 2.3 ) that makes all sentences of a theory true when its symbols are interpreted as referring to objects, relations, or functions of a structure. The structure is a model of the theory in the sense that it is correctly described by the theory (see Bell and Machover 1977 or Hodges 1997 for details). Logical models are sometimes also referred to as “models of theory” to indicate that they are interpretations of an abstract formal system.

Models in science sometimes carry over from logic the idea of being the interpretation of an abstract calculus (Hesse 1967). This is salient in physics, where general laws—such as Newton’s equation of motion—lie at the heart of a theory. These laws are applied to a particular system—e.g., a pendulum—by choosing a special force function, making assumptions about the mass distribution of the pendulum etc. The resulting model then is an interpretation (or realization) of the general law.

It is important to keep the notions of a logical and a representational model separate (Thomson-Jones 2006): these are distinct concepts. Something can be a logical model without being a representational model, and vice versa . This, however, does not mean that something cannot be a model in both senses at once. In fact, as Hesse (1967) points out, many models in science are both logical and representational models. Newton’s model of planetary motion is a case in point: the model, consisting of two homogeneous perfect spheres located in otherwise empty space that attract each other gravitationally, is simultaneously a logical model (because it makes the axioms of Newtonian mechanics true when they are interpreted as referring to the model) and a representational model (because it represents the real sun and earth).

There are two main conceptions of scientific theories, the so-called syntactic view of theories and the so-called semantic view of theories (see the entry on the structure of scientific theories ). On both conceptions models play a subsidiary role to theories, albeit in very different ways. The syntactic view of theories (see entry section on the syntactic view ) retains the logical notions of a model and a theory. It construes a theory as a set of sentences in an axiomatized logical system, and a model as an alternative interpretation of a certain calculus (Braithwaite 1953; Campbell 1920 [1957]; Nagel 1961; Spector 1965). If, for instance, we take the mathematics used in the kinetic theory of gases and reinterpret the terms of this calculus in a way that makes them refer to billiard balls, the billiard balls are a model of the kinetic theory of gases in the sense that all sentences of the theory come out true. The model is meant to be something that we are familiar with, and it serves the purpose of making an abstract formal calculus more palpable. A given theory can have different models, and which model we choose depends both on our aims and our background knowledge. Proponents of the syntactic view disagree about the importance of models. Carnap and Hempel thought that models only serve a pedagogic or aesthetic purpose and are ultimately dispensable because all relevant information is contained in the theory (Carnap 1938; Hempel 1965; see also Bailer-Jones 1999). Nagel (1961) and Braithwaite (1953), on the other hand, emphasize the heuristic role of models, and Schaffner (1969) submits that theoretical terms get at least part of their meaning from models.

The semantic view of theories (see entry section on the semantic view ) dispenses with sentences in an axiomatized logical system and construes a theory as a family of models. On this view, a theory literally is a class, cluster, or family of models—models are the building blocks of which scientific theories are made up. Different versions of the semantic view work with different notions of a model, but, as noted in Section 2.3 , in the semantic view models are mostly construed as set-theoretic structures. For a discussion of the different options, we refer the reader to the relevant entry in this encyclopedia (linked at the beginning of this paragraph).

In both the syntactic and the semantic view of theories models are seen as subordinate to theory and as playing no role outside the context of a theory. This vision of models has been challenged in a number of ways, with authors pointing out that models enjoy various degrees of freedom from theory and function autonomously in many contexts. Independence can take many forms, and large parts of the literature on models are concerned with investigating various forms of independence.

Models as completely independent of theory . The most radical departure from a theory-centered analysis of models is the realization that there are models that are completely independent from any theory. An example of such a model is the Lotka–Volterra model. The model describes the interaction of two populations: a population of predators and one of prey animals (Weisberg 2013). The model was constructed using only relatively commonsensical assumptions about predators and prey and the mathematics of differential equations. There was no appeal to a theory of predator–prey interactions or a theory of population growth, and the model is independent of theories about its subject matter. If a model is constructed in a domain where no theory is available, then the model is sometimes referred to as a “substitute model” (Groenewold 1961), because the model substitutes a theory.

Models as a means to explore theory . Models can also be used to explore theories (Morgan and Morrison 1999). An obvious way in which this can happen is when a model is a logical model of a theory (see Section 4.1 ). A logical model is a set of objects and properties that make a formal sentence true, and so one can see in the model how the axioms of the theory play out in a particular setting and what kinds of behavior they dictate. But not all models that are used to explore theories are logical models, and models can represent features of theories in other ways. As an example, consider chaos theory. The equations of non-linear systems, such as those describing the three-body problem, have solutions that are too complex to study with paper-and-pencil methods, and even computer simulations are limited in various ways. Abstract considerations about the qualitative behavior of solutions show that there is a mechanism that has been dubbed “stretching and folding” (see the entry Chaos ). To obtain an idea of the complexity of the dynamics exhibiting stretching and folding, Smale proposed to study a simple model of the flow—now known as the “horseshoe map” (Tabor 1989)—which provides important insights into the nature of stretching and folding. Other examples of models of that kind are the Kac ring model that is used to study equilibrium properties of systems in statistical mechanics (Lavis 2008) and Norton’s dome in Newtonian mechanics (Norton 2003).

Models as complements of theories . A theory may be incompletely specified in the sense that it only imposes certain general constraints but remains silent about the details of concrete situations, which are provided by a model (Redhead 1980). A special case of this situation is when a qualitative theory is known and the model introduces quantitative measures (Apostel 1961). Redhead’s example of a theory that is underdetermined in this way is axiomatic quantum field theory, which only imposes certain general constraints on quantum fields but does not provide an account of particular fields. Harré (2004) notes that models can complement theories by providing mechanisms for processes that are left unspecified in the theory even though they are responsible for bringing about the observed phenomena.

Theories may be too complicated to handle. In such cases a model can complement a theory by providing a simplified version of the theoretical scenario that allows for a solution. Quantum chromodynamics, for instance, cannot easily be used to investigate the physics of an atomic nucleus even though it is the relevant fundamental theory. To get around this difficulty, physicists construct tractable phenomenological models (such as the MIT bag model) which effectively describe the relevant degrees of freedom of the system under consideration (Hartmann 1999, 2001). The advantage of these models is that they yield results where theories remain silent. Their drawback is that it is often not clear how to understand the relationship between the model and the theory, as the two are, strictly speaking, contradictory.

Models as preliminary theories . The notion of a model as a substitute for a theory is closely related to the notion of a developmental model . This term was coined by Leplin (1980), who pointed out how useful models were in the development of early quantum theory, and it is now used as an umbrella notion covering cases in which models are some sort of a preliminary exercise to theory.

Also closely related is the notion of a probing model (or “study model”). Models of this kind do not perform a representational function and are not expected to instruct us about anything beyond the model itself. The purpose of these models is to test new theoretical tools that are used later on to build representational models. In field theory, for instance, the so-called φ 4 -model was studied extensively, not because it was believed to represent anything real, but because it served several heuristic functions: the simplicity of the φ 4 -model allowed physicists to “get a feeling” for what quantum field theories are like and to extract some general features that this simple model shared with more complicated ones. Physicists could study complicated techniques such as renormalization in a simple setting, and it was possible to get acquainted with important mechanisms—in this case symmetry-breaking—that could later be used in different contexts (Hartmann 1995). This is true not only for physics. As Wimsatt (1987, 2007) points out, a false model in genetics can perform many useful functions, among them the following: the false model can help answering questions about more realistic models, provide an arena for answering questions about properties of more complex models, “factor out” phenomena that would not otherwise be seen, serve as a limiting case of a more general model (or two false models may define the extremes of a continuum of cases on which the real case is supposed to lie), or lead to the identification of relevant variables and the estimation of their values.

Interpretative models . Cartwright (1983, 1999) argues that models do not only aid the application of theories that are somehow incomplete; she claims that models are also involved whenever a theory with an overarching mathematical structure is applied. The main theories in physics—classical mechanics, electrodynamics, quantum mechanics, and so on—fall into this category. Theories of that kind are formulated in terms of abstract concepts that need to be concretized for the theory to provide a description of the target system, and concretizing the relevant concepts, idealized objects and processes are introduced. For instance, when applying classical mechanics, the abstract concept of force has to be replaced with a concrete force such as gravity. To obtain tractable equations, this procedure has to be applied to a simplified scenario, for instance that of two perfectly spherical and homogeneous planets in otherwise empty space, rather than to reality in its full complexity. The result is an interpretative model , which grounds the application of mathematical theories to real-world targets. Such models are independent from theory in that the theory does not determine their form, and yet they are necessary for the application of the theory to a concrete problem.

Models as mediators . The relation between models and theories can be complicated and disorderly. The contributors to a programmatic collection of essays edited by Morgan and Morrison (1999) rally around the idea that models are instruments that mediate between theories and the world. Models are “autonomous agents” in that they are independent from both theories and their target systems, and it is this independence that allows them to mediate between the two. Theories do not provide us with algorithms for the construction of a model; they are not “vending machines” into which one can insert a problem and a model pops out (Cartwright 1999). The construction of a model often requires detailed knowledge about materials, approximation schemes, and the setup, and these are not provided by the corresponding theory. Furthermore, the inner workings of a model are often driven by a number of different theories working cooperatively. In contemporary climate modeling, for instance, elements of different theories—among them fluid dynamics, thermodynamics, electromagnetism—are put to work cooperatively. What delivers the results is not the stringent application of one theory, but the voices of different theories when put to use in chorus with each other in one model.

In complex cases like the study of a laser system or the global climate, models and theories can get so entangled that it becomes unclear where a line between the two should be drawn: where does the model end and the theory begin? This is not only a problem for philosophical analysis; it also arises in scientific practice. Bailer-Jones (2002) interviewed a group of physicists about their understanding of models and their relation to theories, and reports widely diverging views: (i) there is no substantive difference between model and theory; (ii) models become theories when their degree of confirmation increases; (iii) models contain simplifications and omissions, while theories are accurate and complete; (iv) theories are more general than models, and modeling is about applying general theories to specific cases. The first suggestion seems to be too radical to do justice to many aspects of practice, where a distinction between models and theories is clearly made. The second view is in line with common parlance, where the terms “model” and “theory” are sometimes used to express someone’s attitude towards a particular hypothesis. The phrase “it’s just a model” indicates that the hypothesis at stake is asserted only tentatively or is even known to be false, while something is awarded the label “theory” if it has acquired some degree of general acceptance. However, this use of “model” is different from the uses we have seen in Sections 1 to 3 and is therefore of no use if we aim to understand the relation between scientific models and theories (and, incidentally, one can equally dismiss speculative claims as being “just a theory”). The third proposal is correct in associating models with idealizations and simplifications, but it overshoots by restricting this to models; in fact, also theories can contain idealizations and simplifications. The fourth view seems closely aligned with interpretative models and the idea that models are mediators, but being more general is a gradual notion and hence does not provide a clear-cut criterion to distinguish between theories and models.

5. Models and Other Debates in the Philosophy of Science

The debate over scientific models has important repercussions for other issues in the philosophy of science (for a historical account of the philosophical discussion about models, see Bailer-Jones 1999). Traditionally, the debates over, say, scientific realism, reductionism, and laws of nature were couched in terms of theories, because theories were seen as the main carriers of scientific knowledge. Once models are acknowledged as occupying an important place in the edifice of science, these issues have to be reconsidered with a focus on models. The question is whether, and if so how, discussions of these issues change when we shift focus from theories to models. Up to now, no comprehensive model-based account of any of these issues has emerged, but models have left important traces in the discussions of these topics.

As we have seen in Section 1 , models typically provide a distorted representation of their targets. If one sees science as primarily model-based, this could be taken to suggest an antirealist interpretation of science. Realists, however, deny that the presence of idealizations in models renders a realist approach to science impossible and point out that a good model, while not literally true, is usually at least approximately true, and/or that it can be improved by de-idealization (Laymon 1985; McMullin 1985; Nowak 1979; Brzezinski and Nowak 1992).

Apart from the usual worries about the elusiveness of the notion of approximate truth (for a discussion, see the entry on truthlikeness ), antirealists have taken issue with this reply for two (related) reasons. First, as Cartwright (1989) points out, there is no reason to assume that one can always improve a model by adding de-idealizing corrections. Second, it seems that de-idealization is not in accordance with scientific practice because it is unusual that scientists invest work in repeatedly de-idealizing an existing model. Rather, they shift to a different modeling framework once the adjustments to be made get too involved (Hartmann 1998). The various models of the atomic nucleus are a case in point: once it was realized that shell effects are important to understand various subatomic phenomena, the (collective) liquid-drop model was put aside and the (single-particle) shell model was developed to account for the corresponding findings. A further difficulty with de-idealization is that most idealizations are not “controlled”. For example, it is not clear in what way one could de-idealize the MIT bag model to eventually arrive at quantum chromodynamics, the supposedly correct underlying theory.

A further antirealist argument, the “incompatible-models argument”, takes as its starting point the observation that scientists often successfully use several incompatible models of one and the same target system for predictive purposes (Morrison 2000). These models seemingly contradict each other, as they ascribe different properties to the same target system. In nuclear physics, for instance, the liquid-drop model explores the analogy of the atomic nucleus with a (charged) fluid drop, while the shell model describes nuclear properties in terms of the properties of protons and neutrons, the constituents of an atomic nucleus. This practice appears to cause a problem for scientific realism: Realists typically hold that there is a close connection between the predictive success of a theory and its being at least approximately true. But if several models of the same system are predictively successful and if these models are mutually inconsistent, then it is difficult to maintain that they are all approximately true.

Realists can react to this argument in various ways. First, they can challenge the claim that the models in question are indeed predictively successful. If the models are not good predictors, then the argument is blocked. Second, they can defend a version of “perspectival realism” (Giere 2006; Massimi 2017; Rueger 2005). Proponents of this position (which is sometimes also called “perspectivism”) situate it somewhere between “standard” scientific realism and antirealism, and where exactly the right middle position lies is the subject matter of active debate (Massimi 2018a,b; Saatsi 2016; Teller 2018; and the contributions to Massimi and McCoy 2019). Third, realists can deny that there is a problem in the first place, because scientific models, which are always idealized and therefore strictly speaking false, are just the wrong vehicle to make a point about realism (which should be discussed in terms of theories).

A particular focal point of the realism debate are laws of nature, where the questions arise what laws are and whether they are truthfully reflected in our scientific representations. According to the two currently dominant accounts, the best-systems approach and the necessitarian approach, laws of nature are understood to be universal in scope, meaning that they apply to everything that there is in the world (for discussion of laws, see the entry on laws of nature ). This take on laws does not seem to sit well with a view that places models at the center of scientific research. What role do general laws play in science if it is models that represent what is happening in the world? And how are models and laws related?

One possible response to these questions is to argue that laws of nature govern entities and processes in a model rather than in the world. Fundamental laws, on this approach, do not state facts about the world but hold true of entities and processes in the model. This view has been advocated in different variants: Cartwright (1983) argues that all laws are ceteris paribus laws. Cartwright (1999) makes use of “capacities” (which she considers to be prior to laws) and introduces the notion of a “nomological machine”. This is

a fixed (enough) arrangement of components, or factors, with stable (enough) capacities that in the right sort of stable (enough) environment will, with repeated operation, give rise to the kind of regular behavior that we represent in our scientific laws. (1999: 50; see also the entry on ceteris paribus laws )

Giere (1999) argues that the laws of a theory are better thought of, not as encoding general truths about the world, but rather as open-ended statements that can be filled in various ways in the process of building more specific scientific models. Similar positions have also been defended by Teller (2001) and van Fraassen (1989).

The multiple-models problem mentioned in Section 5.1 also raises the question of how different models are related. Evidently, multiple models for the same target system do not generally stand in a deductive relationship, as they often contradict each other. Some (Cartwright 1999; Hacking 1983) have suggested a picture of science according to which there are no systematic relations that hold between different models. Some models are tied together because they represent the same target system, but this does not imply that they enter into any further relationships (deductive or otherwise). We are confronted with a patchwork of models, all of which hold ceteris paribus in their specific domains of applicability.

Some argue that this picture is at least partially incorrect because there are various interesting relations that hold between different models or theories. These relations range from thoroughgoing reductive relations (Scheibe 1997, 1999, 2001: esp. Chs. V.23 and V.24) and controlled approximations over singular limit relations (Batterman 2001 [2016]) to structural relations (Gähde 1997) and rather loose relations called “stories” (Hartmann 1999; see also Bokulich 2003; Teller 2002; and the essays collected in Part III of Hartmann et al. 2008). These suggestions have been made on the basis of case studies, and it remains to be seen whether a more general account of these relations can be given and whether a deeper justification for them can be provided, for instance, within a Bayesian framework (first steps towards a Bayesian understanding of reductive relations can be found in Dizadji-Bahmani et al. 2011; Liefke and Hartmann 2018; and Tešić 2019).

Models also figure in the debate about reduction and emergence in physics. Here, some authors argue that the modern approach to renormalization challenges Nagel’s (1961) model of reduction or the broader doctrine of reductions (for a critical discussion, see, for instance, Batterman 2002, 2010, 2011; Morrison 2012; and Saatsi and Reutlinger 2018). Dizadji-Bahmani et al. (2010) provide a defense of the Nagel–Schaffner model of reduction, and Butterfield (2011a,b, 2014) argues that renormalization is consistent with Nagelian reduction. Palacios (2019) shows that phase transitions are compatible with reductionism, and Hartmann (2001) argues that the effective-field-theories research program is consistent with reductionism (see also Bain 2013 and Franklin forthcoming). Rosaler (2015) argues for a “local” form of reduction which sees the fundamental relation of reduction holding between models, not theories, which is, however, compatible with the Nagel–Schaffner model of reduction. See also the entries on intertheory relations in physics and scientific reduction .

In the social sciences, agent-based models (ABMs) are increasingly used (Klein et al. 2018). These models show how surprisingly complex behavioral patterns at the macro-scale can emerge from a small number of simple behavioral rules for the individual agents and their interactions. This raises questions similar to the questions mentioned above about reduction and emergence in physics, but so far one only finds scattered remarks about reduction in the literature. See Weisberg and Muldoon (2009) and Zollman (2007) for the application of ABMs to the epistemology and the social structure of science, and Colyvan (2013) for a discussion of methodological questions raised by normative models in general.

• Achinstein, Peter, 1968, Concepts of Science: A Philosophical Analysis , Baltimore, MD: Johns Hopkins Press.
• Akerlof, George A., 1970, “The Market for ‘Lemons’: Quality Uncertainty and the Market Mechanism”, The Quarterly Journal of Economics , 84(3): 488–500. doi:10.2307/1879431
• Apostel, Leo, 1961, “Towards the Formal Study of Models in the Non-Formal Sciences”, in Freudenthal 1961: 1–37. doi:10.1007/978-94-010-3667-2_1
• Bailer-Jones, Daniela M., 1999, “Tracing the Development of Models in the Philosophy of Science”, in Magnani, Nersessian, and Thagard 1999: 23–40. doi:10.1007/978-1-4615-4813-3_2
• –––, 2002, “Scientists’ Thoughts on Scientific Models”, Perspectives on Science , 10(3): 275–301. doi:10.1162/106361402321899069
• –––, 2009, Scientific Models in Philosophy of Science , Pittsburgh, PA: University of Pittsburgh Press.
• Bailer-Jones, Daniela M. and Coryn A. L. Bailer-Jones, 2002, “Modeling Data: Analogies in Neural Networks, Simulated Annealing and Genetic Algorithms”, in Magnani and Nersessian 2002: 147–165. doi:10.1007/978-1-4615-0605-8_9
• Bain, Jonathan, 2013, “Emergence in Effective Field Theories”, European Journal for Philosophy of Science , 3(3): 257–273. doi:10.1007/s13194-013-0067-0
• Bandyopadhyay, Prasanta S. and Malcolm R. Forster (eds.), 2011, Philosophy of Statistics (Handbook of the Philosophy of Science 7), Amsterdam: Elsevier.
• Barberousse, Anouk and Pascal Ludwig, 2009, “Fictions and Models”, in Suárez 2009: 56–75.
• Bartha, Paul, 2010, By Parallel Reasoning: The Construction and Evaluation of Analogical Arguments , New York: Oxford University Press. doi:10.1093/acprof:oso/9780195325539.001.0001
• –––, 2013 [2019], “Analogy and Analogical Reasoning”, in Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy (Spring 2019 Edition). URL = < https://plato.stanford.edu/archives/spr2019/entries/reasoning-analogy/ >
• Batterman, Robert W., 2002, The Devil in the Details: Asymptotic Reasoning in Explanation, Reduction, and Emergence , Oxford: Oxford University Press. doi:10.1093/0195146476.001.0001
• –––, 2001 [2016], “Intertheory Relations in Physics”, in Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy (Fall 2016 Edition). URL = < https://plato.stanford.edu/archives/fall2016/entries/physics-interrelate >
• –––, 2010, “Reduction and Renormalization”, in Gerhard Ernst and Andreas Hüttemann (eds.), Time, Chance and Reduction: Philosophical Aspects of Statistical Mechanics , Cambridge: Cambridge University Press, pp. 159–179.
• –––, 2011, “Emergence, Singularities, and Symmetry Breaking”, Foundations of Physics , 41(6): 1031–1050. doi:10.1007/s10701-010-9493-4
• Batterman, Robert W. and Collin C. Rice, 2014, “Minimal Model Explanations”, Philosophy of Science , 81(3): 349–376. doi:10.1086/676677
• Baumberger, Christoph and Georg Brun, 2017, “Dimensions of Objectual Understanding”, in Stephen R. Grimm, Christoph Baumberger, and Sabine Ammon (eds.), Explaining Understanding: New Perspectives from Epistemology and Philosophy of Science , New York: Routledge, pp. 165–189.
• Bell, John and Moshé Machover, 1977, A Course in Mathematical Logic , Amsterdam: North-Holland.
• Berry, Michael, 2002, “Singular Limits”, Physics Today , 55(5): 10–11. doi:10.1063/1.1485555
• Black, Max, 1962, Models and Metaphors: Studies in Language and Philosophy , Ithaca, NY: Cornell University Press.
• Bogen, James and James Woodward, 1988, “Saving the Phenomena”, The Philosophical Review , 97(3): 303–352. doi:10.2307/2185445
• Bokulich, Alisa, 2003, “Horizontal Models: From Bakers to Cats”, Philosophy of Science , 70(3): 609–627. doi:10.1086/376927
• –––, 2008, Reexamining the Quantum–Classical Relation: Beyond Reductionism and Pluralism , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511751813
• –––, 2009, “Explanatory Fictions”, in Suárez 2009: 91–109.
• –––, 2011, “How Scientific Models Can Explain”, Synthese , 180(1): 33–45. doi:10.1007/s11229-009-9565-1
• –––, 2012, “Distinguishing Explanatory from Nonexplanatory Fictions”, Philosophy of Science , 79(5): 725–737. doi:10.1086/667991
• Braithwaite, Richard, 1953, Scientific Explanation , Cambridge: Cambridge University Press.
• Braun, Norman and Nicole J. Saam (eds.), 2015, Handbuch Modellbildung und Simulation in den Sozialwissenschaften , Wiesbaden: Springer Fachmedien. doi:10.1007/978-3-658-01164-2
• Brewer, William F. and Clark A. Chinn, 1994, “Scientists’ Responses to Anomalous Data: Evidence from Psychology, History, and Philosophy of Science”, in PSA 1994: Proceedings of the 1994 Biennial Meeting of the Philosophy of Science Association , Vol. 1, pp. 304–313. doi:10.1086/psaprocbienmeetp.1994.1.193035
• Brown, James, 1991, The Laboratory of the Mind: Thought Experiments in the Natural Sciences , London: Routledge.
• Brzezinski, Jerzy and Leszek Nowak (eds.), 1992, Idealization III: Approximation and Truth , Amsterdam: Rodopi.
• Butterfield, Jeremy, 2011a, “Emergence, Reduction and Supervenience: A Varied Landscape”, Foundations of Physics , 41(6): 920–959. doi:10.1007/s10701-011-9549-0
• –––, 2011b, “Less Is Different: Emergence and Reduction Reconciled”, Foundations of Physics , 41(6): 1065–1135. doi:10.1007/s10701-010-9516-1
• –––, 2014, “Reduction, Emergence, and Renormalization”, Journal of Philosophy , 111(1): 5–49. doi:10.5840/jphil201411111
• Callender, Craig and Jonathan Cohen, 2006, “There Is No Special Problem about Scientific Representation”, Theoria , 55(1): 67–85.
• Campbell, Norman, 1920 [1957], Physics: The Elements , Cambridge: Cambridge University Press. Reprinted as Foundations of Science , New York: Dover, 1957.
• Carnap, Rudolf, 1938, “Foundations of Logic and Mathematics”, in Otto Neurath, Charles Morris, and Rudolf Carnap (eds.), International Encyclopaedia of Unified Science , Volume 1, Chicago, IL: University of Chicago Press, pp. 139–213.
• Cartwright, Nancy, 1983, How the Laws of Physics Lie , Oxford: Oxford University Press. doi:10.1093/0198247044.001.0001
• –––, 1989, Nature’s Capacities and Their Measurement , Oxford: Oxford University Press. doi:10.1093/0198235070.001.0001
• –––, 1999, The Dappled World: A Study of the Boundaries of Science , Cambridge: Cambridge University Press. doi:10.1017/CBO9781139167093
• Colombo, Matteo, Stephan Hartmann, and Robert van Iersel, 2015, “Models, Mechanisms, and Coherence”, The British Journal for the Philosophy of Science , 66(1): 181–212. doi:10.1093/bjps/axt043
• Colyvan, Mark, 2013, “Idealisations in Normative Models”, Synthese , 190(8): 1337–1350. doi:10.1007/s11229-012-0166-z
• Contessa, Gabriele, 2010, “Scientific Models and Fictional Objects”, Synthese , 172(2): 215–229. doi:10.1007/s11229-009-9503-2
• Crowther, Karen, Niels S. Linnemann, and Christian Wüthrich, forthcoming, “What We Cannot Learn from Analogue Experiments”, Synthese , first online: 4 May 2019. doi:10.1007/s11229-019-02190-0
• Da Costa, Newton and Steven French, 2000, “Models, Theories, and Structures: Thirty Years On”, Philosophy of Science , 67(supplement): S116–S127. doi:10.1086/392813
• Dardashti, Radin, Stephan Hartmann, Karim Thébault, and Eric Winsberg, 2019, “Hawking Radiation and Analogue Experiments: A Bayesian Analysis”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 67: 1–11. doi:10.1016/j.shpsb.2019.04.004
• Dardashti, Radin, Karim P. Y. Thébault, and Eric Winsberg, 2017, “Confirmation via Analogue Simulation: What Dumb Holes Could Tell Us about Gravity”, The British Journal for the Philosophy of Science , 68(1): 55–89. doi:10.1093/bjps/axv010
• de Regt, Henk, 2009, “Understanding and Scientific Explanation”, in de Regt, Leonelli, and Eigner 2009: 21–42.
• –––, 2017, Understanding Scientific Understanding , Oxford: Oxford University Press. doi:10.1093/oso/9780190652913.001.0001
• de Regt, Henk, Sabina Leonelli, and Kai Eigner (eds.), 2009, Scientific Understanding: Philosophical Perspectives , Pittsburgh, PA: University of Pittsburgh Press.
• Dizadji-Bahmani, Foad, Roman Frigg, and Stephan Hartmann, 2010, “Who’s Afraid of Nagelian Reduction?”, Erkenntnis , 73(3): 393–412. doi:10.1007/s10670-010-9239-x
• –––, 2011, “Confirmation and Reduction: A Bayesian Account”, Synthese , 179(2): 321–338. doi:10.1007/s11229-010-9775-6
• Downes, Stephen M., 1992, “The Importance of Models in Theorizing: A Deflationary Semantic View”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1992(1): 142–153. doi:10.1086/psaprocbienmeetp.1992.1.192750
• Elgin, Catherine Z., 2010, “Telling Instances”, in Roman Frigg and Matthew Hunter (eds.), Beyond Mimesis and Convention (Boston Studies in the Philosophy of Science 262), Dordrecht: Springer Netherlands, pp. 1–17. doi:10.1007/978-90-481-3851-7_1
• –––, 2017, True Enough . Cambridge, MA, and London: MIT Press.
• Elgin, Mehmet and Elliott Sober, 2002, “Cartwright on Explanation and Idealization”, Erkenntnis , 57(3): 441–450. doi:10.1023/A:1021502932490
• Epstein, Joshua M., 2008, “Why Model?”, Journal of Artificial Societies and Social Simulation , 11(4): 12. [ Epstein 2008 available online ]
• Fisher, Grant, 2006, “The Autonomy of Models and Explanation: Anomalous Molecular Rearrangements in Early Twentieth-Century Physical Organic Chemistry”, Studies in History and Philosophy of Science Part A , 37(4): 562–584. doi:10.1016/j.shpsa.2006.09.009
• Franklin, Alexander, forthcoming, “Whence the Effectiveness of Effective Field Theories?”, The British Journal for the Philosophy of Science , first online: 3 August 2018. doi:10.1093/bjps/axy050
• Freudenthal, Hans (ed.), 1961, The Concept and the Role of the Model in Mathematics and Natural and Social Sciences , Dordrecht: Reidel. doi:10.1007/978-94-010-3667-2
• Friedman, Michael, 1974, “Explanation and Scientific Understanding”, Journal of Philosophy , 71(1): 5–19. doi:10.2307/2024924
• Frigg, Roman, 2010a, “Fiction in Science”, in John Woods (ed.), Fictions and Models: New Essays , Munich: Philosophia Verlag, pp. 247–287.
• –––, 2010b, “Models and Fiction”, Synthese , 172(2): 251–268. doi:10.1007/s11229-009-9505-0
• Frigg, Roman, Seamus Bradley, Hailiang Du, and Leonard A. Smith, 2014, “Laplace’s Demon and the Adventures of His Apprentices”, Philosophy of Science , 81(1): 31–59. doi:10.1086/674416
• Frigg, Roman and James Nguyen, 2016, “The Fiction View of Models Reloaded”, The Monist , 99(3): 225–242. doi:10.1093/monist/onw002 [ Frigg and Nguyen 2016 available online ]
• –––, forthcoming, “Mirrors without Warnings”, Synthese , first online: 21 May 2019. doi:10.1007/s11229-019-02222-9
• Fumagalli, Roberto, 2016, “Why We Cannot Learn from Minimal Models”, Erkenntnis , 81(3): 433–455. doi:10.1007/s10670-015-9749-7
• Gähde, Ulrich, 1997, “Anomalies and the Revision of Theory-Elements: Notes on the Advance of Mercury’s Perihelion”, in Maria Luisa Dalla Chiara, Kees Doets, Daniele Mundici, and Johan van Benthem (eds.), Structures and Norms in Science (Synthese Library 260), Dordrecht: Springer Netherlands, pp. 89–104. doi:10.1007/978-94-017-0538-7_6
• Galison, Peter, 1997, Image and Logic: A Material Culture of Microphysics , Chicago, IL: University of Chicago Press.
• Gelfert, Axel, 2016, How to Do Science with Models: A Philosophical Primer (Springer Briefs in Philosophy), Cham: Springer International Publishing. doi:10.1007/978-3-319-27954-1
• Gendler, Tamar Szabó, 2000, Thought Experiment: On the Powers and Limits of Imaginary Cases , New York and London: Garland.
• Gibbard, Allan and Hal R. Varian, 1978, “Economic Models”, The Journal of Philosophy , 75(11): 664–677. doi:10.5840/jphil1978751111
• Giere, Ronald N., 1988, Explaining Science: A Cognitive Approach , Chicago, IL: University of Chicago Press.
• –––, 1999, Science Without Laws , Chicago, IL: University of Chicago Press.
• –––, 2006, Scientific Perspectivism , Chicago, IL: University of Chicago Press.
• –––, 2009, “Why Scientific Models Should Not be Regarded as Works of Fiction”, in Suárez 2009: 248–258.
• –––, 2010, “An Agent-Based Conception of Models and Scientific Representation”, Synthese , 172(2): 269–281. doi:10.1007/s11229-009-9506-z
• Godfrey-Smith, Peter, 2007, “The Strategy of Model-Based Science”, Biology & Philosophy , 21(5): 725–740. doi:10.1007/s10539-006-9054-6
• –––, 2009, “Abstractions, Idealizations, and Evolutionary Biology”, in Anouk Barberousse, Michel Morange, and Thomas Pradeu (eds.), Mapping the Future of Biology: Evolving Concepts and Theories (Boston Studies in the Philosophy of Science 266), Dordrecht: Springer Netherlands, pp. 47–56. doi:10.1007/978-1-4020-9636-5_4
• Groenewold, H. J., 1961, “The Model in Physics”, in Freudenthal 1961: 98–103. doi:10.1007/978-94-010-3667-2_9
• Grüne-Yanoff, Till, 2009, “Learning from Minimal Economic Models”, Erkenntnis , 70(1): 81–99. doi:10.1007/s10670-008-9138-6
• Hacking, Ian, 1983, Representing and Intervening: Introductory Topics in the Philosophy of Natural Science , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511814563
• Hale, Susan C., 1988, “Spacetime and the Abstract/Concrete Distinction”, Philosophical Studies , 53(1): 85–102. doi:10.1007/BF00355677
• Harré, Rom, 2004, Modeling: Gateway to the Unknown (Studies in Multidisciplinarity 1), ed. by Daniel Rothbart, Amsterdam etc.: Elsevier.
• Harris, Todd, 2003, “Data Models and the Acquisition and Manipulation of Data”, Philosophy of Science , 70(5): 1508–1517. doi:10.1086/377426
• Hartmann, Stephan, 1995, “Models as a Tool for Theory Construction: Some Strategies of Preliminary Physics”, in Herfel et al. 1995: 49–67.
• –––, 1996, “The World as a Process: Simulations in the Natural and Social Sciences”, in Hegselmann, Mueller, and Troitzsch 1996: 77–100. doi:10.1007/978-94-015-8686-3_5
• –––, 1998, “Idealization in Quantum Field Theory”, in Shanks 1998: 99–122.
• –––, 1999, “Models and Stories in Hadron Physics”, in Morgan and Morrison 1999: 326–346. doi:10.1017/CBO9780511660108.012
• –––, 2001, “Effective Field Theories, Reductionism and Scientific Explanation”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 32(2): 267–304. doi:10.1016/S1355-2198(01)00005-3
• Hartmann, Stephan, Carl Hoefer, and Luc Bovens (eds.), 2008, Nancy Cartwright’s Philosophy of Science (Routledge Studies in the Philosophy of Science), New York: Routledge.
• Hegselmann, Rainer, Ulrich Mueller, and Klaus G. Troitzsch (eds.), 1996, Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View (Theory and Decision Library 23), Dordrecht: Springer Netherlands. doi:10.1007/978-94-015-8686-3
• Helman, David H. (ed.), 1988, Analogical Reasoning: Perspectives of Artificial Intelligence, Cognitive Science, and Philosophy (Synthese Library 197), Dordrecht: Springer Netherlands. doi:10.1007/978-94-015-7811-0
• Hempel, Carl G., 1965, Aspects of Scientific Explanation and Other Essays in the Philosophy of Science , New York: Free Press.
• Herfel, William, Wladiysław Krajewski, Ilkka Niiniluoto, and Ryszard Wojcicki (eds.), 1995, Theories and Models in Scientific Process (Poznań Studies in the Philosophy of Science and the Humanities 44), Amsterdam: Rodopi.
• Hesse, Mary, 1963, Models and Analogies in Science , London: Sheed and Ward.
• –––, 1967, “Models and Analogy in Science”, in Paul Edwards (ed.), Encyclopedia of Philosophy , New York: Macmillan, pp. 354–359.
• –––, 1974, The Structure of Scientific Inference , London: Macmillan.
• Hodges, Wilfrid, 1997, A Shorter Model Theory , Cambridge: Cambridge University Press.
• Holyoak, Keith and Paul Thagard, 1995, Mental Leaps: Analogy in Creative Thought , Cambridge, MA: MIT Press.
• Horowitz, Tamara and Gerald J. Massey (eds.), 1991, Thought Experiments in Science and Philosophy , Lanham, MD: Rowman & Littlefield.
• Isaac, Alistair M. C., 2013, “Modeling without Representation”, Synthese , 190(16): 3611–3623. doi:10.1007/s11229-012-0213-9
• Jebeile, Julie and Ashley Graham Kennedy, 2015, “Explaining with Models: The Role of Idealizations”, International Studies in the Philosophy of Science , 29(4): 383–392. doi:10.1080/02698595.2015.1195143
• Jones, Martin R., 2005, “Idealization and Abstraction: A Framework”, in Jones and Cartwright 2005: 173–217. doi:10.1163/9789401202732_010
• Jones, Martin R. and Nancy Cartwright (eds.), 2005, Idealization XII: Correcting the Model (Poznań Studies in the Philosophy of the Sciences and the Humanities 86), Amsterdam and New York: Rodopi. doi:10.1163/9789401202732
• Kelvin, William Thomson, Baron, 1884 [1987], Notes of lectures on molecular dynamics and the wave theory of light. Delivered at the Johns Hopkins University, Baltimore (aka Lord Kelvin’s Baltimore Lectures), A. S. Hathaway (recorder). A revised version was published in 1904, London: C.J. Clay and Sons. Reprint of the 1884 version in Robert Kargon and Peter Achinstein (eds.), Kelvin’s Baltimore Lectures and Modern Theoretical Physics , Cambridge, MA: MIT Press, 1987.
• Khalifa, Kareem, 2017, Understanding, Explanation, and Scientific Knowledge , Cambridge: Cambridge University Press. doi:10.1017/9781108164276
• Klein, Dominik, Johannes Marx, and Kai Fischbach, 2018, “Agent-Based Modeling in Social Science History and Philosophy: An Introduction”, Historical Social Research , 43(1): 243–258.
• Knuuttila, Tarja, 2005, “Models, Representation, and Mediation”, Philosophy of Science , 72(5): 1260–1271. doi:10.1086/508124
• –––, 2011, “Modelling and Representing: An Artefactual Approach to Model-Based Representation”, Studies in History and Philosophy of Science Part A , 42(2): 262–271. doi:10.1016/j.shpsa.2010.11.034
• Kroes, Peter, 1989, “Structural Analogies Between Physical Systems”, The British Journal for the Philosophy of Science , 40(2): 145–154. doi:10.1093/bjps/40.2.145
• Lange, Marc, 2015, “On ‘Minimal Model Explanations’: A Reply to Batterman and Rice”, Philosophy of Science , 82(2): 292–305. doi:10.1086/680488
• Lavis, David A., 2008, “Boltzmann, Gibbs, and the Concept of Equilibrium”, Philosophy of Science , 75(5): 682–692. doi:10.1086/594514
• Laymon, Ronald, 1982, “Scientific Realism and the Hierarchical Counterfactual Path from Data to Theory”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1982(1): 107–121. doi:10.1086/psaprocbienmeetp.1982.1.192660
• –––, 1985, “Idealizations and the Testing of Theories by Experimentation”, in Peter Achinstein and Owen Hannaway (eds.), Observation, Experiment, and Hypothesis in Modern Physical Science , Cambridge, MA: MIT Press, pp. 147–173.
• –––, 1991, “Thought Experiments by Stevin, Mach and Gouy: Thought Experiments as Ideal Limits and Semantic Domains”, in Horowitz and Massey 1991: 167–191.
• Leonelli, Sabina, 2010, “Packaging Small Facts for Re-Use: Databases in Model Organism Biology”, in Peter Howlett and Mary S. Morgan (eds.), How Well Do Facts Travel? The Dissemination of Reliable Knowledge , Cambridge: Cambridge University Press, pp. 325–348. doi:10.1017/CBO9780511762154.017
• –––, 2016, Data-Centric Biology: A Philosophical Study , Chicago, IL, and London: University of Chicago Press.
• –––, 2019, “What Distinguishes Data from Models?”, European Journal for Philosophy of Science , 9(2): article 22. doi:10.1007/s13194-018-0246-0
• Leonelli, Sabina and Rachel A. Ankeny, 2012, “Re-Thinking Organisms: The Impact of Databases on Model Organism Biology”, Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences , 43(1): 29–36. doi:10.1016/j.shpsc.2011.10.003
• Leplin, Jarrett, 1980, “The Role of Models in Theory Construction”, in Thomas Nickles (ed.), Scientific Discovery, Logic, and Rationality (Boston Studies in the Philosophy of Science 56), Dordrecht: Springer Netherlands, 267–283. doi:10.1007/978-94-009-8986-3_12
• Levy, Arnon, 2012, “Models, Fictions, and Realism: Two Packages”, Philosophy of Science , 79(5): 738–748. doi:10.1086/667992
• –––, 2015, “Modeling without Models”, Philosophical Studies , 172(3): 781–798. doi:10.1007/s11098-014-0333-9
• Levy, Arnon and Adrian Currie, 2015, “Model Organisms Are Not (Theoretical) Models”, The British Journal for the Philosophy of Science , 66(2): 327–348. doi:10.1093/bjps/axt055
• Levy, Arnon and Peter Godfrey-Smith (eds.), 2020, The Scientific Imagination: Philosophical and Psychological Perspectives , New York: Oxford University Press.
• Liefke, Kristina and Stephan Hartmann, 2018, “Intertheoretic Reduction, Confirmation, and Montague’s Syntax–Semantics Relation”, Journal of Logic, Language and Information , 27(4): 313–341. doi:10.1007/s10849-018-9272-8
• Lipton, Peter, 2009, “Understanding without Explanation”, in de Regt, Leonelli, and Eigner 2009: 43–63.
• Luczak, Joshua, 2017, “Talk about Toy Models”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 57: 1–7. doi:10.1016/j.shpsb.2016.11.002
• Magnani, Lorenzo, 2012, “Scientific Models Are Not Fictions: Model-Based Science as Epistemic Warfare”, in Lorenzo Magnani and Ping Li (eds.), Philosophy and Cognitive Science: Western & Eastern Studies (Studies in Applied Philosophy, Epistemology and Rational Ethics 2), Berlin and Heidelberg: Springer, pp. 1–38. doi:10.1007/978-3-642-29928-5_1
• Magnani, Lorenzo and Claudia Casadio (eds.), 2016, Model-Based Reasoning in Science and Technology: Logical, Epistemological, and Cognitive Issues (Studies in Applied Philosophy, Epistemology and Rational Ethics 27), Cham: Springer International Publishing. doi:10.1007/978-3-319-38983-7
• Magnani, Lorenzo and Nancy J. Nersessian (eds.), 2002, Model-Based Reasoning: Science, Technology, Values , Boston, MA: Springer US. doi:10.1007/978-1-4615-0605-8
• Magnani, Lorenzo, Nancy J. Nersessian, and Paul Thagard (eds.), 1999, Model-Based Reasoning in Scientific Discovery , Boston, MA: Springer US. doi:10.1007/978-1-4615-4813-3
• Mäki, Uskali, 1994, “Isolation, Idealization and Truth in Economics”, in Bert Hamminga and Neil B. De Marchi (eds.), Idealization VI: Idealization in Economics (Poznań Studies in the Philosophy of the Sciences and the Humanities 38), Amsterdam: Rodopi, pp. 147–168.
• Massimi, Michela, 2017, “Perspectivism”, in Juha Saatsi (ed.), The Routledge Handbook of Scientific Realism , London: Routledge, pp. 164–175.
• –––, 2018a, “Four Kinds of Perspectival Truth”, Philosophy and Phenomenological Research , 96(2): 342–359. doi:10.1111/phpr.12300
• –––, 2018b, “Perspectival Modeling”, Philosophy of Science , 85(3): 335–359. doi:10.1086/697745
• –––, 2019, “Two Kinds of Exploratory Models”, Philosophy of Science , 86(5): 869–881. doi:10.1086/705494
• Massimi, Michela and Casey D. McCoy (eds.), 2019, Understanding Perspectivism: Scientific Challenges and Methodological Prospects , New York: Routledge. doi:10.4324/9781315145198
• Mayo, Deborah, 1996, Error and the Growth of Experimental Knowledge , Chicago, IL: University of Chicago Press.
• –––, 2018, Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars , Cambridge: Cambridge University Press. doi:10.1017/9781107286184
• McMullin, Ernan, 1968, “What Do Physical Models Tell Us?”, in B. Van Rootselaar and J. Frits Staal (eds.), Logic, Methodology and Philosophy of Science III (Studies in Logic and the Foundations of Mathematics 52), Amsterdam: North Holland, pp. 385–396. doi:10.1016/S0049-237X(08)71206-0
• –––, 1985, “Galilean Idealization”, Studies in History and Philosophy of Science Part A , 16(3): 247–273. doi:10.1016/0039-3681(85)90003-2
• Morgan, Mary S., 1999, “Learning from Models”, in Morgan and Morrison 1999: 347–388. doi:10.1017/CBO9780511660108.013
• Morgan, Mary S. and Marcel J. Boumans, 2004, “Secrets Hidden by Two-Dimensionality: The Economy as a Hydraulic Machine”, in Soraya de Chadarevian and Nick Hopwood (eds.), Model: The Third Dimension of Science , Stanford, CA: Stanford University Press, pp. 369–401.
• Morgan, Mary S. and Margaret Morrison (eds.), 1999, Models as Mediators: Perspectives on Natural and Social Science , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511660108
• Morrison, Margaret, 1999, “Models as Autonomous Agents”, in Morgan and Morrison 1999: 38–65. doi:10.1017/CBO9780511660108.004
• –––, 2000, Unifying Scientific Theories: Physical Concepts and Mathematical Structures , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511527333
• –––, 2005, “Approximating the Real: The Role of Idealizations in Physical Theory”, in Jones and Cartwright 2005: 145–172. doi:10.1163/9789401202732_009
• –––, 2009, “Understanding in Physics and Biology: From the Abstract to the Concrete”, in de Regt, Leonelli, and Eigner 2009: 123–145.
• –––, 2012, “Emergent Physics and Micro-Ontology”, Philosophy of Science , 79(1): 141–166. doi:10.1086/663240
• Musgrave, Alan, 1981, “‘Unreal Assumptions’ in Economic Theory: The F-Twist Untwisted”, Kyklos , 34(3): 377–387. doi:10.1111/j.1467-6435.1981.tb01195.x
• Nagel, Ernest, 1961, The Structure of Science: Problems in the Logic of Scientific Explanation , New York: Harcourt, Brace and World.
• Nersessian, Nancy J., 1999, “Model-Based Reasoning in Conceptual Change”, in Magnani, Nersessian, and Thagard 1999: 5–22. doi:10.1007/978-1-4615-4813-3_1
• –––, 2010, Creating Scientific Concepts , Cambridge, MA: MIT Press.
• Nguyen, James, forthcoming, “It’s Not a Game: Accurate Representation with Toy Models”, The British Journal for the Philosophy of Science , first online: 23 March 2019. doi:10.1093/bjps/axz010
• Nguyen, James and Roman Frigg, forthcoming, “Mathematics Is Not the Only Language in the Book of Nature”, Synthese , first online: 28 August 2017. doi:10.1007/s11229-017-1526-5
• Norton, John D., 1991, “Thought Experiments in Einstein’s Work”, in Horowitz and Massey 1991: 129–148.
• –––, 2003, “Causation as Folk Science”, Philosopher’s Imprint , 3: article 4. [ Norton 2003 available online ]
• –––, 2012, “Approximation and Idealization: Why the Difference Matters”, Philosophy of Science , 79(2): 207–232. doi:10.1086/664746
• Nowak, Leszek, 1979, The Structure of Idealization: Towards a Systematic Interpretation of the Marxian Idea of Science , Dordrecht: D. Reidel.
• Palacios, Patricia, 2019, “Phase Transitions: A Challenge for Intertheoretic Reduction?”, Philosophy of Science , 86(4): 612–640. doi:10.1086/704974
• Peschard, Isabelle, 2011, “Making Sense of Modeling: Beyond Representation”, European Journal for Philosophy of Science , 1(3): 335–352. doi:10.1007/s13194-011-0032-8
• Piccinini, Gualtiero and Carl Craver, 2011, “Integrating Psychology and Neuroscience: Functional Analyses as Mechanism Sketches”, Synthese , 183(3): 283–311. doi:10.1007/s11229-011-9898-4
• Pincock, Christopher, 2012, Mathematics and Scientific Representation , Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780199757107.001.0001
• –––, forthcoming, “Concrete Scale Models, Essential Idealization and Causal Explanation”, British Journal for the Philosophy of Science .
• Portides, Demetris P., 2007, “The Relation between Idealisation and Approximation in Scientific Model Construction”, Science & Education , 16(7–8): 699–724. doi:10.1007/s11191-006-9001-6
• –––, 2014, “How Scientific Models Differ from Works of Fiction”, in Lorenzo Magnani (ed.), Model-Based Reasoning in Science and Technology (Studies in Applied Philosophy, Epistemology and Rational Ethics 8), Berlin and Heidelberg: Springer, pp. 75–87. doi:10.1007/978-3-642-37428-9_5
• Potochnik, Angela, 2007, “Optimality Modeling and Explanatory Generality”, Philosophy of Science , 74(5): 680–691.
• –––, 2017, Idealization and the Aims of Science , Chicago, IL: University of Chicago Press.
• Poznic, Michael, 2016, “Make-Believe and Model-Based Representation in Science: The Epistemology of Frigg’s and Toon’s Fictionalist Views of Modeling”, Teorema: Revista Internacional de Filosofía , 35(3): 201–218.
• Psillos, Stathis, 1995, “The Cognitive Interplay between Theories and Models: The Case of 19th Century Optics”, in Herfel et al. 1995: 105–133.
• Redhead, Michael, 1980, “Models in Physics”, The British Journal for the Philosophy of Science , 31(2): 145–163. doi:10.1093/bjps/31.2.145
• Reiss, Julian, 2003, “Causal Inference in the Abstract or Seven Myths about Thought Experiments”, in Causality: Metaphysics and Methods Research Project , Technical Report 03/02. London: London School of Economics.
• –––, 2006, “Social Capacities”, in Hartmann et al. 2006: 265–288.
• –––, 2012, “The Explanation Paradox”, Journal of Economic Methodology , 19(1): 43–62. doi:10.1080/1350178X.2012.661069
• Reutlinger, Alexander, 2017, “Do Renormalization Group Explanations Conform to the Commonality Strategy?”, Journal for General Philosophy of Science , 48(1): 143–150. doi:10.1007/s10838-016-9339-7
• Reutlinger, Alexander, Dominik Hangleiter, and Stephan Hartmann, 2018, “Understanding (with) Toy Models”, The British Journal for the Philosophy of Science , 69(4): 1069–1099. doi:10.1093/bjps/axx005
• Rice, Collin C., 2015, “Moving Beyond Causes: Optimality Models and Scientific Explanation”, Noûs , 49(3): 589–615. doi:10.1111/nous.12042
• –––, 2016, “Factive Scientific Understanding without Accurate Representation”, Biology & Philosophy , 31(1): 81–102. doi:10.1007/s10539-015-9510-2
• –––, 2018, “Idealized Models, Holistic Distortions, and Universality”, Synthese , 195(6): 2795–2819. doi:10.1007/s11229-017-1357-4
• –––, 2019, “Models Don’t Decompose That Way: A Holistic View of Idealized Models”, The British Journal for the Philosophy of Science , 70(1): 179–208. doi:10.1093/bjps/axx045
• Rosaler, Joshua, 2015, “Local Reduction in Physics”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 50: 54–69. doi:10.1016/j.shpsb.2015.02.004
• Rueger, Alexander, 2005, “Perspectival Models and Theory Unification”, The British Journal for the Philosophy of Science , 56(3): 579–594. doi:10.1093/bjps/axi128
• Rueger, Alexander and David Sharp, 1998, “Idealization and Stability: A Perspective from Nonlinear Dynamics”, in Shanks 1998: 201–216.
• Saatsi, Juha, 2016, “Models, Idealisations, and Realism”, in Emiliano Ippoliti, Fabio Sterpetti, and Thomas Nickles (eds.), Models and Inferences in Science (Studies in Applied Philosophy, Epistemology and Rational Ethics 25), Cham: Springer International Publishing, pp. 173–189. doi:10.1007/978-3-319-28163-6_10
• Saatsi, Juha and Alexander Reutlinger, 2018, “Taking Reductionism to the Limit: How to Rebut the Antireductionist Argument from Infinite Limits”, Philosophy of Science , 85(3): 455–482. doi:10.1086/697735
• Salis, Fiora, forthcoming, “The New Fiction View of Models”, The British Journal for the Philosophy of Science , first online: 20 April 2019. doi:10.1093/bjps/axz015
• Salmon, Wesley C., 1984, Scientific Explanation and the Causal Structure of the World , Princeton, NJ: Princeton University Press.
• Schaffner, Kenneth F., 1969, “The Watson–Crick Model and Reductionism”, The British Journal for the Philosophy of Science , 20(4): 325–348. doi:10.1093/bjps/20.4.325
• Scheibe, Erhard, 1997, Die Reduktion physikalischer Theorien: Ein Beitrag zur Einheit der Physik, Teil I: Grundlagen und elementare Theorie , Berlin: Springer.
• –––, 1999, Die Reduktion physikalischer Theorien: Ein Beitrag zur Einheit der Physik, Teil II: Inkommensurabilität und Grenzfallreduktion , Berlin: Springer.
• –––, 2001, Between Rationalism and Empiricism: Selected Papers in the Philosophy of Physics , Brigitte Falkenburg (ed.), New York: Springer. doi:10.1007/978-1-4613-0183-7
• Shanks, Niall (ed.), 1998, Idealization in Contemporary Physics , Amsterdam: Rodopi.
• Shech, Elay, 2018, “Idealizations, Essential Self-Adjointness, and Minimal Model Explanation in the Aharonov–Bohm Effect”, Synthese , 195(11): 4839–4863. doi:10.1007/s11229-017-1428-6
• Sismondo, Sergio and Snait Gissis (eds.), 1999, Modeling and Simulation , Special Issue of Science in Context , 12(2).
• Sorensen, Roy A., 1992, Thought Experiments , New York: Oxford University Press. doi:10.1093/019512913X.001.0001
• Spector, Marshall, 1965, “Models and Theories”, The British Journal for the Philosophy of Science , 16(62): 121–142. doi:10.1093/bjps/XVI.62.121
• Staley, Kent W., 2004, The Evidence for the Top Quark: Objectivity and Bias in Collaborative Experimentation , Cambridge: Cambridge University Press.
• Sterrett, Susan G., 2006, “Models of Machines and Models of Phenomena”, International Studies in the Philosophy of Science , 20(1): 69–80. doi:10.1080/02698590600641024
• –––, forthcoming, “Scale Modeling”, in Diane Michelfelder and Neelke Doorn (eds.), Routledge Handbook of Philosophy of Engineering , Chapter 32. [ Sterrett forthcoming available online ]
• Strevens, Michael, 2004, “The Causal and Unification Approaches to Explanation Unified—Causally”, Noûs , 38(1): 154–176. doi:10.1111/j.1468-0068.2004.00466.x
• –––, 2008, Depth: An Account of Scientific Explanation , Cambridge, MA, and London: Harvard University Press.
• –––, 2013, Tychomancy: Inferring Probability from Causal Structure , Cambridge, MA, and London: Harvard University Press.
• Suárez, Mauricio, 2003, “Scientific Representation: Against Similarity and Isomorphism”, International Studies in the Philosophy of Science , 17(3): 225–244. doi:10.1080/0269859032000169442
• –––, 2004, “An Inferential Conception of Scientific Representation”, Philosophy of Science , 71(5): 767–779. doi:10.1086/421415
• ––– (ed.), 2009, Fictions in Science: Philosophical Essays on Modeling and Idealization , London: Routledge. doi:10.4324/9780203890103
• Sugden, Robert, 2000, “Credible Worlds: The Status of Theoretical Models in Economics”, Journal of Economic Methodology , 7(1): 1–31. doi:10.1080/135017800362220
• Sullivan, Emily and Kareem Khalifa, 2019, “Idealizations and Understanding: Much Ado About Nothing?”, Australasian Journal of Philosophy , 97(4): 673–689. doi:10.1080/00048402.2018.1564337
• Suppe, Frederick, 2000, “Theory Identity”, in William H. Newton-Smith (ed.), A Companion to the Philosophy of Science , Oxford: Wiley-Blackwell, pp. 525–527.
• Suppes, Patrick, 1960, “A Comparison of the Meaning and Uses of Models in Mathematics and the Empirical Sciences”, Synthese , 12(2–3): 287–301. Reprinted in Freudenthal 1961: 163–177, and in Suppes 1969: 10–23. doi:10.1007/BF00485107 doi:10.1007/978-94-010-3667-2_16
• –––, 1962, “Models of Data”, in Ernest Nagel, Patrick Suppes, and Alfred Tarski (eds.), Logic, Methodology and Philosophy of Science: Proceedings of the 1960 International Congress , Stanford, CA: Stanford University Press, pp. 252–261. Reprinted in Suppes 1969: 24–35.
• –––, 1969, Studies in the Methodology and Foundations of Science: Selected Papers from 1951 to 1969 , Dordrecht: Reidel.
• –––, 2007, “Statistical Concepts in Philosophy of Science”, Synthese , 154(3): 485–496. doi:10.1007/s11229-006-9122-0
• Swoyer, Chris, 1991, “Structural Representation and Surrogative Reasoning”, Synthese , 87(3): 449–508. doi:10.1007/BF00499820
• Tabor, Michael, 1989, Chaos and Integrability in Nonlinear Dynamics: An Introduction , New York: John Wiley.
• Teller, Paul, 2001, “Twilight of the Perfect Model”, Erkenntnis , 55(3): 393–415. doi:10.1023/A:1013349314515
• –––, 2002, “Critical Study: Nancy Cartwright’s The Dappled World: A Study of the Boundaries of Science ”, Noûs , 36(4): 699–725. doi:10.1111/1468-0068.t01-1-00408
• –––, 2009, “Fictions, Fictionalization, and Truth in Science”, in Suárez 2009: 235–247.
• –––, 2018, “Referential and Perspectival Realism”, Spontaneous Generations: A Journal for the History and Philosophy of Science , 9(1): 151–164. doi:10.4245/sponge.v9i1.26990
• Tešić, Marko, 2019, “Confirmation and the Generalized Nagel–Schaffner Model of Reduction: A Bayesian Analysis”, Synthese , 196(3): 1097–1129. doi:10.1007/s11229-017-1501-1
• Thomasson, Amie L., 1999, Fiction and Metaphysics , New York: Cambridge University Press. doi:10.1017/CBO9780511527463
• –––, 2020, “If Models Were Fictions, Then What Would They Be?”, in Levy and Godfrey-Smith 2020: 51–74.
• Thomson-Jones, Martin, 2006, “Models and the Semantic View”, Philosophy of Science , 73(5): 524–535. doi:10.1086/518322
• –––, 2020, “Realism about Missing Systems”, in Levy and Godfrey-Smith 2020: 75–101.
• Toon, Adam, 2012, Models as Make-Believe: Imagination, Fiction and Scientific Representation , Basingstoke: Palgrave Macmillan.
• Trout, J. D., 2002, “Scientific Explanation and the Sense of Understanding”, Philosophy of Science , 69(2): 212–233. doi:10.1086/341050
• van Fraassen, Bas C., 1989, Laws and Symmetry , Oxford: Oxford University Press. doi:10.1093/0198248601.001.0001
• Walton, Kendall L., 1990, Mimesis as Make-Believe: On the Foundations of the Representational Arts , Cambridge, MA: Harvard University Press.
• Weisberg, Michael, 2007, “Three Kinds of Idealization”, Journal of Philosophy , 104(12): 639–659. doi:10.5840/jphil20071041240
• –––, 2013, Simulation and Similarity: Using Models to Understand the World , Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780199933662.001.0001
• Weisberg, Michael and Ryan Muldoon, 2009, “Epistemic Landscapes and the Division of Cognitive Labor”, Philosophy of Science , 76(2): 225–252. doi:10.1086/644786
• Wimsatt, William, 1987, “False Models as Means to Truer Theories”, in Matthew Nitecki and Antoni Hoffman (eds.), Neutral Models in Biology , Oxford: Oxford University Press, pp. 23–55.
• –––, 2007, Re-Engineering Philosophy for Limited Beings: Piecewise Approximations to Reality , Cambridge, MA: Harvard University Press.
• Woodward, James, 2003, Making Things Happen: A Theory of Causal Explanation , Oxford: Oxford University Press. doi:10.1093/0195155270.001.0001
• Woody, Andrea I., 2004, “More Telltale Signs: What Attention to Representation Reveals about Scientific Explanation”, Philosophy of Science , 71(5): 780–793. doi:10.1086/421416
• Zollman, Kevin J. S., 2007, “The Communication Structure of Epistemic Communities”, Philosophy of Science , 74(5): 574–587. doi:10.1086/525605

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• Internet Encyclopedia of Philosophy article on models
• Bibliography (1450–2008), Mueller Science
• Interactive models from various sciences (Phet, University of Colorado, Boulder)
• Models of the global climate (Climate.gov)
• Double-helix model of DNA (Proteopedia)
• A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution (Sarah Otto and Troy Day)
• Lotka–Volterra model (analyticphysics.com)
• Schelling’s Model of Segregation (Frank McCown)
• Modeling Commons (NetLogo)
• Social and Economic Networks: Models and Analysis (Stanford Online course)
• Neural Network Models (TensorFlow)

analogy and analogical reasoning | laws of nature | science: unity of | scientific explanation | scientific realism | scientific representation | scientific theories: structure of | simulations in science | thought experiments

Acknowledgments

We would like to thank Joe Dewhurst, James Nguyen, Alexander Reutlinger, Collin Rice, Dunja Šešelja, and Paul Teller for helpful comments on the drafts of the revised version in 2019. When writing the original version back in 2006 we benefitted from comments and suggestions by Nancy Cartwright, Paul Humphreys, Julian Reiss, Elliott Sober, Chris Swoyer, and Paul Teller.

Copyright © 2020 by Roman Frigg < r . p . frigg @ lse . ac . uk > Stephan Hartmann < stephan . hartmann @ lrz . uni-muenchen . de >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2024 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

The Scientific Hypothesis

The Key to Understanding How Science Works

Hypotheses, Theories, Laws (and Models)… What’s the difference?

Untold hours have been spent trying to sort out the differences between these ideas. should we bother.

Ask what the differences between these concepts are and you’re likely to encounter a raft of distinctions; typically with charts and ladders of generality leading from hypotheses to theories and, ultimately, to laws.   Countless students have been exposed to and forced to learn how the schemes are set up.  Theories are said to be well-tested hypotheses, or maybe whole collections of linked hypotheses, and laws, well, laws are at the top of the heap, the apex of science having enormous reach, quantitative predictive power, and validity.  It all seems so clear.

Yet there are many problems with the general scheme.  For one thing, it is never quite explained how a hypothesis turns into a theory or law and, consequently, the boundaries are blurry, and definitions tend vary with the speaker.  And there is no consistency in usage across fields, I’ll give some examples in a minute.  There are branches of science that have few if any theories and no laws – neuroscience comes to mind – though no one doubts that neuroscience is a bona fide science that has discovered great quantities of reliable and useful information and wide-ranging generalizations.  At the other extreme, there are sciences that spin out theories at a dizzying pace – psychology, for instance – although the permanence and indeed the veracity of psychological theories are rarely on par with those of physics or chemistry.

Some people will tell you that theories and laws are “more quantitative” than hypotheses, but the most famous theory in biology, the Theory of Evolution, which is based on concepts such as heritability, genetic variability, natural selection, etc. is not as neatly expressible in quantitative terms as is Newton’s Theory of Gravity, for example.   And what do we make of the fact that Newton’s “Law of Gravity” was superceded by Einstein’s “General Theory (not Law) of Relativity?”

What about the idea that a hypothesis is a low-level explanation that somehow transmogrifies into a theory when conditions are right?  Even this simple rule is not adhered to.  Take geology (or “geoscience” nowadays):  We have the Alvarez Hypothesis about how an asteroid slamming into the earth caused the extinction of dinosaurs and other life-forms ~66 million years ago.  The Alvarez Hypothesis explains, often in quantitative detail, many important phenomena and makes far-reaching predictions, most remarkably of a crater, which was eventually found in the Yucatan peninsula, that has the right age and size to be the site of an extinction-causing asteroid impact.  The Alvarez Hypothesis has been rigorously tested many times since it was proposed, without having been promoted to a theory. 

But perhaps the Alvarez Hypothesis is still thought to be a tentative explanation, not yet worthy of a more exalted status? It seems that the same can’t be said about the idea that the earth’s crust consists of 12 or so rigid “plates” of solid material that drift around very slowly and create geological phenomena, such as mountain ranges and earth-quakes, when they crash into each other.  This is called either the “Plate Tectonics Hypothesis” or “Plate Tectonics Theory” by different authors.  Same data, same interpretations, same significance, different names. 

And for anyone trying to make sense of the hypothesis-theory-law progression, it must be highly confusing to learn that the crowning achievement of modern physics – itself the “queen of the sciences” – is a complex, extraordinarily precise, quantitative structure is known as the Standard Model of Particle Physics, not the Standard Theory, or the Standard Law!  The Standard Model incorporates three of the four major forces of nature, describes many subatomic particles, and has successfully predicted numerous subtle properties of subatomic particles.  Does this mean that “model” now implies a large, well-worked out and self-consistent body of scientific knowledge?  Not at all; in fact, “model” and “hypothesis” are used interchangeably at the simplest levels of experimental investigation in biology, neuroscience, etc., so definition-wise, we’re back to the beginning.

The reason that the Standard Model is a model and not a theory seems basically to be the same as the reason that the Alvarez Hypothesis is a hypothesis and not a theory or that Evolution is a theory and not a law:  essentially it is a matter of convention, tradition, or convenience.  The designations, we can infer, are primarily names that lack exact substantive, generally agreed-on definitions.

So, rather than worrying about any profound distinctions between hypotheses, theories, laws (and models) it might be more helpful to look at the properties that they have in common:

1. They are all “conjectural” which, for the moment, means that they are inventions of the human mind.

2. They make specific predictions that are empirically testable, in principle.

3. They are falsifiable – if their predictions are false, they are false – though not provable, by experiment or observation. 

4.  As a consequence of point 3., hypotheses, theories, and laws are all provisional; they may be replaced as further information becomes available. 

“Hypothesis,” it seems to me, is the fundamental unit, the building block, of scientific thinking. It is the term that is most consistently used by all sciences; it is more basic than any theory; it carries the least baggage, is the least susceptible to multiple interpretations and, accordingly, is the most likely to communicate effectively.  These advantages are relative of course; as I’ll get into elsewhere, even “hypothesis” is the subject of misinterpretation. In any case, its simplicity and clarity are why this website is devoted to the Scientific Hypothesis and not the others.

Leave a Reply Cancel reply

You must be logged in to post a comment.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Multiscale models driving hypothesis and theory-based research in microbial ecology

Eloi martinez-rabert, william t sloan, rebeca gonzalez-cabaleiro.

• Author information
• Article notes
• Copyright and License information

One contribution of 7 to a theme issue ‘ Microbial ecology for engineering biology (Part II) ’.

Corresponding author.

Received 2023 Feb 13; Accepted 2023 Mar 17; Collection date 2023 Aug 6.

Published by the Royal Society under the terms of the Creative Commons Attribution License http://creativecommons.org/licenses/by/4.0/ , which permits unrestricted use, provided the original author and source are credited.

Hypothesis and theory-based studies in microbial ecology have been neglected in favour of those that are descriptive and aim for data-gathering of uncultured microbial species. This tendency limits our capacity to create new mechanistic explanations of microbial community dynamics, hampering the improvement of current environmental biotechnologies. We propose that a multiscale modelling bottom-up approach (piecing together sub-systems to give rise to more complex systems) can be used as a framework to generate mechanistic hypotheses and theories ( in-silico bottom-up methodology). To accomplish this, formal comprehension of the mathematical model design is required together with a systematic procedure for the application of the in-silico bottom-up methodology. Ruling out the belief that experimentation before modelling is indispensable, we propose that mathematical modelling can be used as a tool to direct experimentation by validating theoretical principles of microbial ecology. Our goal is to develop methodologies that effectively integrate experimentation and modelling efforts to achieve superior levels of predictive capacity.

Keywords: mathematical modelling, in-silico bottom-up methodology, microbial communities, microbial ecology

1. Introduction

Hypothesis testing as a scientific approach in environmental microbiology and biotechnology is bounded by the intrinsic complexity of microbial communities. Theory-based research is relegated by an increasing number of microbial ecology studies that focus on descriptive experiments of uncultured microbial species. However, critically testing ecological hypotheses requires rigorous experimental design while the application of novel molecular technologies for data collection has led to a multitude of top-down research approaches where data are just described [ 1 ]. Generation of knowledge through induction (e.g. accumulative characterization of uncultured microbial species) does not per se translate in new theoretical/mechanistic explanations for community assembly or specific fitness traits.

We propose the development of research focused on microbial ecology quantification, which driven by theoretical hypotheses, is further validated by interplay within mathematical modelling and laboratory experimentation. We describe a modelling methodology based on a bottom-up approach (piecing together sub-systems to give rise to more complex systems) in order to generate, together with experimental validation, new hypotheses and theories. By using theoretical platforms, we can target the minimization of complexity associated with natural communities directing research exploration in a more efficient way. To understand the implications associated with this methodology, we first discuss the actual position of mathematical models and experimentation in scientific research.

2. Experimental and theoretical models

Considering that any mathematical model represents a conceptualization of reality, it is commonly assumed that experiments should precede any modelling exercise. Modelling is then mostly placed as an alternative complement to experimentation because theoretical results must be demonstrated or validated. Nevertheless, experimental outcomes must also be demonstrated by replication and reproducibility as a major principle underpinning the scientific method. The results obtained by an experiment, an observational study, or in a statistical analysis of a dataset can be considered reliable only if these studies are replicated [ 2 ].

Experimentation and modelling exercises might not be seen as exclusive, but interconnected methodologies ( figure 1 ). A modelling exercise can help in defining experimental designs that validate hypotheses theoretically constructed (dotted arrow, figure 1 ). This level of definition also aids reproducibility, especially when applied to complex systems. It can be argued that the most useful models are constructed on the basis of the theoretical knowledge we possess [ 3 , 4 ], directing experimentation that aims at validating the principles on which they are built, that is, using mathematical models as hypotheses generator.

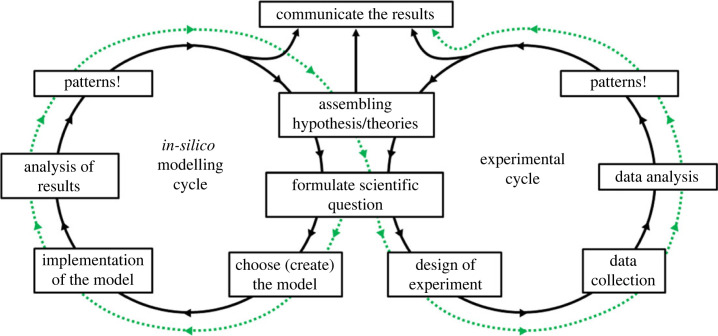
Modelling–experimental cycle. Integrated development of experimental and modelling methodologies can lead to higher levels of predictive capacities and operation control. Dotted arrow depicts the methodology presented here—theoretical model before experimentation.

3. In-silico bottom-up methodology

When modelling continuous and complex natural processes, they can be treated as a group of discrete elements interconnected able to define observable events that can be measured. A bottom-up approach is essentially piecing together sub-systems to give rise to more complex systems. In-silico models that follow a bottom-up approach aim to explain how emerging properties of complex communities arise from simpler processes [ 5 ].

The first step to build an in-silico bottom-up methodology is to identify all the elements that describe a particular phenomenon (i.e. the fragmentation ; figure 2 ). After that, the elements that will be part of the model are selected. For this step having enough information is crucial, either providing enough specific experimental data or by means of construction of theories and first principles (generally associated with a set of mathematical equations). Additionally, in the process of selection of elements one must consider and evaluate the model complexity and the possibilities for experimental validation [ 6 ]. Subsequently, the mathematical model is assembled . A mathematical model is a conceptual representation of a mechanism (or a collection of them) limited by our knowledge about the reality. All models are constituted by the quintuple:

Domain ( D ): set of factual items (elements and processes) that constitute the studied system.

Scientific question ( Q ): question(s) that states the reason for modelling and the construction of the model.

Interpretation ( I ): validated explanations of each item of the domain . Definition of spatial scale(s) and temporal extent is included here.

Assumptions ( A ): set of explicitly stated (or implicit premised) conventions and choices that fulfils the holes in our interpretation of reality. These establish the limits of our model and simplify the problem (e.g. by ignoring some processes or elements that cannot be well described).

Formalism ( F ): set of mathematical expressions that represent the items of the domain .

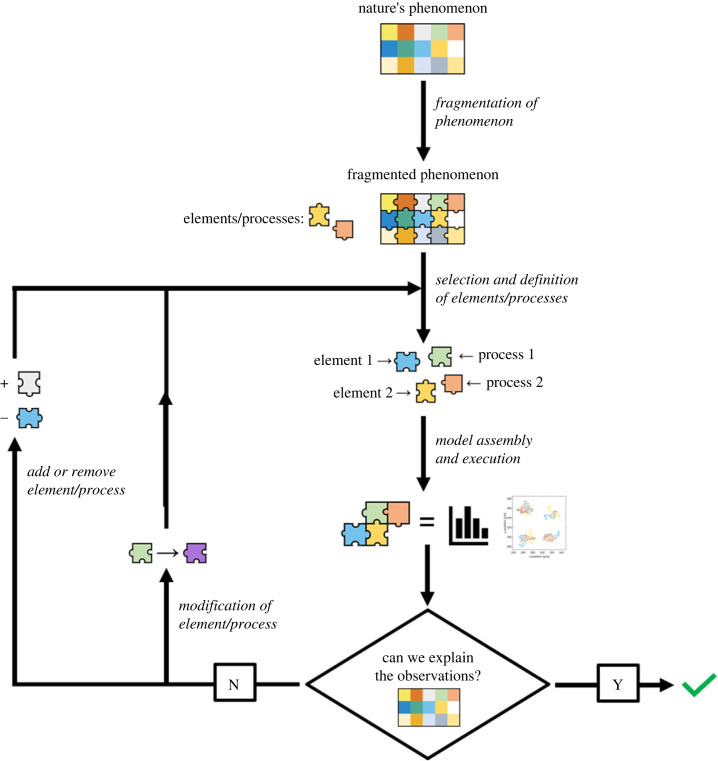
Schematic of in-silico bottom-up methodology.

The definition of each of the components 〈 D , Q , I , A , F 〉 is fundamental for the success of the modelling process. The construction of the mathematical model starts with the abstraction of the current knowledge about the domain ( D ). Based on our understanding, the scientific question ( Q ) is stated. Then, the formalization of our knowledge about the domain is addressed, defining interpretation, assumptions and formalism (i.e. the modelling approach, I , A , F ). Table 1 shows an example of the statement of 〈 D , Q , I , A , F 〉. The limits of the modelling approach 〈 I , A , F 〉 are established by the scope of the fundamental processes and the selected elements. The overlook of a key element or process can make our model inaccurate. An example of this is the omission of the diffusion in an aggregated system as presented in Model 1 in table 1 . Although an NH 3 -limiting environment was considered (this being one of the main pressure factors for the selection of Comammox process [ 7 ]), the enrichment observed in the Daims et al. study [ 8 ] was not predicted with Model 1 . Therefore, a model will be useful (i.e. generates reliable knowledge) if and only if there is no discrepancy between the results of the modelling approach 〈 I , A , F 〉 and the observations in the real domain ( D ).

Example of statement of model components 〈 D, Q, I, A, F 〉. Legend μ max , maximum specific growth rate; K NH 3 , half-saturation constant for NH 3 ; K O 2 , half-saturation constant for O 2 ; a m , specific maintenance rate; [NH 3 ], [O 2 ], substrate concentration; D , diffusion coefficient; R xy , reaction term in each discretized space; R BL , reaction term in bulk liquid; HRT, hydraulic retention time; X, bacteria concentration.

a Model performed with MATLAB (R2020b) via the built-in function ‘ode45()’.

b Source code is available on public GitHub repository at https://github.com/Computational-Platform-IbM/IbM .

The outcome from the computational model is validated using the available experimental data. If the model is accurate enough to represent the system of interest, we can use it for prediction and generation of new knowledge. New theoretical knowledge can be generated by the validation of the discrete elements and processes employed. To increase the accuracy of a mathematical model, we could (i) add (or remove) elements and/or processes that were previously overlooked or (ii) modify those previously selected (iterative procedure; figure 2 ).

4. Scales of modelling for microbial communities

We define three scales that are fundamental in the modelling of microbial communities: individual scale (main elements of the model), micro-scale (processes simulated at the same resolution as individual scale) and macro-scale (elements and processes described from a larger perspective, generally embedded in the bulk liquid region). Table 1 presents an example of these scales for the modelling of microbial aggregates.

The different scales of the model are interconnected and they influence each other. For example, the microbial activity is influenced by the local conditions stated by the micro-scale and, simultaneously, the microbial cells shape the local environment. The integration of multiple scales with different characteristic times (e.g. cell division: approximately 1 h; diffusion–reaction process: approximately 10 −8 h) is possible thanks to the use of proper time discretization and systematic resolution—a pseudo-steady state for processes with lower characteristic time is considered a good approximation for most applications when solving those with higher characteristic time [ 9 ]. Multiscale modelling also covers processes with a gap between characteristic space scales, such as diffusion–reaction process (approx. 10 −6 m) and the bulk processes (approx. 10 −3 –1 m). Because the characteristic time and space are positively correlated (ensuring the numerical condition stability), the systematic resolution presented above also deals with the gap between space scales.

4.1. Individual scale: models that describe individual microbial activity

In microbial ecology, Monod equation has been widely used to describe biological activity [ 10 , 11 ]. Growth is defined by empirical parameters measured for specific populations and conditions without considering the ecological interactions or microbial evolution that would explain the specific dominant activities observed in bioprocesses.

Aware of the limitations imposed by the use of Monod equation [ 12 ], molecular systems biology attempts to comprehend cell growth through mechanistic descriptions of intracellular processes. With different levels of metabolic and physiological detail, these descriptions are able to identify some fitness trade-offs in microbial activity arising from a common set of physicochemical and intracellular constraints. Resource allocation theory defines that microorganisms optimize the use of limited intracellular resources towards expressing the most efficient strategy for growth, allowing the description of their dynamic adaptations to the environment [ 13 ].

An approach like this requires in many cases detailed physiologic and metabolic information available, generating mathematical models that require a high number of parameters. This limits their application to a few model organisms [ 14 ]. A validation of a first-principles approach can overcome the reduced empirical information by attempting the prediction of kinetic parameters for growth through mathematical equations. For example, bioenergetics analyses provide a tool for quantifying growth yields [ 15 ]. Efforts towards estimating the trends of other kinetic parameters for description of microbial activity and growth can also be considered on a framework of resource allocation [ 16 ].

4.2. Micro-scale: prediction of emerging properties of communities

The integration of models that describe microbial growth with the definition of the local conditions dynamically affected by the microbial activity enables the description of interactions between the media, individuals and community. This allows the prediction of emergent properties that arise from the definition of individual activity [ 17 ], and possible estimation of ecological trends in communities that can be compared to experimental observations.

Depending on the scientific question asked, abiotic physicochemical processes should be considered. Examples of this are kinetic models of acid–base reactions, chemical speciation or precipitation. The consideration of spatial competition might also be crucial to describe ecological interactions in specific communities [ 4 ].

4.3. Macro-scale: scaling up and down key processes

Modelling large-scale systems with micro-scale resolution (approx. 10 −6 m) is computationally a very intensive task. To overcome this limitation, micro- and macro-scale processes are independently resolved following a systematic procedure through the establishment of pseudo-steady states [ 9 ]. The full integration of both spatial scales can be achieved if the micro-scale processes are scaled up, and the macro-scale processes are scaled down. The scaling-up is based on the consideration of a statistically representative volume of the larger system in full detail. It is assumed that the representative volume yields a representative influence on the whole system (i.e. the macro-scale). On the other hand, the scaling-down of macro-scale processes needs the definition of boundary conditions for the simulated system. Based on the goal that the model has (or the scientific question ( Q )), the boundary conditions can be set (i) unidirectionally (only macro-scale influences micro-scale; fixed boundary conditions) or (ii) bidirectionally (macro-scale influences micro-scale and vice versa; dynamic boundary conditions).

5. Conclusion

An alternative avenue to advance the understanding of microbial ecology, community assembly and biological activity would aim at the deconstruction of complexity by means of a bottom-up approach, where multiscale models, robust experimental data collection, and method development are integrated. In essence, we propose the design of cultivation-based experiments that help the validation of hypotheses constructed by mathematical modelling. Although hypothesis-based cultivation experiments can be seen as too idealistic when compared with the intrinsic complexity of microbial ecology, well-designed experiments with targeted scientific questions can lead to the discovery of new metabolic characteristics or relationships between species. In this context, the integration of molecular technologies would aid the validation of theoretical hypotheses. The rationalization of ecological interactions in a community, and their relation to the environment, breaks down complexity, reduces the necessity of data, and accelerates understanding [ 18 ]. This promises a higher level of prediction capacity which can directly impact on the engineering of bioprocesses. In this effort, commonalities between communities will be found, which implies that knowledge construction in one field will benefit others (e.g. research on anaerobic digestion processes and the understanding of gut microbiome or marine microbial communities).

Data accessibility

The source code is available on the public GitHub repository at https://github.com/Computational-Platform-IbM/IbM .

Authors' contributions

E.M.-R.: conceptualization, visualization, writing—original draft, writing—review and editing; W.T.S.: funding acquisition, writing—review and editing; R.G.-C.: conceptualization, funding acquisition, supervision, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

This work was supported by University of Glasgow James Watt EPSRC Scholarship (grant no. EP/R513222/1).

• 1. Prosser JI. 2020. Putting science back into microbial ecology: a question of approach. Phil. Trans. R. Soc. B 375, 20190240. ( 10.1098/rstb.2019.0240) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 2. Eric WKT, Kwan K-M. 1999. Replication and theory development in organizational science: a critical realist perspective. Acad. Manag. Rev. 24, 759-780. ( 10.2307/259353) [ DOI ] [ Google Scholar ]
• 3. Kreft JU. 2004. Biofilms promote altruism. Microbiology (Reading) 150, 2751-2760. ( 10.1099/mic.0.26829-0) [ DOI ] [ PubMed ] [ Google Scholar ]
• 4. Martinez-Rabert E, van Amstel C, Smith C, Sloan WT, Gonzalez-Cabaleiro R. 2022. Environmental and ecological controls of the spatial distribution of microbial populations in aggregates. PLoS Comput. Biol. 18, e1010807. ( 10.1371/journal.pcbi.1010807) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 5. Rodríguez Amor D, Dal Bello M. 2019. Bottom-up approaches to synthetic cooperation in microbial communities. Life (Basel) 9, 22. ( 10.3390/life9010022) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 6. Bellocchi G, Rivington M, Donatelli M, Matthews K. 2010. Validation of biophysical models: issues and methodologies. A review. Agron. Sust. Dev. 30, 109-130. ( 10.1051/agro/2009001) [ DOI ] [ Google Scholar ]
• 7. Costa E, Pérez J, Kreft JU. 2006. Why is metabolic labour divided in nitrification? Trends Microbiol. 14, 213-219. ( 10.1016/j.tim.2006.03.006) [ DOI ] [ PubMed ] [ Google Scholar ]
• 8. Daims H, et al. 2015. Complete nitrification by Nitrospira bacteria. Nature 528, 504-509. ( 10.1038/nature16461) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 9. Kissel JC, McCarty PL, Street RL. 1984. Numerical simulation of mixed-culture biofilm. J. Environ. Eng. 110, 393-411. [ Google Scholar ]
• 10. Henze M, Gujer W, Mino T, Van Loosdrecht MCM. 2002. Activated sludge models ASM1, ASM2, ASM2d and ASM3. London, UK: IWA Publishing. [ Google Scholar ]
• 11. Otuzalti MM, Perendeci NA. 2018. Modeling of real scale waste activated sludge anaerobic digestion process by Anaerobic Digestion Model 1 (ADM1). Int. J. Green Energy 15, 454-464. ( 10.1080/15435075.2018.1479265) [ DOI ] [ Google Scholar ]
• 12. Hellweger FL. 2017. 75 years since Monod: it is time to increase the complexity of our predictive ecosystem models (opinion). Ecol. Modell. 346, 77-87. ( 10.1016/j.ecolmodel.2016.12.001) [ DOI ] [ Google Scholar ]
• 13. Karimian E, Motamedian E. 2020. ACBM: an integrated agent and constraint based modeling framework for simulation of microbial communities. Sci. Rep. 10, 8695. ( 10.1038/s41598-020-65659-w) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 14. Cusick JA, Wellman CL, Demas GE. 2021. The call of the wild: using non-model systems to investigate microbiome–behaviour relationships. J. Exp. Biol. 224, jeb224485. ( 10.1242/jeb.224485) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 15. Kleerebezem R, Van Loosdrecht MCM. 2010. A generalized method for thermodynamic state analysis of environmental systems. Crit. Rev. Environ. Sci. Technol. 40, 1-54. ( 10.1080/10643380802000974) [ DOI ] [ Google Scholar ]
• 16. Sharma S, Steuer R. 2019. Modelling microbial communities using biochemical resource allocation analysis. J. R. Soc. Interface 16, 20190474. ( 10.1098/rsif.2019.0474) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 17. van den Berg NI, Machado D, Santos S, Rocha I, Chacón J, Harcombe W, Mitri S, Patil KR. 2022. Ecological modelling approaches for predicting emergent properties in microbial communities. Nat. Ecol. Evol. 6, 855-865. ( 10.1038/s41559-022-01746-7) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 18. Kreft JU, Griffin BM, Gonzalez-Cabaleiro R. 2020. Evolutionary causes and consequences of metabolic division of labour: why anaerobes do and aerobes don't. Curr. Opin. Biotechnol. 62, 80-87. ( 10.1016/j.copbio.2019.08.008) [ DOI ] [ PubMed ] [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

• View on publisher site
• PDF (686.5 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Between Theory and Phenomena: What are Scientific Models?

• First Online: 20 December 2015

Cite this chapter

• Axel Gelfert 2  

Part of the book series: SpringerBriefs in Philosophy ((BRIEFSPHILOSOPH))

1031 Accesses

Models are used across all scientific disciplines and come in a variety of different forms and shapes: as phenomenological models, theoretical models, mathematical models, toy models, scale models, etc. This bewildering array of different types of models naturally gives rise to the ontological question ‘What is a model?’, which the present chapter sets out to answer. The genealogy of scientific models can be traced back to the use of mechanical analogies in 19 th -century physics, and the first part of this chapter reviews some of the historical debates between, amongst others, Pierre Duhem and Norman R. Campbell. This is followed by a critical summary of the syntactic and semantic views of theories and models, which dominated 20 th -century philosophy of science, and by a discussion of the more recent proposal that models are best thought of as fictions. The final section discusses how a shift in attention, from questions of how science can be formalized to questions of scientific practice, poses a challenge also to traditional accounts of scientific models.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Suárez’s edited volume Fictions in Science [ 36 ] has recently sparked renewed interest in fictionalism about scientific models in particular.

For a discussion of inconsistent modeling assumptions, not only in the application but also in the construction of models, see [ 44 ].

For one such defence, see [ 50 ].

In Sect. 5.5 , I shall discuss in detail how some scientific models enable us to gain knowledge by functioning as mediators between different types of user–model–target relations, specifically between ‘embodied’ ways of relating to the world and those that require more specialized interpretive activities (such as ‘reading’ an instrument or manipulating a set of mathematical equations).

J. von Neumann, Method in the physical sciences, in Collected Works. Theory of Games, Astrophysics, Hydrodynamics and Meteorology , vol. VI, ed. by A.H. Taub (Pergamon Press, Oxford, 1961), pp. 491–498

Google Scholar  

R. Frigg, Models in science, Stanford encyclopedia of philosophy (2012). plato.stanford.edu/entries/models-science/ . Accessed 10 Feb 2015

N. Goodman, Languages of Art (Bobbs-Merrill, Indianapolis, 1968)

R. Ankeny, S. Leonelli, What’s so special about model organisms? Stud. Hist. Philos. Sci. 42 (2), 313–323 (2011)

Article   Google Scholar  

M. Black, Models and Metaphors: Studies in Language and Philosophy (Cornell University Press, Ithaca, 1962)

P. Achinstein, Concepts of Science: A Philosophical Analysis (Johns Hopkins Press, Baltimore, 1968)

B. Mahr, On the Epistemology of Models, in Rethinking Epistemology , vol. 1, ed. by G. Abel, J. Conant (de Gruyter, Berlin, 2012), pp. 301–352

G. Contessa, Editorial introduction to special issue. Synthese 172 (2), 193–195 (2010)

S. Ducheyne, Towards an Ontology of Scientific Models. Metaphysica 9 (1), 119–127 (2008)

R. Giere, Using Models to Represent Reality, in Model-based Reasoning in Scientific Discovery , ed. by L. Magnani, N. Nersessian, P. Thagard (Plenum Publishers, New York, 1999), pp. 41–57

Chapter   Google Scholar  

A. Chakravartty, Informational versus functional theories of scientific representation. Synthese 172 (2), 197–213 (2010)

P. Duhem, The Aim and Structure of Physical Theory . Transl. P.P. Wiener (Princeton University Press, Princeton, 1914/1954)

D. Bailer-Jones, Models, Metaphors and Analogies, in The Blackwell Guide to the Philosophy of Science , ed. by P. Machamer, M. Silberstein (Blackwell, Oxford, 2002), pp. 108–127

D.H. Mellor, Models and analogies in science: Duhem versus Campbell? Isis 59 (3), 282–290 (1968)

D. Bailer-Jones, Scientific Models in Philosophy of Science (University of Pittsburgh Press, Pittsburgh, 2009)

M. Hesse, Models and Analogies in Science (Sheed and Ward, London, 1963)

N.R. Campbell, Physics: The Elements (Cambridge University Press, Cambridge, 1920/2013)

J.M. Soskice, R. Harré, Metaphor in Science, in From a Metaphorical Point of View: A Multidisciplinary Approach to the Cognitive Content of Metaphor , ed. by Z. Radman (de Gruyter, Berlin, 1995), pp. 289–308

R. Carnap, Foundations of Logic and Mathematics (The University of Chicago Press, Chicago, 1939)

R.F. Hendry, S. Psillos, How to Do Things with Theories: An Interactive View of Language and Models in Science, in The Courage of Doing Philosophy: Essays Presented to Leszek Nowak , ed. by J. Brzeziński, A. Klawiter, T.A.F. Kuipers, K. Lastowski, K. Paprzycka, P. Przybyzs (Rodopi, Amsterdam, 2007), pp. 123–158

R. Carnap, Foundations of Logic and Mathematics, in Foundations of the Unity of Science , vol. 1, ed. by O. Neurath, R. Carnap, C. Morris (The University of Chicago Press, Chicago, 1969), pp. 139–214

R.B. Braithwaite, Scientific Explanation: A Study of the Function of Theory, Probability and Law in Science (Cambridge University Press, Cambridge, 1968)

N. Cartwright, Models and the Limits of Theory: Quantum Hamiltonians and the BCS Model of Superconductivity, in Models as Mediators: Perspectives on Natural and Social Science , ed. by M.S. Morgan, M. Morrison (Cambridge University Press, Cambridge, 1999), pp. 241–281

F. Suppe, The Semantic Conception of Theories and Scientific Realism (University of Illinois Press, Urbana, 1989)

P. Suppes, A Comparison of the Meaning and Uses of Models in Mathematics and the Empirical Sciences. Synthese 12 (2–3), 287–301 (1960)

B. van Fraassen, The Scientific Image (Oxford University Press, Oxford, 1980)

Book   Google Scholar  

C. Liu, Models and theories I: the semantic view revisited. Int. Stud. Philos. Sci. 11 (2), 147–164 (1997)

M. Thomson-Jones, Models and the semantic view. Philos. Sci. 73 (5), 524–535 (2006)

P. Suppes, Introduction to Logic (Van Nostrand, Princeton, 1957)

A. Gelfert, Mathematical formalisms in scientific practice: from denotation to model-based representation. Stud. Hist. Philos. Sci. 42 (2), 272–286 (2011)

P. Godfrey-Smith, The strategy of model-based science. Biol. Philos. 21 (5), 725–740 (2006)

M. Thomson-Jones, Missing systems and the face value practice. Synthese 172 (2), 283–299 (2010)

M. Wartofsky, Models, Metaphysics and the Vagaries of Empiricism, in Models: Representation and the Scientific Understanding (Reidel, Dordrecht, 1979), pp. 24–39

N. Cartwright, How the Laws of Physics Lie (Oxford University Press, Oxford, 1983)

M. Suárez, Scientific Fictions as Rules of Inference, in Fictions in Science: Philosophical Essays on Modeling and Idealization , ed. by M. Suárez (Routledge, London, 2009), pp. 158–178

M. Suárez, Fictions in Science: Philosophical Essays on Modeling and Idealization , ed. by M. Suárez (Routledge, London, 2009)

R. Frigg, Models and fiction. Synthese 172 (2), 251–268 (2010)

K. Walton, Mimesis as Make-Believe: On the Foundations of the Representational Arts (Harvard University Press, Cambridge, Mass., 1990)

A. Toon, Models as Make-Believe: Imagination, Fiction, and Scientific Representation (Palgrave-Macmillan, Basingstoke, 2012)

A. Toon, The ontology of theoretical modelling: models as make-believe. Synthese 172 (2), 301–315 (2010)

H.G. Wells, War of the Worlds (Penguin, London, 1897/1978)

R. Giere, How models are used to represent reality. Philos. Sci. 71 (5), S742–S752 (2004)

T.S. Kuhn, The Structure of Scientific Revolutions (The University of Chicago Press, Chicago, 1962)

M. Frisch, Models and scientific representations or: who is afraid of inconsistency? Synthese 191 (13), 3027–3040 (2014)

S.M. Downes, The Importance of Models in Theorizing: A Deflationary Semantic View . Proceedings of the PSA1992, vol. 1, Chicago, 1992

N. da Costa, S. French, Science and Partial Truth: A Unitary Approach to Models and Scientific Reasoning (Oxford University Press, New York, 2003)

S. French, The structure of theories, in The Routledge Companion to Philosophy of Science , 2nd edn., ed. by M. Curd, S. Psillos (Routledge, London, 2013), pp. 301–312

C. Pincock, Overextending partial structures: idealization and abstraction. Philos. Sci. 72 (5), 1248–1259 (2005)

M. Suárez, N. Cartwright, Theories: tools versus models. Stud. Hist. Philos. Mod. Phys. 39 (1), 62–81 (2008)

S. French, J. Ladyman, Reinflating the semantic approach. Int. Stud. Philos. Sci. 13 (2), 103–121 (1999)

U. Mäki, MISSing the world. Models as isolations and credible surrogate systems. Erkenntnis 70 (1), 29–43 (2009)

M. Morrison, M. Morgan, Models as Mediating Instruments, in Models as Mediators: Perspectives on Natural and Social Science , ed. by M.S. Morgan, M. Morrison (Cambridge University Press, Cambridge, 1999), pp. 10–37

T. Knuuttila, Models as Epistemic Artefacts: Toward a Non-Representationalist Account of Scientific Representation (University of Helsinki, Helsinki, 2005)

T. Knuuttila, Modelling and representing: an artefactual approach to model-based representation. Stud. Hist. Philos. Sci. 42 (2), 262–271 (2011)

Download references

Author information

Authors and affiliations.

Department of Philosophy, National University of Singapore, Singapore, Singapore

Axel Gelfert

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Axel Gelfert .

Rights and permissions

Reprints and permissions

Copyright information

© 2016 The Author(s)

About this chapter

Gelfert, A. (2016). Between Theory and Phenomena: What are Scientific Models?. In: How to Do Science with Models. SpringerBriefs in Philosophy. Springer, Cham. https://doi.org/10.1007/978-3-319-27954-1_1

Download citation

DOI : https://doi.org/10.1007/978-3-319-27954-1_1

Published : 20 December 2015

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-27952-7

Online ISBN : 978-3-319-27954-1

eBook Packages : Religion and Philosophy Philosophy and Religion (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research