data science hypothesis testing

• Python for Data Science
• Data Analysis
• Machine Learning
• Deep Learning
• Deep Learning Interview Questions
• ML Projects
• ML Interview Questions

Understanding Hypothesis Testing

Hypothesis testing is a fundamental statistical method employed in various fields, including data science , machine learning , and statistics , to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously evaluating these assumptions against collected data. At its core, hypothesis testing is a systematic approach that allows researchers to assess the validity of a statistical claim about an unknown population parameter. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

Table of Content

What is Hypothesis Testing?

Why do we use hypothesis testing, one-tailed and two-tailed test, what are type 1 and type 2 errors in hypothesis testing, how does hypothesis testing work, real life examples of hypothesis testing, limitations of hypothesis testing.

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

To test the validity of the claim or assumption about the population parameter:

• A sample is drawn from the population and analyzed.
• The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

This structured approach to hypothesis testing in data science , hypothesis testing in machine learning , and hypothesis testing in statistics is crucial for making informed decisions based on data.

• By employing hypothesis testing in data analytics and other fields, practitioners can rigorously evaluate their assumptions and derive meaningful insights from their analyses.
• Understanding hypothesis generation and testing is also essential for effectively implementing statistical hypothesis testing in various applications.

Defining Hypotheses

• Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
• Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis.  Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.

Key Terms of Hypothesis Testing

• Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with  [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

Understanding hypothesis testing in statistics is essential for data scientists and machine learning practitioners, as it provides a structured framework for statistical hypothesis generation and testing. This methodology can also be applied in hypothesis testing in Python , enabling data analysts to perform robust statistical analyses efficiently. By employing techniques such as multiple hypothesis testing in machine learning , researchers can ensure more reliable results and avoid potential pitfalls associated with drawing conclusions from statistical tests. 

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

• Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 ​: [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
• Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]

To delve deeper into differences into both types of test: Refer to link

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

• Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
• Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).

Step 1: Define Null and Alternative Hypothesis

State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ​), suggesting an effect or difference.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

• If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
• If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]

• [Tex]\bar{x} [/Tex] is the sample mean,
• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]

• [Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
• i,j are the rows and columns index respectively.
• [Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] ​ and we get accordingly , Z =2.039999999999992.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.

Although hypothesis testing is a useful technique in data science , it does not offer a comprehensive grasp of the topic being studied.

• Lack of Comprehensive Insight : Hypothesis testing in data science often focuses on specific hypotheses, which may not fully capture the complexity of the phenomena being studied.
• Dependence on Data Quality : The accuracy of hypothesis testing results relies heavily on the quality of available data. Inaccurate data can lead to incorrect conclusions, particularly in hypothesis testing in machine learning .
• Overlooking Patterns : Sole reliance on hypothesis testing can result in the omission of significant patterns or relationships in the data that are not captured by the tested hypotheses.
• Contextual Limitations : Hypothesis testing in statistics may not reflect the broader context, leading to oversimplification of results.
• Complementary Methods Needed : To gain a more holistic understanding, it’s essential to complement hypothesis testing with other analytical approaches, especially in data analytics and data mining .
• Misinterpretation Risks : Poorly formulated hypotheses or inappropriate statistical methods can lead to misinterpretation, emphasizing the need for careful consideration in hypothesis testing in Python and related analyses.
• Multiple Hypothesis Testing Challenges : Multiple hypothesis testing in machine learning poses additional challenges, as it can increase the likelihood of Type I errors, requiring adjustments to maintain validity.

Hypothesis testing is a cornerstone of statistical analysis , allowing data scientists to navigate uncertainties and draw credible inferences from sample data. By defining null and alternative hypotheses, selecting significance levels, and employing statistical tests, researchers can validate their assumptions effectively.

This article emphasizes the distinction between Type I and Type II errors, highlighting their relevance in hypothesis testing in data science and machine learning . A practical example involving a paired T-test to assess a new drug’s effect on blood pressure underscores the importance of statistical rigor in data-driven decision-making .

Ultimately, understanding hypothesis testing in statistics , alongside its applications in data mining , data analytics , and hypothesis testing in Python , enhances analytical frameworks and supports informed decision-making.

Understanding Hypothesis Testing- FAQs

What is hypothesis testing in data science.

In data science, hypothesis testing is used to validate assumptions or claims about data. It helps data scientists determine whether observed patterns are statistically significant or could have occurred by chance.

How does hypothesis testing work in machine learning?

In machine learning, hypothesis testing helps assess the effectiveness of models. For example, it can be used to compare the performance of different algorithms or to evaluate whether a new feature significantly improves a model’s accuracy.

What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

What is the difference between hypothesis testing and data mining?

Hypothesis testing focuses on evaluating specific claims or hypotheses about a dataset, while data mining involves exploring large datasets to discover patterns, relationships, or insights without predefined hypotheses.

How is hypothesis generation used in business analytics?

In business analytics , hypothesis generation involves formulating assumptions or predictions based on available data. These hypotheses can then be tested using statistical methods to inform decision-making and strategy.

What is the significance level in hypothesis testing?

The significance level, often denoted as alpha (α), is the threshold for deciding whether to reject the null hypothesis. Common significance levels are 0.05, 0.01, and 0.10, indicating the probability of making a Type I error in statistical hypothesis testing .

Similar Reads

• Data Science
• data-science

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Onsite training

3,000,000+ delegates

15,000+ clients

1,000+ locations

• KnowledgePass
• Log a ticket

01344203999 Available 24/7

Hypothesis Testing in Data Science: Its Usage and Types

Curious to know about Hypothesis Testing Data Science? Hypothesis Testing is a way of analysing the validity of claims or observations through a set of scientific and data-driven tests. Read this blog to explore Hypothesis Testing in Data Science, its importance, types, implementation steps, and use- cases, among others.

Exclusive 40% OFF

Training Outcomes Within Your Budget!

We ensure quality, budget-alignment, and timely delivery by our expert instructors.

Share this Resource

• Advanced Data Science Certification
• Data Science and Blockchain Training
• Big Data Analysis
• Python Data Science Course
• Advanced Data Analytics Course

How can you ensure the reliability of data-driven decisions in an environment riddled with misinformation? The answer lies in the Hypothesis Testing! Hypothesis testing is among the most significant topics in the field of data science. It helps Data Scientists analyse whether the observed effect is statistically correct or merely coincidental through a set of scientific and data-centred tests. This blog will delve deeper into what exactly Hypothesis Testing in Data Science is to help you understand its importance, types, steps to follow, and real-world use cases. Let’s embark on this data-embedded journey!

Table of Contents 

1) What is Hypothesis Testing in Data Science? 

2) Importance of Hypothesis Testing in Data Science 

3) Types of Hypothesis Testing 

4) Basic Steps in Hypothesis Testing 

5) Real-world Use Cases of hypothesis Testing 

6) Conclusion 

What is Hypothesis Testing in Data Science?  

Hypothesis Testing in Data Science is a statistical method used to assess the legitimacy of assumptions or claims made on the population on the basis of sample data. It involves formulating two Hypotheses, the Null Hypothesis (H0) and the alternative Hypothesis (H1, which can be termed antonyms to the Null Hypothesis), and then using the applications of statistical tests to find out if there is enough credible evidence to support the Alternative Hypothesis.    

For instance, you want to analyse whether plant food is effective. On the one hand, you assume that the plant will grow with that other food (termed as an alternative Hypothesis); on the other hand, you say that the plant will not grow (that’s a Null Hypothesis). So, to test the validity of the claims made, you perform specific scientific experiments and tests like adding that plant food into the soil for a few weeks to see if the plant grows.  

Importance of Hypothesis Testing in Data Science  

Hypothesis Testing in Data Science serves as the cornerstone of scientifical, data-driven decision-making. By systematically testing Hypotheses, Data Scientists can perform several tasks. Below, we have illustrated the importance of Hypothesis Testing. 

1) Objective Decision-making 

Hypothesis Testing provides a structured and impartial method for data professionals to make evidence-backed decisions based on efficient data analysis. In addition, in the uncertainties of biases-skewed results, Data Scientists predominantly use this method to make sure that their conclusions are grounded in empirical evidence, making their decisions more objective and trustworthy. 

2) Statistical Rigour 

Data Scientists deal with large datasets and Hypothesis Testing helps them make  meaningful sense of them. It quantifies the significance of observed patterns, differences, or relationships. This statistical rigour is critical for determining the differences between mere coincidences and meaningful findings, thus reducing the possibility of making decisions based on random chance. 

3) Resource Allocation 

Resources, irrespective of whether they are financial, human, or time-related, are often limited. Hypothesis Testing enables Data Scientists to allocate resources efficiently by allowing them to develop statistical strategies or interventions. This ensures that efforts are directed where they are most likely to yield valuable and meaningful results. 

4) Risk Management 

In domains including healthcare and finance, where you cannot determine the lives and livelihoods, Hypothesis Testing serves as an integral tool for risk assessment. For instance, in drug development, Hypothesis Testing can ascertain the safety and efficiency of new treatments, helping mitigate potential risks to patients. 

5) Innovation and Progress 

Hypothesis Testing promotes innovation by providing a systematic framework to evaluate and frame newer ideas, products, and strategies. It encourages continual experimentation, feedback, and improvement, ultimately driving continuous progress and innovation.

6) Strategic Decision-making 

Organisations formulate their strategies based on data-driven insights. Hypothesis Testing enables them to make informed decisions about market trends, customer behaviour, and product development. These decisions have a foundational basis in empirical evidence, which increases the likelihood of success.  

7) Scientific Integrity 

In scientific research, Hypothesis Testing is integral to maintaining the integrity of research findings. It ensures accurate conclusions are drawn from rigorous statistical analysis rather than  supposition. This robustness is essential for advancing knowledge and on the basis of the existing research. 

8) Regulatory Compliance 

Several industries ranging from pharmaceuticals to aviation, work under strict regulatory frameworks. Hypothesis Testing helps them to ensure those frameworks comply with the necessary safety and quality standards. 

Master Probability for Data Science with our Probability and Statistics for Data Science Training – join now!

Types of Hypothesis Testing  

There are several types of Hypothesis Testing, such as null, alternative, one-tailed, and two-tailed tests. These types are described as follows:

1) Alternative Hypothesis

The Alternative Hypothesis, denoted as Ha or H1, is the assertion or claim that researchers make to support their data analysis. The main goal of the Alternative Hypothesis is to suggest that there is a significant effect, relationship, or difference in the population. To put it in simpler words, it's the statement that researchers hope to find evidence for during their analysis. For example, if you are testing a new drug's efficacy, the Alternative Hypothesis might state that the drug has a measurable positive effect on patients' health. 

2) Null Hypothesis  

The Null Hypothesis, denoted as H0, is the standardised assumption in Hypothesis Testing. It defines that there is no significant effect, relationship, or difference in the observing population. In other words, it represents the status quo or the absence of an effect. Researchers typically collect and analyse enough data to challenge or disapprove of the Null Hypothesis. Considering the drug efficacy example again, the Null Hypothesis might state that the new drug has no effect on patients' health.  

3) Non-directional Hypothesis 

A Non-directional Hypothesis, also known as a two-tailed Hypothesis, is used when researchers are interested to know if there is any significant difference, effect, or relationship without taking into account its direction of impact (positive or negative). This type of Hypothesis allows the possibility of finding impacts in bi-directions (both positive and negative sides). For instance, in a study comparing the performance of two groups, a Non-directional Hypothesis would suggest that there is a significant difference between the groups without specifying which group performs better. 

4) Directional Hypothesis 

A Directional Hypothesis, also called a one-tailed Hypothesis, is employed when researchers have a specific expectation about the direction of the impact, relationship, or difference they are investigating. In this case, the Hypothesis predicts an outcome in a particular direction—either positive or negative. For example, if you expect a new teaching method to improve student test scores, a directional Hypothesis will state that the new method leads to higher test scores. 

5) Statistical Hypothesis 

A Statistical Hypothesis is a specific statement about a population parameter made on the basis of the statistical-based tests. It involves specific numerical values or parameters that can be measured or compared. Such types of hypotheses are crucial for quantitative research and often include means, proportions, variances, correlations, or other measurable quantities. As a result, they provide a precise framework for conducting statistical tests and drawing inferences based on data analysis. 

Sharpen your Predictive Modeling techniques with our Predictive Analytics Course - register today!

Basic Steps in Hypothesis Testing  

Hypothesis Testing is a critical tool in Data Science, research, and several other fields where data analysis is employed. The following are the basic steps involved in Hypothesis Testing: 

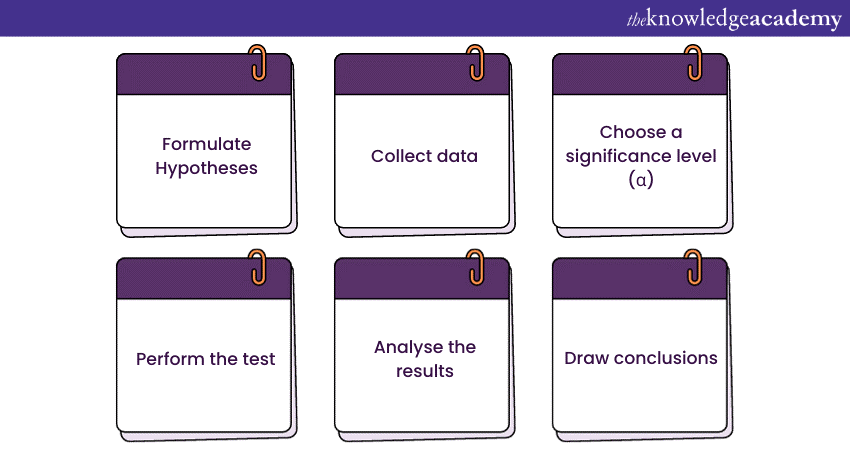
1) Formulate Hypotheses 

The first step in Hypothesis Testing is to clearly define your research question and convert it into two mutually exclusive Hypotheses: 

a) Null Hypothesis (H0): This is the default assumption, often representing the status quo or the absence of an effect. It states that there is no significant difference, relationship, or effect in the population. 

b) Alternative Hypothesis (Ha or H1): This is the statement that contradicts the null Hypothesis. It suggests that there is a significant difference, relationship, or effect in the population. 

This Hypotheses formulation is crucial, as they serve as the foundation for your entire Hypothesis Testing process. 

2) Collect Data 

The next step is to gather relevant data by performing various types of surveys, experiments, observations, or any other related methods. You must ensure that the sample data collected should be represent the entire population where you are studying.

3) Choose a Significance Level (α) 

Before conducting the statistical test, you need to assess the significance level, which is denoted as ‘α’. The significance level represents the threshold for statistical significance and ascertains your confidence in your results. A common choice is α = 0.05, which implies a 5% risk of making a Type I error (rejecting the Null Hypothesis when it's true). You can choose a different ‘α’ value based on the specific requirements of your analysis. 

4) Perform the Test 

Based on your formulated data and Hypotheses, select the appropriate statistical test. To this, there are various tests available, including t-tests, chi-squared tests, ANOVA, Regression Analysis, and more. You need to ensure the chosen test aligns with the data type (e.g., continuous or categorical) and the research question (e.g., comparing means or testing for independence). 

Execute the selected statistical test on your data to obtain test statistics and p-values. The test statistics quantify your investigating difference or effect, while the p-value represents the probability of obtaining the observed results if the null Hypothesis were true. 

5) Analyse the Results 

Once you have the test statistics and p-value, it's time to interpret the results. The primary focus in this case is on the p-value: 

a) If the p-value is less than or equal to your chosen significance level (α), typically 0.05, you have evidence to reject the null Hypothesis. This shows that there is a significant difference, relationship, or effect in the population to support the alternative Hypothesis.

b) If the p-value is more than α, you fail to reject the null Hypothesis. This shows that there is insufficient evidence to support the alternative Hypothesis. 

6) Draw Conclusions  

Based on the analysis of the p-value and comparing it with the significance level (α), you can draw conclusions about your research question: 

a) In case you reject the null Hypothesis, you can accept the alternative Hypothesis and make inferences based on the evidence provided by your data. 

b) In case you fail to reject the null Hypothesis, do not accept the alternative Hypothesis, and you acknowledge that there is no significant evidence to support your claim. 

Real-world Use Cases of Hypothesis Testing  

Hypothesis testing is a crucial facet of reducing the uncertainty of our lives. The following are some of the real-world use cases of Hypothesis Testing. 

a) Medical Research: Hypothesis Testing is crucial for medical researchers to analyse the efficacy of new medications or treatments. For instance, researchers use Hypothesis Testing in a clinical trial to assess whether a new drug is more effective than a placebo in treating a particular condition or not.  

b) Marketing and Advertising: Businesses use Hypothesis Testing to evaluate the effectiveness of marketing campaigns. A company may test whether a new advertising strategy can lead to a significant increase in sales compared to the previous approach. 

c) Manufacturing and Quality Control: Manufacturing industries use the application of Hypothesis Testing to ensure the optimum quality of their products. For example, in the automotive industry, Hypothesis Testing can be applied to test to assess whether a new manufacturing process can reduce the arising defects in an automobile engine. 

d) Education: In the field of education, Hypothesis Testing can be used to assess the effectiveness of teaching methods. Researchers may test whether a new teaching approach can lead to statistically significant improvements in student performance. 

e) Finance and Investment: Investment strategies are often evaluated using Hypothesis Testing. Investors may need to test whether a new investment strategy outperforms a benchmark index over a specified period.

Discover patterns with advanced algorithms- join our Data Mining Training today!

We hope you understand Hypothesis Testing in Data Science.  Hypothesis Testing is a powerful tool that enables Data Scientists to make evidence-based decisions and draw meaningful conclusions and valuable inferences from larger datasets. Understanding its types, methods, and steps involved in Hypothesis Testing is crucial for any Data Scientist to make transparent and data-driven decisions based on scientific evidence. By tactically applying Hypothesis Testing techniques mentioned in this blog, you can gain valuable insights and drive informed decision-making in numerous domains, ranging from technology and finance to the medical industry. 

Build robust models with R Techniques with our Decision Tree Modeling Using R Training - join now!

Frequently Asked Questions

To calculate the sample size for Hypothesis Testing, you need to assess the effect size, significance level (α), power (1 - β), and variability (standard deviation). Then, by applying the sample size formulas that align with your test (e.g., t-test), you can find the exact sample size to simplify your data analytics.  

If Hypothesis Testing assumptions are violated, you should try to transform your data using non-parametric tests or applying several robust statistical methods. Otherwise, you can increase the sample size for accurate solutions. Moreover, it's important to determine which specific assumptions are violated to select the most appropriate method. 

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide. 

Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs , videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA .   

The Knowledge Academy’s Knowledge Pass , a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds. 

The Knowledge Academy offers various Data Science Courses , including Probability and Statistics for Data Science Training, Predictive Analytics Course, and Advanced Data Science Certification. These courses cater to different skill levels, providing comprehensive insights into All You Need to Know about Statistical Analysis in Data Science .

Our Data, Analytics & AI Blogs cover a range of topics related to Data Science and machine learning, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your analytical and technical skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.  

Upcoming Data, Analytics & AI Resources Batches & Dates

Fri 21st Feb 2025

Fri 25th Apr 2025

Fri 20th Jun 2025

Fri 22nd Aug 2025

Fri 17th Oct 2025

Fri 19th Dec 2025

Get A Quote

WHO WILL BE FUNDING THE COURSE?

My employer

By submitting your details you agree to be contacted in order to respond to your enquiry

• Business Analysis
• Lean Six Sigma Certification

Share this course

Biggest black friday sale.

We cannot process your enquiry without contacting you, please tick to confirm your consent to us for contacting you about your enquiry.

By submitting your details you agree to be contacted in order to respond to your enquiry.

We may not have the course you’re looking for. If you enquire or give us a call on 01344203999 and speak to our training experts, we may still be able to help with your training requirements.

Or select from our popular topics

• ITIL® Certification
• Scrum Certification
• ISO 9001 Certification
• Change Management Certification
• Microsoft Azure Certification
• Microsoft Excel Courses
• Explore more courses

Press esc to close

Fill out your  contact details  below and our training experts will be in touch.

Fill out your   contact details   below

Thank you for your enquiry!

One of our training experts will be in touch shortly to go over your training requirements.

Back to Course Information

Fill out your contact details below so we can get in touch with you regarding your training requirements.

* WHO WILL BE FUNDING THE COURSE?

Preferred Contact Method

No preference

Back to course information

Fill out your  training details  below

Fill out your training details below so we have a better idea of what your training requirements are.

HOW MANY DELEGATES NEED TRAINING?

HOW DO YOU WANT THE COURSE DELIVERED?

Online Instructor-led

Online Self-paced

WHEN WOULD YOU LIKE TO TAKE THIS COURSE?

Next 2 - 4 months

WHAT IS YOUR REASON FOR ENQUIRING?

Looking for some information

Looking for a discount

I want to book but have questions

One of our training experts will be in touch shortly to go overy your training requirements.

Your privacy & cookies!

Like many websites we use cookies. We care about your data and experience, so to give you the best possible experience using our site, we store a very limited amount of your data. Continuing to use this site or clicking “Accept & close” means that you agree to our use of cookies. Learn more about our privacy policy and cookie policy cookie policy .

We use cookies that are essential for our site to work. Please visit our cookie policy for more information. To accept all cookies click 'Accept & close'.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

• We first choose a significance level ($α$), which sets a threshold for making decisions.

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

• --> Statistics -->

--> F Statistic Formula – Explained -->

--> correlation – connecting the dots, the role of correlation in data analysis -->, --> hypothesis testing – a deep dive into hypothesis testing, the backbone of statistical inference -->, --> sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions -->, --> law of large numbers – a deep dive into the world of statistics -->, --> central limit theorem – a deep dive into central limit theorem and its significance in statistics -->, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Hypothesis Testing in Data Science

Statistics is a branch of mathematics discipline that is related to the collection, analysis, interpretation, and presentation of data. Statistics is a powerful tool for understanding, interpreting data, and making informed decisions.

Hypothesis Testing is one of the most important concepts in Statistics. In Statistics, Hypothesis Testing is to ascertain whether a hypothesis about a population is true. Let’s explore Hypothesis Testing in detail in this article.

What is Hypothesis Testing?

• Formulate a specific assumption or hypothesis about a larger population.
• Collect data from a sample of the population.
• Use various statistical methods to determine whether the data supports the hypothesis or not.
• Hypothesis Testing allows Data Scientists and Analysts to derive inferences about a population based on the data collected from a sample, and to determine whether their initial assumptions or hypotheses were correct.
• Null Hypothesis: The Null Hypothesis assumes no significant relationship exists between the variables being studied (one variable does not affect the other). In other words, it assumes that any observed effects in the sample are due to chance and are not real. The Null Hypothesis is typically denoted as H0 .
• Alternative Hypothesis: It is the opposite of the Null Hypothesis. It assumes that there is a significant relationship between the variables. In other words, it assumes that the observed effects in the sample are real and are not due to chance. The Alternative Hypothesis is typically denoted as H1 or Ha .
• Hypothesis Testing is used to test a new drug's effectiveness in treating a certain disease. In this case, the Null Hypothesis will be that the drug is not effective at treating the disease, and the Alternative Hypothesis will be that the drug is effective.
• It is also used to ascertain the effectiveness of a marketing campaign. In this case, the Null Hypothesis will be that the marketing campaign has no effect on sales and revenue, and the Alternative Hypothesis will be that the campaign is effective at increasing sales.
• Various statistical methods are further used to reject or fail to reject the Null Hypothesis.

Significance Level and P-Value

Significance level.

• The significance level is a probability threshold used in hypothesis testing to determine whether a study's results are statistically significant.
• It is essentially the probability threshold of the case when we reject the null hypothesis, but in reality, it is true. For example, a 0.05 significance level means that the probability of observing data/results must be less than 0.05 for the results to be statistically significant. It is denoted by alpha (α) .
• Generally, the lower the significance level, the more stringent the criteria for determining statistical significance.
• A p-value , or probability value , describes the likelihood of the occurrence of the observed data by random chance (Null Hypothesis is true).
• For example, suppose the statistical significance is set at 0.05 and the p-value of the results is less than 0.05 . In that case, the results are considered statistically significant, and the null hypothesis is rejected. If the p-value > 0.05 , then we can not reject the null hypothesis.

Comparison of Means

• Comparison of Means is a method that is used to determine whether the means of two or more groups are significantly different from each other or not. It is used to determine whether the observed difference between two means is due to chance or not.
• In this test, the null hypothesis is that there is no difference between the two means, and the alternative hypothesis is that the two means are significantly different.
• Several tests, such as z-test, t-test, ANOVA , etc., are used to perform this method.

Z-Test is used to compare the means of two groups when the population's standard deviation is known, and the number of samples is large.

It is calculated by dividing the difference between the two means by the standard error of the mean. The resulting z-score is then compared to a normal distribution to determine whether the difference is statistically significant or not.

Z-score for two groups (sample and population) can be calculated using the below formula:

The T-Test is similar to z-tests, but they are used when the populations’ standard deviation is unknown and the number of samples is small ( n &lt;= 30 ).

The t-test calculates the difference between the two means and compares it to a t-distribution to determine whether the difference is statistically significant.

There are several types of t-tests used to compare the means of two groups, such as one-sample t-test, two-sample t-test, independent sample t-test , etc.

The formula to calculate t-test statistic is shown below, where x ˉ \bar x x ˉ is the mean of the sample, μ \mu μ is the mean of the population, σ \sigma σ is the standard deviation, and n n n is the total number of observations in the sample.

Test of Proportions

• A test of proportions is used to compare the proportion/percentage of individuals in two groups exhibiting a certain characteristic. This method is useful to determine whether the proportions of individuals in a sample differ significantly with a larger population.
• For example, the test of proportions can be used to compare the proportion/percentage of males and females with a certain medical condition, it can be used to compare the percentage of genders in newborn babies, etc. A test of proportions aims to determine whether the observed differences in the ratios are significant or if they are simply due to chance.
• In Data Science , tests of proportions can be used to compare two variables when one variable is categorical and the other is numerical. Several techniques are used to perform proportions tests, such as the chi-square goodness of fit test, one proportion z-test , two proportion z-test , etc.

Chi-Square Goodness of Fit Test

In the Chi-Square Goodness of Fit Test , we evaluate whether the proportions of a categorical variable in the sample follow the population distribution with hypothesized proportions.

The null and alternative hypotheses in the chi-square goodness of fit test are defined as follows:

• Null Hypothesis: The sample data follow the population distribution with the hypothesized distribution.
• Alternative Hypothesis: The sample data do not follow the population distribution with the hypothesized distribution.

The formula for the chi-squared goodness of fit test is shown O is the observed frequency for each category, and E is the expected frequency for each category under the hypothesized distribution.

The resulting chi-squared statistic is then compared to a critical value from a chi-squared distribution table to determine the p-value.

The null hypothesis is rejected if the p-value is less than the predetermined significance level (usually 0.05 ).

Test of Independence

• The test of independence is a statistical method that is used to determine whether there is any association or correlation between two categorical variables or whether both variables are independent of each other.
• The chi-squared test of independence is one of the most popular methods to perform the test of independence.

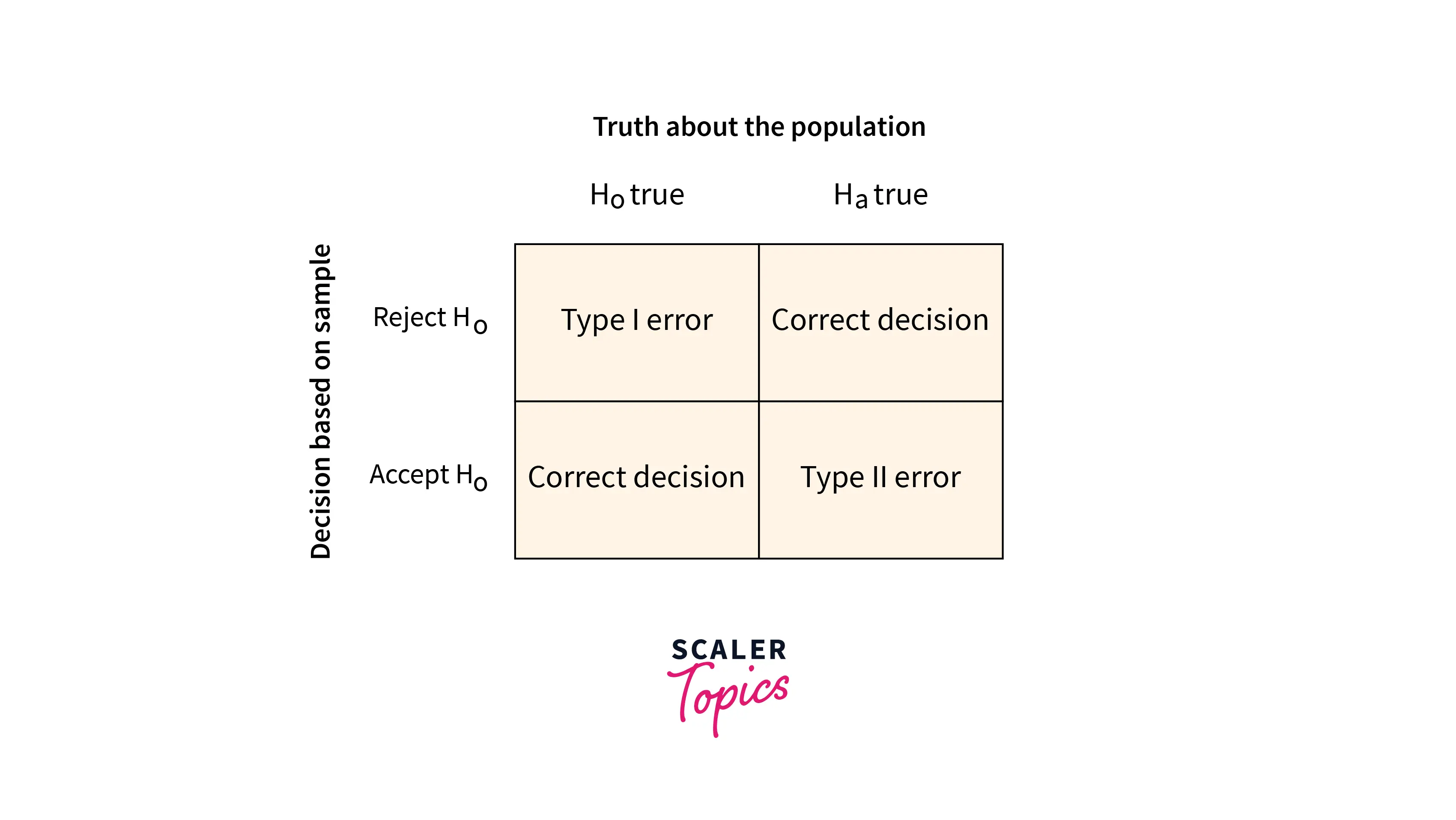
Type I and Type II Error

During performing Hypothesis Testing, there might be some errors. Two types of errors are generally encountered while performing Hypothesis Testing.

• Type I Error: Type I error is the case when we reject the null hypothesis, but in reality, it is true. The probability of having a Type-I error is called significance level alpha(α) . It is the case of False Positive or incorrect rejection of the null hypothesis.
• Type II Error: Type II error is the case when we fail to reject the null hypothesis, but it is false. The probability of having a type-II error is called beta(β) . It is the case of False Negative or incorrect acceptance of the null hypothesis.

ANOVA stands for Analysis of Variance . In statistics, the ANOVA test is generally used to determine whether multiple groups have statistically significant different means or not.

This method is advantageous for comparing the means of groups when you have more than two groups to study. T-tests on multiple groups result in a higher error rate, while ANOVA keeps it lower.

Below are the steps to perform the ANOVA test to compare the means of multiple groups:

• Hypothesis Generation
• Calculate within the group and between groups variability and other metrics
• Calculate F-Ratio
• Calculate probability (p-value) by comparing F-Ration to F-table
• Use p-value to reject/fail to reject the null hypothesis

ANOVA test can be performed using the formulas mentioned below figure:

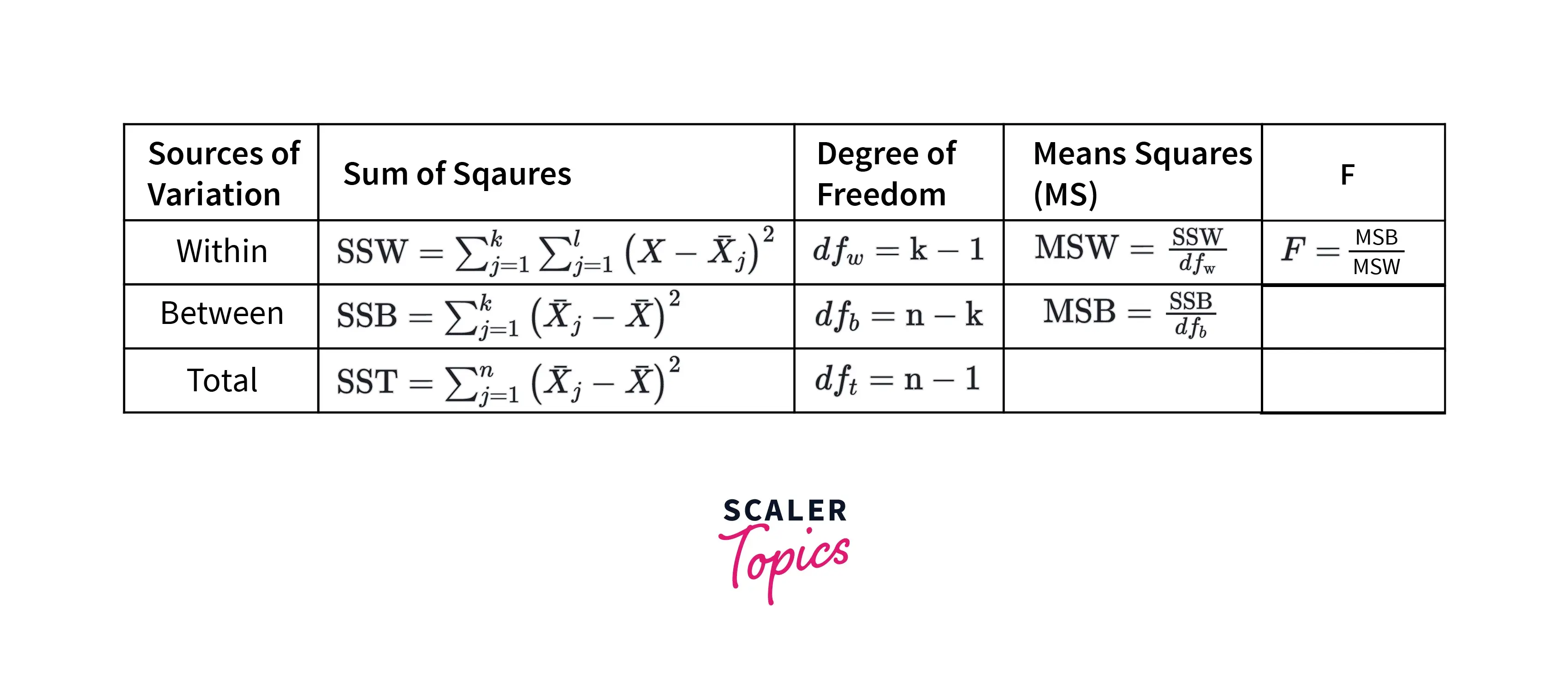
• The Sum of Squares is the squared mean differences between groups and within the group.
• For between groups, the degree of freedom is defined as k − 1 k-1 k − 1 , where k is the total number of groups to study. For within groups, it is n − k n-k n − k , where n is the total observations.
• Hypothesis Testing is used to determine whether a certain set of hypotheses about a larger population is true or not.
• In Data Science, it is frequently used to compare two variables, whether they are statistically significant or independent of each other. A few of the most common methods to perform Hypothesis Testing include - the z-test, t-test, chi-squared test, ANOVA , etc.