problem solving learning in psychology

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

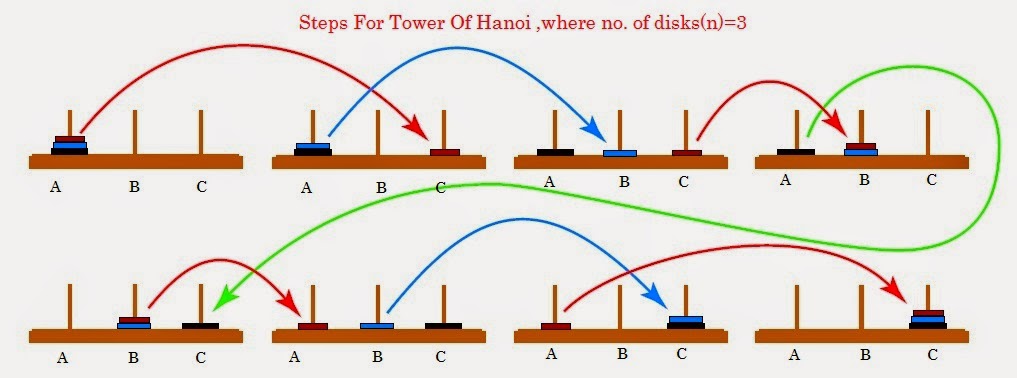
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

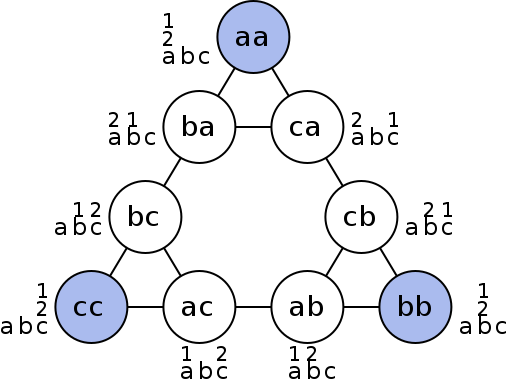
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

9 Chapter 9. Problem-Solving

CHAPTER 9: PROBLEM SOLVING  

How do we achieve our goals when the solution is not immediately obvious? What mental blocks are likely to get in our way, and how can we leverage our prior knowledge to solve novel problems?

CHAPTER 9 LICENSE AND ATTRIBUTION

Source: Multiple authors. Memory. In Cognitive Psychology and Cognitive Neuroscience. Wikibooks. Retrieved from https://en.wikibooks.org/wiki/ Cognitive_Psychology_and_Cognitive_Neuroscience

Wikibooks are licensed under the Creative Commons Attribution-ShareAlike License.

Cognitive Psychology and Cognitive Neuroscience is licensed under the GNU Free Documentation License.

Condensed from original version. American spellings used. Content added or changed to reflect American perspective and references. Context and transitions added throughout. Substantially edited, adapted, and (in some parts) rewritten for clarity and course relevance.

Cover photo by Pixabay on Pexels.

Knut is sitting at his desk, staring at a blank paper in front of him, and nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: “I need a plan!”

Knut is confronted with something every one of us encounters in his daily life: he has a problem, and he does not know how to solve it. But what exactly is a problem? Are there strategies to solve problems? These are just a few of the questions we want to answer in this chapter.

We begin our chapter by giving a short description of what psychologists regard as a problem. Afterward we will discuss different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts solve problems.

The most basic definition of a problem is any given situation that differs from a desired goal. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows us to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, learning, repeating and varying all kinds of complex movements, and so on. Though all of these problems were of crucial importance during the human evolutionary process, they are by no means solved exclusively by humans. We find an amazing variety of different solutions for these problems in nature (just consider, for example, the way a bat hunts its prey compared to a spider). We will mainly focus on problems that are not solved by animals or evolution; we will instead focus on abstract problems, such as playing chess. Furthermore, we will not consider problems that have an obvious solution. For example, imagine Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognizing the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. We will often find that the strategies we use to solve these problems are applicable to more basic problems, too.

Non-trivial, abstract problems can be divided into two groups: well-defined problems and ill- defined problems.

WELL-DEFINED PROBLEMS

For many abstract problems, it is possible to find an algorithmic solution. We call problems well-defined if they can be properly formalized, which involves the following properties:

•        The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later).

•        There is a finite set of operators, that is, rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.

•        Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.

A problem that fulfils these requirements can be implemented algorithmically. Therefore many well-defined problems can be very effectively solved by computers, like playing chess.

ILL-DEFINED PROBLEMS

Though many problems can be properly formalized, there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity, and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state. Formalizing a problem such as “Please paint a beautiful picture” may be impossible.

Still, this is a problem most people would be able to approach in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.

The line between well-defined and ill-defined problems is not always neat: ill-defined problems often involve sub-problems that can be perfectly well-defined. On the other hand, many everyday problems that seem to be completely well-defined involve — when examined in detail — a great amount of creativity and ambiguity. Consider Knut’s fairly ill-defined task of writing an essay: he will not be able to complete this task without first understanding the text he has to write about. This step is the first subgoal Knut has to solve. In this example, an ill-defined problem involves a well-defined sub-problem

RESTRUCTURING: THE GESTALTIST APPROACH

One dominant approach to problem solving originated from Gestalt psychologists in the 1920s. Their understanding of problem solving emphasizes behavior in situations requiring relatively novel means of attaining goals and suggests that problem solving involves a process called restructuring. With a Gestalt approach, two main questions have to be considered to understand the process of problem solving: 1) How is a problem represented in a person’s mind?, and 2) How does solving this problem involve a reorganization or restructuring of this representation?

HOW IS A PROBLEM REPRESENTED IN THE MIND?

In current research internal and external representations are distinguished: an internal representation is one held in memory, and which has to be retrieved by cognitive processes, while an external representation exists in the environment, such like physical objects or symbols whose information can be picked up and processed by the perceptual system.

Generally speaking, problem representations are models of the situation as experienced by the solver. Representing a problem means to analyze it and split it into separate components, including objects, predicates, state space, operators, and selection criteria.

The efficiency of problem solving depends on the underlying representations in a person’s mind, which usually also involves personal aspects. Re-analyzing the problem along different dimensions, or changing from one representation to another, can result in arriving at a new understanding of a problem. This is called restructuring . The following example illustrates this:

Two boys of different ages are playing badminton. The older one is a more skilled player, and therefore the outcome of matches between the two becomes predictable. After repeated defeats the younger boy finally loses interest in playing. The older boy now faces a problem, namely that he has no one to play with anymore. The usual options, according to M. Wertheimer (1945/82), range from “offering candy” and “playing a different game” to “not playing at full ability” and “shaming the younger boy into playing.” All of these strategies aim at making the younger boy stay.

The older boy instead comes up with a different solution: He proposes that they should try to keep the birdie in play as long as possible. Thus, they change from a game of competition to one of cooperation. The proposal is happily accepted, and the game is on again. The key in this story is that the older boy restructured the problem, having found that his attitude toward the game made it difficult to keep the younger boy playing. With the new type of game the problem is solved: the older boy is not bored, and the younger boy is not frustrated. In some cases, new representations can make a problem more difficult or much easier to solve. In the latter case insight – the sudden realization of a problem’s solution – may be the key to finding a solution.

There are two very different ways of approaching a goal-oriented situation . In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking .

The second way requires something new and di fferent to achieve the goal—prior learning is of little help here. Such productive thinking is sometimes argued to involve insight . Gestalt psychologists state that insight problems are a separate category of problems in their own right.

Tasks that might involve insight usually have certain features: they require something new and non-obvious to be done, and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called “aha” experience: the solution pops into mind all of a sudden. In one moment you have no idea how to answer the problem, and you feel you are not making any progress trying out different ideas, but in the next moment the problem is solved.

For readers who would like to experience such an effect, here is an example of an insight problem: Knut is given four pieces of a chain; each made up of three links. The task is to link it all up to a closed loop. To open a link costs 2 cents, and to close a link costs 3 cents. Knut has 15 cents to spend. What should Knut do?

If you want to know the correct solution, turn to the next page.

To show that solving insight problems involves restructuring , psychologists have created a number of problems that are more difficult to solve for participants with previous experiences, since it is harder for them to change the representation of the given situation.

For non-insight problems the opposite is the case. Solving arithmetical problems, for instance, requires schemas, through which one can get to the solution step by step.

Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation .

FUNCTIONAL FIXEDNESS

Functional fixedness concerns the solution of object use problems . The basic idea is that when the usual function an object is emphasized, it will be far more difficult for a person to use that object in a novel manner. An example for this effect is the candle problem : Imagine you are given a box of matches, some candles and tacks. On the wall of the room there is a cork-board. Your task is to fix the candle to the cork-board in such a way that no wax will drop on the floor when the candle is lit. Got an idea?

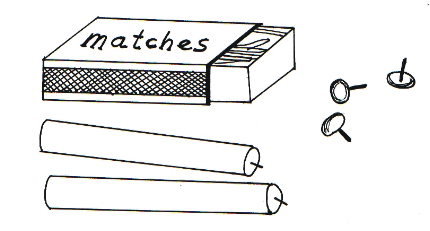
Here’s a clue: when people are confronted with a problem and given certain objects to solve it, it is difficult for them to figure out that they could use the objects in a different way. In this example, the box has to be recognized as a support rather than as a container— tack the matchbox to the wall, and place the candle upright in the box. The box will catch the falling wax.

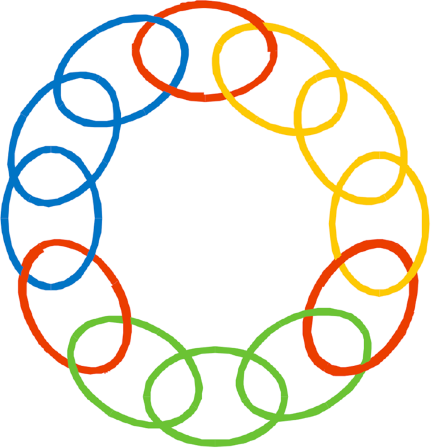
A further example is the two-string problem : Knut is left in a room with a pair of pliers and given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?

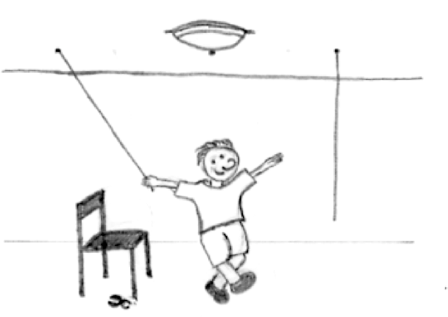
Solution: Knut has to recognize he can use the pliers in a novel function: as weight for a pendulum. He can tie them to one of the strings, push it away, hold the other string and wait for the first one to swing toward him.

MENTAL FIXEDNESS

Functional fixedness as involved in the examples above illustrates a mental set: a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulty varying the way of use (i.e., pliers as pendulum’s weight).

One approach to studying fixation was to study wrong-answer verbal insight problems . In these probems, people tend to give an incorrect answer when failing to solve a problem rather than to give no answer at all.

A typical example: People are told that on a lake the area covered by water lilies doubles every 24 hours and that it takes 60 days to cover the whole lake. Then they are asked how many days it takes to cover half the lake. The typical response is “30 days” (whereas 59 days is correct).

These wrong solutions are due to an inaccurate interpretation , or representation , of the problem. This can happen because of sloppiness (a quick shallow reading of the problem and/or weak monitoring of their efforts made to come to a solution). In this case error feedback should help people to reconsider the problem features, note the inadequacy of their first answer, and find the correct solution. If, however, people are truly fixated on their incorrect representation, being told the answer is wrong does not help. In a study by P.I. Dallop and

R.L. Dominowski in 1992 these two possibilities were investigated. In approximately one third of the cases error feedback led to right answers, so only approximately one third of the wrong answers were due to inadequate monitoring.

Another approach is the study of examples with and without a preceding analogous task. In cases such like the water-jug task, analogous thinking indeed leads to a correct solution, but to take a different way might make the case much simpler:

Imagine Knut again, this time he is given three jugs with different capacities and is asked to measure the required amount of water. He is not allowed to use anything except the jugs and as much water as he likes. In the first case the sizes are: 127 cups, 21 cups and 3 cups. His goal is to measure 100 cups of water.

In the second case Knut is asked to measure 18 cups from jugs of 39, 15 and 3 cups capacity.

Participants who are given the 100 cup task first choose a complicated way to solve the second task. Participants who did not know about that complex task solved the 18 cup case by just adding three cups to 15.

SOLVING PROBLEMS BY ANALOGY

One special kind of restructuring is analogical problem solving. Here, to find a solution to one problem (i.e., the target problem) an analogous solution to another problem (i.e., the base problem) is presented.

An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:

As a doctor you have to treat a patient with a malignant, inoperable tumor, buried deep inside the body. There exists a special kind of ray which is harmless at a low intensity, but at sufficiently high intensity is able to destroy the tumor. At such high intensity, however, the ray will also destroy the healthy tissue it passes through on the way to the tumor. What can be done to destroy the tumor while preserving the healthy tissue?

When this question was asked to participants in an experiment, most of them couldn’t come up with the appropriate answer to the problem. Then they were told a story that went something like this:

A general wanted to capture his enemy’s fortress. He gathered a large army to launch a full- scale direct attack, but then learned that all the roads leading directly towards the fortress were blocked by landmines. These roadblocks were designed in such a way that it was possible for small groups of the fortress-owner’s men to pass over them safely, but a large group of men would set them off. The general devised the following plan: He divided his troops into several smaller groups and ordered each of them to march down a different road, timed in such a way that the entire army would reunite exactly when reaching the fortress and could hit with full strength.

Here, the story about the general is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumor and the big army corresponds to the highly intensive ray. Likewise, a small group of soldiers represents a ray at low intensity. The s olution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumor from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumor itself gets destroyed by the ray at its full intensity.

M. Gick and K. Holyoak presented Duncker’s radiation problem to a group of participants in 1980 and 1983. 10 percent of participants were able to solve the problem right away, but 30 percent could solve it when they read the story of the general before. After being given an additional hint — to use the story as help — 75 percent of them solved the problem.

Following these results, Gick and Holyoak concluded that analogical problem solving consists of three steps:

1.  Recognizing that an analogical connection exists between the source and the base problem.

2. Mapping corresponding parts of the two problems onto each other (fortress ® tumour, army ® ray, etc.)

3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions ® sending several weaker rays from different directions)

Next, Gick and Holyoak started looking for factors that could help the recognizing and mapping processes.

The abstract concept that links the target problem with the base problem is called the problem schema. Gick and Holyoak facilitated the activation of a schema with their participants by giving them two stories and asking them to compare and summarize them. This activation of problem schemas is called “schema induction“.

The experimenters had participants read stories that presented problems and their solutions. One story was the above story about the general, and other stories required the same problem schema (i.e., if a heavy force coming from one direction is not suitable, use multiple smaller forces that simultaneously converge on the target). The experimenters manipulated how many of these stories the participants read before the participants were asked to solve the radiation problem. The experiment showed that in order to solve the target problem, reading two stories with analogical problems is more helpful than reading only one story. This evidence suggests that schema induction can be achieved by exposing people to multiple problems with the same problem schema.

HOW DO EXPERTS SOLVE PROBLEMS?

An expert is someone who devotes large amounts of their time and energy to one specific field of interest in which they, subsequently, reach a certain level of mastery. It should not be a surprise that experts tend to be better at solving problems in their field than novices (i.e., people who are beginners or not as well-trained in a field as experts) are. Experts are faster at coming up with solutions and have a higher rate of correct solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:

1.       Experts know more about their field,

2.      their knowledge is organized differently, and

3.      they spend more time analyzing the problem.

Expertise is domain specific— when it comes to problems that are outside the experts’ domain of expertise, their performance often does not differ from that of novices.

Knowledge: An experiment by Chase and Simon (1973) dealt with the question of how well experts and novices are able to reproduce positions of chess pieces on chess boards after a brief presentation. The results showed that experts were far better at reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognize familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not only the amount of knowledge that makes an expert more successful. Experts also organize their knowledge differently from novices.

Organization: In 1981 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. The students tended to group the problems based on their surface structure (i.e., similarities of objects used in the problem, such as sketches illustrating the problem), whereas the professors used their deep structure (i.e., the general physical principles that underlie the problems) as criteria. By recognizing the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g., another problem they solved earlier which required the same strategy).

Analysis: Experts often spend more time analyzing a problem before actually trying to solve it. This way of approaching a problem may often result in what appears to be a slow start, but in the long run this strategy is much more effective. A novice, on the other hand, might start working on the problem right away, but often reach dead ends as they chose a wrong path in the very beginning.

_________________________________________________________________________________________________________________________________________________________

Chase, W. G., & Simon, H. A. (1973). Perception in chess. Cognitive psychology, 4(1), 55-81.

Chi, M. T., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive science, 5(2), 121-152.

Duncker, K., & Lees, L. S. (1945). On problem-solving. Psychological monographs, 58(5).

Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive psychology, 12(3), 306-355. Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive psychology, 15(1), 1-38.

Goldstein, E.B. (2005). Cogntive Psychology. Connecting Mind, Research, and Everyday Experience. Belmont: Thomson Wadsworth.

R.L. Dominowski and P. Dallob, Insight and Problem Solving. In The Nature of Insight, R.J. Sternberg & J.E. Davidson (Eds). MIT Press: USA, pp.33-62 (1995).

Wertheimer, M., (1945). Productive thinking. New York: Harper.

ESSENTIALS OF COGNITIVE PSYCHOLOGY Copyright © 2023 by Christopher Klein is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Explore Psychology

Psychology Articles, Study Guides, and Resources

Insight Learning Theory: Definition, Stages, and Examples

Insight learning theory is all about those “lightbulb moments” we experience when we suddenly understand something. Instead of slowly figuring things out through trial and error, insight theory says we can suddenly see the solution to a problem in our minds.  This theory is super important because it helps us understand how our brains work…

Insight learning theory is all about those “lightbulb moments” we experience when we suddenly understand something. Instead of slowly figuring things out through trial and error, insight theory says we can suddenly see the solution to a problem in our minds. 

This theory is super important because it helps us understand how our brains work when we learn and solve problems. It can help teachers find better ways to teach and improve our problem-solving skills and creativity. It’s not just useful in school—insight theory also greatly impacts science, technology, and business.

In this article

What Is Insight Learning?

Insight learning is like having a lightbulb moment in your brain. It’s when you suddenly understand something without needing to go through a step-by-step process. Instead of slowly figuring things out by trial and error, insight learning happens in a flash. One moment, you’re stuck, and the next, you have the solution. 

This type of learning is all about those “aha” experiences that feel like magic. The key principles of insight learning involve recognizing patterns, making connections, and restructuring our thoughts. It’s as if our brains suddenly rearrange the pieces of a puzzle, revealing the big picture. So, next time you have a brilliant idea pop into your head out of nowhere, you might just be experiencing insight learning in action!

Three Components of Insight Learning Theory

Insight learning, a concept rooted in psychology, comprises three distinct properties that characterize its unique nature:

1. Sudden Realization

Unlike gradual problem-solving methods, insight learning involves sudden and profound understanding. Individuals may be stuck on a problem for a while, but then, seemingly out of nowhere, the solution becomes clear. This sudden “aha” moment marks the culmination of mental processes that have been working behind the scenes to reorganize information and generate a new perspective .

2. Restructuring of Problem-Solving Strategies

Insight learning often involves a restructuring of mental representations or problem-solving strategies . Instead of simply trying different approaches until stumbling upon the correct one, individuals experience a shift in how they perceive and approach the problem. This restructuring allows for a more efficient and direct path to the solution once insight occurs.

3. Aha Moments

A hallmark of insight learning is the experience of “aha” moments. These moments are characterized by a sudden sense of clarity and understanding, often accompanied by a feeling of satisfaction or excitement. It’s as if a mental lightbulb turns on, illuminating the solution to a previously perplexing problem. 

These moments of insight can be deeply rewarding and serve as powerful motivators for further learning and problem-solving endeavors.

Four Stages of Insight Learning Theory

Insight learning unfolds in a series of distinct stages, each contributing to the journey from problem recognition to the sudden realization of a solution. These stages are as follows:

1. Problem Recognition

The first stage of insight learning involves recognizing and defining the problem at hand. This may entail identifying obstacles, discrepancies, or gaps in understanding that need to be addressed. Problem recognition sets the stage for the subsequent stages of insight learning by framing the problem and guiding the individual’s cognitive processes toward finding a solution.

2. Incubation

After recognizing the problem, individuals often enter a period of incubation where the mind continues to work on the problem unconsciously. During this stage, the brain engages in background processing, making connections, and reorganizing information without the individual’s conscious awareness. 

While it may seem like a period of inactivity on the surface, incubation is a crucial phase where ideas gestate, and creative solutions take shape beneath the surface of conscious thought.

3. Illumination

The illumination stage marks the sudden emergence of insight or understanding. It is characterized by a moment of clarity and realization, where the solution to the problem becomes apparent in a flash of insight. 

This “aha” moment often feels spontaneous and surprising, as if the solution has been waiting just below the surface of conscious awareness to be revealed. Illumination is the culmination of the cognitive processes initiated during problem recognition and incubation, resulting in a breakthrough in understanding.

4. Verification

Following the illumination stage, individuals verify the validity and feasibility of their insights by testing the proposed solution. This may involve applying the solution in practice, checking it against existing knowledge or expertise, or seeking feedback from others. 

Verification serves to confirm the efficacy of the newfound understanding and ensure its practical applicability in solving the problem at hand. It also provides an opportunity to refine and iterate on the solution based on real-world feedback and experience.

Famous Examples of Insight Learning

Examples of insight learning can be observed in various contexts, ranging from everyday problem-solving to scientific discoveries and creative breakthroughs. Some well-known examples of how insight learning theory works include the following:

Archimedes’ Principle

According to legend, the ancient Greek mathematician Archimedes experienced a moment of insight while taking a bath. He noticed that the water level rose as he immersed his body, leading him to realize that the volume of water displaced was equal to the volume of the submerged object. This insight led to the formulation of Archimedes’ principle, a fundamental concept in fluid mechanics.

Köhler’s Chimpanzee Experiments

In Wolfgang Köhler’s experiments with chimpanzees on Tenerife in the 1920s, the primates demonstrated insight learning in solving novel problems. One famous example involved a chimpanzee named Sultan, who used sticks to reach bananas placed outside his cage. After unsuccessful attempts at using a single stick, Sultan suddenly combined two sticks to create a longer tool, demonstrating insight into the problem and the ability to use tools creatively.

Eureka Moments in Science

Many scientific discoveries are the result of insight learning. For instance, the famed naturalist Charles Darwin had many eureka moments where he gained sudden insights that led to the formation of his influential theories.

Everyday Examples of Insight Learning Theory

You can probably think of some good examples of the role that insight learning theory plays in your everyday life. A few common real-life examples include:

• Finding a lost item : You might spend a lot of time searching for a lost item, like your keys or phone, but suddenly remember exactly where you left them when you’re doing something completely unrelated. This sudden recollection is an example of insight learning.
• Untangling knots : When trying to untangle a particularly tricky knot, you might struggle with it for a while without making progress. Then, suddenly, you realize a new approach or see a pattern that helps you quickly unravel the knot.
• Cooking improvisation : If you’re cooking and run out of a particular ingredient, you might suddenly come up with a creative substitution or alteration to the recipe that works surprisingly well. This moment of improvisation demonstrates insight learning in action.
• Solving riddles or brain teasers : You might initially be stumped when trying to solve a riddle or a brain teaser. However, after some time pondering the problem, you suddenly grasp the solution in a moment of insight.
• Learning a new skill : Learning to ride a bike or play a musical instrument often involves moments of insight. You might struggle with a certain technique or concept but then suddenly “get it” and experience a significant improvement in your performance.
• Navigating a maze : While navigating through a maze, you might encounter dead ends and wrong turns. However, after some exploration, you suddenly realize the correct path to take and reach the exit efficiently.
• Remembering information : When studying for a test, you might find yourself unable to recall a particular piece of information. Then, when you least expect it, the answer suddenly comes to you in a moment of insight.

These everyday examples illustrate how insight learning is a common and natural part of problem-solving and learning in our daily lives.

Exploring the Uses of Insight Learning

Insight learning isn’t an interesting explanation for how we suddenly come up with a solution to a problem—it also has many practical applications. Here are just a few ways that people can use insight learning in real life:

Problem-Solving

Insight learning helps us solve all sorts of problems, from finding lost items to untangling knots. When we’re stuck, our brains might suddenly come up with a genius idea or a new approach that saves the day. It’s like having a mental superhero swoop in to rescue us when we least expect it!

Ever had a brilliant idea pop into your head out of nowhere? That’s insight learning at work! Whether you’re writing a story, composing music, or designing something new, insight can spark creativity and help you come up with fresh, innovative ideas.

Learning New Skills

Learning isn’t always about memorizing facts or following step-by-step instructions. Sometimes, it’s about having those “aha” moments that make everything click into place. Insight learning can help us grasp tricky concepts, master difficult skills, and become better learners overall.

Insight learning isn’t just for individuals—it’s also crucial for innovation and progress in society. Scientists, inventors, and entrepreneurs rely on insight to make groundbreaking discoveries and develop new technologies that improve our lives. Who knows? The next big invention could start with someone having a brilliant idea in the shower!

Overcoming Challenges

Life is full of challenges, but insight learning can help us tackle them with confidence. Whether it’s navigating a maze, solving a puzzle, or facing a tough decision, insight can provide the clarity and creativity we need to overcome obstacles and achieve our goals.

The next time you’re feeling stuck or uninspired, remember: the solution might be just one “aha” moment away!

Alternatives to Insight Learning Theory

While insight learning theory emphasizes sudden understanding and restructuring of problem-solving strategies, several alternative theories offer different perspectives on how learning and problem-solving occur. Here are some of the key alternative theories:

Behaviorism

Behaviorism is a theory that focuses on observable, overt behaviors and the external factors that influence them. According to behaviorists like B.F. Skinner, learning is a result of conditioning, where behaviors are reinforced or punished based on their consequences. 

In contrast to insight learning theory, behaviorism suggests that learning occurs gradually through repeated associations between stimuli and responses rather than sudden insights or realizations.

Cognitive Learning Theory

Cognitive learning theory, influenced by psychologists such as Jean Piaget and Lev Vygotsky , emphasizes the role of mental processes in learning. This theory suggests that individuals actively construct knowledge and understanding through processes like perception, memory, and problem-solving. 

Cognitive learning theory acknowledges the importance of insight and problem-solving strategies but places greater emphasis on cognitive structures and processes underlying learning.

Gestalt Psychology

Gestalt psychology, which influenced insight learning theory, proposes that learning and problem-solving involve the organization of perceptions into meaningful wholes or “gestalts.” 

Gestalt psychologists like Max Wertheimer emphasized the role of insight and restructuring in problem-solving, but their theories also consider other factors, such as perceptual organization, pattern recognition, and the influence of context.

Information Processing Theory

Information processing theory views the mind as a computer-like system that processes information through various stages, including input, processing, storage, and output. This theory emphasizes the role of attention, memory, and problem-solving strategies in learning and problem-solving. 

While insight learning theory focuses on sudden insights and restructuring, information processing theory considers how individuals encode, manipulate, and retrieve information to solve problems.

Related reading:

• What Is Kolb’s Learning Cycle?
• What Is Latent Learning?

What Is Scaffolding in Psychology?

• What Is Observational Learning?

Kizilirmak, J. M., Fischer, L., Krause, J., Soch, J., Richter, A., & Schott, B. H. (2021). Learning by insight-like sudden comprehension as a potential strategy to improve memory encoding in older adults .  Frontiers in Aging Neuroscience ,  13 , 661346. https://doi.org/10.3389/fnagi.2021.661346

Lind, J., Enquist, M. (2012). Insight learning and shaping . In: Seel, N.M. (eds) Encyclopedia of the Sciences of Learning . Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1428-6_851

Osuna-Mascaró, A. J., & Auersperg, A. M. I. (2021). Current understanding of the “insight” phenomenon across disciplines . Frontiers in Psychology , 12, 791398. https://doi.org/10.3389/fpsyg.2021.791398

Salmon-Mordekovich, N., & Leikin, M. (2023). Insight problem solving is not that special, but business is not quite ‘as usual’: typical versus exceptional problem-solving strategies .  Psychological Research ,  87 (6), 1995–2009. https://doi.org/10.1007/s00426-022-01786-5

Explore Psychology covers psychology topics to help people better understand the human mind and behavior. Our team covers studies and trends in the modern world of psychology and well-being.

Related Articles:

What is Kolb’s Learning Cycle and How Does it Work?

David A. Kolb, an influential American educational theorist, is best known for his work on experiential learning theory. Central to this theory is Kolb’s learning cycle, which comprises four stages: Concrete Experience, Reflective Observation, Abstract Conceptualization, and Active Experimentation. This cycle explains how individuals learn through a continuous process of experiencing, reflecting, conceptualizing, and experimenting. …

Kinesthetic Learning: Definition and Examples

Hands-on learning that helps you master new skills.

What Is Observational Learning in Psychology?

There are many ways to learn, but one of the most common involves observing what other people are doing. Consider how often you watch others, whether it’s a family member, a teacher, or your favorite YouTuber. This article explores the theory of observational learning, the steps that are involved, and some of the factors that…

What Is Latent Learning? Definition and Examples

Latent learning refers to learning that is not immediately displayed. Essentially, it learning that happens as you live your life. You might not consciously try to notice and remember it, but your brain picks it up anyway. While you might not demonstrate such learning right away, it’s something that might come in handy later when…

What Are Kolb’s Learning Styles?

Learn about the diverging, assimilating, converging, and accommodating styles.

Scaffolding refers to the temporary support that adults or other competent peers offer when a person is learning a new skill or trying to accomplish a task.  The concept was first introduced by the Russian psychologist Lev Vygotsky, who was best known for his theories that emphasized the importance of social interaction in the learning…

Thinking and Intelligence

Introduction to Thinking and Problem-Solving

What you’ll learn to do: describe cognition and problem-solving strategies.

Imagine all of your thoughts as if they were physical entities, swirling rapidly inside your mind. How is it possible that the brain is able to move from one thought to the next in an organized, orderly fashion? The brain is endlessly perceiving, processing, planning, organizing, and remembering—it is always active. Yet, you don’t notice most of your brain’s activity as you move throughout your daily routine. This is only one facet of the complex processes involved in cognition. Simply put, cognition is thinking, and it encompasses the processes associated with perception, knowledge, problem solving, judgment, language, and memory. Scientists who study cognition are searching for ways to understand how we integrate, organize, and utilize our conscious cognitive experiences without being aware of all of the unconscious work that our brains are doing (for example, Kahneman, 2011).

Learning Objectives

• Distinguish between concepts and prototypes
• Explain the difference between natural and artificial concepts
• Describe problem solving strategies, including algorithms and heuristics
• Explain some common roadblocks to effective problem solving

CC licensed content, Original

• Modification, adaptation, and original content. Provided by : Lumen Learning. License : CC BY: Attribution

CC licensed content, Shared previously

• What Is Cognition?. Authored by : OpenStax College. Located at : https://openstax.org/books/psychology-2e/pages/7-1-what-is-cognition . License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction
• A Thinking Man Image. Authored by : Wesley Nitsckie. Located at : https://www.flickr.com/photos/nitsckie/5507777269 . License : CC BY-SA: Attribution-ShareAlike

General Psychology Copyright © by OpenStax and Lumen Learning is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• Skip to main content
• Skip to primary sidebar

IResearchNet

Problem Solving

Problem solving, a fundamental cognitive process deeply rooted in psychology, plays a pivotal role in various aspects of human existence, especially within educational contexts. This article delves into the nature of problem solving, exploring its theoretical underpinnings, the cognitive and psychological processes that underlie it, and the application of problem-solving skills within educational settings and the broader real world. With a focus on both theory and practice, this article underscores the significance of cultivating problem-solving abilities as a cornerstone of cognitive development and innovation, shedding light on its applications in fields ranging from education to clinical psychology and beyond, thereby paving the way for future research and intervention in this critical domain of human cognition.

Introduction

Problem solving, a quintessential cognitive process deeply embedded in the domains of psychology and education, serves as a linchpin for human intellectual development and adaptation to the ever-evolving challenges of the world. The fundamental capacity to identify, analyze, and surmount obstacles is intrinsic to human nature and has been a subject of profound interest for psychologists, educators, and researchers alike. This article aims to provide a comprehensive exploration of problem solving, investigating its theoretical foundations, cognitive intricacies, and practical applications in educational contexts. With a clear understanding of its multifaceted nature, we will elucidate the pivotal role that problem solving plays in enhancing learning, fostering creativity, and promoting cognitive growth, setting the stage for a detailed examination of its significance in both psychology and education. In the continuum of psychological research and educational practice, problem solving stands as a cornerstone, enabling individuals to navigate the complexities of their world. This article’s thesis asserts that problem solving is not merely a cognitive skill but a dynamic process with profound implications for intellectual growth and application in diverse real-world contexts.

The Nature of Problem Solving

Problem solving, within the realm of psychology, refers to the cognitive process through which individuals identify, analyze, and resolve challenges or obstacles to achieve a desired goal. It encompasses a range of mental activities, such as perception, memory, reasoning, and decision-making, aimed at devising effective solutions in the face of uncertainty or complexity.

Problem solving as a subject of inquiry has drawn from various theoretical perspectives, each offering unique insights into its nature. Among the seminal theories, Gestalt psychology has highlighted the role of insight and restructuring in problem solving, emphasizing that individuals often reorganize their mental representations to attain solutions. Information processing theories, inspired by computer models, emphasize the systematic and step-by-step nature of problem solving, likening it to information retrieval and manipulation. Furthermore, cognitive psychology has provided a comprehensive framework for understanding problem solving by examining the underlying cognitive processes involved, such as attention, memory, and decision-making. These theoretical foundations collectively offer a richer comprehension of how humans engage in and approach problem-solving tasks.

Problem solving is not a monolithic process but a series of interrelated stages that individuals progress through. These stages are integral to the overall problem-solving process, and they include:

• Problem Representation: At the outset, individuals must clearly define and represent the problem they face. This involves grasping the nature of the problem, identifying its constraints, and understanding the relationships between various elements.
• Goal Setting: Setting a clear and attainable goal is essential for effective problem solving. This step involves specifying the desired outcome or solution and establishing criteria for success.
• Solution Generation: In this stage, individuals generate potential solutions to the problem. This often involves brainstorming, creative thinking, and the exploration of different strategies to overcome the obstacles presented by the problem.
• Solution Evaluation: After generating potential solutions, individuals must evaluate these alternatives to determine their feasibility and effectiveness. This involves comparing solutions, considering potential consequences, and making choices based on the criteria established in the goal-setting phase.

These components collectively form the roadmap for navigating the terrain of problem solving and provide a structured approach to addressing challenges effectively. Understanding these stages is crucial for both researchers studying problem solving and educators aiming to foster problem-solving skills in learners.

Cognitive and Psychological Aspects of Problem Solving

Problem solving is intricately tied to a range of cognitive processes, each contributing to the effectiveness of the problem-solving endeavor.

• Perception: Perception serves as the initial gateway in problem solving. It involves the gathering and interpretation of sensory information from the environment. Effective perception allows individuals to identify relevant cues and patterns within a problem, aiding in problem representation and understanding.
• Memory: Memory is crucial in problem solving as it enables the retrieval of relevant information from past experiences, learned strategies, and knowledge. Working memory, in particular, helps individuals maintain and manipulate information while navigating through the various stages of problem solving.
• Reasoning: Reasoning encompasses logical and critical thinking processes that guide the generation and evaluation of potential solutions. Deductive and inductive reasoning, as well as analogical reasoning, play vital roles in identifying relationships and formulating hypotheses.

While problem solving is a universal cognitive function, individuals differ in their problem-solving skills due to various factors.

• Intelligence: Intelligence, as measured by IQ or related assessments, significantly influences problem-solving abilities. Higher levels of intelligence are often associated with better problem-solving performance, as individuals with greater cognitive resources can process information more efficiently and effectively.
• Creativity: Creativity is a crucial factor in problem solving, especially in situations that require innovative solutions. Creative individuals tend to approach problems with fresh perspectives, making novel connections and generating unconventional solutions.
• Expertise: Expertise in a specific domain enhances problem-solving abilities within that domain. Experts possess a wealth of knowledge and experience, allowing them to recognize patterns and solutions more readily. However, expertise can sometimes lead to domain-specific biases or difficulties in adapting to new problem types.

Despite the cognitive processes and individual differences that contribute to effective problem solving, individuals often encounter barriers that impede their progress. Recognizing and overcoming these barriers is crucial for successful problem solving.

• Functional Fixedness: Functional fixedness is a cognitive bias that limits problem solving by causing individuals to perceive objects or concepts only in their traditional or “fixed” roles. Overcoming functional fixedness requires the ability to see alternative uses and functions for objects or ideas.
• Confirmation Bias: Confirmation bias is the tendency to seek, interpret, and remember information that confirms preexisting beliefs or hypotheses. This bias can hinder objective evaluation of potential solutions, as individuals may favor information that aligns with their initial perspectives.
• Mental Sets: Mental sets are cognitive frameworks or problem-solving strategies that individuals habitually use. While mental sets can be helpful in certain contexts, they can also limit creativity and flexibility when faced with new problems. Recognizing and breaking out of mental sets is essential for overcoming this barrier.

Understanding these cognitive processes, individual differences, and common obstacles provides valuable insights into the intricacies of problem solving and offers a foundation for improving problem-solving skills and strategies in both educational and practical settings.

Problem Solving in Educational Settings

Problem solving holds a central position in educational psychology, as it is a fundamental skill that empowers students to navigate the complexities of the learning process and prepares them for real-world challenges. It goes beyond rote memorization and standardized testing, allowing students to apply critical thinking, creativity, and analytical skills to authentic problems. Problem-solving tasks in educational settings range from solving mathematical equations to tackling complex issues in subjects like science, history, and literature. These tasks not only bolster subject-specific knowledge but also cultivate transferable skills that extend beyond the classroom.

Problem-solving skills offer numerous advantages to both educators and students. For teachers, integrating problem-solving tasks into the curriculum allows for more engaging and dynamic instruction, fostering a deeper understanding of the subject matter. Additionally, it provides educators with insights into students’ thought processes and areas where additional support may be needed. Students, on the other hand, benefit from the development of critical thinking, analytical reasoning, and creativity. These skills are transferable to various life situations, enhancing students’ abilities to solve complex real-world problems and adapt to a rapidly changing society.

Teaching problem-solving skills is a dynamic process that requires effective pedagogical approaches. In K-12 education, educators often use methods such as the problem-based learning (PBL) approach, where students work on open-ended, real-world problems, fostering self-directed learning and collaboration. Higher education institutions, on the other hand, employ strategies like case-based learning, simulations, and design thinking to promote problem solving within specialized disciplines. Additionally, educators use scaffolding techniques to provide support and guidance as students develop their problem-solving abilities. In both K-12 and higher education, a key component is metacognition, which helps students become aware of their thought processes and adapt their problem-solving strategies as needed.

Assessing problem-solving abilities in educational settings involves a combination of formative and summative assessments. Formative assessments, including classroom discussions, peer evaluations, and self-assessments, provide ongoing feedback and opportunities for improvement. Summative assessments may include standardized tests designed to evaluate problem-solving skills within a particular subject area. Performance-based assessments, such as essays, projects, and presentations, offer a holistic view of students’ problem-solving capabilities. Rubrics and scoring guides are often used to ensure consistency in assessment, allowing educators to measure not only the correctness of answers but also the quality of the problem-solving process. The evolving field of educational technology has also introduced computer-based simulations and adaptive learning platforms, enabling precise measurement and tailored feedback on students’ problem-solving performance.

Understanding the pivotal role of problem solving in educational psychology, the diverse pedagogical strategies for teaching it, and the methods for assessing and measuring problem-solving abilities equips educators and students with the tools necessary to thrive in educational environments and beyond. Problem solving remains a cornerstone of 21st-century education, preparing students to meet the complex challenges of a rapidly changing world.

Applications and Practical Implications

Problem solving is not confined to the classroom; it extends its influence to various real-world contexts, showcasing its relevance and impact. In business, problem solving is the driving force behind product development, process improvement, and conflict resolution. For instance, companies often use problem-solving methodologies like Six Sigma to identify and rectify issues in manufacturing. In healthcare, medical professionals employ problem-solving skills to diagnose complex illnesses and devise treatment plans. Additionally, technology advancements frequently stem from creative problem solving, as engineers and developers tackle challenges in software, hardware, and systems design. Real-world problem solving transcends specific domains, as individuals in diverse fields address multifaceted issues by drawing upon their cognitive abilities and creative problem-solving strategies.

Clinical psychology recognizes the profound therapeutic potential of problem-solving techniques. Problem-solving therapy (PST) is an evidence-based approach that focuses on helping individuals develop effective strategies for coping with emotional and interpersonal challenges. PST equips individuals with the skills to define problems, set realistic goals, generate solutions, and evaluate their effectiveness. This approach has shown efficacy in treating conditions like depression, anxiety, and stress, emphasizing the role of problem-solving abilities in enhancing emotional well-being. Furthermore, cognitive-behavioral therapy (CBT) incorporates problem-solving elements to help individuals challenge and modify dysfunctional thought patterns, reinforcing the importance of cognitive processes in addressing psychological distress.

Problem solving is the bedrock of innovation and creativity in various fields. Innovators and creative thinkers use problem-solving skills to identify unmet needs, devise novel solutions, and overcome obstacles. Design thinking, a problem-solving approach, is instrumental in product design, architecture, and user experience design, fostering innovative solutions grounded in human needs. Moreover, creative industries like art, literature, and music rely on problem-solving abilities to transcend conventional boundaries and produce groundbreaking works. By exploring alternative perspectives, making connections, and persistently seeking solutions, creative individuals harness problem-solving processes to ignite innovation and drive progress in all facets of human endeavor.

Understanding the practical applications of problem solving in business, healthcare, technology, and its therapeutic significance in clinical psychology, as well as its indispensable role in nurturing innovation and creativity, underscores its universal value. Problem solving is not only a cognitive skill but also a dynamic force that shapes and improves the world we inhabit, enhancing the quality of life and promoting progress and discovery.

In summary, problem solving stands as an indispensable cornerstone within the domains of psychology and education. This article has explored the multifaceted nature of problem solving, from its theoretical foundations rooted in Gestalt psychology, information processing theories, and cognitive psychology to its integral components of problem representation, goal setting, solution generation, and solution evaluation. It has delved into the cognitive processes underpinning effective problem solving, including perception, memory, and reasoning, as well as the impact of individual differences such as intelligence, creativity, and expertise. Common barriers to problem solving, including functional fixedness, confirmation bias, and mental sets, have been examined in-depth.

The significance of problem solving in educational settings was elucidated, underscoring its pivotal role in fostering critical thinking, creativity, and adaptability. Pedagogical approaches and assessment methods were discussed, providing educators with insights into effective strategies for teaching and evaluating problem-solving skills in K-12 and higher education.

Furthermore, the practical implications of problem solving were demonstrated in the real world, where it serves as the driving force behind advancements in business, healthcare, and technology. In clinical psychology, problem-solving therapies offer effective interventions for emotional and psychological well-being. The symbiotic relationship between problem solving and innovation and creativity was explored, highlighting the role of this cognitive process in pushing the boundaries of human accomplishment.

As we conclude, it is evident that problem solving is not merely a skill but a dynamic process with profound implications. It enables individuals to navigate the complexities of their environment, fostering intellectual growth, adaptability, and innovation. Future research in the field of problem solving should continue to explore the intricate cognitive processes involved, individual differences that influence problem-solving abilities, and innovative teaching methods in educational settings. In practice, educators and clinicians should continue to incorporate problem-solving strategies to empower individuals with the tools necessary for success in education, personal development, and the ever-evolving challenges of the real world. Problem solving remains a steadfast ally in the pursuit of knowledge, progress, and the enhancement of human potential.

References:

• Anderson, J. R. (1995). Cognitive psychology and its implications. W. H. Freeman.
• Atkinson, R. C., & Shiffrin, R. M. (1968). Human memory: A proposed system and its control processes. In The psychology of learning and motivation (Vol. 2, pp. 89-195). Academic Press.
• Duncker, K. (1945). On problem-solving. Psychological Monographs, 58(5), i-113.
• Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology, 12(3), 306-355.
• Jonassen, D. H., & Hung, W. (2008). All problems are not equal: Implications for problem-based learning. Interdisciplinary Journal of Problem-Based Learning, 2(2), 6.
• Kitchener, K. S., & King, P. M. (1981). Reflective judgment: Concepts of justification and their relation to age and education. Journal of Applied Developmental Psychology, 2(2), 89-116.
• Luchins, A. S. (1942). Mechanization in problem solving: The effect of Einstellung. Psychological Monographs, 54(6), i-95.
• Mayer, R. E. (1992). Thinking, problem solving, cognition. W. H. Freeman.
• Newell, A., & Simon, H. A. (1972). Human problem solving (Vol. 104). Prentice-Hall Englewood Cliffs, NJ.
• Osborn, A. F. (1953). Applied imagination: Principles and procedures of creative problem solving (3rd ed.). Charles Scribner’s Sons.
• Polya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton University Press.
• Sternberg, R. J. (2003). Wisdom, intelligence, and creativity synthesized. Cambridge University Press.

Insight Learning (Definition+ 4 Stages + Examples)

Have you ever been so focused on a problem that it took stepping away for you to figure it out? You can’t find the solution when you’re looking at all of the moving parts, but once you get distracted with something else - “A-ha!” you have it. 

When a problem cannot be solved by applying an obvious step-by-step solving sequence,   Insight learning occurs when the mind rearranges the elements of the problem and finds connections that were not obvious in the initial presentation of the problem. People experience this as a sudden A-ha moment.

Humans aren’t the only species that have these “A-ha” moments. Work with other species helped psychologists understand the definition and stages of Insight Learning. This video is going to break down those stages and how you can help to move these “a-ha” moments along. 

What Is Insight Learning? 

Insight learning is a process that leads to a sudden realization regarding a problem. Often, the learner has tried to understand the problem, but steps away before the change in perception occurs. Insight learning is often compared to trial-and-error learning, but it’s slightly different.

Rather than just trying different random solutions, insight learning requires more comprehension. Learners aim to understand the relationships between the pieces of the puzzle. They use patterns, organization, and past knowledge to solve the problem at hand. 

Is Insight Learning Only Observed In Humans? 

Humans aren’t the only species that learn with insight. Not all species use this process - just the ones that are closest to us intellectually. Insight learning was first discovered not by observing humans, but by observing chimps. 

In the early 1900s, Wolfgang Köhler observed chimpanzees as they solved problems. Köhler’s most famous subject was a chimp named Sultan. The psychologist gave Sultan two sticks of different sizes and placed a banana outside of Sultan’s cage. He watched as Sultan looked at the sticks and tried to reach for the banana with no success. Eventually, Sultan gave up and got distracted. But it was during this time that Köhler noticed Sultan having an “epiphany.” The chimp went back to the sticks, placed one inside of the other, and used this to bring the banana to him. 

Since Köhler’s original observations took place, psychologists looked deeper into the insight process and when you are more likely to experience that “a-ha” moment. There isn’t an exact science to insight learning, but certain theories suggest that some places are better for epiphanies than others. 

Four Stages of Insight Learning 

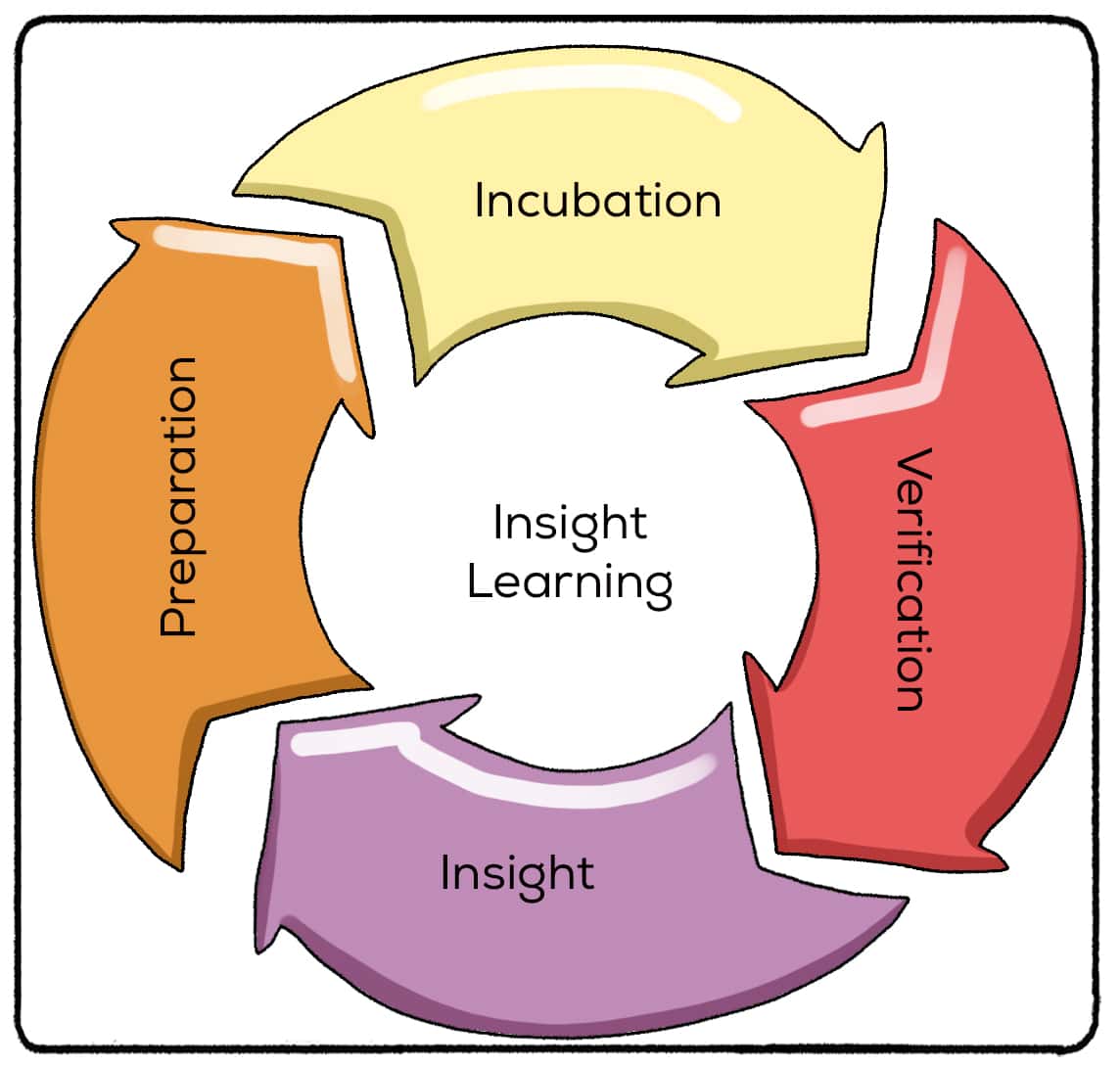
But how does insight learning happen? Multiple models have been developed, but the four-stage model is the most popular. The four stages of insight learning are preparation, incubation, insight, and verification. 

Preparation

The process begins as you try to solve the problem. You have the materials and information in front of you and begin to make connections. Although you see the relationships between the materials, things just haven’t “clicked” yet. This is the stage where you start to get frustrated. 

During the incubation period, you “give up” for a short period of time. Although you’ve abandoned the project, your brain is still making connections on an unconscious level. 

When the right connections have been made in your mind, the “a-ha” moment occurs. Eureka! You have an epiphany! 

Verification

Now, you just have to make sure that your epiphany is right. You test out your solution and hopefully, it works! This is a great moment in your learning journey. The connections you make solving this problem are likely to help you in the future. 

Examples of Insight Learning

Insight learning refers to the sudden realization or understanding of a solution to a problem without the need for trial-and-error attempts. It's like a "light bulb" moment when things suddenly make sense. Here are some examples of insight learning:

• The Matchstick Problem : Realizing you can light a match and use it to illuminate a dark room instead of fumbling around in the dark.
• Sudoku Puzzles : Suddenly seeing a pattern or number placement that you hadn't noticed before, allowing you to complete the puzzle.
• The Two Rope Problem : In an experiment, a person is given two ropes hanging from the ceiling and is asked to tie them together. The solution involves swinging one rope like a pendulum and grabbing it with the other.
• Opening Jars : After struggling to open a jar, you remember you can tap its lid lightly or use a rubber grip to make it easier.
• Tangram Puzzles : Suddenly realizing how to arrange the geometric pieces to complete the picture without any gaps.
• Escape Rooms : Having an "aha" moment about a clue that helps you solve a puzzle and move to the next challenge.
• The Nine Dot Problem : Connecting all nine dots using only four straight lines without lifting the pen.
• Cooking : Realizing you can soften butter quickly by grating it or placing it between two sheets of parchment paper and rolling it.
• Math Problems : Suddenly understanding a complex math concept or solution method after pondering it for a while.
• Guitar Tuning : Realizing you can use the fifth fret of one string to tune the next string.
• Traffic Routes : Discovering a faster or more efficient route to your destination without using a GPS.
• Packing Suitcases : Figuring out how to fit everything by rolling clothes or rearranging items in a specific order.
• The Crow and the Pitcher : A famous Aesop's fable where a thirsty crow drops pebbles into a pitcher to raise the water level and drink.
• Computer Shortcuts : Discovering a keyboard shortcut that makes a task you frequently do much quicker.
• Gardening : Realizing you can use eggshells or coffee grounds as a natural fertilizer.
• Physics Problems : After struggling with a concept, suddenly understanding the relationship between two variables in an equation.
• Art : Discovering a new technique or perspective that transforms your artwork.
• Sports : Realizing a different way to grip a tennis racket or baseball bat that improves your game.
• Language Learning : Suddenly understanding the grammar or pronunciation rule that was previously confusing.
• DIY Projects : Figuring out a way to repurpose old items in your home, like using an old ladder as a bookshelf.

Where Is the Best Place to Have an Epiphany? 

But what if you want to have an epiphany? You’re stuck on a problem and you can’t take it anymore. You want to abandon it, but you’re not sure what you should do for this epiphany to take place. Although an “a-ha” moment isn’t guaranteed, studies suggest that the following activities or places can help you solve a tough problem. 

The Three B’s of Creativity 

Creativity and divergent thinking are key to solving problems. And some places encourage creativity more than others. Researchers believe that you can kickstart divergent thinking with the three B’s: bed, bath, and the bus. 

Sleep 

“Bed” might be your best bet out of the three. Studies show that if you get a full night’s sleep, you will be twice as likely to solve a problem than if you stay up all night. This could be due to the REM sleep that you get throughout the night. During REM sleep , your brain is hard at work processing the day’s information and securing connections. Who knows - maybe you’ll dream up the answer to your problems tonight!

Meditation 

The word for “insight” in the Pali language is vipassana. If you have ever been interested in meditation , you might have seen this word before. You can do a vipassana meditation at home, or you can go to a 10-day retreat. These retreats are often silent and are set up to cultivate mind-body awareness. 

You certainly don’t have to sign up for a 10-day silent retreat to solve a problem that is bugging you. (Although, you may have a series of breakthroughs!) Try meditating for 20 minutes at a time. Studies show that this can increase the likelihood of solving a problem. 

Laugh! 

How do you feel when you have an epiphany? Good, right? The next time you’re trying to solve a problem, check in with your emotions. You are more likely to experience insight when you’re in a positive mood. Positivity opens your mind and gives your mind more freedom to explore. That exploration may just lead you to your solution. 

Be patient when you’re trying to solve problems. Take breaks when you need to and make sure that you are taking care of yourself. This approach will help you solve problems faster and more efficiently!

Insight Vs. Other Types Of Learning.

Learning by insight is  not  learning by trial and  error, nor by observation  and imitation. Learning by insight is a learning theory accepted by the Gestalt  school of psychology, which disagrees with the behaviorist  school, which claims that all learning occurs through conditioning from the  external environment.

Gestalt is a German word that approximately translates as ‘an organized whole  that has properties  and elements in addition to the sum of its parts .’ By viewing a problem as a ‘gestalt’ , the learner does not simply react to whatever she observes at the moment. She also imagines elements that could be present but are not and uses her imagination to combine parts of the problem that are presently not so combined in fact.  

Insight Vs. Trial And Error Learning

Imagine yourself in a maze-running competition. You and your rivals each have 10 goes. The first one to run the maze successfully wins $500. You may adopt a trial-and-error strategy, making random turning decisions and remembering whether those particular turns were successful or not for your next try. If you have a good memory and with a bit of luck, you will get to the exit and win the prize.

Completing the maze through trial and error requires no insight. If you had to run a different maze, you would have no advantage over running previous mazes with different designs. You have now learned to run this particular maze as predicted by behaviorist psychologists. External factors condition your maze running behavior. The cash prize motivates  you to run the maze in the first place. All maze dead ends act as punishments , which you remember not to repeat. All correct turns act as rewards , which you remember to repeat.

If you viewed the maze running competition as a gestalt, you might notice that it doesn't explicitly state in the competition rules that you must run along the designated paths to reach the exit.

Suppose you further noticed that the maze walls were made from cardboard. In that case, you may combine those 2 observations in your imagination and realize that you could just punch big holes in the walls or tear them down completely, to see around corners and directly run to the now visible exit.

Insight Vs. Learning Through Observation, Imitation, And Repetition

Observation, imitation, and repetition are at the heart of training. The violin teacher shows you how to hold your bow correctly; you practice your scales countless times before learning to play a sonata from Beethoven flawlessly. Mastering a sport or a musical instrument rarely comes from a flash of insight but a lot of repetition and error correction from your teacher.

Herbert Lawford, the Scottish tennis player, and 1887 Wimbledon champion, is credited for being the first player to play a topspin. Who could have taught it to him? Who could he have imitated? One can only speculate since no player at that time was being coached on how to hit topspin.

He could have only learned to play a topspin by having a novel insight. One possibility is that he played one by accident during training, by mistakenly hitting the ball at a flatter angle than normal. He could then have observed that his opponent was disorientated by the flatter and quicker bounce of the ball and realized the benefit of his ‘mistake’ .

Behaviorist theories of learning can probably explain how most successful and good tennis players are produced, but you need a Gestalt insight learning theory to explain Herbert Lawford.

Another interesting famous anecdote illustrating insight learning concerned Carl Friedrich Gauss when he was a 7-year-old pupil at school. His mathematics teacher seems to have adopted strict behaviorism in his teaching since the original story implies that he beat students with a switch.

One day the teacher set classwork requiring the students to add up all the numbers from 1 to 100. He expected his pupils to perform this calculation in how they were trained. He expected it to be a laborious and time-consuming task, giving him a long break. In just a few moments, young Gauss handed in the correct answer after having to make at most 2 calculations, which are easy to do in your head. How did he do it? Gauss saw the arithmetic sequence as a gestalt instead of adding all the numbers one at a time: 1+2+3+4…. +99+100 as he expected.

He realized that by breaking this sequence in half at 50, then snaking the last number (100) under the first number (1), and then adding the 2 halves of the arithmetic sequence like so:  

    1         +        2       +        3      +       4      +       5         +    ………….      +        48        +        49             +       50

100        +       99       +      98      +     97      +      96       +    …………...    +        53        +         52           +       51

101        +      101      +    101     +    101      +     101     +   …………….     +     101        +       101           +     101    

Arranged in this way, each number column adds up to 101, so all Gauss needed to do was calculate 50 x 101 = 5050.

Can Major Scientific Breakthroughs be made through observation and experiment alone?

Science is unapologetically an evidence-based inquiry. Observations, repeatable experiments, and hard, measurable data must support theories and explanations.

Since countless things can be observed and comparisons made, they cannot be done randomly for observations and experiments to advance knowledge. They must be guided by a good question and a  testable hypothesis. Before performing actual experiments and observations, scientists often first perform thought experiments . They think of ideal situations by imagining ways things could be or imaging away things that are.

Atoms were talked about long before electron microscopes could observe them. How could atoms be seriously discussed in ancient Greece long before the discoveries of modern chemistry? Pre-Socratic philosophers were puzzled by a purely philosophical problem, which they termed the problem of the one and many .  

People long observed that the world was made of many different things that didn't remain static but continuously changed into other various things. For example, a seed different from a tree changed into a tree over time. Small infants change into adults yet remain the same person. Boiling water became steam, and frozen water became ice.

Observing all of this in the world, philosophers didn’t simply take it for granted and aimed to profit from it practically through stimulus-response and trial and error learning. They were puzzled by how the world fit together as a whole.

To make sense of all this observable changing multiplicity, one needed to imagine an unobservable sameness behind it all. Yet, there is no obvious or immediate punishment or reward. Therefore, there seems to be no satisfying behaviorist reason behind philosophical speculations.

Thinkers such as Empedocles and Aristotle made associations between general properties in the world wetness, dryness, temperature, and phases of matter as follows:

• Earth :  dry, cold     
• Fire:  dry, hot
• Water:  wet, cold
• Air: hot or wet, depending on whether moisture or heat prevails in the atmosphere.

These 4 primitive elements transformed and combined give rise to the diversity we see in the world. However, this view was still too sensually based  to provide the world with sought-for coherence and unity. How could a multiplicity of truly basic stuff interact? Doesn't such an interaction presuppose something more fundamental in common?

The ratio of these 4 elements was thought to affect the properties of things. Stone contained more earth, while a rabbit had more water and fire, thus making it soft and giving it life. Although this theory correctly predicted that seemingly basic things like stones were complex compounds, it had some serious flaws.

For example, if you break a stone in half many times, the pieces never resemble fire, air, water, or earth.   

To account for how different things could be the same on one level and different on another level, Leucippus and his student Democritus reasoned that all things are the same in that they were made from some common primitive indivisible stuff but different due to the different ways or patterns in which this indivisible stuff or atoms could be arranged.

For atoms to be able to rearrange and recombine into different patterns led thinkers to the insight that if the atom idea was true, then logically, there had to be free spaces between the atoms for them to shift into. They had to imagine a vacuum, another phenomenon not directly observable since every nook and cranny in the world seems to be filled with some liquid, solid, or gas.  

This ancient notion of vacuum proved to be more than just a made-up story since it led to modern practical applications in the form of vacuum cleaners and food vacuum packing.

This insight that atoms and void exist makes no sense from a behaviorist learning standpoint. It cannot be explained in terms of stimulus-response or environmental conditioning and made no practical difference in the lives of ancient Greeks.  

For philosophers to feel compelled to hold onto notions, which at the time weren’t directly useful, it suggests that they must have felt some need to understand the universe as an intelligible ‘gestalt’ One may even argue that the word Cosmos, from the Greek word Kosmos, which roughly translates to ‘harmonious arrangement’ is at least a partial synonym.  

The Historical Development Of The Theory of Insight Learning

Wolfgang Kohler , the German gestalt psychologist, is credited for formulating the theory of insight learning, one of the first cognitive learning theories. He came up with the theory while first conducting experiments  in 1913 on 7 chimpanzees  on the island of Tenerife to observe how they learned to solve problems.

In one experiment, he dangled a banana from the top of a high cage. Boxes and poles were left in the cage with the chimpanzees. At first, the chimps used trial and error to get at the banana. They tried to jump up to the banana without success. After many failed attempts, Kohler noticed that they paused to think  for a while.  

After some time, they behaved more methodically by stacking the boxes on top of each other, making a raised platform from which they could swipe at the banana using the available poles. Kohler believed that chimps, like humans, were capable of experiencing flashes of insight, just like humans.

In another experiment, he placed a peanut down a long narrow tube attached to the cage's outer side. The chimpanzee tried scooping the peanut out with his hand and fingers, but to no avail, since the tube was too long and narrow. After sitting down to think, the chimp filled its mouth with water from a nearby water container in the cage and spat it into the tube.

The peanut floated up the tube within the chimp's reach. What is essential is that the chimp realized it could use water as a tool in a flash of insight, something it had never done before or never shown how  to do .  Kohler's conclusions contrasted with those of American psychologist Edward Thorndike , who, years back, conducted learning experiments on cats, dogs, and monkeys.

Through his experiments and research, Thorndike concluded that although there was a vast difference in learning speed and potential between monkey dogs and cats, he concluded that all animals, unlike humans, are not capable of genuine reasoned thought. According to him, Animals can only learn through stimulus-response conditioning, trial and error, and solve problems accidentally.

Kohler’s 4 Stage Model Of Insight Learning

From his observations of how chimpanzees solve complex problems, he concluded that the learning process went through the following 4 stages:

• Preparation:  Learners encounter the problem and begin to survey all relevant information and materials. They process stimuli and begin to make connections.
• Incubation: Learners get frustrated and may even seem to observers as giving up. However, their brains carry on processing information unconsciously.
• Insight: The learner finally achieves a breakthrough, otherwise called an epiphany or ‘Aha’ moment. This insight comes in a flash and is often a radical reorganization of the problem. It is a discontinuous leap in understanding rather than continuous with reasoning undertaken in the preparation phase.
• Verification: The learner now formally tests the new insight and sees if it works in multiple different situations. Mathematical insights are formally proved.

The 2 nd  and 3 rd  stages of insight learning are well described in anecdotes of famous scientific breakthroughs. In 1861, August Kekulé was contemplating the structure of the Benzene molecule. He knew it was a chain of 6 carbon atoms attached to 6 hydrogen atoms. Still, He got stuck   (incubation phase)  on working out how they could fit together to remain chemically stable.

He turned away from his desk and, facing the fireplace, fell asleep. He dreamt of a snake eating its tail and then spinning around. He woke up and realized (insight phase)  that these carbon-hydrogen chains can close onto themselves to form hexagonal rings. He then worked out the consequences of his new insight on Benzene rings. (Verification phase)

Suitably prepared minds can experience insights while observing ordinary day-to-day events. Many people must have seen apples fall from trees and thought nothing of it. When Newton saw an apple fall, he connected its fall to the action of the moon. If an unseen force pulls the apple from the tree top, couldn't the same force extends to the moon? This same force must be keeping the moon tethered in orbit around the earth, keeping it from whizzing off into space. Of course, this seems counterintuitive because if the moon is like the apple, should it not be crashing down to earth?

Newton's prepared mind understood the moon to be continuously falling to earth around the horizon's curve. Earth's gravitational pull on the moon balanced its horizontal velocity tangential to its orbit. If the apple were shot fast enough over the horizon from a cannon, it too, like the moon, would stay in orbit.

So, although before Newton, everyone was aware of gravity in a stimulus-response kind of way and even made practical use of it to weigh things, no one understood its universal implications.

Applying Insight Learning To The Classroom

The preparation-incubation-insight- verification cycle could be implemented by teachers in the classroom. Gestalt theory predicts that students learn best when they engage with the material; they are mentally prepared  for age, and maturity, having had experiences enabling them to relate to the material and having background knowledge that allows them to contextualize the material. When first presenting content they want to teach the students, teachers must make sure students are suitably prepared to receive the material, to successfully go through the preparation stage of learning.

Teachers should present the material holistically and contextually. For example, when teaching about the human heart, they should also teach where it is in the human body and its functional importance and relationship to other organs and parts of the body. Teachers could also connect other fields, such as comparing hearts to mechanical pumps.

Once the teacher has imparted sufficient background information to students, they should set a problem for their students to solve independently or in groups. The problem should require the students to apply what they have learned in a new way and make novel connections not explicitly made by the teacher during the lesson.

However, they must already know and be familiar with all the material they need to solve the problem. Students must be allowed to fumble their way to a solution  and make many mistakes , as this is vital for the incubation phase. The teacher should resist the temptation to spoon-feed them. Instead, teachers should use the Socratic method to coax the students into arriving at solutions and answers themselves.

Allowing the students to go through a sufficiently challenging incubation phase engages all their higher cognitive functions, such as logical and abstract reasoning, visualization, and imagination. It also habituates them to a bit of frustration to build the mental toughness to stay focused.

It also forces their brains to work hard in processing combining information to sufficiently own the insights they achieve, making it more likely that they will retain  the knowledge they gained and be able to apply it across different contexts.

Once students have written down their insights and solutions, the teacher should guide them through the verification phase. The teacher and students need to check and test the validity of the answers. Solutions should be checked for errors and inconsistencies and checked against the norms and standards of the field.

However, one should remember that mass education is aimed at students of average capacity and that not all students are always equally capable of learning through insight. Also, students need to be prepared to gain the ability and potential to have fruitful insights.  

Learning purely from stimulus-response conditioning is insufficient for progress and major breakthroughs to be made in the sciences. For breakthroughs to be made, humans need to be increasingly capable of higher and higher levels of abstract thinking.

However, we are not all equally capable of having epiphanies on the cutting edge of scientific research. Most education aims to elevate average reasoning, knowledge, and skill acquisition. For insight, learning must build on rather than replace behaviorist teaching practices.

Related posts:

• The Psychology of Long Distance Relationships
• Beck’s Depression Inventory (BDI Test)
• Operant Conditioning (Examples + Research)
• Variable Interval Reinforcement Schedule (Examples)
• Concrete Operational Stage (3rd Cognitive Development)

Reference this article:

About The Author

Operant Conditioning

Classical Conditioning

Observational Learning

Latent Learning

Experiential Learning

The Little Albert Study

Bobo Doll Experiment

Spacing Effect

Von Restorff Effect

PracticalPie.com is a participant in the Amazon Associates Program. As an Amazon Associate we earn from qualifying purchases.

Follow Us On:

Youtube Facebook Instagram X/Twitter

Psychology Resources

Developmental

Personality

Relationships

Psychologists

Serial Killers

Psychology Tests

Personality Quiz

Memory Test

Depression test

Type A/B Personality Test

© PracticalPsychology. All rights reserved

Privacy Policy | Terms of Use

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Module 7: Thinking, Reasoning, and Problem-Solving

This module is about how a solid working knowledge of psychological principles can help you to think more effectively, so you can succeed in school and life. You might be inclined to believe that—because you have been thinking for as long as you can remember, because you are able to figure out the solution to many problems, because you feel capable of using logic to argue a point, because you can evaluate whether the things you read and hear make sense—you do not need any special training in thinking. But this, of course, is one of the key barriers to helping people think better. If you do not believe that there is anything wrong, why try to fix it?

The human brain is indeed a remarkable thinking machine, capable of amazing, complex, creative, logical thoughts. Why, then, are we telling you that you need to learn how to think? Mainly because one major lesson from cognitive psychology is that these capabilities of the human brain are relatively infrequently realized. Many psychologists believe that people are essentially “cognitive misers.” It is not that we are lazy, but that we have a tendency to expend the least amount of mental effort necessary. Although you may not realize it, it actually takes a great deal of energy to think. Careful, deliberative reasoning and critical thinking are very difficult. Because we seem to be successful without going to the trouble of using these skills well, it feels unnecessary to develop them. As you shall see, however, there are many pitfalls in the cognitive processes described in this module. When people do not devote extra effort to learning and improving reasoning, problem solving, and critical thinking skills, they make many errors.

As is true for memory, if you develop the cognitive skills presented in this module, you will be more successful in school. It is important that you realize, however, that these skills will help you far beyond school, even more so than a good memory will. Although it is somewhat useful to have a good memory, ten years from now no potential employer will care how many questions you got right on multiple choice exams during college. All of them will, however, recognize whether you are a logical, analytical, critical thinker. With these thinking skills, you will be an effective, persuasive communicator and an excellent problem solver.

The module begins by describing different kinds of thought and knowledge, especially conceptual knowledge and critical thinking. An understanding of these differences will be valuable as you progress through school and encounter different assignments that require you to tap into different kinds of knowledge. The second section covers deductive and inductive reasoning, which are processes we use to construct and evaluate strong arguments. They are essential skills to have whenever you are trying to persuade someone (including yourself) of some point, or to respond to someone’s efforts to persuade you. The module ends with a section about problem solving. A solid understanding of the key processes involved in problem solving will help you to handle many daily challenges.

7.1. Different kinds of thought

7.2. Reasoning and Judgment

7.3. Problem Solving

READING WITH PURPOSE

Remember and understand.

By reading and studying Module 7, you should be able to remember and describe:

• Concepts and inferences (7.1)
• Procedural knowledge (7.1)
• Metacognition (7.1)
• Characteristics of critical thinking:  skepticism; identify biases, distortions, omissions, and assumptions; reasoning and problem solving skills  (7.1)
• Reasoning:  deductive reasoning, deductively valid argument, inductive reasoning, inductively strong argument, availability heuristic, representativeness heuristic  (7.2)
• Fixation:  functional fixedness, mental set  (7.3)
• Algorithms, heuristics, and the role of confirmation bias (7.3)
• Effective problem solving sequence (7.3)

By reading and thinking about how the concepts in Module 6 apply to real life, you should be able to:

• Identify which type of knowledge a piece of information is (7.1)
• Recognize examples of deductive and inductive reasoning (7.2)
• Recognize judgments that have probably been influenced by the availability heuristic (7.2)
• Recognize examples of problem solving heuristics and algorithms (7.3)

Analyze, Evaluate, and Create

By reading and thinking about Module 6, participating in classroom activities, and completing out-of-class assignments, you should be able to:

• Use the principles of critical thinking to evaluate information (7.1)
• Explain whether examples of reasoning arguments are deductively valid or inductively strong (7.2)
• Outline how you could try to solve a problem from your life using the effective problem solving sequence (7.3)

7.1. Different kinds of thought and knowledge

• Take a few minutes to write down everything that you know about dogs.
• Do you believe that:
• Psychic ability exists?
• Hypnosis is an altered state of consciousness?
• Magnet therapy is effective for relieving pain?
• Aerobic exercise is an effective treatment for depression?
• UFO’s from outer space have visited earth?

On what do you base your belief or disbelief for the questions above?

Of course, we all know what is meant by the words  think  and  knowledge . You probably also realize that they are not unitary concepts; there are different kinds of thought and knowledge. In this section, let us look at some of these differences. If you are familiar with these different kinds of thought and pay attention to them in your classes, it will help you to focus on the right goals, learn more effectively, and succeed in school. Different assignments and requirements in school call on you to use different kinds of knowledge or thought, so it will be very helpful for you to learn to recognize them (Anderson, et al. 2001).

Factual and conceptual knowledge

Module 5 introduced the idea of declarative memory, which is composed of facts and episodes. If you have ever played a trivia game or watched Jeopardy on TV, you realize that the human brain is able to hold an extraordinary number of facts. Likewise, you realize that each of us has an enormous store of episodes, essentially facts about events that happened in our own lives. It may be difficult to keep that in mind when we are struggling to retrieve one of those facts while taking an exam, however. Part of the problem is that, in contradiction to the advice from Module 5, many students continue to try to memorize course material as a series of unrelated facts (picture a history student simply trying to memorize history as a set of unrelated dates without any coherent story tying them together). Facts in the real world are not random and unorganized, however. It is the way that they are organized that constitutes a second key kind of knowledge, conceptual.

Concepts are nothing more than our mental representations of categories of things in the world. For example, think about dogs. When you do this, you might remember specific facts about dogs, such as they have fur and they bark. You may also recall dogs that you have encountered and picture them in your mind. All of this information (and more) makes up your concept of dog. You can have concepts of simple categories (e.g., triangle), complex categories (e.g., small dogs that sleep all day, eat out of the garbage, and bark at leaves), kinds of people (e.g., psychology professors), events (e.g., birthday parties), and abstract ideas (e.g., justice). Gregory Murphy (2002) refers to concepts as the “glue that holds our mental life together” (p. 1). Very simply, summarizing the world by using concepts is one of the most important cognitive tasks that we do. Our conceptual knowledge  is  our knowledge about the world. Individual concepts are related to each other to form a rich interconnected network of knowledge. For example, think about how the following concepts might be related to each other: dog, pet, play, Frisbee, chew toy, shoe. Or, of more obvious use to you now, how these concepts are related: working memory, long-term memory, declarative memory, procedural memory, and rehearsal? Because our minds have a natural tendency to organize information conceptually, when students try to remember course material as isolated facts, they are working against their strengths.

One last important point about concepts is that they allow you to instantly know a great deal of information about something. For example, if someone hands you a small red object and says, “here is an apple,” they do not have to tell you, “it is something you can eat.” You already know that you can eat it because it is true by virtue of the fact that the object is an apple; this is called drawing an  inference , assuming that something is true on the basis of your previous knowledge (for example, of category membership or of how the world works) or logical reasoning.

Procedural knowledge

Physical skills, such as tying your shoes, doing a cartwheel, and driving a car (or doing all three at the same time, but don’t try this at home) are certainly a kind of knowledge. They are procedural knowledge, the same idea as procedural memory that you saw in Module 5. Mental skills, such as reading, debating, and planning a psychology experiment, are procedural knowledge, as well. In short, procedural knowledge is the knowledge how to do something (Cohen & Eichenbaum, 1993).

Metacognitive knowledge

Floyd used to think that he had a great memory. Now, he has a better memory. Why? Because he finally realized that his memory was not as great as he once thought it was. Because Floyd eventually learned that he often forgets where he put things, he finally developed the habit of putting things in the same place. (Unfortunately, he did not learn this lesson before losing at least 5 watches and a wedding ring.) Because he finally realized that he often forgets to do things, he finally started using the To Do list app on his phone. And so on. Floyd’s insights about the real limitations of his memory have allowed him to remember things that he used to forget.

All of us have knowledge about the way our own minds work. You may know that you have a good memory for people’s names and a poor memory for math formulas. Someone else might realize that they have difficulty remembering to do things, like stopping at the store on the way home. Others still know that they tend to overlook details. This knowledge about our own thinking is actually quite important; it is called metacognitive knowledge, or  metacognition . Like other kinds of thinking skills, it is subject to error. For example, in unpublished research, one of the authors surveyed about 120 General Psychology students on the first day of the term. Among other questions, the students were asked them to predict their grade in the class and report their current Grade Point Average. Two-thirds of the students predicted that their grade in the course would be higher than their GPA. (The reality is that at our college, students tend to earn lower grades in psychology than their overall GPA.) Another example: Students routinely report that they thought they had done well on an exam, only to discover, to their dismay, that they were wrong (more on that important problem in a moment). Both errors reveal a breakdown in metacognition.

The Dunning-Kruger Effect

In general, most college students probably do not study enough. For example, using data from the National Survey of Student Engagement, Fosnacht, McCormack, and Lerma (2018) reported that first-year students at 4-year colleges in the U.S. averaged less than 14 hours per week preparing for classes. The typical suggestion is that you should spend two hours outside of class for every hour in class, or 24 – 30 hours per week for a full-time student. Clearly, students in general are nowhere near that recommended mark. Many observers, including some faculty, believe that this shortfall is a result of students being too busy or lazy. Now, it may be true that many students are too busy, with work and family obligations, for example. Others, are not particularly motivated in school, and therefore might correctly be labeled lazy. A third possible explanation, however, is that some students might not think they need to spend this much time. And this is a matter of metacognition. Consider the scenario that we mentioned above, students thinking they had done well on an exam only to discover that they did not. Justin Kruger and David Dunning examined scenarios very much like this in 1999. Kruger and Dunning gave research participants tests measuring humor, logic, and grammar. Then, they asked the participants to assess their own abilities and test performance in these areas. They found that participants in general tended to overestimate their abilities, already a problem with metacognition. Importantly, the participants who scored the lowest overestimated their abilities the most. Specifically, students who scored in the bottom quarter (averaging in the 12th percentile) thought they had scored in the 62nd percentile. This has become known as the  Dunning-Kruger effect . Many individual faculty members have replicated these results with their own student on their course exams, including the authors of this book. Think about it. Some students who just took an exam and performed poorly believe that they did well before seeing their score. It seems very likely that these are the very same students who stopped studying the night before because they thought they were “done.” Quite simply, it is not just that they did not know the material. They did not know that they did not know the material. That is poor metacognition.

In order to develop good metacognitive skills, you should continually monitor your thinking and seek frequent feedback on the accuracy of your thinking (Medina, Castleberry, & Persky 2017). For example, in classes get in the habit of predicting your exam grades. As soon as possible after taking an exam, try to find out which questions you missed and try to figure out why. If you do this soon enough, you may be able to recall the way it felt when you originally answered the question. Did you feel confident that you had answered the question correctly? Then you have just discovered an opportunity to improve your metacognition. Be on the lookout for that feeling and respond with caution.

concept :  a mental representation of a category of things in the world

Dunning-Kruger effect : individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

inference : an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

metacognition :  knowledge about one’s own cognitive processes; thinking about your thinking

Critical thinking

One particular kind of knowledge or thinking skill that is related to metacognition is  critical thinking (Chew, 2020). You may have noticed that critical thinking is an objective in many college courses, and thus it could be a legitimate topic to cover in nearly any college course. It is particularly appropriate in psychology, however. As the science of (behavior and) mental processes, psychology is obviously well suited to be the discipline through which you should be introduced to this important way of thinking.

More importantly, there is a particular need to use critical thinking in psychology. We are all, in a way, experts in human behavior and mental processes, having engaged in them literally since birth. Thus, perhaps more than in any other class, students typically approach psychology with very clear ideas and opinions about its subject matter. That is, students already “know” a lot about psychology. The problem is, “it ain’t so much the things we don’t know that get us into trouble. It’s the things we know that just ain’t so” (Ward, quoted in Gilovich 1991). Indeed, many of students’ preconceptions about psychology are just plain wrong. Randolph Smith (2002) wrote a book about critical thinking in psychology called  Challenging Your Preconceptions,  highlighting this fact. On the other hand, many of students’ preconceptions about psychology are just plain right! But wait, how do you know which of your preconceptions are right and which are wrong? And when you come across a research finding or theory in this class that contradicts your preconceptions, what will you do? Will you stick to your original idea, discounting the information from the class? Will you immediately change your mind? Critical thinking can help us sort through this confusing mess.

But what is critical thinking? The goal of critical thinking is simple to state (but extraordinarily difficult to achieve): it is to be right, to draw the correct conclusions, to believe in things that are true and to disbelieve things that are false. We will provide two definitions of critical thinking (or, if you like, one large definition with two distinct parts). First, a more conceptual one: Critical thinking is thinking like a scientist in your everyday life (Schmaltz, Jansen, & Wenckowski, 2017).  Our second definition is more operational; it is simply a list of skills that are essential to be a critical thinker. Critical thinking entails solid reasoning and problem solving skills; skepticism; and an ability to identify biases, distortions, omissions, and assumptions. Excellent deductive and inductive reasoning, and problem solving skills contribute to critical thinking. So, you can consider the subject matter of sections 7.2 and 7.3 to be part of critical thinking. Because we will be devoting considerable time to these concepts in the rest of the module, let us begin with a discussion about the other aspects of critical thinking.

Let’s address that first part of the definition. Scientists form hypotheses, or predictions about some possible future observations. Then, they collect data, or information (think of this as making those future observations). They do their best to make unbiased observations using reliable techniques that have been verified by others. Then, and only then, they draw a conclusion about what those observations mean. Oh, and do not forget the most important part. “Conclusion” is probably not the most appropriate word because this conclusion is only tentative. A scientist is always prepared that someone else might come along and produce new observations that would require a new conclusion be drawn. Wow! If you like to be right, you could do a lot worse than using a process like this.

A Critical Thinker’s Toolkit 

Now for the second part of the definition. Good critical thinkers (and scientists) rely on a variety of tools to evaluate information. Perhaps the most recognizable tool for critical thinking is  skepticism (and this term provides the clearest link to the thinking like a scientist definition, as you are about to see). Some people intend it as an insult when they call someone a skeptic. But if someone calls you a skeptic, if they are using the term correctly, you should consider it a great compliment. Simply put, skepticism is a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided. People from Missouri should recognize this principle, as Missouri is known as the Show-Me State. As a skeptic, you are not inclined to believe something just because someone said so, because someone else believes it, or because it sounds reasonable. You must be persuaded by high quality evidence.

Of course, if that evidence is produced, you have a responsibility as a skeptic to change your belief. Failure to change a belief in the face of good evidence is not skepticism; skepticism has open mindedness at its core. M. Neil Browne and Stuart Keeley (2018) use the term weak sense critical thinking to describe critical thinking behaviors that are used only to strengthen a prior belief. Strong sense critical thinking, on the other hand, has as its goal reaching the best conclusion. Sometimes that means strengthening your prior belief, but sometimes it means changing your belief to accommodate the better evidence.

Many times, a failure to think critically or weak sense critical thinking is related to a  bias , an inclination, tendency, leaning, or prejudice. Everybody has biases, but many people are unaware of them. Awareness of your own biases gives you the opportunity to control or counteract them. Unfortunately, however, many people are happy to let their biases creep into their attempts to persuade others; indeed, it is a key part of their persuasive strategy. To see how these biases influence messages, just look at the different descriptions and explanations of the same events given by people of different ages or income brackets, or conservative versus liberal commentators, or by commentators from different parts of the world. Of course, to be successful, these people who are consciously using their biases must disguise them. Even undisguised biases can be difficult to identify, so disguised ones can be nearly impossible.

Here are some common sources of biases:

• Personal values and beliefs.  Some people believe that human beings are basically driven to seek power and that they are typically in competition with one another over scarce resources. These beliefs are similar to the world-view that political scientists call “realism.” Other people believe that human beings prefer to cooperate and that, given the chance, they will do so. These beliefs are similar to the world-view known as “idealism.” For many people, these deeply held beliefs can influence, or bias, their interpretations of such wide ranging situations as the behavior of nations and their leaders or the behavior of the driver in the car ahead of you. For example, if your worldview is that people are typically in competition and someone cuts you off on the highway, you may assume that the driver did it purposely to get ahead of you. Other types of beliefs about the way the world is or the way the world should be, for example, political beliefs, can similarly become a significant source of bias.
• Racism, sexism, ageism and other forms of prejudice and bigotry.  These are, sadly, a common source of bias in many people. They are essentially a special kind of “belief about the way the world is.” These beliefs—for example, that women do not make effective leaders—lead people to ignore contradictory evidence (examples of effective women leaders, or research that disputes the belief) and to interpret ambiguous evidence in a way consistent with the belief.
• Self-interest.  When particular people benefit from things turning out a certain way, they can sometimes be very susceptible to letting that interest bias them. For example, a company that will earn a profit if they sell their product may have a bias in the way that they give information about their product. A union that will benefit if its members get a generous contract might have a bias in the way it presents information about salaries at competing organizations. (Note that our inclusion of examples describing both companies and unions is an explicit attempt to control for our own personal biases). Home buyers are often dismayed to discover that they purchased their dream house from someone whose self-interest led them to lie about flooding problems in the basement or back yard. This principle, the biasing power of self-interest, is likely what led to the famous phrase  Caveat Emptor  (let the buyer beware) .  

Knowing that these types of biases exist will help you evaluate evidence more critically. Do not forget, though, that people are not always keen to let you discover the sources of biases in their arguments. For example, companies or political organizations can sometimes disguise their support of a research study by contracting with a university professor, who comes complete with a seemingly unbiased institutional affiliation, to conduct the study.

People’s biases, conscious or unconscious, can lead them to make omissions, distortions, and assumptions that undermine our ability to correctly evaluate evidence. It is essential that you look for these elements. Always ask, what is missing, what is not as it appears, and what is being assumed here? For example, consider this (fictional) chart from an ad reporting customer satisfaction at 4 local health clubs.

Clearly, from the results of the chart, one would be tempted to give Club C a try, as customer satisfaction is much higher than for the other 3 clubs.

There are so many distortions and omissions in this chart, however, that it is actually quite meaningless. First, how was satisfaction measured? Do the bars represent responses to a survey? If so, how were the questions asked? Most importantly, where is the missing scale for the chart? Although the differences look quite large, are they really?

Well, here is the same chart, with a different scale, this time labeled:

Club C is not so impressive any more, is it? In fact, all of the health clubs have customer satisfaction ratings (whatever that means) between 85% and 88%. In the first chart, the entire scale of the graph included only the percentages between 83 and 89. This “judicious” choice of scale—some would call it a distortion—and omission of that scale from the chart make the tiny differences among the clubs seem important, however.

Also, in order to be a critical thinker, you need to learn to pay attention to the assumptions that underlie a message. Let us briefly illustrate the role of assumptions by touching on some people’s beliefs about the criminal justice system in the US. Some believe that a major problem with our judicial system is that many criminals go free because of legal technicalities. Others believe that a major problem is that many innocent people are convicted of crimes. The simple fact is, both types of errors occur. A person’s conclusion about which flaw in our judicial system is the greater tragedy is based on an assumption about which of these is the more serious error (letting the guilty go free or convicting the innocent). This type of assumption is called a value assumption (Browne and Keeley, 2018). It reflects the differences in values that people develop, differences that may lead us to disregard valid evidence that does not fit in with our particular values.

Oh, by the way, some students probably noticed this, but the seven tips for evaluating information that we shared in Module 1 are related to this. Actually, they are part of this section. The tips are, to a very large degree, set of ideas you can use to help you identify biases, distortions, omissions, and assumptions. If you do not remember this section, we strongly recommend you take a few minutes to review it.

skepticism :  a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

bias : an inclination, tendency, leaning, or prejudice

• Which of your beliefs (or disbeliefs) from the Activate exercise for this section were derived from a process of critical thinking? If some of your beliefs were not based on critical thinking, are you willing to reassess these beliefs? If the answer is no, why do you think that is? If the answer is yes, what concrete steps will you take?

7.2 Reasoning and Judgment

• What percentage of kidnappings are committed by strangers?
• Which area of the house is riskiest: kitchen, bathroom, or stairs?
• What is the most common cancer in the US?
• What percentage of workplace homicides are committed by co-workers?

An essential set of procedural thinking skills is  reasoning , the ability to generate and evaluate solid conclusions from a set of statements or evidence. You should note that these conclusions (when they are generated instead of being evaluated) are one key type of inference that we described in Section 7.1. There are two main types of reasoning, deductive and inductive.

Deductive reasoning

Suppose your teacher tells you that if you get an A on the final exam in a course, you will get an A for the whole course. Then, you get an A on the final exam. What will your final course grade be? Most people can see instantly that you can conclude with certainty that you will get an A for the course. This is a type of reasoning called  deductive reasoning , which is defined as reasoning in which a conclusion is guaranteed to be true as long as the statements leading to it are true. The three statements can be listed as an  argument , with two beginning statements and a conclusion:

Statement 1: If you get an A on the final exam, you will get an A for the course

Statement 2: You get an A on the final exam

Conclusion: You will get an A for the course

This particular arrangement, in which true beginning statements lead to a guaranteed true conclusion, is known as a  deductively valid argument . Although deductive reasoning is often the subject of abstract, brain-teasing, puzzle-like word problems, it is actually an extremely important type of everyday reasoning. It is just hard to recognize sometimes. For example, imagine that you are looking for your car keys and you realize that they are either in the kitchen drawer or in your book bag. After looking in the kitchen drawer, you instantly know that they must be in your book bag. That conclusion results from a simple deductive reasoning argument. In addition, solid deductive reasoning skills are necessary for you to succeed in the sciences, philosophy, math, computer programming, and any endeavor involving the use of logic to persuade others to your point of view or to evaluate others’ arguments.

Cognitive psychologists, and before them philosophers, have been quite interested in deductive reasoning, not so much for its practical applications, but for the insights it can offer them about the ways that human beings think. One of the early ideas to emerge from the examination of deductive reasoning is that people learn (or develop) mental versions of rules that allow them to solve these types of reasoning problems (Braine, 1978; Braine, Reiser, & Rumain, 1984). The best way to see this point of view is to realize that there are different possible rules, and some of them are very simple. For example, consider this rule of logic:

therefore q

Logical rules are often presented abstractly, as letters, in order to imply that they can be used in very many specific situations. Here is a concrete version of the of the same rule:

I’ll either have pizza or a hamburger for dinner tonight (p or q)

I won’t have pizza (not p)

Therefore, I’ll have a hamburger (therefore q)

This kind of reasoning seems so natural, so easy, that it is quite plausible that we would use a version of this rule in our daily lives. At least, it seems more plausible than some of the alternative possibilities—for example, that we need to have experience with the specific situation (pizza or hamburger, in this case) in order to solve this type of problem easily. So perhaps there is a form of natural logic (Rips, 1990) that contains very simple versions of logical rules. When we are faced with a reasoning problem that maps onto one of these rules, we use the rule.

But be very careful; things are not always as easy as they seem. Even these simple rules are not so simple. For example, consider the following rule. Many people fail to realize that this rule is just as valid as the pizza or hamburger rule above.

if p, then q

therefore, not p

Concrete version:

If I eat dinner, then I will have dessert

I did not have dessert

Therefore, I did not eat dinner

The simple fact is, it can be very difficult for people to apply rules of deductive logic correctly; as a result, they make many errors when trying to do so. Is this a deductively valid argument or not?

Students who like school study a lot

Students who study a lot get good grades

Jane does not like school

Therefore, Jane does not get good grades

Many people are surprised to discover that this is not a logically valid argument; the conclusion is not guaranteed to be true from the beginning statements. Although the first statement says that students who like school study a lot, it does NOT say that students who do not like school do not study a lot. In other words, it may very well be possible to study a lot without liking school. Even people who sometimes get problems like this right might not be using the rules of deductive reasoning. Instead, they might just be making judgments for examples they know, in this case, remembering instances of people who get good grades despite not liking school.

Making deductive reasoning even more difficult is the fact that there are two important properties that an argument may have. One, it can be valid or invalid (meaning that the conclusion does or does not follow logically from the statements leading up to it). Two, an argument (or more correctly, its conclusion) can be true or false. Here is an example of an argument that is logically valid, but has a false conclusion (at least we think it is false).

Either you are eleven feet tall or the Grand Canyon was created by a spaceship crashing into the earth.

You are not eleven feet tall

Therefore the Grand Canyon was created by a spaceship crashing into the earth

This argument has the exact same form as the pizza or hamburger argument above, making it is deductively valid. The conclusion is so false, however, that it is absurd (of course, the reason the conclusion is false is that the first statement is false). When people are judging arguments, they tend to not observe the difference between deductive validity and the empirical truth of statements or conclusions. If the elements of an argument happen to be true, people are likely to judge the argument logically valid; if the elements are false, they will very likely judge it invalid (Markovits & Bouffard-Bouchard, 1992; Moshman & Franks, 1986). Thus, it seems a stretch to say that people are using these logical rules to judge the validity of arguments. Many psychologists believe that most people actually have very limited deductive reasoning skills (Johnson-Laird, 1999). They argue that when faced with a problem for which deductive logic is required, people resort to some simpler technique, such as matching terms that appear in the statements and the conclusion (Evans, 1982). This might not seem like a problem, but what if reasoners believe that the elements are true and they happen to be wrong; they will would believe that they are using a form of reasoning that guarantees they are correct and yet be wrong.

deductive reasoning :  a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

argument :  a set of statements in which the beginning statements lead to a conclusion

deductively valid argument :  an argument for which true beginning statements guarantee that the conclusion is true

Inductive reasoning and judgment

Every day, you make many judgments about the likelihood of one thing or another. Whether you realize it or not, you are practicing  inductive reasoning   on a daily basis. In inductive reasoning arguments, a conclusion is likely whenever the statements preceding it are true. The first thing to notice about inductive reasoning is that, by definition, you can never be sure about your conclusion; you can only estimate how likely the conclusion is. Inductive reasoning may lead you to focus on Memory Encoding and Recoding when you study for the exam, but it is possible the instructor will ask more questions about Memory Retrieval instead. Unlike deductive reasoning, the conclusions you reach through inductive reasoning are only probable, not certain. That is why scientists consider inductive reasoning weaker than deductive reasoning. But imagine how hard it would be for us to function if we could not act unless we were certain about the outcome.

Inductive reasoning can be represented as logical arguments consisting of statements and a conclusion, just as deductive reasoning can be. In an inductive argument, you are given some statements and a conclusion (or you are given some statements and must draw a conclusion). An argument is  inductively strong   if the conclusion would be very probable whenever the statements are true. So, for example, here is an inductively strong argument:

• Statement #1: The forecaster on Channel 2 said it is going to rain today.
• Statement #2: The forecaster on Channel 5 said it is going to rain today.
• Statement #3: It is very cloudy and humid.
• Statement #4: You just heard thunder.
• Conclusion (or judgment): It is going to rain today.

Think of the statements as evidence, on the basis of which you will draw a conclusion. So, based on the evidence presented in the four statements, it is very likely that it will rain today. Will it definitely rain today? Certainly not. We can all think of times that the weather forecaster was wrong.

A true story: Some years ago psychology student was watching a baseball playoff game between the St. Louis Cardinals and the Los Angeles Dodgers. A graphic on the screen had just informed the audience that the Cardinal at bat, (Hall of Fame shortstop) Ozzie Smith, a switch hitter batting left-handed for this plate appearance, had never, in nearly 3000 career at-bats, hit a home run left-handed. The student, who had just learned about inductive reasoning in his psychology class, turned to his companion (a Cardinals fan) and smugly said, “It is an inductively strong argument that Ozzie Smith will not hit a home run.” He turned back to face the television just in time to watch the ball sail over the right field fence for a home run. Although the student felt foolish at the time, he was not wrong. It was an inductively strong argument; 3000 at-bats is an awful lot of evidence suggesting that the Wizard of Ozz (as he was known) would not be hitting one out of the park (think of each at-bat without a home run as a statement in an inductive argument). Sadly (for the die-hard Cubs fan and Cardinals-hating student), despite the strength of the argument, the conclusion was wrong.

Given the possibility that we might draw an incorrect conclusion even with an inductively strong argument, we really want to be sure that we do, in fact, make inductively strong arguments. If we judge something probable, it had better be probable. If we judge something nearly impossible, it had better not happen. Think of inductive reasoning, then, as making reasonably accurate judgments of the probability of some conclusion given a set of evidence.

We base many decisions in our lives on inductive reasoning. For example:

Statement #1: Psychology is not my best subject

Statement #2: My psychology instructor has a reputation for giving difficult exams

Statement #3: My first psychology exam was much harder than I expected

Judgment: The next exam will probably be very difficult.

Decision: I will study tonight instead of watching Netflix.

Some other examples of judgments that people commonly make in a school context include judgments of the likelihood that:

• A particular class will be interesting/useful/difficult
• You will be able to finish writing a paper by next week if you go out tonight
• Your laptop’s battery will last through the next trip to the library
• You will not miss anything important if you skip class tomorrow
• Your instructor will not notice if you skip class tomorrow
• You will be able to find a book that you will need for a paper
• There will be an essay question about Memory Encoding on the next exam

Tversky and Kahneman (1983) recognized that there are two general ways that we might make these judgments; they termed them extensional (i.e., following the laws of probability) and intuitive (i.e., using shortcuts or heuristics, see below). We will use a similar distinction between Type 1 and Type 2 thinking, as described by Keith Stanovich and his colleagues (Evans and Stanovich, 2013; Stanovich and West, 2000). Type 1 thinking is fast, automatic, effortful, and emotional. In fact, it is hardly fair to call it reasoning at all, as judgments just seem to pop into one’s head. Type 2 thinking , on the other hand, is slow, effortful, and logical. So obviously, it is more likely to lead to a correct judgment, or an optimal decision. The problem is, we tend to over-rely on Type 1. Now, we are not saying that Type 2 is the right way to go for every decision or judgment we make. It seems a bit much, for example, to engage in a step-by-step logical reasoning procedure to decide whether we will have chicken or fish for dinner tonight.

Many bad decisions in some very important contexts, however, can be traced back to poor judgments of the likelihood of certain risks or outcomes that result from the use of Type 1 when a more logical reasoning process would have been more appropriate. For example:

Statement #1: It is late at night.

Statement #2: Albert has been drinking beer for the past five hours at a party.

Statement #3: Albert is not exactly sure where he is or how far away home is.

Judgment: Albert will have no difficulty walking home.

Decision: He walks home alone.

As you can see in this example, the three statements backing up the judgment do not really support it. In other words, this argument is not inductively strong because it is based on judgments that ignore the laws of probability. What are the chances that someone facing these conditions will be able to walk home alone easily? And one need not be drunk to make poor decisions based on judgments that just pop into our heads.

The truth is that many of our probability judgments do not come very close to what the laws of probability say they should be. Think about it. In order for us to reason in accordance with these laws, we would need to know the laws of probability, which would allow us to calculate the relationship between particular pieces of evidence and the probability of some outcome (i.e., how much likelihood should change given a piece of evidence), and we would have to do these heavy math calculations in our heads. After all, that is what Type 2 requires. Needless to say, even if we were motivated, we often do not even know how to apply Type 2 reasoning in many cases.

So what do we do when we don’t have the knowledge, skills, or time required to make the correct mathematical judgment? Do we hold off and wait until we can get better evidence? Do we read up on probability and fire up our calculator app so we can compute the correct probability? Of course not. We rely on Type 1 thinking. We “wing it.” That is, we come up with a likelihood estimate using some means at our disposal. Psychologists use the term heuristic to describe the type of “winging it” we are talking about. A  heuristic   is a shortcut strategy that we use to make some judgment or solve some problem (see Section 7.3). Heuristics are easy and quick, think of them as the basic procedures that are characteristic of Type 1.  They can absolutely lead to reasonably good judgments and decisions in some situations (like choosing between chicken and fish for dinner). They are, however, far from foolproof. There are, in fact, quite a lot of situations in which heuristics can lead us to make incorrect judgments, and in many cases the decisions based on those judgments can have serious consequences.

Let us return to the activity that begins this section. You were asked to judge the likelihood (or frequency) of certain events and risks. You were free to come up with your own evidence (or statements) to make these judgments. This is where a heuristic crops up. As a judgment shortcut, we tend to generate specific examples of those very events to help us decide their likelihood or frequency. For example, if we are asked to judge how common, frequent, or likely a particular type of cancer is, many of our statements would be examples of specific cancer cases:

Statement #1: Andy Kaufman (comedian) had lung cancer.

Statement #2: Colin Powell (US Secretary of State) had prostate cancer.

Statement #3: Bob Marley (musician) had skin and brain cancer

Statement #4: Sandra Day O’Connor (Supreme Court Justice) had breast cancer.

Statement #5: Fred Rogers (children’s entertainer) had stomach cancer.

Statement #6: Robin Roberts (news anchor) had breast cancer.

Statement #7: Bette Davis (actress) had breast cancer.

Judgment: Breast cancer is the most common type.

Your own experience or memory may also tell you that breast cancer is the most common type. But it is not (although it is common). Actually, skin cancer is the most common type in the US. We make the same types of misjudgments all the time because we do not generate the examples or evidence according to their actual frequencies or probabilities. Instead, we have a tendency (or bias) to search for the examples in memory; if they are easy to retrieve, we assume that they are common. To rephrase this in the language of the heuristic, events seem more likely to the extent that they are available to memory. This bias has been termed the  availability heuristic   (Kahneman and Tversky, 1974).

The fact that we use the availability heuristic does not automatically mean that our judgment is wrong. The reason we use heuristics in the first place is that they work fairly well in many cases (and, of course that they are easy to use). So, the easiest examples to think of sometimes are the most common ones. Is it more likely that a member of the U.S. Senate is a man or a woman? Most people have a much easier time generating examples of male senators. And as it turns out, the U.S. Senate has many more men than women (74 to 26 in 2020). In this case, then, the availability heuristic would lead you to make the correct judgment; it is far more likely that a senator would be a man.

In many other cases, however, the availability heuristic will lead us astray. This is because events can be memorable for many reasons other than their frequency. Section 5.2, Encoding Meaning, suggested that one good way to encode the meaning of some information is to form a mental image of it. Thus, information that has been pictured mentally will be more available to memory. Indeed, an event that is vivid and easily pictured will trick many people into supposing that type of event is more common than it actually is. Repetition of information will also make it more memorable. So, if the same event is described to you in a magazine, on the evening news, on a podcast that you listen to, and in your Facebook feed; it will be very available to memory. Again, the availability heuristic will cause you to misperceive the frequency of these types of events.

Most interestingly, information that is unusual is more memorable. Suppose we give you the following list of words to remember: box, flower, letter, platypus, oven, boat, newspaper, purse, drum, car. Very likely, the easiest word to remember would be platypus, the unusual one. The same thing occurs with memories of events. An event may be available to memory because it is unusual, yet the availability heuristic leads us to judge that the event is common. Did you catch that? In these cases, the availability heuristic makes us think the exact opposite of the true frequency. We end up thinking something is common because it is unusual (and therefore memorable). Yikes.

The misapplication of the availability heuristic sometimes has unfortunate results. For example, if you went to K-12 school in the US over the past 10 years, it is extremely likely that you have participated in lockdown and active shooter drills. Of course, everyone is trying to prevent the tragedy of another school shooting. And believe us, we are not trying to minimize how terrible the tragedy is. But the truth of the matter is, school shootings are extremely rare. Because the federal government does not keep a database of school shootings, the Washington Post has maintained their own running tally. Between 1999 and January 2020 (the date of the most recent school shooting with a death in the US at of the time this paragraph was written), the Post reported a total of 254 people died in school shootings in the US. Not 254 per year, 254 total. That is an average of 12 per year. Of course, that is 254 people who should not have died (particularly because many were children), but in a country with approximately 60,000,000 students and teachers, this is a very small risk.

But many students and teachers are terrified that they will be victims of school shootings because of the availability heuristic. It is so easy to think of examples (they are very available to memory) that people believe the event is very common. It is not. And there is a downside to this. We happen to believe that there is an enormous gun violence problem in the United States. According the the Centers for Disease Control and Prevention, there were 39,773 firearm deaths in the US in 2017. Fifteen of those deaths were in school shootings, according to the Post. 60% of those deaths were suicides. When people pay attention to the school shooting risk (low), they often fail to notice the much larger risk.

And examples like this are by no means unique. The authors of this book have been teaching psychology since the 1990’s. We have been able to make the exact same arguments about the misapplication of the availability heuristics and keep them current by simply swapping out for the “fear of the day.” In the 1990’s it was children being kidnapped by strangers (it was known as “stranger danger”) despite the facts that kidnappings accounted for only 2% of the violent crimes committed against children, and only 24% of kidnappings are committed by strangers (US Department of Justice, 2007). This fear overlapped with the fear of terrorism that gripped the country after the 2001 terrorist attacks on the World Trade Center and US Pentagon and still plagues the population of the US somewhat in 2020. After a well-publicized, sensational act of violence, people are extremely likely to increase their estimates of the chances that they, too, will be victims of terror. Think about the reality, however. In October of 2001, a terrorist mailed anthrax spores to members of the US government and a number of media companies. A total of five people died as a result of this attack. The nation was nearly paralyzed by the fear of dying from the attack; in reality the probability of an individual person dying was 0.00000002.

The availability heuristic can lead you to make incorrect judgments in a school setting as well. For example, suppose you are trying to decide if you should take a class from a particular math professor. You might try to make a judgment of how good a teacher she is by recalling instances of friends and acquaintances making comments about her teaching skill. You may have some examples that suggest that she is a poor teacher very available to memory, so on the basis of the availability heuristic you judge her a poor teacher and decide to take the class from someone else. What if, however, the instances you recalled were all from the same person, and this person happens to be a very colorful storyteller? The subsequent ease of remembering the instances might not indicate that the professor is a poor teacher after all.

Although the availability heuristic is obviously important, it is not the only judgment heuristic we use. Amos Tversky and Daniel Kahneman examined the role of heuristics in inductive reasoning in a long series of studies. Kahneman received a Nobel Prize in Economics for this research in 2002, and Tversky would have certainly received one as well if he had not died of melanoma at age 59 in 1996 (Nobel Prizes are not awarded posthumously). Kahneman and Tversky demonstrated repeatedly that people do not reason in ways that are consistent with the laws of probability. They identified several heuristic strategies that people use instead to make judgments about likelihood. The importance of this work for economics (and the reason that Kahneman was awarded the Nobel Prize) is that earlier economic theories had assumed that people do make judgments rationally, that is, in agreement with the laws of probability.

Another common heuristic that people use for making judgments is the  representativeness heuristic (Kahneman & Tversky 1973). Suppose we describe a person to you. He is quiet and shy, has an unassuming personality, and likes to work with numbers. Is this person more likely to be an accountant or an attorney? If you said accountant, you were probably using the representativeness heuristic. Our imaginary person is judged likely to be an accountant because he resembles, or is representative of the concept of, an accountant. When research participants are asked to make judgments such as these, the only thing that seems to matter is the representativeness of the description. For example, if told that the person described is in a room that contains 70 attorneys and 30 accountants, participants will still assume that he is an accountant.

inductive reasoning :  a type of reasoning in which we make judgments about likelihood from sets of evidence

inductively strong argument :  an inductive argument in which the beginning statements lead to a conclusion that is probably true

heuristic :  a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

availability heuristic :  judging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

representativeness heuristic:   judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

Type 1 thinking : fast, automatic, and emotional thinking.

Type 2 thinking : slow, effortful, and logical thinking.

• What percentage of workplace homicides are co-worker violence?

Many people get these questions wrong. The answers are 10%; stairs; skin; 6%. How close were your answers? Explain how the availability heuristic might have led you to make the incorrect judgments.

• Can you think of some other judgments that you have made (or beliefs that you have) that might have been influenced by the availability heuristic?

7.3 Problem Solving

• Please take a few minutes to list a number of problems that you are facing right now.
• Now write about a problem that you recently solved.
• What is your definition of a problem?

Mary has a problem. Her daughter, ordinarily quite eager to please, appears to delight in being the last person to do anything. Whether getting ready for school, going to piano lessons or karate class, or even going out with her friends, she seems unwilling or unable to get ready on time. Other people have different kinds of problems. For example, many students work at jobs, have numerous family commitments, and are facing a course schedule full of difficult exams, assignments, papers, and speeches. How can they find enough time to devote to their studies and still fulfill their other obligations? Speaking of students and their problems: Show that a ball thrown vertically upward with initial velocity v0 takes twice as much time to return as to reach the highest point (from Spiegel, 1981).

These are three very different situations, but we have called them all problems. What makes them all the same, despite the differences? A psychologist might define a  problem   as a situation with an initial state, a goal state, and a set of possible intermediate states. Somewhat more meaningfully, we might consider a problem a situation in which you are in here one state (e.g., daughter is always late), you want to be there in another state (e.g., daughter is not always late), and with no obvious way to get from here to there. Defined this way, each of the three situations we outlined can now be seen as an example of the same general concept, a problem. At this point, you might begin to wonder what is not a problem, given such a general definition. It seems that nearly every non-routine task we engage in could qualify as a problem. As long as you realize that problems are not necessarily bad (it can be quite fun and satisfying to rise to the challenge and solve a problem), this may be a useful way to think about it.

Can we identify a set of problem-solving skills that would apply to these very different kinds of situations? That task, in a nutshell, is a major goal of this section. Let us try to begin to make sense of the wide variety of ways that problems can be solved with an important observation: the process of solving problems can be divided into two key parts. First, people have to notice, comprehend, and represent the problem properly in their minds (called  problem representation ). Second, they have to apply some kind of solution strategy to the problem. Psychologists have studied both of these key parts of the process in detail.

When you first think about the problem-solving process, you might guess that most of our difficulties would occur because we are failing in the second step, the application of strategies. Although this can be a significant difficulty much of the time, the more important source of difficulty is probably problem representation. In short, we often fail to solve a problem because we are looking at it, or thinking about it, the wrong way.

problem :  a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

problem representation :  noticing, comprehending and forming a mental conception of a problem

Defining and Mentally Representing Problems in Order to Solve Them

So, the main obstacle to solving a problem is that we do not clearly understand exactly what the problem is. Recall the problem with Mary’s daughter always being late. One way to represent, or to think about, this problem is that she is being defiant. She refuses to get ready in time. This type of representation or definition suggests a particular type of solution. Another way to think about the problem, however, is to consider the possibility that she is simply being sidetracked by interesting diversions. This different conception of what the problem is (i.e., different representation) suggests a very different solution strategy. For example, if Mary defines the problem as defiance, she may be tempted to solve the problem using some kind of coercive tactics, that is, to assert her authority as her mother and force her to listen. On the other hand, if Mary defines the problem as distraction, she may try to solve it by simply removing the distracting objects.

As you might guess, when a problem is represented one way, the solution may seem very difficult, or even impossible. Seen another way, the solution might be very easy. For example, consider the following problem (from Nasar, 1998):

Two bicyclists start 20 miles apart and head toward each other, each going at a steady rate of 10 miles per hour. At the same time, a fly that travels at a steady 15 miles per hour starts from the front wheel of the southbound bicycle and flies to the front wheel of the northbound one, then turns around and flies to the front wheel of the southbound one again, and continues in this manner until he is crushed between the two front wheels. Question: what total distance did the fly cover?

Please take a few minutes to try to solve this problem.

Most people represent this problem as a question about a fly because, well, that is how the question is asked. The solution, using this representation, is to figure out how far the fly travels on the first leg of its journey, then add this total to how far it travels on the second leg of its journey (when it turns around and returns to the first bicycle), then continue to add the smaller distance from each leg of the journey until you converge on the correct answer. You would have to be quite skilled at math to solve this problem, and you would probably need some time and pencil and paper to do it.

If you consider a different representation, however, you can solve this problem in your head. Instead of thinking about it as a question about a fly, think about it as a question about the bicycles. They are 20 miles apart, and each is traveling 10 miles per hour. How long will it take for the bicycles to reach each other? Right, one hour. The fly is traveling 15 miles per hour; therefore, it will travel a total of 15 miles back and forth in the hour before the bicycles meet. Represented one way (as a problem about a fly), the problem is quite difficult. Represented another way (as a problem about two bicycles), it is easy. Changing your representation of a problem is sometimes the best—sometimes the only—way to solve it.

Unfortunately, however, changing a problem’s representation is not the easiest thing in the world to do. Often, problem solvers get stuck looking at a problem one way. This is called  fixation . Most people who represent the preceding problem as a problem about a fly probably do not pause to reconsider, and consequently change, their representation. A parent who thinks her daughter is being defiant is unlikely to consider the possibility that her behavior is far less purposeful.

Problem-solving fixation was examined by a group of German psychologists called Gestalt psychologists during the 1930’s and 1940’s. Karl Dunker, for example, discovered an important type of failure to take a different perspective called  functional fixedness . Imagine being a participant in one of his experiments. You are asked to figure out how to mount two candles on a door and are given an assortment of odds and ends, including a small empty cardboard box and some thumbtacks. Perhaps you have already figured out a solution: tack the box to the door so it forms a platform, then put the candles on top of the box. Most people are able to arrive at this solution. Imagine a slight variation of the procedure, however. What if, instead of being empty, the box had matches in it? Most people given this version of the problem do not arrive at the solution given above. Why? Because it seems to people that when the box contains matches, it already has a function; it is a matchbox. People are unlikely to consider a new function for an object that already has a function. This is functional fixedness.

Mental set is a type of fixation in which the problem solver gets stuck using the same solution strategy that has been successful in the past, even though the solution may no longer be useful. It is commonly seen when students do math problems for homework. Often, several problems in a row require the reapplication of the same solution strategy. Then, without warning, the next problem in the set requires a new strategy. Many students attempt to apply the formerly successful strategy on the new problem and therefore cannot come up with a correct answer.

The thing to remember is that you cannot solve a problem unless you correctly identify what it is to begin with (initial state) and what you want the end result to be (goal state). That may mean looking at the problem from a different angle and representing it in a new way. The correct representation does not guarantee a successful solution, but it certainly puts you on the right track.

A bit more optimistically, the Gestalt psychologists discovered what may be considered the opposite of fixation, namely  insight . Sometimes the solution to a problem just seems to pop into your head. Wolfgang Kohler examined insight by posing many different problems to chimpanzees, principally problems pertaining to their acquisition of out-of-reach food. In one version, a banana was placed outside of a chimpanzee’s cage and a short stick inside the cage. The stick was too short to retrieve the banana, but was long enough to retrieve a longer stick also located outside of the cage. This second stick was long enough to retrieve the banana. After trying, and failing, to reach the banana with the shorter stick, the chimpanzee would try a couple of random-seeming attempts, react with some apparent frustration or anger, then suddenly rush to the longer stick, the correct solution fully realized at this point. This sudden appearance of the solution, observed many times with many different problems, was termed insight by Kohler.

Lest you think it pertains to chimpanzees only, Karl Dunker demonstrated that children also solve problems through insight in the 1930s. More importantly, you have probably experienced insight yourself. Think back to a time when you were trying to solve a difficult problem. After struggling for a while, you gave up. Hours later, the solution just popped into your head, perhaps when you were taking a walk, eating dinner, or lying in bed.

fixation :  when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

functional fixedness :  a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

mental set :  a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

insight :  a sudden realization of a solution to a problem

Solving Problems by Trial and Error

Correctly identifying the problem and your goal for a solution is a good start, but recall the psychologist’s definition of a problem: it includes a set of possible intermediate states. Viewed this way, a problem can be solved satisfactorily only if one can find a path through some of these intermediate states to the goal. Imagine a fairly routine problem, finding a new route to school when your ordinary route is blocked (by road construction, for example). At each intersection, you may turn left, turn right, or go straight. A satisfactory solution to the problem (of getting to school) is a sequence of selections at each intersection that allows you to wind up at school.

If you had all the time in the world to get to school, you might try choosing intermediate states randomly. At one corner you turn left, the next you go straight, then you go left again, then right, then right, then straight. Unfortunately, trial and error will not necessarily get you where you want to go, and even if it does, it is not the fastest way to get there. For example, when a friend of ours was in college, he got lost on the way to a concert and attempted to find the venue by choosing streets to turn onto randomly (this was long before the use of GPS). Amazingly enough, the strategy worked, although he did end up missing two out of the three bands who played that night.

Trial and error is not all bad, however. B.F. Skinner, a prominent behaviorist psychologist, suggested that people often behave randomly in order to see what effect the behavior has on the environment and what subsequent effect this environmental change has on them. This seems particularly true for the very young person. Picture a child filling a household’s fish tank with toilet paper, for example. To a child trying to develop a repertoire of creative problem-solving strategies, an odd and random behavior might be just the ticket. Eventually, the exasperated parent hopes, the child will discover that many of these random behaviors do not successfully solve problems; in fact, in many cases they create problems. Thus, one would expect a decrease in this random behavior as a child matures. You should realize, however, that the opposite extreme is equally counterproductive. If the children become too rigid, never trying something unexpected and new, their problem solving skills can become too limited.

Effective problem solving seems to call for a happy medium that strikes a balance between using well-founded old strategies and trying new ground and territory. The individual who recognizes a situation in which an old problem-solving strategy would work best, and who can also recognize a situation in which a new untested strategy is necessary is halfway to success.

Solving Problems with Algorithms and Heuristics

For many problems there is a possible strategy available that will guarantee a correct solution. For example, think about math problems. Math lessons often consist of step-by-step procedures that can be used to solve the problems. If you apply the strategy without error, you are guaranteed to arrive at the correct solution to the problem. This approach is called using an  algorithm , a term that denotes the step-by-step procedure that guarantees a correct solution. Because algorithms are sometimes available and come with a guarantee, you might think that most people use them frequently. Unfortunately, however, they do not. As the experience of many students who have struggled through math classes can attest, algorithms can be extremely difficult to use, even when the problem solver knows which algorithm is supposed to work in solving the problem. In problems outside of math class, we often do not even know if an algorithm is available. It is probably fair to say, then, that algorithms are rarely used when people try to solve problems.

Because algorithms are so difficult to use, people often pass up the opportunity to guarantee a correct solution in favor of a strategy that is much easier to use and yields a reasonable chance of coming up with a correct solution. These strategies are called  problem solving heuristics . Similar to what you saw in section 6.2 with reasoning heuristics, a problem solving heuristic is a shortcut strategy that people use when trying to solve problems. It usually works pretty well, but does not guarantee a correct solution to the problem. For example, one problem solving heuristic might be “always move toward the goal” (so when trying to get to school when your regular route is blocked, you would always turn in the direction you think the school is). A heuristic that people might use when doing math homework is “use the same solution strategy that you just used for the previous problem.”

By the way, we hope these last two paragraphs feel familiar to you. They seem to parallel a distinction that you recently learned. Indeed, algorithms and problem-solving heuristics are another example of the distinction between Type 1 thinking and Type 2 thinking.

Although it is probably not worth describing a large number of specific heuristics, two observations about heuristics are worth mentioning. First, heuristics can be very general or they can be very specific, pertaining to a particular type of problem only. For example, “always move toward the goal” is a general strategy that you can apply to countless problem situations. On the other hand, “when you are lost without a functioning gps, pick the most expensive car you can see and follow it” is specific to the problem of being lost. Second, all heuristics are not equally useful. One heuristic that many students know is “when in doubt, choose c for a question on a multiple-choice exam.” This is a dreadful strategy because many instructors intentionally randomize the order of answer choices. Another test-taking heuristic, somewhat more useful, is “look for the answer to one question somewhere else on the exam.”

You really should pay attention to the application of heuristics to test taking. Imagine that while reviewing your answers for a multiple-choice exam before turning it in, you come across a question for which you originally thought the answer was c. Upon reflection, you now think that the answer might be b. Should you change the answer to b, or should you stick with your first impression? Most people will apply the heuristic strategy to “stick with your first impression.” What they do not realize, of course, is that this is a very poor strategy (Lilienfeld et al, 2009). Most of the errors on exams come on questions that were answered wrong originally and were not changed (so they remain wrong). There are many fewer errors where we change a correct answer to an incorrect answer. And, of course, sometimes we change an incorrect answer to a correct answer. In fact, research has shown that it is more common to change a wrong answer to a right answer than vice versa (Bruno, 2001).

The belief in this poor test-taking strategy (stick with your first impression) is based on the  confirmation bias   (Nickerson, 1998; Wason, 1960). You first saw the confirmation bias in Module 1, but because it is so important, we will repeat the information here. People have a bias, or tendency, to notice information that confirms what they already believe. Somebody at one time told you to stick with your first impression, so when you look at the results of an exam you have taken, you will tend to notice the cases that are consistent with that belief. That is, you will notice the cases in which you originally had an answer correct and changed it to the wrong answer. You tend not to notice the other two important (and more common) cases, changing an answer from wrong to right, and leaving a wrong answer unchanged.

Because heuristics by definition do not guarantee a correct solution to a problem, mistakes are bound to occur when we employ them. A poor choice of a specific heuristic will lead to an even higher likelihood of making an error.

algorithm :  a step-by-step procedure that guarantees a correct solution to a problem

problem solving heuristic :  a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

confirmation bias :  people’s tendency to notice information that confirms what they already believe

An Effective Problem-Solving Sequence

You may be left with a big question: If algorithms are hard to use and heuristics often don’t work, how am I supposed to solve problems? Robert Sternberg (1996), as part of his theory of what makes people successfully intelligent (Module 8) described a problem-solving sequence that has been shown to work rather well:

• Identify the existence of a problem.  In school, problem identification is often easy; problems that you encounter in math classes, for example, are conveniently labeled as problems for you. Outside of school, however, realizing that you have a problem is a key difficulty that you must get past in order to begin solving it. You must be very sensitive to the symptoms that indicate a problem.
• Define the problem.  Suppose you realize that you have been having many headaches recently. Very likely, you would identify this as a problem. If you define the problem as “headaches,” the solution would probably be to take aspirin or ibuprofen or some other anti-inflammatory medication. If the headaches keep returning, however, you have not really solved the problem—likely because you have mistaken a symptom for the problem itself. Instead, you must find the root cause of the headaches. Stress might be the real problem. For you to successfully solve many problems it may be necessary for you to overcome your fixations and represent the problems differently. One specific strategy that you might find useful is to try to define the problem from someone else’s perspective. How would your parents, spouse, significant other, doctor, etc. define the problem? Somewhere in these different perspectives may lurk the key definition that will allow you to find an easier and permanent solution.
• Formulate strategy.  Now it is time to begin planning exactly how the problem will be solved. Is there an algorithm or heuristic available for you to use? Remember, heuristics by their very nature guarantee that occasionally you will not be able to solve the problem. One point to keep in mind is that you should look for long-range solutions, which are more likely to address the root cause of a problem than short-range solutions.
• Represent and organize information.  Similar to the way that the problem itself can be defined, or represented in multiple ways, information within the problem is open to different interpretations. Suppose you are studying for a big exam. You have chapters from a textbook and from a supplemental reader, along with lecture notes that all need to be studied. How should you (represent and) organize these materials? Should you separate them by type of material (text versus reader versus lecture notes), or should you separate them by topic? To solve problems effectively, you must learn to find the most useful representation and organization of information.
• Allocate resources.  This is perhaps the simplest principle of the problem solving sequence, but it is extremely difficult for many people. First, you must decide whether time, money, skills, effort, goodwill, or some other resource would help to solve the problem Then, you must make the hard choice of deciding which resources to use, realizing that you cannot devote maximum resources to every problem. Very often, the solution to problem is simply to change how resources are allocated (for example, spending more time studying in order to improve grades).
• Monitor and evaluate solutions.  Pay attention to the solution strategy while you are applying it. If it is not working, you may be able to select another strategy. Another fact you should realize about problem solving is that it never does end. Solving one problem frequently brings up new ones. Good monitoring and evaluation of your problem solutions can help you to anticipate and get a jump on solving the inevitable new problems that will arise.

Please note that this as  an  effective problem-solving sequence, not  the  effective problem solving sequence. Just as you can become fixated and end up representing the problem incorrectly or trying an inefficient solution, you can become stuck applying the problem-solving sequence in an inflexible way. Clearly there are problem situations that can be solved without using these skills in this order.

Additionally, many real-world problems may require that you go back and redefine a problem several times as the situation changes (Sternberg et al. 2000). For example, consider the problem with Mary’s daughter one last time. At first, Mary did represent the problem as one of defiance. When her early strategy of pleading and threatening punishment was unsuccessful, Mary began to observe her daughter more carefully. She noticed that, indeed, her daughter’s attention would be drawn by an irresistible distraction or book. Fresh with a re-representation of the problem, she began a new solution strategy. She began to remind her daughter every few minutes to stay on task and remind her that if she is ready before it is time to leave, she may return to the book or other distracting object at that time. Fortunately, this strategy was successful, so Mary did not have to go back and redefine the problem again.

Pick one or two of the problems that you listed when you first started studying this section and try to work out the steps of Sternberg’s problem solving sequence for each one.

a mental representation of a category of things in the world

an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

knowledge about one’s own cognitive processes; thinking about your thinking

individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

Thinking like a scientist in your everyday life for the purpose of drawing correct conclusions. It entails skepticism; an ability to identify biases, distortions, omissions, and assumptions; and excellent deductive and inductive reasoning, and problem solving skills.

a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

an inclination, tendency, leaning, or prejudice

a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

a set of statements in which the beginning statements lead to a conclusion

an argument for which true beginning statements guarantee that the conclusion is true

a type of reasoning in which we make judgments about likelihood from sets of evidence

an inductive argument in which the beginning statements lead to a conclusion that is probably true

fast, automatic, and emotional thinking

slow, effortful, and logical thinking

a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

udging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

noticing, comprehending and forming a mental conception of a problem

when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

a sudden realization of a solution to a problem

a step-by-step procedure that guarantees a correct solution to a problem

The tendency to notice and pay attention to information that confirms your prior beliefs and to ignore information that disconfirms them.

a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

Introduction to Psychology Copyright © 2020 by Ken Gray; Elizabeth Arnott-Hill; and Or'Shaundra Benson is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Chapter 9: Facilitating Complex Thinking

Problem-solving.

Somewhat less open-ended than creative thinking is problem solving , the analysis and solution of tasks or situations that are complex or ambiguous and that pose difficulties or obstacles of some kind (Mayer & Wittrock, 2006). Problem solving is needed, for example, when a physician analyzes a chest X-ray: a photograph of the chest is far from clear and requires skill, experience, and resourcefulness to decide which foggy-looking blobs to ignore, and which to interpret as real physical structures (and therefore real medical concerns). Problem solving is also needed when a grocery store manager has to decide how to improve the sales of a product: should she put it on sale at a lower price, or increase publicity for it, or both? Will these actions actually increase sales enough to pay for their costs?

Example 1: Problem Solving in the Classroom

Problem solving happens in classrooms when teachers present tasks or challenges that are deliberately complex and for which finding a solution is not straightforward or obvious. The responses of students to such problems, as well as the strategies for assisting them, show the key features of problem solving. Consider this example, and students’ responses to it. We have numbered and named the paragraphs to make it easier to comment about them individually:

Scene #1: A problem to be solved

A teacher gave these instructions: “Can you connect all of the dots below using only four straight lines?” She drew the following display on the chalkboard:

The problem itself and the procedure for solving it seemed very clear: simply experiment with different arrangements of four lines. But two volunteers tried doing it at the board, but were unsuccessful. Several others worked at it at their seats, but also without success.

Scene #2: Coaxing students to re-frame the problem

When no one seemed to be getting it, the teacher asked, “Think about how you’ve set up the problem in your mind—about what you believe the problem is about. For instance, have you made any assumptions about how long the lines ought to be? Don’t stay stuck on one approach if it’s not working!”

Scene #3: Alicia abandons a fixed response

After the teacher said this, Alicia indeed continued to think about how she saw the problem. “The lines need to be no longer than the distance across the square,” she said to herself. So she tried several more solutions, but none of them worked either.

The teacher walked by Alicia’s desk and saw what Alicia was doing. She repeated her earlier comment: “Have you assumed anything about how long the lines ought to be?”

Alicia stared at the teacher blankly, but then smiled and said, “Hmm! You didn’t actually say that the lines could be no longer than the matrix! Why not make them longer?” So she experimented again using oversized lines and soon discovered a solution:

Scene #4: Willem’s and Rachel’s alternative strategies

Meanwhile, Willem worked on the problem. As it happened, Willem loved puzzles of all kinds, and had ample experience with them. He had not, however, seen this particular problem. “It must be a trick,” he said to himself, because he knew from experience that problems posed in this way often were not what they first appeared to be. He mused to himself: “Think outside the box, they always tell you. . .” And that was just the hint he needed: he drew lines outside the box by making them longer than the matrix and soon came up with this solution:

When Rachel went to work, she took one look at the problem and knew the answer immediately: she had seen this problem before, though she could not remember where. She had also seen other drawing-related puzzles, and knew that their solution always depended on making the lines longer, shorter, or differently angled than first expected. After staring at the dots briefly, she drew a solution faster than Alicia or even Willem. Her solution looked exactly like Willem’s.

This story illustrates two common features of problem solving: the effect of degree of structure or constraint on problem solving, and the effect of mental obstacles to solving problems. The next sections discuss each of these features, and then looks at common techniques for solving problems.

The effect of constraints: well-structured versus ill-structured problems

Problems vary in how much information they provide for solving a problem, as well as in how many rules or procedures are needed for a solution. A well-structured problem provides much of the information needed and can in principle be solved using relatively few clearly understood rules. Classic examples are the word problems often taught in math lessons or classes: everything you need to know is contained within the stated problem and the solution procedures are relatively clear and precise. An ill-structured problem has the converse qualities: the information is not necessarily within the problem, solution procedures are potentially quite numerous, and a multiple solutions are likely (Voss, 2006). Extreme examples are problems like “How can the world achieve lasting peace?” or “How can teachers insure that students learn?”

By these definitions, the nine-dot problem is relatively well-structured—though not completely. Most of the information needed for a solution is provided in Scene #1: there are nine dots shown and instructions given to draw four lines. But not all necessary information was given: students needed to consider lines that were longer than implied in the original statement of the problem. Students had to “think outside the box,” as Willem said—in this case, literally.

When a problem is well-structured, so are its solution procedures likely to be as well. A well-defined procedure for solving a particular kind of problem is often called an algorithm ; examples are the procedures for multiplying or dividing two numbers or the instructions for using a computer (Leiserson, et al., 2001). Algorithms are only effective when a problem is very well-structured and there is no question about whether the algorithm is an appropriate choice for the problem. In that situation it pretty much guarantees a correct solution. They do not work well, however, with ill-structured problems, where they are ambiguities and questions about how to proceed or even about precisely what the problem is about. In those cases it is more effective to use heuristics , which are general strategies—“rules of thumb,” so to speak—that do not always work, but often do, or that provide at least partial solutions. When beginning research for a term paper, for example, a useful heuristic is to scan the library catalogue for titles that look relevant. There is no guarantee that this strategy will yield the books most needed for the paper, but the strategy works enough of the time to make it worth trying.

In the nine-dot problem, most students began in Scene #1 with a simple algorithm that can be stated like this: “Draw one line, then draw another, and another, and another.” Unfortunately this simple procedure did not produce a solution, so they had to find other strategies for a solution. Three alternatives are described in Scenes #3 (for Alicia) and 4 (for Willem and Rachel). Of these, Willem’s response resembled a heuristic the most: he knew from experience that a good general strategy that often worked for such problems was to suspect a deception or trick in how the problem was originally stated. So he set out to question what the teacher had meant by the word line , and came up with an acceptable solution as a result.

Common obstacles to solving problems

The example also illustrates two common problems that sometimes happen during problem solving. One of these is functional fixedness : a tendency to regard the functions of objects and ideas as fixed (German & Barrett, 2005). Over time, we get so used to one particular purpose for an object that we overlook other uses. We may think of a dictionary, for example, as necessarily something to verify spellings and definitions, but it also can function as a gift, a doorstop, or a footstool. For students working on the nine-dot matrix described in the last section, the notion of “drawing” a line was also initially fixed; they assumed it to be connecting dots but not extending lines beyond the dots. Functional fixedness sometimes is also called response set , the tendency for a person to frame or think about each problem in a series in the same way as the previous problem, even when doing so is not appropriate to later problems. In the example of the nine-dot matrix described above, students often tried one solution after another, but each solution was constrained by a set response not to extend any line beyond the matrix.

Functional fixedness and the response set are obstacles in problem representation , the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely—if indeed the problem can be solved at all. With the nine-dot matrix problem, for example, construing the instruction to draw four lines as meaning “draw four lines entirely within the matrix” means that the problem simply could not be solved. For another, consider this problem: “The number of water lilies on a lake doubles each day. Each water lily covers exactly one square foot. If it takes 100 days for the lilies to cover the lake exactly, how many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is not relevant to the solution, and only serves to distract from the truly crucial information, the fact that the lilies double their coverage each day. (The answer, incidentally, is that the lake is half covered in 99 days; can you think why?)

Strategies to assist problem solving

Just as there are cognitive obstacles to problem solving, there are also general strategies that help the process be successful, regardless of the specific content of a problem (Thagard, 2005). One helpful strategy is problem analysis —identifying the parts of the problem and working on each part separately. Analysis is especially useful when a problem is ill-structured. Consider this problem, for example: “Devise a plan to improve bicycle transportation in the city.” Solving this problem is easier if you identify its parts or component subproblems, such as (1) installing bicycle lanes on busy streets, (2) educating cyclists and motorists to ride safely, (3) fixing potholes on streets used by cyclists, and (4) revising traffic laws that interfere with cycling. Each separate subproblem is more manageable than the original, general problem. The solution of each subproblem contributes the solution of the whole, though of course is not equivalent to a whole solution.

Another helpful strategy is working backward from a final solution to the originally stated problem. This approach is especially helpful when a problem is well-structured but also has elements that are distracting or misleading when approached in a forward, normal direction. The water lily problem described above is a good example: starting with the day when all the lake is covered (Day 100), ask what day would it therefore be half covered (by the terms of the problem, it would have to be the day before, or Day 99). Working backward in this case encourages reframing the extra information in the problem (i. e. the size of each water lily) as merely distracting, not as crucial to a solution.

A third helpful strategy is analogical thinking —using knowledge or experiences with similar features or structures to help solve the problem at hand (Bassok, 2003). In devising a plan to improve bicycling in the city, for example, an analogy of cars with bicycles is helpful in thinking of solutions: improving conditions for both vehicles requires many of the same measures (improving the roadways, educating drivers). Even solving simpler, more basic problems is helped by considering analogies. A first grade student can partially decode unfamiliar printed words by analogy to words he or she has learned already. If the child cannot yet read the word screen , for example, he can note that part of this word looks similar to words he may already know, such as seen or green , and from this observation derive a clue about how to read the word screen . Teachers can assist this process, as you might expect, by suggesting reasonable, helpful analogies for students to consider.

Bassok, J. (2003). Analogical transfer in problem solving. In Davidson, J. & Sternberg, R. (Eds.). The psychology of problem solving. New York: Cambridge University Press.

German, T. & Barrett, H. (2005). Functional fixedness in a technologically sparse culture. Psychological Science, 16 (1), 1–5.

Leiserson, C., Rivest, R., Cormen, T., & Stein, C. (2001). Introduction to algorithms. Cambridge, MA: MIT Press.

Luchins, A. & Luchins, E. (1994). The water-jar experiment and Einstellung effects. Gestalt Theory: An International Interdisciplinary Journal, 16 (2), 101–121.

Mayer, R. & Wittrock, M. (2006). Problem-solving transfer. In D. Berliner & R. Calfee (Eds.), Handbook of Educational Psychology, pp. 47–62. Mahwah, NJ: Erlbaum.

Thagard, R. (2005). Mind: Introduction to Cognitive Science, 2nd edition. Cambridge, MA: MIT Press.

Voss, J. (2006). Toulmin’s model and the solving of ill-structured problems. Argumentation, 19 (3), 321–329.

• Educational Psychology. Authored by : Kelvin Seifert and Rosemary Sutton. Located at : https://open.umn.edu/opentextbooks/BookDetail.aspx?bookId=153 . License : CC BY: Attribution

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

What Is Cognitive Psychology?

The Science of How We Think

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Steven Gans, MD is board-certified in psychiatry and is an active supervisor, teacher, and mentor at Massachusetts General Hospital.

Topics in Cognitive Psychology

• Current Research
• Cognitive Approach in Practice

Careers in Cognitive Psychology

How cognitive psychology differs from other branches of psychology, frequently asked questions.

Cognitive psychology is the study of internal mental processes—all of the workings inside your brain, including perception, thinking, memory, attention, language, problem-solving, and learning. Learning about how people think and process information helps researchers and psychologists understand the human brain and assist people with psychological difficulties.

This article discusses what cognitive psychology is—its history, current trends, practical applications, and career paths.

Findings from cognitive psychology help us understand how people think, including how they acquire and store memories. By knowing more about how these processes work, psychologists can develop new ways of helping people with cognitive problems.

Cognitive psychologists explore a wide variety of topics related to thinking processes. Some of these include: 

• Attention --our ability to process information in the environment while tuning out irrelevant details
• Choice-based behavior --actions driven by a choice among other possibilities
• Decision-making
• Information processing
• Language acquisition --how we learn to read, write, and express ourselves
• Problem-solving
• Speech perception -how we process what others are saying
• Visual perception --how we see the physical world around us

History of Cognitive Psychology

Although it is a relatively young branch of psychology , it has quickly grown to become one of the most popular subfields. Cognitive psychology grew into prominence between the 1950s and 1970s.

Prior to this time, behaviorism was the dominant perspective in psychology. This theory holds that we learn all our behaviors from interacting with our environment. It focuses strictly on observable behavior, not thought and emotion. Then, researchers became more interested in the internal processes that affect behavior instead of just the behavior itself. 

This shift is often referred to as the cognitive revolution in psychology. During this time, a great deal of research on topics including memory, attention, and language acquisition began to emerge. 

In 1967, the psychologist Ulric Neisser introduced the term cognitive psychology, which he defined as the study of the processes behind the perception, transformation, storage, and recovery of information.

Cognitive psychology became more prominent after the 1950s as a result of the cognitive revolution.

Current Research in Cognitive Psychology

The field of cognitive psychology is both broad and diverse. It touches on many aspects of daily life. There are numerous practical applications for this research, such as providing help coping with memory disorders, making better decisions , recovering from brain injury, treating learning disorders, and structuring educational curricula to enhance learning.

Current research on cognitive psychology helps play a role in how professionals approach the treatment of mental illness, traumatic brain injury, and degenerative brain diseases.

Thanks to the work of cognitive psychologists, we can better pinpoint ways to measure human intellectual abilities, develop new strategies to combat memory problems, and decode the workings of the human brain—all of which ultimately have a powerful impact on how we treat cognitive disorders.

The field of cognitive psychology is a rapidly growing area that continues to add to our understanding of the many influences that mental processes have on our health and daily lives.

From understanding how cognitive processes change as a child develops to looking at how the brain transforms sensory inputs into perceptions, cognitive psychology has helped us gain a deeper and richer understanding of the many mental events that contribute to our daily existence and overall well-being.

The Cognitive Approach in Practice

In addition to adding to our understanding of how the human mind works, the field of cognitive psychology has also had an impact on approaches to mental health. Before the 1970s, many mental health treatments were focused more on psychoanalytic , behavioral , and humanistic approaches.

The so-called "cognitive revolution" put a greater emphasis on understanding the way people process information and how thinking patterns might contribute to psychological distress. Thanks to research in this area, new approaches to treatment were developed to help treat depression, anxiety, phobias, and other psychological disorders .

Cognitive behavioral therapy and rational emotive behavior therapy are two methods in which clients and therapists focus on the underlying cognitions, or thoughts, that contribute to psychological distress.

What Is Cognitive Behavioral Therapy?

Cognitive behavioral therapy (CBT) is an approach that helps clients identify irrational beliefs and other cognitive distortions that are in conflict with reality and then aid them in replacing such thoughts with more realistic, healthy beliefs.

If you are experiencing symptoms of a psychological disorder that would benefit from the use of cognitive approaches, you might see a psychologist who has specific training in these cognitive treatment methods.

These professionals frequently go by titles other than cognitive psychologists, such as psychiatrists, clinical psychologists , or counseling psychologists , but many of the strategies they use are rooted in the cognitive tradition.

Many cognitive psychologists specialize in research with universities or government agencies. Others take a clinical focus and work directly with people who are experiencing challenges related to mental processes. They work in hospitals, mental health clinics, and private practices.

Research psychologists in this area often concentrate on a particular topic, such as memory. Others work directly on health concerns related to cognition, such as degenerative brain disorders and brain injuries.

Treatments rooted in cognitive research focus on helping people replace negative thought patterns with more positive, realistic ones. With the help of cognitive psychologists, people are often able to find ways to cope and even overcome such difficulties.

Reasons to Consult a Cognitive Psychologist

• Alzheimer's disease, dementia, or memory loss
• Brain trauma treatment
• Cognitive therapy for a mental health condition
• Interventions for learning disabilities
• Perceptual or sensory issues
• Therapy for a speech or language disorder

Whereas behavioral and some other realms of psychology focus on actions--which are external and observable--cognitive psychology is instead concerned with the thought processes behind the behavior. Cognitive psychologists see the mind as if it were a computer, taking in and processing information, and seek to understand the various factors involved.

A Word From Verywell

Cognitive psychology plays an important role in understanding the processes of memory, attention, and learning. It can also provide insights into cognitive conditions that may affect how people function.

Being diagnosed with a brain or cognitive health problem can be daunting, but it is important to remember that you are not alone. Together with a healthcare provider, you can come up with an effective treatment plan to help address brain health and cognitive problems.

Your treatment may involve consulting with a cognitive psychologist who has a background in the specific area of concern that you are facing, or you may be referred to another mental health professional that has training and experience with your particular condition.

Ulric Neisser is considered the founder of cognitive psychology. He was the first to introduce the term and to define the field of cognitive psychology. His primary interests were in the areas of perception and memory, but he suggested that all aspects of human thought and behavior were relevant to the study of cognition.

A cognitive map refers to a mental representation of an environment. Such maps can be formed through observation as well as through trial and error. These cognitive maps allow people to orient themselves in their environment.

While they share some similarities, there are some important differences between cognitive neuroscience and cognitive psychology. While cognitive psychology focuses on thinking processes, cognitive neuroscience is focused on finding connections between thinking and specific brain activity. Cognitive neuroscience also looks at the underlying biology that influences how information is processed.

Cognitive psychology is a form of experimental psychology. Cognitive psychologists use experimental methods to study the internal mental processes that play a role in behavior.

Sternberg RJ, Sternberg K. Cognitive Psychology . Wadsworth/Cengage Learning. 

Krapfl JE. Behaviorism and society . Behav Anal. 2016;39(1):123-9. doi:10.1007/s40614-016-0063-8

Cutting JE. Ulric Neisser (1928-2012) . Am Psychol . 2012;67(6):492. doi:10.1037/a0029351

Ruggiero GM, Spada MM, Caselli G, Sassaroli S. A historical and theoretical review of cognitive behavioral therapies: from structural self-knowledge to functional processes .  J Ration Emot Cogn Behav Ther . 2018;36(4):378-403. doi:10.1007/s10942-018-0292-8

Parvin P. Ulric Neisser, cognitive psychology pioneer, dies . Emory News Center.

APA Dictionary of Psychology. Cognitive map . American Psychological Association.

Forstmann BU, Wagenmakers EJ, Eichele T, Brown S, Serences JT. Reciprocal relations between cognitive neuroscience and formal cognitive models: opposites attract? . Trends Cogn Sci . 2011;15(6):272-279. doi:10.1016/j.tics.2011.04.002

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Reasoning & Problem Solving

Judith Ellen Fan

Tobias Gerstenberg

Noah Goodman

Hyowon Gweon

Mark Lepper

Jay McClelland

Barbara Tversky

Phd students.

Adani Abutto

Sean Anderson

Catherine Garton

Satchel Grant

Yuxuan (Effie) Li

Andrew (Joo Hun) Nam

Eric Neumann

Kate Petrova

Ben Prystawski

Peter Guandi Zhu

Postdoctoral scholars.

Michael Schwalbe

Research staff.

Kylie Yorke

From Empirical Problem-Solving to Theoretical Problem-Finding Perspectives on the Cognitive Sciences

• Original Paper
• Open access
• Published: 14 October 2024

Cite this article

You have full access to this open access article

• Federico Adolfi   ORCID: orcid.org/0000-0002-4202-5252 1 , 2 ,
• Laura van de Braak 3 &
• Marieke Woensdregt 3 , 4  

299 Accesses

1 Altmetric

Explore all metrics

Meta-theoretical perspectives on the research problems and activities of (cognitive) scientists often emphasize empirical problems and problem-solving as the main aspects that account for scientific progress. While certainly useful to shed light on issues of theory-observation relationships, these conceptual analyses typically begin when empirical problems are already there for researchers to solve. As a result, the role of theoretical problems and problem-finding remain comparatively obscure. How do the scientific problems of Cognitive Science arise, and what do they comprise, empirically and theoretically? Here, we attempt to understand the research activities that lead to adequate explanations through a broader conception of the problems researchers must attend to and how they come about. To this end, we bring theoretical problems and problem-finding out of obscurity to paint a more integrative picture of how these complement empirical problems and problem-solving to advance cognitive science.

Similar content being viewed by others

The Problem-Ladenness of Theory

Introduction: Why Theory? (Mis)Understanding the Context and Rationale

Theoretical Foundations

Avoid common mistakes on your manuscript.

“[...] the quality of the problem that is found is a forerunner of the quality of the solution that is attained, and finding the productive problem may be no less an intellectual achievement than attaining the productive solution [...] A creative solution is the response to a creative problem” (Getzels, 1979 ).

Introduction

How does Cognitive Science make progress? Philosophical analysis of scientific progress has often given a general answer to this question from a problem-solving perspective (e.g., Laudan 1978 ; Popper 1999 ). Cognitive Science has a natural affinity with this view, given its foundational focus on the problem-solving capabilities of cognitive systems (e.g., Newell et al. 1958 ). Likewise, the meta-theory coming from within the cognitive sciences has oftentimes framed the activities of researchers as empirical problem-solving (e.g., Levenstein et al. 2023 ). While certainly useful to shed light on issues such as theory choice and the role of models in mediating theory and observations, these perspectives begin their journeys more or less when empirical problems are already there for researchers to solve. Therefore, the origin of cognitive-scientific problems, and how their theoretical and empirical components interact, typically remains more mysterious.

How do the scientific problems of Cognitive Science get carved out? And what do they comprise, empirically and theoretically? Problem- finding is a comparatively obscure topic within cognitive science itself (Getzels, 1979 ). Similarly, theoretical problems (sometimes called “conceptual”; Laudan, 1988 ) have been given less attention than empirical ones (see Whitt 1988 ). In this paper, we address this imbalance by attempting to understand the research activities that lead to adequate explanations through a broader conception of the problems researchers must attend to and how they come about. To this end, we bring theoretical problems and problem-finding out of obscurity to paint a more integrative picture of how these complement empirical problems and problem-solving within the broader scientific problems and activities of Cognitive Science. We organize our exploration as follows.

In Section “ Categories of Problems and Activities ,” we introduce the main types of problems and activities that are to be contrasted but ultimately integrated. We present the conceptual categories of empirical problems, theoretical problems (§“ Empirical and Theoretical Problems ”), problem-solving, and problem-finding (§“ Problem-Finding and Problem-Solving ”). We highlight what empirical problem-solving lenses underemphasize and preview a more integrative notion that will guide us throughout.

To bring the theoretical side of scientific problems into focus, it is informative to examine paradigmatic types of theoretical problems; we do this in Section “ Plausibility Constraints as Theoretical Problems .” We look at the role of purely theoretical constraints and the theoretical problems that arise in attempts to meet them. Specifically, we describe plausibility constraints as one such problem-generating theoretical device, which we use as a running example throughout.

Theoretical problems can be elusive, and locating problem-finding in the reports and activities of cognitive scientists can be difficult. In Section “ Theoretical Problem-Finding Can Be Elusive ,” we consider the in-principle discoverability of theoretical problems (§“ Discoverability of Theoretical Problems ”), how they might elude us in practice (§“ How Theoretical Problems Elude Us ”), and how this might lead us to construe scientific problems too narrowly (§“ Problems, Too Narrowly Construed ”).

In Section “ Integrating Problem-Solving and Problem-Finding ,” we attempt to rebuild an integrative notion of scientific problems for cognitive science that includes theoretical problems and problem-finding. In particular, we describe a broader view of how scientific problems arise (§“ The Provenance of Cognitive-Scientific Problems ”) and how even phenomena in need of explanation are co-created through theoretical and empirical problem-finding (§“ Phenomena Are Co-Created Through Theoretical (and Empirical) Problem-Finding ”).

To understand the implications of this broader view, in Section “ What We Miss When We Overlook Theoretical Problems ,” we consider what we miss when it is absent from scientific and meta-scientific practice. In particular, we consider some consequences of letting empirical problems lead (§“ When We Let Empirical Problems Lead ”), postponing engagement with theoretical problems (§“ When We Postpone Engaging with Theoretical Problems ”), and the propensity of small-scale, low-complexity empirical domains to become insulated from theoretical problems (§“ The Challenge of Small-Scale Domains ”).

Towards the end, we take a look at the positive side of theoretical problems. In Section “ Theoretical Problems Can Be Productive ,” we describe ways in which they transcend the ordinary use of the word problem, in that they can be productive and carry research forward. This includes the ability of theoretical problems to occasion theory revisions which in turn restructure empirical problems (§“ Theory Revision Driven by Cognitive Scope Violations ”) and their ability to guide the exploration of the boundaries of plausible explanations (§“ Exploring the Boundaries of Plausible Theories ”).

Finally, in Section “ Problem-Finding Without Problem-Solving ,” we briefly draw attention to the fact that, by necessity, problem-finding must often be conducted even without problem-solving. Section “ Outroduction ” closes with a few overarching remarks as we consider what this integrative view means for cognitive science more broadly.

Throughout this journey from empirical problem-solving to theoretical problem-finding perspectives, we will encounter two overarching themes: (1) from a scientific point of view, we can only hope to arrive at adequate explanations if we consider empirical and theoretical problems on equal footing, and (2) from a meta-scientific perspective, we can only account for how scientific problems arise and how adequate explanations are discovered if we consider both empirical and theoretical problem-finding/solving together.

With this road map in place, let us begin.

Categories of Problems and Activities

To begin our exploration, we first draw necessary distinctions between empirical and theoretical problems as understood in the philosophy of science and between problem-solving and problem-finding—a much less explored contrast.

Empirical and Theoretical Problems

The idea of cognitive science as empirical problem-solving can be a powerful organizing thought (e.g., Levenstein et al. 2023 ). It can help us zoom in on the local purposes of theories and models, and how they are used in practice. Yet, the modal reading of this analogy is often through an empiricist lens that has been argued to hold back cognitive science more generally (see Goldrick 2022 ; van Rooij and Baggio 2021 , 2020 ).

Radical empiricist views of science hold that it is primarily the accumulation of rigorously gathered observations and the detection of regularities therein which give rise to and form the bedrock of theories, and that the latter should be evaluated primarily on how precisely they retrodict, Footnote 1 those observations, predict new ones, and lead to better control of systems of interest (e.g., Nosek et al. 2018 ). In other words, on this view, theories emerge from empirical problem-finding/solving activities and are appraised on how successful they are at solving empirical problems,, Footnote 2

Interestingly, it was to counter these empiricist lenses that it was deemed necessary to foreground a distinction between empirical and non-empirical problems (Laudan, 1988 ; Whitt, 1988 and refs. therein). The bipartite account of scientific problem-solving was framed as follows. A puzzling phenomenon requires an explanation and hence poses an empirical problem. A scientist interested in this phenomenon may put forth a theory in an attempt to explain it (i.e., “solve” the empirical problem). In addition to retrodicting observations associated with the phenomenon, the theory might make other predictions. If these are contradicted by subsequent observations, the latter become anomalies posing further empirical problems. However, the theory itself might also conflict with other accepted theories or principles. For instance, a computational cognitive theory might run against accepted principles in the Theory of Computability and Complexity (see Garey and Johnson 1979 ; Reiter and Johnson 2013 ). These clashes represent non-empirical problems (sometimes called conceptual problems) that need to be resolved. From here onward, we will refer to problems of this non-empirical kind as theoretical problems . Footnote 3

The importance of introducing these distinctions was, among other things, that it allowed philosophers to frame the following meta-theoretical observation: it is often the case that a new theory manages to account for so-far-unexplained empirical observations only at the cost of introducing a number of theoretical problems (Laudan, 1988 ). Furthermore, it was necessary to point out that “[...] it is possible that a change from an empirically well-supported theory to a less well-supported one could be progressive, provided that the latter resolved significant conceptual difficulties confronting the former” ( ibid.) .

Even when a certain domain of inquiry is initially construed around an empirical phenomenon, the issues quickly revolve around theoretical problems (Popper, 1999 ). There are fewer ways of accounting for observations while remaining self-consistent and cohering with existing knowledge than without these constraints; therefore, a substantial portion of time and effort is devoted to engagement with these theoretical problems. However, the pragmatic view of science as problem-solving tends to focus disproportionately on empirical problem-solving (e.g., Nosek et al. 2018 ; Yarkoni and Westfall 2017 ). This is despite the overarching goal of cognitive science of accounting for behavioral observations subject to cognitive-theoretic constraints . More generally, resistance to admit theoretical problems and their appraisal into accounts of how scientists arrive at explanations seems to have been common beyond cognitive science. “[T]he usual response when confronted with cases in which theories are being appraised along non-empirical vectors has been to deplore the intrusion of these nonscientific considerations [...]” (Laudan, 1988 ).

Schematic of some of the possible relationships that can exist between successively conjectured theories, pre-existing knowledge, and observations, such that empirical and theoretical problems give rise to scientific problems. Empirical problems (top center) are located between theory and observation, while theoretical problems (bottom center) are located between theory and existing knowledge. Red arrows indicate relationships that play a role in problem-finding , while blue ones are associated with problem-solving . Other relationships between theory and observation that are often neglected by empirical problem-solving accounts include assumption (green arrow) and explanation (golden arrow) of empirical observations. In the process of iteratively refining or comprehensively updating theories to solve problems (center; left to right), one or more of these relationships can change or become unknown (purple arrows). During this adjustment, a substantial reconfiguration of the space of empirical/theoretical problems can occur as certain observations —and, less frequently, some existing knowledge —might go from relevant to irrelevant and vice versa

Problem-Finding and Problem-Solving

“[...] to call attention to the neglect of problem-finding as against problem-solving in cognitive science” (Getzels, 1979 ).

The discussions alluded to thus far, regarding empirical versus theoretical problems, have often been too narrowly framed in that they revolve mainly around the idea of problem- solving . Curiously absent is how problems (let alone theoretical ones) are found in the first place: the process of problem- finding . The tendency to focus on problem-solving at the expense of problem-finding can be gleaned in the very foundations of Cognitive Science (e.g., Newell et al. 1958 ), where the pinnacle of human cognition as an object of study was deemed to be its problem-solving capabilities (see also Getzels 1979 ). Similarly, in research reports, cognitive scientists are more likely to discuss how empirical phenomena (empirical problems) are predicted (solved), less so how empirical or theoretical problems are found or how the latter are dealt with (see also Newell 1973 ). This is striking considering that even (so-called empirical) phenomena can be the outcome of sophisticated, perspectival theoretical processes (Massimi, 2022 ). Footnote 4

To preview a more integrative view, scientific problems arguably arise through the interaction between theoretical and empirical problems (see Fig.  1 ). Theoretical problem-finding is the heterogeneous set of processes through which theoretical devices (e.g., mathematical and computational models, qualitative accounts, conceptual analyses) are explicitly made to confront other existing knowledge (e.g., domain-adjacent theories, computational constraints) in order to remove flaws of various kinds in conjectured theories (Fig.  1 , bottom). This is in contrast to empirical problem-finding , where phenomena of interest are framed as explananda—against the backdrop of theories and theoretical problems—and critical data are sought such that theory can be confronted with observation, for instance, to compare the retro/predictions of candidate theories or to point to deficiencies in established theories (Fig.  1 , top).

The reason theoretical problem-finding is largely absent from our accounts of how cognitive scientists make progress seems to be an overly narrow and compartmentalized conception of scientific progress. In particular, one that centers an impoverished notion of empirical problem- solving : when models retrodict observational/experimental data. As we move forward, we will attempt to rebuild an integrative view and put the problems faced by cognitive scientists back together. One of our main points will be that it is not possible to frame so-called empirical problems in meaningful ways in the absence of relevant theoretical problems. Let us first briefly describe theoretical problem types that will serve as running examples later on.

Plausibility Constraints as Theoretical Problems

“[...] of course, science is about finding out what is actual. But you should care about what is possible because, in the absence of a God’s-eye access to reality, knowing what is possible is an important (dare I say, it is the only) guide to find out what is actual” (Massimi, 2022 ).

In order to make the core issues we introduced above more concrete, we will occasionally delve into illustrative examples. These include hypothetical scenarios and real instances of theories running into specific kinds of theoretical problems. These, we argue, are caused by theoretical plausibility constraints. Two example constraints featured in this paper are tractability (van Rooij, 2008 ; van Rooij et al., 2019 ) and cognitive scope . We briefly explain the rationale behind plausibility constraints before moving on.

Humans, as well as all other natural and artificial cognitive systems, have limited resources available for computation. This limitation imposes a constraint on the set of cognitive capacities that can be plausibly conjectured. That is, plausible theories of cognition cannot (ultimately) put forward computations for which there cannot exist resource-efficient procedures. This, in a nutshell, is the tractability constraint on cognitive theories (for details on how this intuitive notion was shaped and variously formalized, see van Rooij 2008 ; Wareham 1996 ). We cannot apprehend cognitive capacities directly, but sophisticated mathematical machinery exists to make these aspects of our theories intelligible to us. “[V]aluable insights can be derived via complexity-theoretic hardness results which show what cannot be done over a wide range of machines and input sizes” (Wareham, 1996 ). As another example of plausibility constraint, consider computability as a lower bar (Fleck, 2009 ). Uncomputable functions, those for which there cannot exist procedures to compute them (let alone efficient ones), cannot be part of plausible cognitive theories.

Consider next another plausibility constraint: cognitive scope . A theory violates a cognitive scope constraint when it incorporates an assumption that is at odds with the real-world generality of the cognitive capacity studied. The violation of cognitive scope often stems from adopting an assumption that is unnecessary theoretically but crucial empirically (i.e., to “solve” the problem; we will show how this can happen in §“ Theory Revision Driven by Cognitive Scope Violations ”). As a result of this, the local conceptualization and modeling of the capacity underestimates human cognition. In this sense, the (implicit) theory represents an undergeneralization .

These are just examples of some problem-inducing constraints which happen to have broad applicability. Related constraints under the general “plausibility” umbrella are evolvability (Barron et al., 2023 ; Brown, 2014 ; Kaznatcheev, 2019 ; Rich et al., 2020 ), learnability (Angluin, 1992 ), and developability (Abouheif et al., 2014 ; Laland et al., 2015 ), among others (see Blokpoel 2018 , for a similar overview of theoretical constraints on explanations of cognitive capacities). Many other types exist, of various levels of generality and applicability (Adolfi, 2024 ).

Three observations will be useful to bear in mind going forward: (1) constraints such as tractability , computability , and cognitive scope represent a priori explanatory challenges and hence can shape both theoretical and empirical aspects of scientific questions; (2) these constraints can generate theoretical problems when confronted with existing theories and hence prompt a reassessment of what the relevant empirical problems should be; and (3) explanations involving violations of these constraints can be rejected or amended, partially or completely, on purely theoretical grounds. We will elaborate gradually on each of these as we progress through the rest of the sections.

Theoretical Problem-Finding Can Be Elusive

Theoretical problems, as a conceptual category, have been important to understand how researchers arrive at better explanations (see Whitt 1988 , and refs. therein). However, our tradition of research reporting is not always transparent on this, and readers of the cognitive science literature could not be blamed for underestimating the role of theoretical problem-finding. It is possible to attribute the (in)visibility of theoretical problems and problem-finding to various qualitatively different causes. We explore some of them next.

Discoverability of Theoretical Problems

From a meta-theoretical standpoint, not all problems are readily discoverable from just any of the various forms of theory. For a given theoretical problem to be discoverable, theoretical objects must be available that are amenable to scrutiny in problem-type-specific ways. Some kinds of theoretical objects (e.g. verbal statements, varieties of computational models, and mathematical descriptions) will lend themselves to some analyses but not others. For some problems to be uncovered, a prerequisite might be to have computational models (see Guest and Martin 2021 ; van Rooij 2022 ) to perform theoretically guided simulations. Other kinds of problems are only visible through modeling at a more abstract level that enables broadly generalizable analyses. For instance, uncovering the sources of intractability in a cognitive theory requires a formulation at the computational level of analysis (Marr, 1982 ; Varma, 2014 ; van Rooij et al., 2019 ) which is usually not available or easily obtainable from verbal, or even algorithmic, theories (see Adolfi et al. 2022 ; Woensdregt et al. 2021 ). Similarly, discovering (possibly mistaken) philosophical assumptions can be harder to do from formal models alone than from theories that make their conceptual commitments explicit. Quantitative theories afford critiques that qualitative ones do not, and vice versa. Each possible theoretical problem might require a certain “view”—or indeed, a new development—of the theory at the appropriate level of detail, idealization and abstraction. Footnote 5 In the absence of this view, theoretical problems remain out of sight and out of mind.

From a sociology of science perspective, “it is often outsiders who see a problem first” (Popper, 1999 ). Specifically, these problems are often better spotted from the point of view of a theorist who is also a meta-theorist. Since theoretical problems often come from this “outsider” perspective (see Guest, 2024 , for related issues), they might take longer to be assimilated into the mainstream research strands where theory and experiment meet.

How Theoretical Problems Elude Us

Perhaps due to (i) the loose connection that often exists between experimental and theoretical strands in any given research domain, and (ii) a tradition of research reporting centered around empirical data, theoretical problems and problem-finding can easily elude an honest reader of the literature in the cognitive sciences. For instance, it is often the case that the focus of reports is mainly on what an experimental procedure or computational model can do in terms of data generation or fitting and the patterns that can be gleaned therein. That is, they mainly revolve around empirical problem-solving, narrowly construed. Much less common is to focus on how these modeling and analytic devices might stem from having tackled theoretical problems and how these fit within the broader scientific questions.

For a reader, this might have the undesirable effect of giving the appearance that theoretical problems are not at play and that theoretical problem-finding has not taken place. But as a scientific custom, it also has another unintended consequence: it keeps theoretical problems at a safe distance from so-called empirical problems. When this happens, necessary constraints that would otherwise cause theoretical problems might be implicitly and unintentionally assumed to hold. These (often implicit) assumptions are seldom checked (Adolfi et al., 2022 ; van Rooij et al., 2008 ). Concerns about such theoretical constraints are often downgraded to informal discussion of the underlying theory or framework. Often they are relegated to the choice of language or framework to express our theories, a choice that is often justified in practical terms or alluding to technological concerns rather than theoretical ones.

It is tempting to dismiss theoretical problems altogether as they arise on the grounds that they do not make a difference in practice. From a pragmatic point of view, it is possible to cast theoretical principles—in particular, those that would otherwise cause theoretical problems—as “non-falsifiable” or “non-testable,” therefore not within the purview of efforts to solve empirical problems. In certain scenarios, theoretical problems can be understood in this way as unrelated to what is the case in practice. This is possible because it is often the case that even when a theoretical problem is brought to the foreground, it does not change empirical predictions ( for the observations at hand .)

If not dismissing, then postponing can often seem like a reasonable course of action. Using an operationist lens, one could argue for putting off a given theoretical problem until such time as it might be embodied in datasets and empirical tests (e.g., see Yarkoni and Westfall 2017 ). For instance, this rationale is embedded in the research culture of many fields drawing heavily from empirical machine learning frameworks. For any given problem, it materializes only when a “benchmark dataset” is constructed to support model evaluation (see Bender and Koller 2020 ; Birhane et al. 2022 ; Raji et al. 2021 ). Footnote 6

Problems, Too Narrowly Construed

“[...] in real life, many exercises in which model choice relies too heavily on quantitative measures of performance are essentially selecting models based on their ancillary assumptions. It is unclear to me if this solves a scientific problem of interest” (Navarro, 2019 ).

From a pragmatic perspective, it would seem rational to substitute relevant empirical problems for theoretical ones whenever these arise. Of relevance here is how this strategy could contribute to a narrow construal of the scientific problems cognitive scientists face.

This pragmatic facet of research strategizing appears in various forms in many domains. The following kind of appraisal (selected for no particular reason) is not rare and can be easily misinterpreted as shallow empirical problem-solving: “[...] the question of whether [large language models] can inform our theories of human language understanding is first and foremost an empirical question” (Pavlick, 2023 ). There are reasonable interpretations of these kinds of statements that do not necessarily contradict an integrative view of theoretical development and empirical observation. The issue with construing scientific problems narrowly around empirical problem-solving, however, is that one can inadvertently remove (from view) the challenge of finding and solving the theoretical problems that are inextricably linked (i.e., the lower half of the schematic in Fig.  1 ). For instance, on the status of large language models as theoretical devices that might inform questions of human cognition, it might seem sensible to impose a purely behavioral/neural criterion (e.g., Schrimpf et al. 2020 ). That is, from a pragmatic point of view, we might want to substitute the original question with whether an empirical test fails to show a difference between humans and models. If it fails, then models are similar enough that they should be informative. However, there are innumerable ways in which we, as researchers, can be sidetracked by deploying this kind of methodological rule in isolation (see Bowers et al. 2022 , and refs. therein). Models can mimic human behavior and neural patterns through different underlying mechanisms, and only a select few of them are generally of scientific interest (Guest & Martin, 2023 ). A safer methodological rule would also include, for instance, an appraisal of mechanistic explanations of how both human language and large language models work (e.g., Adolfi et al. 2023 ; Oota et al. 2023 ), and how each of these accounts copes with relevant theoretical problems. These may include, for example, considerations on the computational expressivity of the transformer architecture of language models (Strobl et al., 2023 ) as compared to human language capacities.

More generally, radically pragmatic methodological rules for cognitive science have been criticized for their tendency to reframe scientific questions such that they become approachable with bottom-up quasi-mechanical procedures, possibly reflecting misconceptions about how knowledge can plausibly be produced. These include, to give some examples, (a) that cognitive explanations are mainly obtained by the discovery and accumulation of stable experimental effects, emphasizing empirical testing (see van Rooij and Baggio 2021 ; b) that much of cognitive science is an amalgam of automatable tasks (see Adolfi and van Rooij 2023 ; Rich et al. 2021 ; c) that cumulative cognitive science means conducting massive (atheoretical) replication studies (see Devezer and Buzbas 2021 ; d) that scientific exploration can be proceduralized (see Devezer 2023 ; e) that theory appraisal can be reduced to model selection through predictivity rankings (see Bowers et al. 2023 ; Guest and Martin 2023 ); and (f) that implementation-first approaches emphasizing neural data have a claim to primacy over approaches emphasizing functional analysis (see Niv 2021 ; Poeppel and Adolfi 2020 ). These pragmatic strategies appear elsewhere in cognitive science as well, for example, in statistical modeling: “ [...] much of the model selection literature places too much emphasis on the statistical issues of model choice and too little on the scientific questions to which they attach” (Navarro, 2019 ). In other words, there seems to be an ever-present risk that in the pragmatic substitution of empirical questions for the inevitably intertwined empirical-theoretical problems, we end up impoverishing our original scientific questions.

Integrating Problem-Solving and Problem-Finding

“Need problems be found? [...] The world is of course teeming with dilemmas. But the dilemmas do not present themselves automatically as problems capable of [...] even sensible contemplation. They must be posed [...] in fruitful [...] ways if they are to be moved toward solution. The way the problem is posed is the way the dilemma will be resolved ” (Getzels, 1979 ).

We have been arguing that in conceptualizing cognitive science within the frame of problem-solving, we have generally favored a skewed view of scientific problems. Empirical problem-solving is often centered at the expense of theoretical problem-finding due to an overly narrow conception of what scientific problems comprise and what solving them entails. The result is that we lose sight of how empirical and theoretical aspects of scientific problems influence one another. We shall now gradually bring back into focus a more integrative view of scientific problems which deobfuscates how theoretical problem-finding, together with empirical problem-finding, gives rise to scientific problems of interest in cognitive science.

The Provenance of Cognitive-Scientific Problems

“In order to probe this question, ideas that fit current knowledge as well as possible must be formulated” (Barlow, 1972 )

Accounts of how Cognitive Science makes progress usually begin with empirical problems that need solving. These, the story goes, are embodied in problematizing datasets whose patterns need to be accounted for. For instance, a dataset of neural activity recorded while primates are presented with images might in some sense capture the problem of how the brain computes visual representations that are useful to behave appropriately (e.g., Schrimpf et al. 2020 ). But where do these problems come from? That usually seems less clear and of comparatively little importance. Two issues with the empirical problem-solving frame stand out. Firstly, the word empirical (in opposition of theoretical or conceptual) may give an impression of autonomy of empirical problems that these do not possess with respect to theoretical problems (see Fig.  1 ; as theoretical [empirical] problems are dealt with by successive theory variants, empirical [theoretical] problems may revert to unsolved or their status and/or relevance might become unknown). And secondly, the disproportionate focus on problem-solving leaves little room for the issues of problem-finding: how problems arise in the first place. Scientific problems are not given. They need to be searched for, actively created or carved out. We invest in particular kinds of scientific activity in order to do this.

All problems of scientific interest arguably arise due to gaps, flaws, and conflicts in and between our explanations. When we puzzle over, for instance, how it is possible for people to communicate efficiently and resolve misunderstandings (see van Arkel et al. 2020 ; van de Braak et al. 2021 ), it is not because we are awestruck by intrinsically mysterious, unexpected, or extraordinary observations. Human communication is a wholly unsurprising, commonplace thing. Yet, when looked at through the lens of existing, fallible explanations, communication can (rightly) acquire a problematic appearance (see Micklos and Woensdregt 2022 ). This is because our cognitive explanations of how humans do such things as resolve misunderstandings contain large gaps (we go into case studies in sections §“ The Challenge of Small-Scale Domains ” and §“ Theory Revision Driven by Cognitive Scope Violations ”). And indeed researchers invest time in locating and delimiting the source of these theoretical problems (e.g., van de Braak et al. 2021 ; Woensdregt et al. 2021 ). It is through these interlocking cycles of observation and theoretical activity that the capacity for communication is carved out as a scientific problem for cognitive science at all (see van Rooij and Baggio 2021 ). That a problematizing dataset can at some point be construed as embodying the “empirical problem” of misunderstanding resolution is, in this scheme, a much more parochial affair than the broader scientific problem of explaining human communication.

The fundamental point is that problems do not reveal themselves ready for us to solve. We seek them out and shape them, not only “out there” but also “in here,” within our own explanations.

Phenomena Are Co-Created Through Theoretical (and Empirical) Problem-Finding

“Traditionally scientists are said to explain phenomena that they discover in nature. I say that often they create the phenomena which then become the centerpieces of theory” (Hacking, 1983 ).

The quote above highlights a decades-old conceptual flip that emphasized the until-then-neglected role of experiments. Here, we will argue for a similar conceptual flip but with a focus on how theoretical problem-finding contributes to the creation of phenomena qua primary or secondary explananda. This angle on the issues emphasizes the role of “ perspectival modeling rather than experiments in delivering phenomena ” (Massimi, 2022 ). Footnote 7 On the view we are emphasizing here, empirical problems are but one epistemic tool to bring already existing ideas in conflict with each other. It is only in this sense that “they” may be said to provide scientific problems for cognitive scientists. Arguably, researchers actively carve out empirical phenomena by bringing to bear theoretical problems.

Let us get preliminaries out of the way before delving into this further. We adopt a distinction between primary and secondary explananda (Cummins, 2010 ; van Rooij & Baggio, 2021 ). Cognitive capacities (e.g., the ability to communicate, to reason about sensory experiences) are the primary things to explain in Cognitive Science, by definition. Other phenomena, such as experimental effects (e.g., the face inversion effect, the Stroop effect), are certainly of interest but as secondary explananda. That is, cognitive science, except perhaps in contrived scenarios, is not generally interested in, for instance, the experimental face inversion effect except in the context of explaining how face perception—and visual perception more broadly—works in the real world.

Attempts at investigating cognitive capacities, on the one hand, can foreground explanatory flaws in various ways. For instance, this can happen when it proves challenging to explain them while adhering to cognitive-theoretic plausibility constraints (e.g., tractability). Similarly, these flaws can emerge from our efforts to integrate the explanation of cognitive capacities with other cognitive explanations (known as coherence in the philosophy of science; see Douglas 2013 ; Keas 2018 ). Experimental effects, on the other hand, might be the focus of model comparison because they foreground a clash between a priori plausible theories or because they highlight a flaw in an established theory that fails to explain them. An explanation of effects can also be of interest for other (e.g., applied) goals. In any case, problematizing phenomena become such, in no small part, by virtue of providing avenues to foreground theoretical problems. Conversely, bringing theoretical problems to the foreground allows us to clarify what the relevant problematizing datasets (empirical problems, to entertain this terminology) might be. This highlights how the space of empirical and theoretical problems can reconfigure each other as theories are revised (see Fig.  1 ).

To elaborate on this last point, consider that under a fallibilist epistemology (e.g., Deutsch 2012 ), all (so-called empirical) problems, in the sense of phenomena in need of explanation, are apparent problems. As we have seen, this problematic appearance is a function of existing, inevitably fallible explanations that act as lenses for observing and conceptualizing cognitive phenomena. That is, flaws in available explanations might make it so that certain observations acquire a problematic appearance. A problematic appearance is thus always due to a theoretical misconception in the observer. We just need to find it.

The following is a brief case in point (see Adolfi et al. 2022 , for details) to illustrate how theoretical problem-finding and solving can reconfigure the space of phenomena and hence of empirical problems (see Fig.  1 ). In many cognitive domains where segmentation processes are involved (e.g., speech recognition, event processing, action parsing, music perception), researchers have wondered whether certain observed regularities in the environment might be leveraged by cognitive systems to perform efficient computations. The focus on these empirical patterns was motivated by the need to discover constraints on the segmentation subcomputation, otherwise believed to be an intractable task. Several empirical research programs were launched to characterize these regularities and their interactions. However, the efforts around, and interpretation of, these specific empirical phenomena were due to an informal theoretical assumption that had gone unexamined. It involved a possible misconception about the hardness of the segmentation computation and the possible role of such empirical regularities in alleviating it (Adolfi et al., 2022 ). Once this possibly misconceived assumption is removed, the original role for the regularities in existing cognitive explanations can vanish. The relevance of these observations as problematizing datasets can thus be reconsidered, and the space of empirical problems can be reconfigured ( ibid. ).

The ongoing discussion should suggest that phenomena in need of explanation are actively carved out by cognitive scientists when they observe cognitive behavior, or isolate secondary empirical regularities, through the lens of existing explanations and theoretical constraints . Much in the same way that theories and theoretical problems can be “empirical problem”-laden (Levenstein et al., 2023 ), in the sense that they arise from and depend on efforts to explain particular observations, empirical problem-finding is theory-laden. In particular, this lack of automaticity or autonomy of empirical problem-finding highlights the active role of researchers in bringing to bear theoretical problems to carve out phenomena as scientific problems. “[E]ven if scientists have a hypothesis about what model to use for a particular investigation, how do they apply the model to the world? More specifically, what exactly do they apply the model to? [...] Merely stating that they applied the model [...] does not do justice to the time and effort spent ‘preparing’ the ‘world’ so that the model could be applied to it” (Elliott-Graves, 2020 ).

What We Miss When We Overlook Theoretical Problems

A lot can go wrong if we neglect or postpone thinking in terms of theoretical problems. In this section, we explore some of the ways in which we can be misled, get stuck, waste time and resources, or otherwise miss opportunities to improve our knowledge of cognitive systems.

When We Let Empirical Problems Lead

“[...] empirical adequacy is a poor starting point that could have us picking from among the wrong theories in many contexts.” (Bhakthavatsalam & Cartwright, 2017 ).

Failing to account for empirical observations and failing to attend to theoretical problems have different consequences. When we fail to account for data, we are failing to pre/retrodict aspects of the system of interest. Our ability to evaluate our understanding of the cognitive system, however, remains intact. That is, we can still keep track of the state of our theories, their virtues, and flaws. On the other hand, striving to account for more data while ignoring theoretical problems directly distorts the artifacts that mediate our understanding. This is because it is always possible to accommodate observations in innumerable ways. However, most of these accommodations will generate conflicts with existing, possibly well-established knowledge. If these clashes are systematically overlooked, this amounts to giving up our ability to remove errors that make our theories implausible as explanation-generating devices. These theoretical devices hence lose force as thinking and observation tools. This loss is due to the increasing likelihood that statements derived from the theory, including empirical predictions and conjectures about what data is relevant at all, are the consequence of its overlooked flaws. Sacrificing theoretical constraints distorts our reading of empirical phenomena (e.g., cognitive system behavior) Footnote 8 and diminishes our ability to assess the strengths and weaknesses of our explanations.

When We Postpone Engaging with Theoretical Problems

From an empirical problem-solving mindset, it would seem that we can set up the following procedure to arrive at good theories: (1) take a theory or model that does reasonably well at pre/retrodicting as much empirical data as possible, never mind its theoretical merits for now, and then (2) iteratively fix its theoretical gaps via criticism (without sacrificing empirical adequacy or accuracy) until we arrive at a theory which is difficult to improve further while meeting all relevant criteria. This and related commonsense ideas are unlikely to work in practice. The reason is that the process of producing these good-for-now, hard-to-improve theories cannot be proceduralized efficiently at all, let alone as just described. The landscape of possible explanations is provably far too hard to navigate—both from the functional (Rich et al., 2021 ) and the implementational perspective (Adolfi & van Rooij, 2023 )—to expect that adjusting one constraint at a time can be a sure route to good theories. Consider one salient implication. For any given constraint-violating theory, it is not at all clear that a path to better theories exists such that all intermediate theories violate fewer constraints. The main takeaway should be that leaving theoretical problem-finding as an afterthought of empirical research activities will likely get us stuck.

The Challenge of Small-Scale Domains

“...if we only solve simple problems, we may never learn how to think about the complex ones” (Navarro, 2019 ).

The natural phenomena that cognitive scientists try to explain often take place on a large scale. This scale can be expressed in terms of the spatio-temporal extent, diversity, or complexity of the input to the cognitive process of interest, or of the stored knowledge that is used in this process, among others. Empirical studies aiming to capture such processes necessarily simplify, idealize, and abstract away from some of the breadth and complexity of the real-world phenomenon (see Potochnik 2020 ). That is, experiments usually take place on a small, and possibly also low-complexity, scale. The same is often true for computational models which aim to mediate between theory and experiment. This practical simplification, however, can come, often implicitly, at great cost to theory and explanation.

Here, we illustrate the challenges to theory caused by plausibility constraints not being apparent due to small-scale domains. We discuss a case where theory development progressed mainly through small-scale computational models and experiments, and we bring the consequences into focus. We will see how a broad class of computational models and explanations of natural language properties harboured a detrimental theoretical problem. Furthermore, we will see how theoretical problem-finding uncovered it by proving a violation of plausibility constraints, tracing the source to a particular component of the models (for details, see Woensdregt et al. 2021 ), and locating the broader issue in a disproportionate focus on small-scale domains. But first, we give some background on the phenomenon of interest, the embedding cognitive domains, and the computational models therein.

The phenomenon of interest is language and its structural properties, in particular, those properties shared by most or all natural languages. A classic example of such a design feature (Hockett, 1960 ; Pleyer & Zhang, 2022 ; Wacewicz & Żywiczyński, 2015 ) that we find in all human languages is compositionality : that the meaning of a sentence is (most often) made up of the meaning of its parts and the way in which those parts are combined (Martin & Baggio, 2020 ; Partee, 1984 ; Pylkkänen, 2020 ; Woensdregt et al., 2024 ). Given that language is a cultural artifact that lives in and is produced by the minds of humans, researchers have looked for cognitive explanations for these structural features of language. Are there particular (cognitive) constraints or pressures on the way language is used, learned, and passed on over generations that could explain why different languages across the world, from many different language families, share the same structural properties? (Chater & Christiansen, 2010 ; Christiansen & Chater, 2008 ; Kirby, 2017 ; Smith, 2014 , 2018 ; Spike, 2018 ; Tamariz, 2017 ; Tamariz & Kirby, 2016 ). For example, the property of compositionality may be explained as a result of a trade-off between a need for expressivity (wanting to be able to communicate many different meanings) and a need for compressibility (which makes the language learnable and generalizable; Kirby et al. 2015 ; Motamedi et al. 2019 ; Raviv et al. 2019 ). This is just one illustrative example of the kinds of explanations that have been investigated using the class of agent-based models we focus on here.

Agent-based modeling plays a major role in developing these kinds of explanations because these theories involve interactions between different levels of organization (individual vs. population) and different timescales (from conversation to language acquisition, to cultural evolution). Computational models allow researchers to specify their theories (Guest & Martin, 2021 ) and explore the dynamics that ensue (Madsen et al., 2019 ). In the class of agent-based models, we focus on here— iterated Bayesian language learning models—the cultural evolution of language is simulated by having agents in a population communicate with each other, and having new generations of agents enter the population and learn a language by observing the communicative behavior of agents from the previous generation (see Ferdinand, 2024 ; Kirby et al. 2014 ; Woensdregt et al. 2021 , and references therein). This allows researchers to gain insight into the dynamics that would follow from a particular theory, by manipulating various aspects of the computational model and comparing the results of computer simulations under different conditions.

Over the past \(\sim \) 15 years, this computational modeling work has been complemented with experimental research, in which the process of cultural evolution of language is simulated in the lab. In these iterated learning experiments, transmission chains are created by having human participants learn a miniature (i.e., small-scale, low-complexity) artificial language, followed by a communication phase in which they are asked to use the language in pairs, after which a next pair of participants (simulating the next “generation” of learners) is trained on the output of the previous participants, and so on (see Tamariz, 2017 ; Tamariz & Papa 2023 ), for a reviews).

In many papers published in this field, it is shown that under the conditions that the theory carves out as important, the (small-scale, low-complexity) languages that result at the end of the iterated learning chain show a similar property to that of naturally occurring languages that the theory aims to explain (e.g., compositional structure). However, the exact cognitive biases or communication strategies of the human participants are hard to ascertain. Therefore, these experiments are often combined with computational modeling work that directly implements and manipulates the factors of import put forward by the theory. When the simulation results (also small-scale, low-complexity) obtained with such a model show a similar pattern to the results of the behavioral experiments, this is considered corroborative evidence that the theory indeed explains not only the outcome of the small-scale experiment but also the real-world pattern observed in the world’s natural languages on the ecological scale.

However, using computational complexity analyses (§“ Plausibility Constraints as Theoretical Problems ”), Woensdregt et al. ( 2021 ) showed that the learning model at the core of a subset of these computational models Footnote 9 violates a core plausibility constraint: they are formally intractable. That is, this particular class of models cannot in principle be scaled up from the small-scale domain (usually not exceeding lexicon sizes of 4 words and 4 meanings) to the ecological scale (adult native speakers of English know \(\sim \) 25,000–50,000 words; Brysbaert et al. 2016 ). This property is intrinsic to the theories and models (i.e., it cannot be mitigated by better procedures or technologies). The intractability could be traced to the use of Bayesian inference as the model of learning, in which learners infer a language from the communicative behavior they have observed, by considering the entire hypothesis space of logically possible languages and computing the likelihood that each of those languages would have produced the observed data. If the model of language that is used is a lexicon of signal-meaning mappings, the space of logically possible languages grows exponentially as the number of signals and meanings is increased, and this space cannot be searched efficiently (see Woensdregt et al. 2021 , for more details). On a practical level, this intractability finding proves that simulations run with this particular class of models fundamentally cannot go beyond a small scale. Furthermore, the formal results have important theoretical consequences: (i) we cannot take it on faith that the small-scale effects would scale to large, real-world lexicons, and (ii) even if the large-scale effects would exist, the theory as implemented in the computational model would not explain them.

The practical consequence of this intractability was probably intuited to some extent by the researchers implementing these computational models, as several articles mention mathematical tricks or approximation methods to bring down simulation run times. This can be a useful practical aid, but the main insight for our purposes is that it reveals a problem- solving mindset that works against theory and explanation. It treats the issue as an engineering problem, whereas Woensdregt et al. ( 2021 ) showed it is a fundamentally theoretical problem. What was necessary for theoretical progress (in this case) was formal analyses, which, as we will see in the next sections, allow us not just to identify what makes theories implausible but also provide ways of sculpting them into more plausible ones.

Theoretical Problems Can Be Productive

“[...] as an explanation, it has serious problems. Problems are fruitful things [...]” (Marletto, 2021 ).

Not everything that theoretical problems bring is bad news. Theoretical problem-finding can be crucial even to solving ostensibly empirical problems. “[T]here are at least three ways in which a theory may undergo conceptual growth and refinement, and thereby enhance the conceptual resources which it supplies for empirical problem-solving [...] through the fine-tuning of its concepts; through the achievement of greater consilience; and through the appropriation of the conceptual resources of theories in other domains” (Whitt, 1988 ). This is because, as can happen with empirical problem-finding, theoretical problem-finding may allow us to pinpoint where our understanding is lacking and to explore plausible ways to improve it. But for this, we must meet the challenge of cognitive-theoretic constraints head on. Next, let us take a look at how this can bring a theory out of a state of entrenched misconceptions and thus improve our understanding and point the way forward.

Theory Revision Driven by Cognitive Scope Violations

Experimental setups, often embodying small-scale, localized, or low-complexity versions of real-world phenomena, necessarily introduce ancillary assumptions that help make the empirical exercise feasible. The issue is that these assumptions can be taken onboard later, perhaps inadvertently, as theoretical commitments. Since these originate from small-scale, low-complexity problems, they are likely to be problematic for the reasons we mentioned earlier (§“ The Challenge of Small-Scale Domains ”). Upgrading these local problem assumptions to the level of theory usually sidesteps some theoretical constraints at the cost of introducing other theoretical problems. Hence, these will have to be surfaced later on through theoretical problem-finding. A focus on empirical problem-solving thereafter cannot help, as it will select models based on their hidden ancillary assumptions (Navarro, 2019 ). The following case study illustrates these and other issues.

In communication, people often need to resolve misunderstandings or ambiguous messages (Dingemanse et al., 2015 ; Fusaroli et al., 2017 ; Healey et al., 2018 ). In most computational models that describe how conventions are formed in communication, unambiguous explicit feedback is incorporated as a cognitive crutch to assist in reaching mutual understanding. However, in real life, people do not always need, or even have access to, such explicit feedback. Yet, they communicate successfully. Consider, for example, a phone conversation. Here, it is not possible to physically point at any object one wishes to discuss. Nevertheless, in such scenarios, people still manage to communicate about these objects. This is a design feature of language known as displacement ; meaning, we can refer to things not in the here and now (Hockett, 1960 ). From the point of view of explaining communication, the availability and use of feedback as a necessary component is therefore an inappropriate theoretical/modeling assumption.

Having uncovered the inadequacy of this assumption, van de Braak et al. ( 2021 ) conducted computational modeling work to investigate how reaching such mutual understanding could be done without it. Surprisingly, simulations showed that removing the assumption results in models performing at chance level, even when sophisticated reasoning is provided to compensate for the lack of explicit feedback. This resulted in a standoff between the full generality of the phenomenon as conceptualized and the necessary ancillary assumptions for the models to “work” empirically. As the models are (supposed to be) tied to proposed explanations for the phenomenon, this naturally leads to the conclusion that, as they stand, these explanations are insufficient.

This is an example of a cognitive scope violation (defined back in §“ Plausibility Constraints as Theoretical Problems ”). The assumption at the root of this was incorporated into the theory after an unwarranted focus on a specific set of empirical results rather than real-world theoretical problems (as discovered in van de Braak et al. n.d. ). It was included because otherwise the model would not have been able to “solve” the problematizing datasets at hand (the empirical problems). In other words, it is required for the model to “work” as intended in the smaller context of the experimental setup. Real-world cognition does not need the crutch.

There is an unfortunate link between the so-called empirical problems at hand and the theoretical problems at play. An atheoretical ancillary assumption is made with the goal of improving the performance of the model on a given dataset. This is one clear case wherein such an ancillary assumption undermines eventual cognitive explanations. Here, as we have been arguing to be the case more generally, a narrow view of cognitive science as empirical problem-solving initially resulted in impoverishing our theoretical understanding of cognition. Theoretical problem-finding later restored the latent cognitive-theoretic problems facing researchers in this domain and allowed them to assert the status of available explanations and to stand on firmer ground.

This theoretical problem-finding work led the authors to the following conclusions: “This shows that state-of-the-art computational explanations have difficulty explaining how people solve the puzzle of underdetermination, and that doing so will require a fundamental leap forward.” (van de Braak et al., 2021 ). This change to the theory must be fundamental if we are to reach a plausible explanation. The reason is that conjecturing an alternative explanation that does not lean on the same flawed foundation requires a creative leap away from, not merely an amendment of, the previous explanation. Theoretical problem-finding is integral to indicate clear future paths for theoretical research. Naturally, then, this meta-theoretical insight can be and should be allowed to detach from a “solution” to the problem. We return to this shortly before closing.

Exploring the Boundaries of Plausible Theories

The reader may wonder whether theoretical problem-finding extends only as far as pointing out issues with existing theories. We believe its reach is far greater and more forward-looking. To illustrate this point, consider the following case study (see van Rooij et al. 2011 , for full details).

In the field of human communication, explaining how humans communicate successfully at real-world speed is a challenge (Levinson, 1995 ). Van Rooij et al. ( 2011 ) propose a methodology to perform parameterized complexity analyses (Downey & Fellows, 2013 ; Wareham, 1996 ) to identify possible real-world constraints under which a model of communication can be tractable. These analyses characterize the boundary separating plausible from implausible theories under the constraint of tractability. After establishing intractability results for an unconstrained model, the authors state the following: “Importantly, our analyses do not stop at the intractability results [...]. On the contrary, we view such results as merely the fruitful starting point of rigorous analyses of the sources of complexity in human communication.” (van Rooij et al., 2011 ). They then go on to perform such analyses, which led to identifying a set of parameter restrictions which, if appropriate to characterize real-world conditions, would satisfy plausibly the tractability constraint on the theory. These parameter restrictions can be translated to real-world situational constraints on the phenomenon that is being modeled. Hence, a natural next step is to check, empirically (i.e., via observation and experiment), whether these restrictions hold and if they fulfill the expected roles. For instance, these formal results characterizing what is in principle possible can inform cognitive neuroscience studies investigating whether and how humans exploit these restrictions. Importantly, without the findings from these formal analyses, we would not know where to look.

This brief example illustrates how the integration of theoretical problem-finding into our research practices can inform future theory development for both theoretical and empirical research. The boundaries discovered in this way can be useful in further theoretical research, informing further steps for the sculpting of theory (Blokpoel, 2018 ; van Rooij & Blokpoel, 2020 ). They can also be used in empirical research, as they help determine which experiments might be theoretically meaningful.

Problem-Finding Without Problem-Solving

“I do not offer answers to these questions, but hope to highlight the reasons why psychological researchers cannot avoid asking them” (Navarro, 2019 )

Finally, let us explore whether it is sensible to expect a “problematizing dataset” whenever theoretical problems are raised. This parallels the question whether problem-finding without problem-solving is desirable and, in particular, whether theoretical problem-finding in the absence of empirical problem-solving is possible and necessary.

In some cases, seeking a problematizing set of observations may be a sensible follow-up (i.e., not an immediate requirement) to theoretical problem-finding, but we argue it is not a reasonable expectation in general. Gathering such a problematizing dataset can be either (i) too costly compared to theoretical work Footnote 10 ; (ii) practically infeasible in certain cases (either in the near future or in general); (iii) too hard because it requires separating relevant from irrelevant aspects of the problem—a task which cannot be efficiently proceduralized (Kwisthout, 2012 ); or (iv) simply impossible. That is, even if we could have a problematizing dataset in principle, which is by no means obvious in any given case, it would not seem sensible to immediately expect one.

First, the empirical research necessary to generate such a dataset may be too costly in terms of time or resources. Taking tractability as an example: building a dataset of real-world complexity in all relevant dimensions to assess whether a theory scales beyond toy domains is not guaranteed to be possible. For instance, when it comes to cognitive processes that take place over a long time scale, such as learning, development, or even (cultural) evolution, datasets of ecological scale are likely infeasible to gather through observational or experimental work (either in the near future or at all). Second, interventions of interest on processes such as cognitive development or evolution are in most cases unethical. In such cases, research often takes the form of comparatively small-scale, low-complexity experiments that rely on non-trivial assumptions, such as assuming continuity between the cognition of modern-day human participants and the cognition of our hominin ancestors (such as in the iterated learning experiments investigating language evolution discussed in Section §“ The Challenge of Small-Scale Domains ”) (Woensdregt et al., in press ). Furthermore, such small-scale experiments require being combined with a tractable computational model (and thus tractability analyses; §“ Plausibility Constraints as Theoretical Problems ”) in order to link between the low-complexity data and the ecological-scale implications of the theory (see §“ The Challenge of Small-Scale Domains ”). Third, building a problematizing dataset can be intrinsically hard because it requires a subset of relevant dimensions of the empirical problem to be carved out among all those that could in principle be relevant (Kwisthout, 2012 ).

Therefore, a reframing of theoretical problems in terms of problematizing datasets cannot and should not be expected to follow directly from theoretical problem-finding exercises. To conclude, theoretical problem-finding without problem-solving is possible and necessary.

Outroduction

We have come a long way from an empirical problem-solving frame for Cognitive Science to one that integrates theoretical problem-finding. This journey casts doubts on the idea that cognitive capacities are somehow directly intelligible to cognitive scientists through (solving) empirical problems, narrowly construed. As cognitive scientists and meta-scientists, we can instead redirect our gaze towards the possibility that cognitive science involves actively carving out (theoretically problematic) empirical phenomena and constructing cognitive theories that are intelligible to us. Here, we have begun to bring theoretical problem-finding out of obscurity as a core research activity towards such purposes. Cognitive Science needs (theoretical) problem-finding as much as (empirical) problem-solving.

Availability of Data and Material

Not applicable.

Code Availability

Retrodiction sometimes called postdiction , refers to the accounting of data gathered in conditions already observed prior to the relevant theoretical development. This is in contrast to prediction , where novel data is accounted for.

Note here, in this narrow sense of solving the lack of reference to criteria for when observations could be considered explained .

A more fine-grained distinction can be drawn between internal and external non-empirical problems. Internal problems involve inconsistencies or contradictions within a given theory. External problems involve incompatibility with independent theories or principles. (For illustrative purposes, we focus on this latter type throughout.)

Indeed, in our view, the distinction between empirical and theoretical problems can itself be misleading if taken at face value (we illustrate in section §“ Integrating Problem-Solving and Problem-Finding ”).

This new theoretical development is often taken up by problem finders themselves.

We address the question of whether it is sensible to require a “problematizing dataset” for every theoretical problem in §“ Problem-Finding Without Problem-Solving ”.

These lenses are all correct, or truthful, as far as we are concerned. Our purpose here is not to provide the most veridical frame (whatever that may be) but to restore a lens that we believe is lacking or whose existence has been negated by misconceptions. Hence, although we focus here on the theoretical problem-finding aspect, our overarching hope is to see a diversity of lenses restored.

See van Rooij et al. ( 2023 ) for a related discussion involving machine learning artifacts as cognitive models.

Specifically, this is the case for iterated Bayesian language learning models that use signal-meaning mappings (i.e., a lexicon) as their model of language.

Note we often confuse the cost of research activities with the scientific value of their possible outcomes.

Abouheif, E., Favé, M.-J., Ibarrarán-Viniegra, A. S., Lesoway, M. P., Rafiqi, A. M., & Rajakumar, R. (2014). Eco-Evo-Devo: The time has come. In C. R. Landry & N. Aubin-Horth (Eds.), Ecological genomics: ecology and the evolution of genes and genomes (pp. 107–125). https://doi.org/10.1007/978-94-007-7347-9_6

Adolfi, F., (2024). Computational meta-theory in cognitive science: A theoretical computer science framework (PhD thesis). University of Bristol.

Adolfi, F., Bowers, J. S., & Poeppel, D. (2023). Successes and critical failures of neural networks in capturing human-like speech recognition. Neural Networks, 162 , 199–211.

Article   PubMed   Google Scholar  

Adolfi, F., & van Rooij, I. (2023). Resource demands of an implementationist approach to cognition. In Proceedings of the 21st international conference on cognitive modeling .

Adolfi, F., Wareham, T., & van Rooij, I. (2022). A computational complexity perspective on segmentation as a cognitive subcomputation. Topics in Cognitive Science, 19 .

Angluin, D. (1992). Computational learning theory: Survey and selected bibliography. In Proceedings of the twentyfourth annual ACM symposium on theory of computing (pp. 351–369). New York, NY, USA: Association for Computing Machinery.

Barlow, H. B. (1972). Single units and sensation: A neuron doctrine for perceptual psychology? Perception, 1 (4), 371–394. https://doi.org/10.1068/p010371

Barron, A. B., Halina, M., & Klein, C. (2023). Transitions in cognitive evolution. Proceedings of the Royal Society B: Biological Sciences, 290 (2002), 20230671. https://doi.org/10.1098/rspb.2023.0671

Article   Google Scholar  

Bender, E. M., & Koller, A. (2020). Climbing towards NLU: On meaning, form, and understanding in the age of data. In Proceedings of the 58th annual meeting of the association for computational linguistics (pp. 5185–5198). Online: Association for Computational Linguistics.

Bhakthavatsalam, S., & Cartwright, N. (2017). What’s so special about empirical adequacy? European Journal for Philosophy of Science , 445–465.

Birhane, A., Kalluri, P., Card, D., Agnew, W., Dotan, R., & Bao, M. (2022). The values encoded in machine learning research. In Proceedings of the 2022 ACM conference on fairness, accountability, and transparency (pp. 173–184). New York, USA: Association for Computing Machinery.

Blokpoel, M. (2018). Sculpting computational-level models. Topics in Cognitive Science , 641–648.

Bowers, J. S., Malhotra, G., Adolfi, F. G., Dujmovic, M., Montero, M. L., Biscione, V., . . . Heaton, R. F. (2023). On the importance of severely testing deep learning models of cognition . PsyArXiv.

Bowers, J. S., Malhotra, G., Dujmovic, M., Montero, M. L., Tsvetkov, C., Biscione, V., . . . Blything, R. (2022). Deep problems with neural network models of human vision. Behavioral and Brain Sciences , 1–74.

Brown, R. L. (2014). What evolvability really is. The British Journal for the Philosophy of Science, 65 (3), 549–572. https://doi.org/10.1093/bjps/axt014

Brysbaert, M., Stevens, M., Mandera, P., & Keuleers, E. (2016). How many words do we know? Practical estimates of vocabulary size dependent on word definition, the degree of language input and the participant’s age. Frontiers in Psychology, 7 ,. https://doi.org/10.3389/fpsyg.2016.01116

Chater, N., & Christiansen, M. H. (2010). Language evolution as cultural evolution: How language is shaped by the brain. WIREs Cognitive Science, 1 (5), 623–628. https://doi.org/10.1002/wcs.85

Christiansen, M. H., & Chater, N. (2008). Language as shaped by the brain. Behavioral and Brain Sciences, 31 (5), 489–509. https://doi.org/10.1017/S0140525X08004998

Cummins, R. (2010). The world in the head . New York: Oxford Univ. Press.

Book   Google Scholar  

Deutsch, D. (2012). The beginning of infinity: Explanations that transform the world . London: Penguin.

Google Scholar  

Devezer, B. (2023). There are no shortcuts to theory . MetaArXiv.

Devezer, B., & Buzbas, E. (2021). Minimum viable experiment to replicate. preprint.

Dingemanse, M., Roberts, S. G., Baranova, J., Blythe, J., Drew, P., Floyd, S., & Enfield, N. J. (2015). Universal principles in the repair of communication problems. PLOS ONE, 10 (9), e0136100. https://doi.org/10.1371/journal.pone.0136100

Douglas, H. (2013). The value of cognitive values. Philosophy of Science , 796–806.

Downey, R. G., & Fellows, M. R. (2013). Fundamentals of parameterized complexity . London: Springer.

Elliott-Graves, A. (2020). What is a target system? Biology & Philosophy, 28 .

Ferdinand, V. (2024). The Bayesian iterated learning model. Oxford Handbook of Approaches to Language Evolution, edited by Limor Raviv and Cedric Boeckx. Oxford

Fleck, M. (2009). Theory of Computation .

Fusaroli, R., Tylén, K., Garly, K., Steensig, J., Christiansen, M. H., & Dingemanse, M. (2017). Measures and mechanisms of common ground: Backchannels, conversational repair, and interactive alignment in free and task-oriented social interactions. In The 39th annual conference of the cognitive science society (pp. 2055–5060). Cognitive Science.

Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of NP-completeness . New York: W. H. Freeman.

Getzels, J. W. (1979). Problem finding: A theoretical note. Cognitive Science , 167–172.

Goldrick, M. (2022). An impoverished epistemology holds back cognitive science research. Cognitive Science .

Guest, O. (2024). What makes a good theory, and how do we make a theory good? Computational Brain & Behavior . https://doi.org/10.1007/s42113-023-00193-2

Guest, O., & Martin, A. E. (2021). How computational modeling can force theory building in psychological science. Perspectives on Psychological Science , 789–802.

Guest, O., & Martin, A. E. (2023). On logical inference over brains, behaviour, and artificial neural networks. Computational Brain & Behavior .

Hacking, I. (1983). Representing and intervening: Introductory topics in the philosophy of natural science . Cambridge; New York: Cambridge University Press.

Healey, P. G. T., de Ruiter, J. P., & Mills, G. J. (2018). Editors’ introduction: Miscommunication. Topics in Cognitive Science, 10 (2), 264–278. https://doi.org/10.1111/tops.12340

Hockett, C. F. (1960). The origin of speech. Scientific American, 11 .

Kaznatcheev, A. (2019). Computational complexity as an ultimate constraint on evolution. genetics, 245–265.

Keas, M. N. (2018). Systematizing the theoretical virtues. Synthese , 2761–2793.

Kirby, S. (2017). Culture and biology in the origins of linguistic structure. Psychonomic Bulletin and Review, 24 (1), 118–137. https://doi.org/10.3758/s13423-016-1166-7

Kirby, S., Griffiths, T., & Smith, K. (2014). Iterated learning and the evolution of language. Current Opinion in Neurobiology, 28 , 108–114. https://doi.org/10.1016/j.conb.2014.07.014

Kirby, S., Tamariz, M., Cornish, H., & Smith, K. (2015). Compression and communication in the cultural evolution of linguistic structure. Cognition, 141 , 87–102. https://doi.org/10.1016/j.cognition.2015.03.016

Kwisthout, J. (2012). Relevancy in problem solving: A computational framework. The Journal of Problem Solving .

Laland, K. N., Uller, T., Feldman, M. W., Sterelny, K., Müller, G. B., Moczek, A., & Odling-Smee, J. (2015). The extended evolutionary synthesis: Its structure, assumptions and predictions. Proceedings of the Royal Society B: Biological Sciences, 282 (1813), 20151019. https://doi.org/10.1098/rspb.2015.1019

Laudan, L. (1978). Progress and its problems: Towards a theory of scientific growth (1st paperback print) . Berkeley, Calif.: Univ. of Calif. Press.

Laudan, L. (1988). Conceptual problems re-visited. Studies in History and Philosophy of Science Part A , 531–534.

Levenstein, D., Alvarez, V. A., Amarasingham, A., Azab, H., Chen, Z. S., Gerkin, R. C., . . . Redish, A. D. (2023). On the role of theory and modeling in neuroscience. Journal of Neuroscience , 1074–1088.

Levenstein, D., De Santo, A., Heijnen, S., Narayan, M., Maatman, F. O., Rawski, J., & Wright, C. (2023). The problem-ladenness of theory. https://doi.org/10.31234/osf.io/q6n58

Levinson, S. C. (1995). Interactional biases in human thinking. In E. N. Goody (Ed.), Social intelligence and interaction: Expressions and implications of the social bias in human intelligence (pp. 221–260). Cambridge: Cambridge University Press.

Chapter   Google Scholar  

Madsen, J. K., Bailey, R., Carrella, E., & Koralus, P. (2019). Analytic versus computational cognitive models: AgentBased modeling as a tool in cognitive sciences. Current Directions in Psychological Science, 28 (3), 299–305. https://doi.org/10.1177/0963721419834547

Marletto, C. (2021). The science of can and can’t: A physicist’s journey through the land of counterfactuals . Allen Lane.

Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information . Cambridge, Mass: MIT Press.

Martin, A. E., & Baggio, G. (2020). Modelling meaning composition from formalism to mechanism. Philosophical Transactions of the Royal Society B: Biological Sciences, 375 (20190298). https://doi.org/10.1098/rstb.2019.0298

Massimi, M. (2022). Perspectival realism . New York: Oxford University Press.

Micklos, A., & Woensdregt, M. (2022). Cognitive and interactive mechanisms for mutual understanding in conversation. PsyArXiv.

Motamedi, Y., Schouwstra, M., Smith, K., Culbertson, J., & Kirby, S. (2019). Evolving artificial sign languages in the lab: From improvised gesture to systematic sign. Cognition, 192 , 103964. https://doi.org/10.1016/j.cognition.2019.05.001

Navarro, D. J. (2019). Between the devil and the deep blue sea: Tensions between scientific judgement and statistical model selection. Computational Brain & Behavior , 28–34.

Newell, A. (1973). You can’t play 20 questions with nature and win: projective comments on the papers of this symposium. In Visual information processing (pp. 283–308). https://doi.org/10.1016/B978-0-12-170150-5.50012-3

Newell, A., Shaw, J. C., & Simon, H. A. (1958). Elements of a theory of human problem solving. Psychological Review , 151–166.

Niv, Y. (2021). The primacy of behavioral research for understanding the brain. Behavioral Neuroscience , 601–609.

Nosek, B. A., Ebersole, C. R., DeHaven, A. C., & Mellor, D. T. (2018). The preregistration revolution. Proceedings of the National Academy of Sciences, 115 (11), 2600–2606. https://doi.org/10.1073/pnas.1708274114

Oota, S. R., Çelik, E., Deniz, F., & Toneva, M. (2023). Speech language models lack important brain-relevant semantics. arXiv: 2311.04664 [cs, eess, q-bio]

Partee, B. (1984). Compositionality. In F. Landman & F. Veltman (Eds.), Varieties of formal semantics (pp. 281–311). Dordrecht: Foris.

Pavlick, E. (2023). Symbols and grounding in large language models (p. 20220041). Mathematical, Physical and Engineering Sciences: Philosophical Transactions of the Royal Society A.

Pleyer, M., & Zhang, E. Q. (2022). Re-evaluation Hockett’s design features from a cognitive and neuroscience perspective: The case of displacement.

Poeppel, D., & Adolfi, F. (2020). Against the epistemological primacy of the hardware: The brain from inside out, turned upside down. eNeuro , ENEURO.0215–20.2020.

Popper, K. R. (1999). All life is problem solving . London, New York: Routledge.

Potochnik, A. (2020). Idealization and the aims of science . Chicago, IL: University of Chicago Press.

Pylkkänen, L. (2020). Neural basis of basic composition: What we have learned from the red–boat studies and their extensions. Philosophical Transactions of the Royal Society B: Biological Sciences, 375 (20190299). https://doi.org/10.1098/rstb.2019.0299

Raji, I. D., Bender, E. M., Paullada, A., Denton, E., & Hanna, A. (2021). AI and the everything in the whole wide world benchmark. arXiv. arXiv: 2111.15366 [cs]

Raviv, L., Meyer, A., & Lev-Ari, S. (2019). Compositional structure can emerge without generational transmission. Cognition, 182 , 151–164. https://doi.org/10.1016/j.cognition.2018.09.010

Reiter, E. E., & Johnson, C. M. (2013). Limits of computation: An introduction to the undecidable and the intractable . Boca Raton, FL: CRC Press, Taylor & Francis Group.

Rich, P., Blokpoel, M., de Haan, R., & van Rooij, I. (2020). How intractability spans the cognitive and evolutionary levels of explanation. Topics in Cognitive Science, 12 (4), 1382–1402. https://doi.org/10.1111/tops.12506

Rich, P., de Haan, R., Wareham, T., & van Rooij, I. (2021). How hard is cognitive science? Proceedings of the Annual Meeting of the Cognitive Science Society .

Schrimpf, M., Kubilius, J., Lee, M. J., Murty, N. A. R., Ajemian, R., & DiCarlo, J. J. (2020). Integrative benchmarking to advance neurally mechanistic models of human intelligence. Neuron, 108 (3), 413–423. https://doi.org/10.1016/j.neuron.2020.07.040

Smith, A. D. M. (2014). Models of language evolution and change. Wiley Interdisciplinary Reviews: Cognitive Science, 5 (3), 281–293. https://doi.org/10.1002/wcs.1285

Smith, K. (2018). How culture and biology interact to shape language and the language faculty. Topics in Cognitive Science, 0 (0). https://doi.org/10.1111/tops.12377

Spike, M. (2018). The evolution of linguistic rules. Biology and Philosophy, 32 (6), 1–18. https://doi.org/10.1007/s10539-018-9610-x

Strobl, L., Merrill, W., Weiss, G., Chiang, D., & Angluin, D. (2023). Transformers as recognizers of formal languages: A survey on expressivity. arXiv:2311.00208 . https://doi.org/10.48550/arXiv.2311.00208

Tamariz, M. (2017). Experimental studies on the cultural evolution of language. Annual Review of Linguistics, 3 (1), 389–407. https://doi.org/10.1146/annurev-linguistics-011516-033807

Tamariz, M., & Kirby, S. (2016). The cultural evolution of language. Current Opinion in Psychology, 8 , 37–43. https://doi.org/10.1016/j.copsyc.2015.09.003

Tamariz, M., & Papa, A. (2023). Iterated learning experiments. https://doi.org/10.31234/osf.io/bcp69 . To appear in: Oxford Handbook of Approaches to Language Evolution, edited by Limor Raviv and Cedric Boeckx. Oxford University Press.

van Arkel, J., Woensdregt, M., Dingemanse, M., & Blokpoel, M. (2020). A simple repair mechanism can alleviate computational demands of pragmatic reasoning: Simulations and complexity analysis. In Proceedings of the 24th conference on computational natural language learning (pp. 177–194). Online: Association for Computational Linguistics

van de Braak, L. D., Dingemanse, M., Toni, I., van Rooij, I., & Blokpoel, M. (2021). Computational challenges in explaining communication: How deep the rabbit hole goes. Proceedings of the Annual Meeting of the Cognitive Science Society, 43 (43).

van de Braak, L. D., Dingemanse, M., Toni, I., van Rooij, I., & Blokpoel, M. (n.d.). Understanding misunderstanding: How quick-fix solutions undermine explanation. Unpublished, working title.

van Rooij, I. (2008). The tractable cognition thesis. Cognitive Science , 939–984.

van Rooij, I. (2022). Psychological models and their distractors. Nature Reviews Psychology , 127–128.

van Rooij, I., & Baggio, G. (2020). Theory development requires an epistemological sea change. Psychological Inquiry, 31 (4), 321–325. https://doi.org/10.1080/1047840X.2020.1853477

van Rooij, I., & Baggio, G. (2021). Theory before the test: How to build high-verisimilitude explanatory theories in psychological science. Perspectives on Psychological Science , 682–697.

van Rooij, I., & Blokpoel, M. (2020). Formalizing verbal theories. Social Psychology, 51 (5), 285–298. https://doi.org/10.1027/1864-9335/a000428

van Rooij, I., Blokpoel, M., Kwisthout, J., & Wareham, T. (2019). Cognition and intractability: A guide to classical and parameterized complexity analysis . Cambridge University Press.

van Rooij, I., Evans, P., Müller, M., Gedge, J., & Wareham, T. (2008). Identifying sources of intractability in cognitive models: An illustration using analogical structure mapping. In Proceedings of the annual meeting of the cognitive science society .

van Rooij, I., Guest, O., Adolfi, F., de Haan, R., Kolokolova, A., & Rich, P. (2023). Reclaiming AI as a theoretical tool for cognitive science.

van Rooij, I., Kwisthout, J., Blokpoel, M., Szymanik, J., Wareham, T., & Toni, I. (2011). Intentional communication: Computationally easy or difficult? Frontiers in Human Neuroscience, 5 (52), 1–18. https://doi.org/10.3389/fnhum.2011.00052

Varma, S. (2014). The subjective meaning of cognitive architecture: A Marrian analysis. Frontiers in Psychology .

Wacewicz, S., & Żywiczyński, P. (2015). Language evolution: Why Hockett’s design features are a non-starter. Biosemiotics, 8 (1), 29–46. https://doi.org/10.1007/s12304-014-9203-2

Wareham, H. T. (1996). The role of parameterized computational complexity theory in cognitive modeling. AAAI-96 Workshop Working Notes: Computational Cognitive Modeling: Source of the Power.

Whitt, L. A. (1988). Conceptual dimensions of theory appraisal. Studies in History and Philosophy of Science Part A , 517–529.

Woensdregt, M., Blokpoel, M., Van Rooij, I., & Martin, A. E. (2024). Challenges for a computational explanation of flexible linguistic inference. In 22nd International Conference on Cognitive Modeling . https://doi.org/10.31234/osf.io/e8cmr

Woensdregt, M., Fusaroli, R., Rich, P., Modrák, M., Kolokolova, A., Wright, C., & Warlaumont, A. S. (in press). Lessons for theory from scientific domains where evidence is sparse or indirect. Computational Brain & Behavior .

Woensdregt, M., Spike, M., de Haan, R., Wareham, T., van Rooij, I., & Blokpoel, M. (2021). Why is scaling up models of language evolution hard? Proceedings of the Annual Meeting of the Cognitive Science Society, 43 (43).

Yarkoni, T., & Westfall, J. (2017). Choosing prediction over explanation in psychology: Lessons from machine learning. Perspectives on Psychological Science, 12 (6), 1100–1122. https://doi.org/10.1177/1745691617693393

Download references

Acknowledgements

We thank Iris van Rooij for extensive discussions that have inspired and shaped, directly or indirectly, the ideas presented here. We thank the organizers of the Lorentz Workshop “What makes a good theory? Interdisciplinary perspectives” (20–24 June 2022)—Iris van Rooij, Berna Devezer, Joshua Skewes, Sashank Varma, and Todd Wareham—for creating a space where these ideas could be discussed, not to force consensus, but to make a diversity of views comprehensible. We thank participants Aniello De Santo, Olivia Guest, Daniel Levenstein, Manjari Narayan, and Jon Rawski for attending and/or commenting on the session organized by FA and sharing their feedback. We are grateful to Olivia Guest for providing comments on the manuscript. We have benefited greatly from comments by the reviewers and editor; we are especially thankful to Berna Devezer for thoughtful and comprehensive feedback. FA thanks David Poeppel and Jeff Bowers for support and discussions on the nature of various scientific problems in the cognitive and brain sciences. LvdB thanks Mark Blokpoel and Iris van Rooij for invaluable discussions regarding the value of problem-finding. MW and FA thank Matthew Spike for discussions on various types of plausibility constraints.

Open Access funding enabled and organized by Projekt DEAL. MW was supported by the Dutch Research Council (NWO) under Gravitation Grant 024.001.006 to the Language in Interaction Consortium (postdoc position within Big Question 5). LvdB is supported by a Donders Centre for Cognition (DCC) PhD grant awarded to Mark Blokpoel, Mark Dingemanse, Ivan Toni, and Iris van Rooij. FA is supported by the Ernst-Strüngmann Institute for Neuroscience in Coop. with Max-Planck Society.

Author information

Authors and affiliations.

Ernst Strüngmann Institute for Neuroscience in Cooperation with Max-Planck Society, Frankfurt, Germany

Federico Adolfi

School of Psychological Science, University of Bristol, Bristol, UK

Donders Institute for Brain, Cognition, and Behaviour, Radboud University, Nijmegen, The Netherlands

Laura van de Braak & Marieke Woensdregt

Language and Computation in Neural Systems, Max Planck Institute for Psycholinguistics, Nijmegen, The Netherlands

Marieke Woensdregt

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed to and approved the final manuscript.

Corresponding author

Correspondence to Federico Adolfi .

Ethics declarations

Conflict of interest.

The authors declare no competing interests.

Ethics Approval

Consent to participate.

Not applicable

Consent for Publication

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Adolfi, F., van de Braak, L. & Woensdregt, M. From Empirical Problem-Solving to Theoretical Problem-Finding Perspectives on the Cognitive Sciences. Comput Brain Behav (2024). https://doi.org/10.1007/s42113-024-00216-6

Download citation

Accepted : 06 August 2024

Published : 14 October 2024

DOI : https://doi.org/10.1007/s42113-024-00216-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Meta-theory
• Problem-finding
• Explanation
• Cognitive science
• Theoretical constraints
• Theory development
• Find a journal
• Publish with us
• Track your research

Why Kids Need More Play Time and Fewer Structured Activities

Play is critical for developing mental strength, resilience, and mental health..

Posted October 21, 2024 | Reviewed by Devon Frye

• What Is Resilience?
• Take our Resilience Test
• Find a therapist near me
• Play isn’t just fun; it’s a critical tool that fosters mental strength and emotional well-being for kids.
• Imaginative play gives children the opportunity to explore different scenarios, roles, and possibilities. 
• The confidence gained from mastering physical skills can carry over into other areas of life too.
• While it’s helpful to give kids unstructured playtime, you can also incorporate play into daily life.

Saying things like, “My child is so busy,” has become a bit of a status symbol for parents who want to raise kids who are prepared for the real world. Ironically, overscheduled kids are actually missing out on the thing they need most for their development: unstructured playtime.

Kids need time and opportunity to run around in the grass, build forts, and play dress up. Play isn’t just entertainment; it’s a critical tool that fosters mental strength and emotional well-being.

In my book, 13 Things Mentally Strong Parents Don’t Do , I share how raising strong kids sometimes involves doing less for them, not more. Allowing them to play is just one of those ways we can step back and give them the opportunity to learn about themselves, their environment, and other people.

Research Shows Play Is a Learning Tool

When your child is playing with blocks or creating some artwork, you don’t have to quiz them on what color something is for their play to become a learning experience. In fact, asking questions or insisting they do things your way might interpret their learning. Research consistently supports the importance of play in children's cognitive and emotional development.

Studies have shown that play-based learning can improve memory , language skills, and emotional regulation . Play is such a natural and effective way for children to process their experiences and emotions that many therapists use play therapy to help children work through issues. Through play, children gain a sense of control and mastery over their environment, which is foundational for mental strength.

Imaginative Play Unlocks Creativity and Problem-Solving

Imaginative play, also known as pretend play, gives children the opportunity to explore different scenarios, roles, and possibilities.

Whether they're acting as superheroes, doctors, or explorers, children use their imagination to navigate complex situations, which enhances their problem-solving skills. They may need to overcome real challenges–like how to build a castle out of pillows. Or they may tackle pretend challenges–like how to save a city from the monster.

Imaginative play encourages creativity , allowing kids to think outside the box and view challenges as opportunities rather than obstacles.

Physical Play Builds Confidence and Relieves Stress

Physical play, including activities like running, jumping, and climbing, is not only essential for physical health but also for mental strength. Physical play helps children release pent-up energy and stress , promoting relaxation and better mood regulation.

Doing the physical challenges on their own is important. Unlike a class where a coach or an instructor may give them directions on how to complete a task, unstructured play gives them the opportunity to fail, learn from their own mistakes, and try again without the pressure that they’re being judged.

The confidence gained from mastering physical skills carries over into other areas of life too. Children who have frequent opportunities and freedom to engage in physical play develop a stronger belief in their ability to overcome challenges.

Social Play Fosters Emotional Intelligence and Cooperation

Social play involves interacting with peers, which is vital for developing emotional intelligence and social skills. Through games and group activities, children learn to communicate, negotiate, and share, which are essential components of emotional resilience .

While there’s nothing wrong with team sports and adult-led opportunities for social play, opportunities to play without adult-made rules are important too. Kids need opportunities to practice their social skills—like speaking up, asking for help, or leading their peers.

Social play teaches empathy, helping children understand and respond to the emotions of others, which is crucial for building strong, supportive relationships.

Practical Tips for Incorporating Play

While some children will turn anything into an opportunity for play (including meal times), other kids may declare they’re bored when given unstructured time. Here are some practical tips for encouraging play:

• Create a play-friendly environment . Designate child-safe spaces where your children can freely engage in different types of play without the fear of breaking things or getting hurt. You don’t need to provide elaborate play sets or tons of toys. Instead, everyday objects like cardboard boxes and extra pillows can provide wonderful opportunities for play.
• Encourage unstructured play. Allow children time for free play, where they can choose activities that interest them. This can foster independence and self- motivation . Encourage them to find things to do when they’re bored.
• Involve yourself in play. Join in playtime activities, which can strengthen your bond with children and provide insight into their thoughts and feelings. Address safety concerns but try to avoid making a lot of suggestions or asking too many questions. Instead, just step into their world and play along.
• Balance screen time . While digital games can be educational, they shouldn't replace physical and imaginative play. Encourage outdoor activities and interaction with peers.
• Use play as a teaching tool. Whether you’re teaching your child how to do a new chore or you want them to learn how to invite another child to play, use play as a learning tool. Singing, storytelling, or role-playing exercises are just a few examples of fun ways to teach life skills.

Foster a Playful Environment

While it’s helpful to give kids unstructured playtime, you can also incorporate play into their daily routine. Letting them pretend they’re dressing up as a superhero when they’re getting ready for their day or allowing them to turn their snack into a dinosaur will help them thrive.

Keep in mind that learning about mental strength doesn’t have to be a sit-down lesson. Instead, it can be a playful adventure that helps them grow into confident, mentally strong adults who had plenty of free time to play.

Garrett, M. (2014). Play-based interventions and resilience in children. International Journal of Psychology and Counselling, 6(10), 133-137.

Wyver, S. R., & Spence, S. H. (1999). Play and Divergent Problem Solving: Evidence Supporting a Reciprocal Relationship. Early Education and Development , 10 (4), 419–444. https://doi.org/10.1207/s15566935eed1004_1

Amy Morin, LCSW, is a licensed clinical social worker, psychotherapist, and the author of 13 Things Mentally Strong People Don’t Do .

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• United States
• Brooklyn, NY
• Chicago, IL
• Houston, TX
• Los Angeles, CA
• New York, NY
• Portland, OR
• San Diego, CA
• San Francisco, CA
• Seattle, WA
• Washington, DC
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Self Tests NEW
• Therapy Center
• Diagnosis Dictionary
• Types of Therapy

It’s increasingly common for someone to be diagnosed with a condition such as ADHD or autism as an adult. A diagnosis often brings relief, but it can also come with as many questions as answers.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience

We’ll be at Apartmentalize, 2024 in Philadelphia. June 19-21, 2024. Schedule a Time to Meet us.

BY INDUSTRY

By audience.

Career Development Platform

Workforce skills simulations training; anytime, anywhere

Launch a job-ready certificate program for building trades

MORE FROM INTERPLAY

Workforce skills simulations training; anytime, anywhere.

• Facilities Maintenance , Multi-Family Maintenance

How to Improve Maintenance Team Problem-Solving 

• October 22, 2024

Problem-solving is an essential skill every maintenance technician should master to be effective on the job. They are constantly faced with challenges that require quick thinking and innovative solutions to not only fix an immediate issue but also identify a root cause and prevent a recurrence.

Cross-training, teaching employees skills outside their primary job functions, is the ideal solution to broaden maintenance technicians’ skills, increase their proficiency, and keep them engaged. By investing in a solution that provides various opportunities for skills growth and development, maintenance teams can improve their problem-solving capabilities, enabling them to work on a wider variety of tasks.

Understanding the Complexities of Maintenance Work

Equipment and technology are becoming increasingly complex, making routine upkeep more demanding and repairs more complicated. When maintenance teams cannot complete repairs efficiently, it increases downtime and costs.

Complexities can be compounded for maintenance teams that are managing different systems, such as HVAC, plumbing, electrical, and structural components. Each area requires specialized knowledge and skills, making relying on a single technician for all tasks difficult.

Another factor affecting complexity is that many systems are often interconnected. For example, electrical systems can be tied to HVAC controls, making diagnostics more complicated when one component fails and requires technicians to have a broad knowledge base. At the same time, uptime is critical, so maintenance techs need to be able to complete preventive maintenance, troubleshoot, and make repairs quickly and effectively.

Maximizing Your Team’s Potential

There are several benefits associated with cross-training your maintenance teams. These include:

• Increased Flexibility: A cross-trained team can fill in for each other during absences or emergencies, reducing the risk of downtime and eliminating the need to hire outside help.
• Less Outsourcing: Cross-trained workers who are confident with multiple systems are better equipped to handle repairs on their own, reducing the need for calling third-party providers, helping to cut costs, and streamlining the workflow. Maintenance technicians who are confident across multiple systems can address issues independently, preventing delays and improving uptime.
• Innovative Thinking: Exposure to different types of work and systems encourages critical thinking and strengthens troubleshooting skills, leading to faster diagnosis and repairs. Maintenance technicians also better understand how different systems interconnect, which can streamline repairs. For example, an HVAC specialist might notice plumbing issues that could be impacted by temperature changes, allowing for a proactive approach that reduces the risk of future problems.
• Stronger Teams: Cross-trained workers have a better understanding of what other people within the company do, which can break down silos, improve communication, and lead to more effective teamwork.
• Greater Job Satisfaction and Employee Retention: Cross-training demonstrates that you value your employees’ development, leading to increased job satisfaction and retention. Plus, cross-trained employees can adapt to unexpected situations more effectively and typically feel more prepared at work, helping to improve their overall job satisfaction.

Making a Cross-Training Program a Success

You can use several strategies to ensure your cross-training program is a success. When rolling out your training, steps to consider include:

• Establish the Program’s Goals: List the skills and core competencies each team member should learn based on the team’s operational needs. A good place to start is determining which skills are the most important for your operations and which positions or tasks would benefit from more coverage. Prioritize high-risk or high-frequency tasks where cross-training could have the most impact.
• Conduct Training Needs Assessments: Assessing your maintenance techs’ strengths and weaknesses can help you identify gaps in knowledge or where specialized skills are needed so you can gear training toward each individual’s needs. That avoids wasting your team’s time training on things they already know while also ensuring no critical skills are missed.
• Incorporate Hands-On Learning and Simulations: Simulations offer hands-on learning in a virtual environment so your team can practice tasks without the risk of damaging equipment or injuring themselves. Modern simulations use advanced software to create highly realistic and immersive experiences that replicate real-world scenarios. Plus, they are highly scalable and can be customized to fit your specific needs.
• Implement a Schedule: A schedule can ensure your team has time to focus on training and complete training modules. There are also opportunities to create specific pathways for advancement or training certifications, which will help technicians visualize the career benefits and advantages of completing their training.
• Create a Culture of Continuous Learning: Cross-training should not be a one-off event. Provide ongoing learning opportunities like refresher courses, advanced training, or certifications. Regularly update the training program to incorporate new technologies, techniques, or changes in industry standards. You can also implement gamification or offer incentives to increase engagement and motivation.
• Create a Feedback Loop : Schedule check-ins with team members to discuss their training experiences and track their development. Encourage employees and their managers to share feedback on the training and the overall training program. Then, use the feedback to refine the program as needed.

Measuring the Impact of Cross-Training

Measuring the success of a cross-training program can help you gauge the return on investment and quantify the program’s impact on operational efficiency, workforce capability, and overall team performance. Some key performance indicators worth tracking include:

• Skill Coverage Rate: Tracking the percentage of team members proficient in multiple essential tasks or skills can help demonstrate how well your cross-training program increases your team’s versatility. A higher skill coverage rate means more team members can handle different responsibilities, reducing the risk of downtime and inefficiencies. As skills gaps shrink, you should also see fewer tasks dependent on specific employees, improving operational resilience.
• Reduced Downtime: Cross-training aims to mitigate downtime by ensuring that maintenance tasks can be handled by multiple team members, regardless of who is on duty. You can track downtime incidents and correlate them with personnel availability. A reduction in downtime, especially during times of employee absence, indicates a program is working.
• Work Order Completion Rate: A team with more versatile skills can complete work orders more quickly and efficiently, leading to higher completion rates within a specific timeframe. Monitor the number of work orders completed on time and compare it to previous periods before cross-training was implemented.
• Employee Utilization Rate: A well-implemented cross-training program allows employees to be more productive by completing tasks outside their primary role when needed. Analyze employee time logs or productivity tracking tools to measure the time spent on value-added activities.
• Employee Engagement and Job Satisfaction: Cross-training can lead to higher job satisfaction as employees feel more valued and see opportunities for career growth within the company. Use employee surveys, interviews, or feedback forms to gauge job satisfaction. You can also track your turnover rates and internal promotions. Employees who are more engaged are less likely to leave your company.
• Number of Safety Incidents: Effective cross-training should emphasize safe practices and reduce the likelihood of on-the-job accidents. Monitor safety reports to determine if incidents decrease as employees become better trained in various tasks and safety protocols.

Let Us Help

Interplay offers immersive, on-demand, and scalable solutions to cross-train techs faster, upskill experienced techs, and provide opportunities for career advancement. If you’re ready to increase your technicians’ versatility, improve employee engagement, and reduce downtime, contact us to learn more .

Boosting Your Bottom Line: How to Maximize Training ROI

OPTIMIZING YOUR TRAINING PROGRAM

Implementing Constructivist Pedagogy in Trades Education: Remington College’s Success with Interplay Learning

The Crucial Role of Safety Training in HVAC, Plumbing, and Electrical Work

Schedule time with a training consultant to learn how you can make online skilled trades training faster, better, and easier.

Stay in-the-know

Contact sales.

Course Catalog

Certifications & Accreditations

How It Works

Commercial HVAC

Multi-Family Maintenance

Facilities Maintenance

Individuals

Workforce Development

Meet the Experts

Partners & Affiliates

Manage Cookie Consent

Privacy overview.

Filter year:

Multiply by 10 Reasoning and Problem Solving

Develop the learning of multiplying by 10 with our Year 4 multiply by 10 reasoning and problem solving resource.

This three way differentiated resource is a great way of supporting children with their reasoning and problem solving skills. Each worksheet includes four reasoning and two problem solving question. Children will have many chances to explore and deepen their learning of multiplying by 10. As well as differentiated resources, we've included the answer sheet so the hard work is done for you.

Developing : Questions to support multiplying up to 3-digit numbers by 10. Using place value counters.

Expected : Questions to support multiplying up to 3-digit numbers by 10 including using knowledge of commutative law. Using some pictorial representations.

Greater Depth : Questions to support multiplying up to 3-digit numbers by 10 including using knowledge of commutative law. Using some mixed representations within a question and some use of unconventional partitioning.

Curriculum Objectives

• Recall multiplication and division facts for multiplication tables up to 12 × 12
• Use place value, known and derived facts to multiply and divide mentally, including: multiplying by 0 and 1; dividing by 1; multiplying together three numbers

Multiplication and Division

More like this

More Y4 resources