Divisibility Rule of 3
The divisibility rule of 3 states that if the sum of the digits of a whole number is a multiple of 3, then the original number is also divisible by 3. With the help of the multiplication table of 3 or by using skip counting by 3 (starting at 0 and adding 3) it is easy to find whether a smaller number is divisible by 3 or not. However, for larger numbers, we can check if that number is completely divisible by 3 or not without doing the actual division.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |

What is the Divisibility Rule of 3?
A whole number is said to be divisible by 3 if the sum of all digits of that whole number is a multiple of 3 or exactly divisible by 3.
Divisibility Rule of 3 with Examples
The divisibility rule for 3 can be understood with the help of the following examples.
Example: Test the divisibility of the following numbers by 3.
a) In 1377, the sum of all the digits = 1 + 3 + 7 + 7 = 18. Since 18 is divisible by 3, it means 1377 is also divisible by 3. Here, 1377 ÷ 3 = 459, where 459 is the quotient and 0 is the remainder.
b) In 2130, the sum of all the digits = 2 + 1 + 3 + 0 = 6. Since 6 is divisible by 3, it means 2130 is also divisible by 3. Here, 2130 ÷ 3 = 710, where 710 is the quotient and 0 is the remainder.
c) In 3194, the sum of all the digits = 3 + 1 + 9 + 4 = 17. Since 17 is not divisible by 3, it means 3194 is not exactly divisible by 3. Here, 3194 ÷ 3 = 1064, where 1064 is the quotient and the remainder is 2.

Divisibility Rule of 3 for Large Numbers
The divisibility rule of 3 for large numbers states that if the sum of all digits of a large number is divisible by 3 or is a multiple of 3 then we can say that the large number is also divisible by 3. Example:
a) 220077 Here, the sum of all the digits = 2 + 2 + 0 + 0 + 7 + 7 = 18. We know that 18 is divisible by 3 which means 220077 is also divisible by 3. This can be verified as follows. 220077 ÷ 3 = 73359, where 73359 is the quotient and 0 is the remainder.
b) 1121031 Here, the sum of all the digits = 1 + 1 + 2 + 1 + 0 + 3 + 1 = 9. We know that 9 is divisible by 3 which means 1121031 is also divisible by 3. This can be verified as follows. 1121031 ÷ 3 = 373677, where 373677 is the quotient and 0 is the remainder.
c) 3456194 Here, the sum of all the digits = 3 + 4 + 5 + 6 + 1 + 9 + 4 = 32. We know that 32 is not divisible by 3 which means 3456194 is not completely divisible by 3.
Divisibility Rule of 3 and 9
The divisibility rule of 3 and the divisibility rule of 9 are slightly similar. As we already discussed above that the divisibility rule or divisibility test of 3 states that if the sum of all digits of a number is divisible by 3 then the number is also divisible by 3. Just like the divisibility rule of 3, the divisibility rule of 9 states that the number is said to be divisible by 9 if the sum of all the digits of a number is divisible by 9.
For example, 52884 is divisible by 3 as the sum of all digits that is 5 + 2 + 8 + 8 + 4 = 27 is divisible by 3. Here, 52884 ÷ 3 = 17628, where 17628 is the quotient and the remainder is 0. Note that the sum of the digits of the number 27 is 2 + 7 = 9 is also divisible by 3. We can repeat this process so that we get the sum closer to 3 and find out whether the number is divisible by 3 or not.
Divisibility Test of 3 and 4
The divisibility test of 3 and the divisibility test of 4 are completely different. The divisibility test of 3 states that the number is divisible by 3 if the sum of all digits of a number is divisible by 3, whereas, the divisibility test of 4 states that the number is said to be divisible by 4 if the last two digits of the given number are zeros or the number formed by the last two digits, that is, the digit at tens place and ones place is divisible by 4.
For example, 1236 is divisible by 3 as the sum of all digits that is 1 + 2 + 3 + 6 = 12. We know that 12 is divisible by 3. Now, 1236 is divisible by 4 as the number formed by the last two digits, that is, 36 is divisible by 4. Therefore, 1236 is also divisible by 4. This can be verified as follows. 1236 ÷ 4 = 309, where 309 is the quotient and the remainder is 0.
☛ Related Topics
- Divisibility Rule of 4
- Divisibility Rule of 5
- Divisibility Rule of 6
- Divisibility Rule of 7
- Divisibility Rule of 8
- Divisibility Rule of 9
- Divisibility Rule of 11
- Divisibility Rule of 13
Divisibility Rule of 3 Examples
Example 1: For the following numbers, using the test of divisibility by 3, find out whether the numbers are divisible by 3 or not.
a.) 66 b.) 97 c.) 32
a) In number 66, the sum of all the digits is 6 + 6 = 12, which is divisible by 3. Therefore, 66 is also divisible by 3. b) In number 97, the sum of all the digits is 9 + 7 = 16, which is not divisible by 3. Therefore, 97 is not divisible by 3. c) In number 32, the sum of all the digits is 3 + 2 = 5, which is not divisible by 3. Therefore, 32 is not divisible by 3.
Example 2: Using the rule of divisibility of 3, find out whether the given large number 123456789 is divisible by 3 or not.
Solution: The sum of all the digits of 123456789 is 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. We know that 45 is divisible by 3 which means 123456789 is also divisible by 3.
Example 3: Using the rule of divisibility of 3, find out if the greatest 3-digit number is exactly divisible by 3 or not.
Solution: The greatest 3-digit number is 999. The sum of all digits of the number 999 is 9 + 9 + 9 = 27, which is divisible by 3. Therefore, 999 is also divisible by 3.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Divisibility Rule of 3
go to slide go to slide
FAQs on Divisibility Rule of 3
The divisibility rule of 3 states that a whole number is said to be divisible by 3 if the sum of all its digits is exactly divided by 3. Without performing division we can find out whether a number is divisible by 3 or not. For example, 45 is divisible by 3 because the sum of 45 is (4 + 5) = 9, which is divisible by 3. Hence, 45 is said to be divisible by 3 because it gives the quotient as 15 and the remainder as 0.
Using the Divisibility Rule of 3, Check if 120 is Divisible by 3.
First, we need to check if the sum of all the digits of the given number is divisible by 3 or not. The sum of the digits of 120 = 1+ 2 + 0 = 3. We know that 3 is divisible by 3. Thus, 120 is divisible by 3.
What is the Divisibility Rule of 3 and 4?
According to the divisibility rule of 3, a number is said to be divisible by 3 if the sum of all digits of that number is divisible by 3. For example, the number 495 is completely divisible by 3. The sum of all digits are 4 + 9 + 5 = 18 and 18 is divisible by 3. Thus, 495 is divisible by 3, where quotient = 165 and remainder = 0. Let us take another example, the number 55 is not exactly divisible by 3 as the sum of all digits of the number 55 is 5 + 5 = 10 and 10 cannot be completely divided by 3. If 55 is divided by 3 the quotient will come to 18 and the remainder will come to 1.
According to the divisibility rule of 4, if the number formed by the last two digits is divisible by 4 or the number has two zeros in the end then the number is divisible by 4. For example, 4420 is divisible by 4 as the number formed by the last two digits, that is, 20, is divisible by 4[20 ÷ 4 = 5].
How do you know if a Big Number is Divisible by 3?
According to the divisibility rule of 3, any big number is exactly divisible by 3 if the sum of the digits is a multiple of 3. For example, the number 2,146,497 is exactly divisible by 3, where quotient = 715,499 and remainder = 0. The sum of all digits is 2 + 1 + 4 + 6 + 4 + 9 + 7 = 33 and 33 is exactly divisible by 3.
Using the Divisibility Rule of 3, Check if 195 is Divisible by 3.
The divisibility rule of 3 states that if the sum of the digits of a given number is divisible by 3 then the number is also divisible by 3. So, the sum of the digits of 195 is (1 + 9 + 5) = 15, which is exactly divisible by 3. Thus, 195 is divisible by 3.
- Member login
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
Divisibility rules
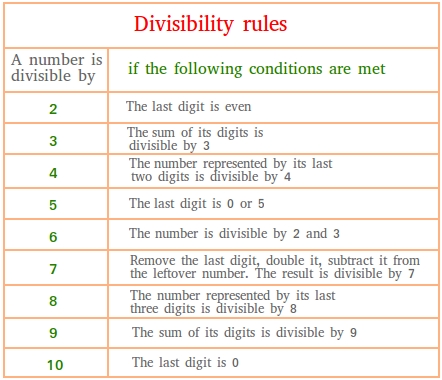
This lesson presents divisibility rules, also called divisibility tests, for the numbers 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13. Divisibility rules of whole numbers are very useful because they help us to quickly determine if a given number can be divided by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 without doing long division.
This is especially useful when dealing with large numbers and/or when you are trying to find the prime factorization of a number.
In general, a whole number x (divisor) divides another whole number y (dividend) if and only if you can find a whole number n (quotient) such that x × n = y. For instance, 12 can be divided by 3 because 3 × 4 = 12
Divisibility means that you are able to divide a number evenly. When a number can be divided evenly, the remainder is zero. For instance, 8 can be divided evenly by 4 because 8/4 = 2. However, 8 cannot be divided evenly by 3 because there will be a remainder( 2 ).
8 = 3 + 3 + 2 = 2(3) + 2
To illustrate the concept, let's say you have a cake and your cake has 8 slices, you can share that cake between you and 3 more people evenly. Each person will get 2 slices. However, if you are trying to share those 8 slices between you and 2 more people, there is no way you can do this evenly. Two people will get 3 slices of cake and one person will end up with the remainder or the leftover ( 2 ).
Divisibility rules and examples showing how to use the rules
Rule #1: divisibility by 2.
A number is divisible by 2 if its last digit is an even number or the last digit is 0,2,4,6,or 8.
For instance, 8596742 is divisible by 2 because the last digit is 2.
Rule #2: divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3. For instance, 3141 is divisible by 3 because the sum of the digits is divisible by 3. 3+1+4+1 = 9 and 9 is divisible by 3.
Rule # 3: divisibility by 4
A number is divisible by 4 if the number represented by its last two digits is divisible by 4.
For instance, 8920 is divisible by 4 because 20 is divisible by 4.
Rule #4: divisibility by 5
A number is divisible by 5 if its last digit is 0 or 5. For instance, 9564655 is divisible by 5 because the last digit is 5.
Rule # 5: divisibility by 6
A number is divisible by 6 if it is divisible by 2 and 3. Be careful! it is not one or the other. The number must be divisible by both 2 and 3 before you can conclude that it is divisible by 6.
Rule # 6: divisibility by 7
To check divisibility by 7, subtract the double of the last digit from the remaining digits. If the difference is divisible by 7, then the original number is also divisible by 7. Repeat if necessary if the number is too big.
Is 348 divisible by 7? Remove the last digit, which is 8. The remaining digits are 34. Double 8 to get 16 and subtract 16 from 34. 34 − 16 = 18 and 18 is not divisible by 7. Therefore, 348 is not divisible by 7. Is 37961 divisible by 7? Remove the last digit, which is 1. The remaining digits are 3796. Double 1 to get 2 and subtract 2 from 3796. 3796 − 2 = 3794 and 3794 is still too big. Thus repeat the process. Remove the last digit, which is 4. The remaining digits are 379. Double 4 to get 8 and subtract 8 from 379. 379 − 8 = 371 and 371 is still too big. Thus repeat the process. Remove the last digit, which is 1. The remaining digits are 37. Double 1 to get 2 and subtract 2 from 37. 37 − 2 = 35 and 35 is divisible by 7. Therefore, 37961 is divisible by 7.
Rule #7: divisibility by 8
A number is divisible by 8 if the number represented by its last three digits is divisible by 8. For instance, 587320 is divisible by 8 because 320 is divisible by 8.
Rule #8: divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9. For instance, 3141 is divisible by 9 because 3+1+4+1 = 9 and 9 is divisible by 9.
Rule # 9: divisibility by 10
A number is divisible by 10 if its last digit or the digit in the ones place is 0.
For instance, 522480 is divisible by 10 because the last digit is 0.
Other important divisibility tests
Rule # 10: divisibility by 11.
There are a couple of ways to determine divisibility by 11.
Subtract the last digit of the number from the rest of the number . If the difference is divisible by 11, then the entire number is also divisible by 11. Repeat if necessary until you get a two-digit number or a number that you can easily divide by 11.
For example, is 12 1 divisible by 11?
Subtract 1 from 12
Since 12 - 1 = 11 and 11 is divisible by 11, 121 is also divisible by 11.
Is 136 4 divisible by 11?
Subtract 4 from 136
136 - 4 = 13 2
Since 13 - 2 = 11 and 11 is divisible by 11, 1364 is also divisible by 11.
If the difference of the sum of alternative digits of a number is divisible by 11, then the entire number is divisible by 11.
Is 8 1 9 5 divisible by 11?
Alternative digits are ( 8 and 9 ) and ( 1 and 5 )
Just add them and then subtract
17 - 6 = 11
Since 11 is divisible by 11, 8195 is also divisible by 11.
Is 8 1 9 7 2 divisible by 11?
Alternative digits are ( 8 , 9 , and 2 ) and ( 1 and 7 )
8 + 9 + 2 = 19
19 - 8 = 11
Since 11 is divisible by 11, 81972 is also divisible by 11.
Rule # 11: divisibility by 12
A number is divisible by 12 if the number is divisible by both 3 and 4.
Is 180 is divisible 12?
180 is divisible by 3 since 1 + 8 + 0 = 9 and 9 is divisible 3.
180 is divisible by 4 since 80 is divisible by 4.
Therefore, 180 is divisible by 12.
Rule # 12: divisibility by 13
Add four times of the last digit of the number to the remaining number. Repeat the process if necessary until you get a number with two digits. If the number you end up with is divisible by 13, then the original number is also divisible by 13.
Is 156 divisible by 13?
24 + 15 = 39
Since 39 is divisible by 13, 156 is also divisible by 13.
Take the following divisibility rules quiz to see how well you understand the lesson on this page
Divisibility rules game
Applied math
Calculators.
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved

Rules of Divisibility: Definition, Chart, Examples
What are divisibility rules, divisibility rules: definition, divisibility test (division rules in math), divisibility rules: chart, solved examples for divisibility rules, frequently asked questions on divisibility rules.
Divisibility rules are simple tips and tricks that are used to check or test whether a number is divisible by another number.
Consider an example. Imagine that you have 13 candy bars. Can you divide them equally among 3 friends? How would you check? You can check if 13 is “divisible by” 3. In other words, you can check if 13 appears in the times table of 3 or not!
What if you wish to check if you can divide 221 candies equally among 6 friends? Finding 221 in the multiplication table of 6 can be very time-consuming. When dealing with large numbers, we need to take a different approach. What do you think?
To solve problems like these in no time, we use divisibility rules. With divisibility rules at your fingertips, you can answer easily without doing too much calculation!
Divisibility rules are a set of general rules that are often used to determine whether or not a number is absolutely divisible by another number . Note that “divisible by” means a number divides the given number without any remainder, and the answer is a whole number.
Recommended Worksheets

More Worksheets
Mathematical tests for divisibility or division rules help you employ a quick check to determine whether a number will be totally divisible by another number.
What are the divisibility rules? Let’s learn divisibility rules 1-13.
Divisibility Rule of 1
Every number ever is divisible by 1.
Divisibility Rule of 2
Every even number is divisible by 2. Any number that ends with 2, 4, 6, 8, or 0 gives 0 as the remainder when divided by 2.
For example, 12, 46, and 780 are all divisible by 2.
Divisibility Rules of 3
A number is completely divisible by 3 if the sum of its digits is divisible by 3. You can also repeat this rule until you get a single-digit sum.
Example 1: Check whether 93 is divisible by 3 or not.
Sum of the digits = 9 + 3 = 12
If the sum is a multiple of 3, then the original number is also divisible by 3.
Here, as 12 is divisible by 3, 93 is also divisible by 3.
Example 2: 45,609
To make the process even easier, you can also find the sum of the digits until you get a single digit.
Sum of digits = 4 + 5 + 6 + 9 + 0 = 24
Adding further, we get 2 + 4 = 6
6 is divisible by 3.
Thus, 45609 is divisible by 3.
Divisibility Rule of 4
If the number formed by the last two digits of a number is divisible by 4, then that number is divisible by 4. Numbers having 00 as their last digits are also divisible by 4.
Example 1: Consider the number 284. Check the last two digits.
The last two digits of the number form the number 84. As 84 is divisible by 4, the original number 284 is also divisible by 4.
Example 2: 1328

The number formed by the last 2 digits is 28.
28 is divisible by 4.
Thus, 1328 is also divisible by 4.
Divisibility Rule of 5
If a number ends with 0 or 5, it is divisible by 5.
For example, 35, 790, and 55 are all divisible by 5.
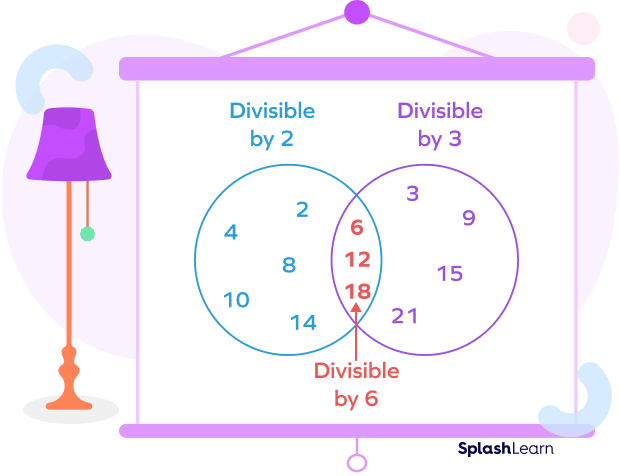
Divisibility Rule of 6
If a number is divisible by 2 and 3, it will be divisible by 6 as well.
For example, the numbers 6, 12, and 18 are divisible by 2 and 3. So, they are divisible by 6 as well.
Divisibility Rules of 7
If subtracting twice of the last digit from the number formed by remaining digits is 0 or divisible by 7, the number is divisible by 7. This one is a little tricky. Let’s understand with an example.
Example: Check whether 905 is divisible by 7 or not.
Step 1: Check the last digit and double it.
Last digit $= 5$
Multiply it by 2.
$5 \times 2 = 10$
Step 2: Subtract this product from the rest of the number.
Here, the remaining number $= 90$
$90 \;-\; 10 = 80$
Step 3: If this number is 0 or a multiple of 7, then the original number is also divisible by 7.
80 is not divisible by 7. So, 905 is also not divisible by 7.
Divisibility Rule of 8
If the number formed by the last three digits of a number is divisible by 8, we say that the number is divisible by 8.
Example 1: In the number 4176, the last 3 digits are 176.
If we divide 176 by 8, we get:
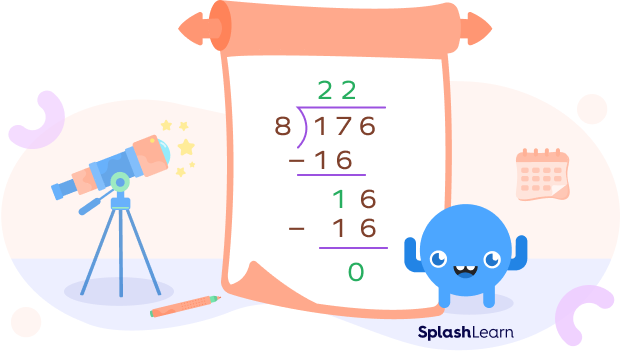
Since 176 is divisible by 8, 4176 is also divisible by 8.
Example 2:

Thus, 12,920 is divisible by 8.
Divisibility Rule of 9
If the sum of digits of the number is divisible by 9, then the number itself is divisible by 9. You can keep adding further by repeating the rule. If the single-digit sum is 9, the number is divisible by 9.
Example 1: Consider 189.
The sum of its digits$ = (1+8+9) = 18$, which is divisible by 9, hence 189 is divisible by 9.
Example 2: 12,897
Sum of digits $= 1 + 2 + 8 + 9 + 7 = 27$
Adding further, $2 + 7 = 9$
Thus, 12897 is divisible by 9.
Divisibility Rule of 10
Any number whose last digit is 0 is divisible by 10.
Example: 10, 20, 30, 100, 2000, 40,000, etc.
Divisibility Rule for 11
If the difference of the sum of alternative digits of a number is divisible by 11, then that number is divisible by 11.
Example 1: Consider the number. 2846767. First, understand the digit positions. We find two sums: the sum of digits at the even places and the sum of digits at the odd places.
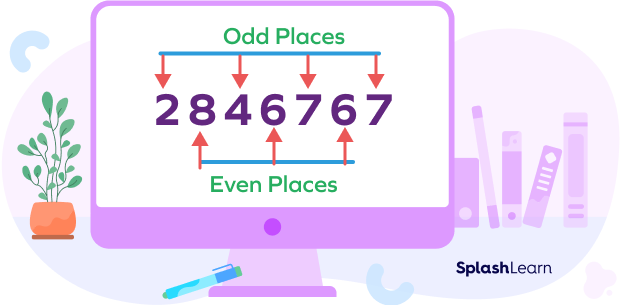
Sum of digits at even places (From right) $= 8 + 6 + 6 = 20$
Sum of digits at odd places (From right) $= 7 + 7 + 4 + 2 = 20$
Difference $= 20 – 20 = 0$
Difference is divisible by 11.
Thus, 2846767 is divisible by 11.
Example 2: Is 61809 divisible by 11?
Identify digits in odd places and digits in even places.
Here, $6 + 8 + 9 = 23$ and $0 + 1 = 1$
Difference $= 23 – 1 = 22$
22 is divisible by 11.
Thus, the given number is divisible by 11.
Another Divisibility Rule For 11
There’s another simple divisibility rule for 11.
Subtract the last digits from the remaining number. Keep doing this until we get a two-digit number. If the number obtained is divisible by 11, the original number is divisible by 11.
Example: 1749
$174\;-\;9 = 165$
$16\;-\;5 = 11$ … divisible by 11
Thus, 1749 is divisible by 11.
Divisibility Rule of 12
If the number is divisible by both 3 and 4, then the number is divisible by 12
Example: 4880
Sum of the digits $= 4 + 8 + 8 + 0 = 20$ (not a multiple of 3)
Last two digits $= 80$ (divisible by 4)
The given number 4880 is divisible by 4 but not by 3.
Thus, 4880 is not divisible by 12.
Divisibility Rules of 13
To check if it is divisible by 13, we add 4 times of the last digit of the remaining number and repeat the process until we get a two-digit number. If that two-digit number is divisible by 13, then the given number is divisible by 13.
Example: Is 4186 divisible by 13?
- $418 + (6 \times 4) = 418 + 24 = 442$
- $44 + (2 \times 4) = 44 + 8 = 52$
52 is divisible by 13 since $13 \times 4 = 52$.
Thus, 4186 is divisible by 13.
| Every number is divisible by 1. | |
| When the last digit is 0, 2, 4, 6, or 8 | |
| When the sum of digits is divisible by 3 | |
| When the last two digits of any dividend are divisible by 4 Numbers having 00 as their last digits are also divisible by 4.) | |
| When the last digit is either 0 or 5 | |
| When the number is divisible by both 2 and 3 | |
| When the last digit is subtracted twice from the remaining digits and gives the multiple of 7 | |
| When the last three digits are divisible by 8 Numbers having 000 as their last digits are also divisible by 8.) | |
| When the sum of all digits is divisible by 9 | |
| When the last digit is 0 | |
| When the difference between the sums of the alternative digits is divisible by 11 | |
| When a number is both divisible by 3 and 4 | |
| Multiply 4 with the last digit and add this product to the remaining number. Continue till a two-digit number is found. If the 2-digit number is divisible by 13, the number is divisible by 13. | |
Facts about Divisibility Rules
- “Divisible” means a number can be divided evenly with another number with NO remainders.
- The divisibility rule is a shortcut to analyze whether an integer is completely divisible by a number without actually doing the calculation.
- Zero is divisible by any number (except by itself), so it gets a “yes” to all these tests.
- When a number is divisible by another number, it is also divisible by each of the factors of that number. For instance, a number divisible by 6 will also be divisible by 2 and 3. A number divisible by 10 is also divisible by 5 and 2.
- Numbers that have two zeros at the end are divisible by 4. Numbers with three zeros at the end are divisible by 8.
- The number 2,520 is the smallest number that is divisible by 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In this article, we have learned divisibility rules and charts with examples. Let’s solve some divisibility rules examples to understand it better.
1. If a number is divisible by 6, can we say it is divisible by 2 as well?
Solution:
Yes, because 6 is divisible by 2.
If a number is divisible by some numbers, say x, that number is also divisible by factors of x.
For example, 480 is divisible by 6.
Thus, $480 \div 6 = 80$.
$480 \div 2 = 240$.
Also, $480 \div 3 = 160$
Thus, If a number is divisible by 6, can we say it is divisible by 2 and 3 as well, as 2 and 3 are factors of 6.
2. Use divisibility rules to check whether 642 is divisible by 4 and 3.
Divisibility rule for 4: If the last two digits of a number are divisible by 4, then that number is divisible by 4.
The last two digits of $642 = 42$, which is not divisible by 4.
Thus, 542 is not divisible by 4.
Divisibility rule of 3: If the sum of digits is divisible by 3, we say that the original number is divisible by 3.
Sum of digits $= 6 + 4 + 2 = 12$
12 is divisible by 3.
So, 542 is not divisible by 8.
3. Check 3640 for divisibility by 13.
The last number of the given number is 0.
Multiply 4 by 0 and add to the rest of the number.
$364 + (0 \times 4) = 364$.
Again, multiply 4 by the last digit of the obtained three-digit number and add to the rest of the digits as
$36 + (4 \times 4) = 52$
Now, we obtained a two-digit number 52, which is divisible by 13.
$52 = 4 \times 13$
Hence, 3640 is divisible by 13.
Attend this quiz & Test your knowledge.
Which number is not divisible by 5?
Which of the following numbers is divisible by 2, which of the following numbers is divisible by 6, identify a number divisible by 9..
What are co-primes and their divisibility rules?
Co-primes are a pair of numbers that have 1 as the common factor. If the number is divisible by such co-primes, the number is also a divisible by-product of the co-primes. For example, 14 is divisible by both 2 and 7. They are co-primes that have only 1 as the common factor, so the number is divided by 14, the product of 2 and 7.
When is a number said to be a factor of another number?
A number x is said to be a factor of number y if y is divisible by x. For example, 10 is divisible by 2, so 2 is a factor of 10.
Where do we use divisibility rules in real life?
Divisibility rules are the quickest way to determine if a number is divisible by another number. It saves the time required to perform the actual division. Divisibility rules also give you a number sense when it comes to division and multiplication of two or more numbers.
What are composite numbers?
In math, composite numbers can be defined as numbers that have more than two factors. Numbers that are not prime are composite numbers because they are divisible by more than two numbers.
For example:
Factors of $4 = 1, 2, 4$, i.e.,
Since 4 has more than two factors, 4 is a composite number.
How many divisibility rules are there?
We often have standards for divisibility from 1 to 20. However, if we were able to recognize the pattern of multiples of integers, we could develop further tests for divisibility. For example, the divisibility rule of 21 states that a number must be divisible by both 3 and 7. It is because 21 is a multiple of two prime numbers 3 and 7, so all the multiples of 21 will definitely have 3 and 7 as their common factors.
RELATED POSTS
- Dividing Mixed Numbers
- Degree of a Polynomial: Definition, Types, Examples, Facts, FAQs
- Volume of a Prism – Definition With Examples
- Base Area of a Cylinder – Definition, Formula, Examples, FAQs
- Area in Math – Definition, Composite Figures, FAQs, Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Divisibility Rules
Easily test if one number can be exactly divided by another
Divisible By
"Divisible By" means "when you divide one number by another the result is a whole number "
14 is divisible by 7, because 14 ÷ 7 = 2 exactly
15 is not divisible by 7, because 15 ÷ 7 = 2 1 7 (the result is not a whole number)
0 is divisible by 7, because 0 ÷ 7 = 0 exactly (0 is a whole number)
The Divisibility Rules
These rules let you test if one number is divisible by another, without having to do too much calculation!
Example: is 723 divisible by 3?
We could try dividing 723 by 3
Or use the "3" rule: 7+2+3=12, and 12 ÷ 3 = 4 exactly Yes
Note: Zero is divisible by any number (except by itself), so gets a "yes" to all these tests.
Any integer (not a fraction) is divisible by 1
The last digit is even (0,2,4,6,8)
12 8 Yes
12 9 No
The sum of the digits is divisible by 3
381 (3+8+1=12, and 12÷3 = 4) Yes
217 (2+1+7=10, and 10÷3 = 3 1 / 3 ) No
This rule can be repeated when needed:
99996 (9+9+9+9+6 = 42, then 4+2=6) Yes
The last 2 digits are divisible by 4
13 12 is (12÷4=3) Yes
70 19 is not (19÷4=4 3 / 4 ) No
We can also subtract 20 as many times as we want before checking:
68: subtract 3 lots of 20 and we get 8 Yes
102: subtract 5 lots of 20 and we get 2 No
Another method is to halve the number twice and see if the result is still a whole number:
124/2 = 62, 62/2 = 31, and 31 is a whole number. Yes
30/2 = 15, 15/2 = 7.5 which is not a whole number. No
The last digit is 0 or 5
17 5 Yes
80 9 No
Is even and is divisible by 3 (it passes both the 2 rule and 3 rule above)
114 (it is even, and 1+1+4=6 and 6÷3 = 2) Yes
308 (it is even, but 3+0+8=11 and 11÷3 = 3 2 / 3 ) No
Double the last digit and subtract it from a number made by the other digits. The result must be divisible by 7. (We can apply this rule to that answer again)
672 (Double 2 is 4, 67−4=63, and 63÷7=9) Yes
105 (Double 5 is 10, 10−10=0, and 0 is divisible by 7) Yes
905 (Double 5 is 10, 90−10=80, and 80÷7=11 3 / 7 ) No
The last three digits are divisible by 8
109 816 (816÷8=102) Yes
216 302 (302÷8=37 3 / 4 ) No
A quick check is to halve three times and the result is still a whole number:
816/2 = 408, 408/2 = 204, 204/2 = 102 Yes
302/2 = 151, 151/2 = 75.5 No
The sum of the digits is divisible by 9 (Note: This rule can be repeated when needed)
1629 (1+6+2+9=18, and again, 1+8=9) Yes
2013 (2+0+1+3=6) No
The number ends in 0
22 0 Yes
22 1 No
Add and subtract digits in an alternating pattern (add digit, subtract next digit, add next digit, etc). Then check if that answer is divisible by 11.
1 3 6 4 (+1−3+6−4 = 0 ) Yes
9 1 3 (+9−1+3 = 11 ) Yes
3 7 2 9 (+3−7+2−9 = −11 ) Yes
9 8 7 (+9−8+7 = 8 ) No
The number is divisible by both 3 and 4 (it passes both the 3 rule and 4 rule above)
648 ( By 3? 6+4+8=18 and 18÷3=6 Yes) (By 4? 48÷4=12 Yes) Both pass, so Yes
524 ( By 3? 5+2+4=11, 11÷3= 3 2 / 3 No) (Don't need to check by 4) No
There are lots more! Not only are there divisibility tests for larger numbers, but there are more tests for the numbers we have shown.
Factors Can Be Useful
Factors are the numbers you multiply to get another number:
This can be useful, because:
When a number is divisible by another number ...
... then it is also divisible by each of the factors of that number.
Example: If a number is divisible by 6, it is also divisible by 2 and 3
Example: If a number is divisible by 12, it is also divisible by 2, 3, 4 and 6
Another Rule For 11
- Subtract the last digit from a number made by the other digits.
- If that number is divisible by 11 then the original number is, too.
Can repeat this if needed,
Example: 286
28 − 6 is 22, which is divisible by 11, so 286 is divisible by 11
Example: 14641
- 1464 − 1 is 1463
- 146 − 3 is 143
- 14 − 3 is 11, which is divisible by 11, so 14641 is divisible by 11
The Rules of Divisibility
Lessons with videos, examples, solutions and stories to help students learn the Divisibility Rules.
Related Pages Basic Divisibility Rules Divisibility Rules Explained More Lessons for Arithmetic Free Math Worksheets
The multiple of a number is always divisible by the number. The word “divisible” means that it can be divided exactly.
Example: 144 ÷ 4 = 36 (remainder = 0). So, 144 is divisible by 4 and is a multiple of 4.
144 ÷ 5 = 28 (remainder = 4). So, 144 is not divisible by 5 and is not a multiple of 5.
What are the Divisibility Rules? The following table gives criteria or conditions to test divisibility of any number by the numbers listed in the first column. This is useful when testing the divisibility of large numbers and to determine whether a number is a multiple of another.
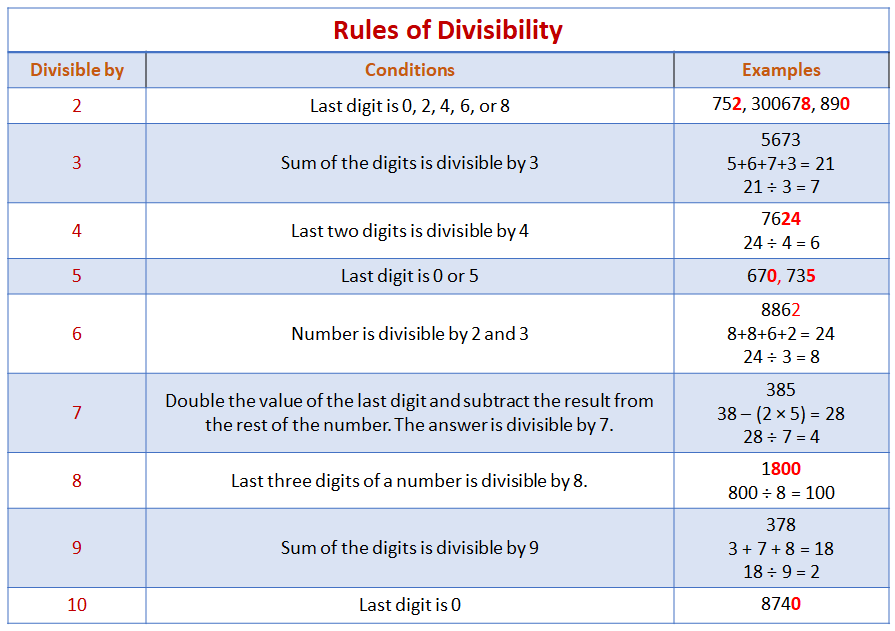
A number is divisible by 2 if its last digit is 0, 2, 4, 6 or 8. A number is divisible by 3 if the sum of all its digits is divisible by 3. A number is divisible by 4 if its last two digits is divisible by 4. A number is divisible by 5 if its last digit is 0 or 5. A number is divisible by 6 if it is divisible by 2 and 3. A number is divisible by 7 if we double the value of the last digit and subtract the result from the rest of the number. The answer is divisible by 7. A number is divisible by 8 if its last three digits is divisible by 8. A number is divisible by 9 if the sum of all its digits is divisible by 9. A number is divisible by 10 if its last digit is 0.
Example: Check whether 171 is a multiple of 9.
Solution: Sum of digits 1 + 7 + 1 = 9 9 ÷ 9 = 1
So, 171 is a multiple of 9
The following video describes the rules of divisibility.
A song to help you remember the divisibility rules.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Divisibility Rule of 3

The divisibility rule of 3 helps to check whether the given number is divisible by three or not. For small numbers, we can easily conclude the divisibility by 3. In the case of larger numbers, it is not possible to check the divisibility just by looking at the numbers. Thus, we require a specific rule that can be employed for all the numbers to check for the divisibility by 3. In this article, you will learn the divisibility rule of 3, along with solved examples.
Learn: Divisibility rules
What is the Divisibility Rule of 3?
The divisibility rule of 3 states that if the sum of digits of a number is a multiple of 3, the number will be completely divisible by 3.

Click here to learn what digits and numbers are.
Proof of Divisibility Rule of 3
We can prove the divisibility rule of 3 with the help of an example.
Consider the number 4368.
Let us expand this number as given below:
4368 = 4 × 1000 + 3 × 100 + 6 × 10 + 8 × 1
= 4 × (999 + 1) + 3 × (99 + 1) + 6 × (9 + 1) + 8 × 1
= (4 × 999 + 3 × 99 + 6 × 9) + (4 × 1 + 3 × 1 + 6 × 1 + 8 × 1)
= (4 × 999 + 3 × 99 + 6 × 9) + (4 + 3 + 6 + 8)
We know that 9, 99, 999,… are divisible by 3, and thus the multiples of these numbers are also divisible by 3.
So, the divisibility of 4368 is now dependent on the sum 4 + 3 + 6 + 8.
Here, 4, 3, 6 and 8 are the digits of the number 4368.
From the above, we can say that if the sum of these digits is divisible by 3 or a multiple of 3, the number 4368 is divisible by 3.
Hence, we can conclude that if the sum of digits of a number is divisible by 3 or a multiple of 3, the number is divisible by 3.
|
|
|---|
Divisibility Rule of 3 and 9
The divisibility rules for 3 and 9 are quite similar. As defined above, if the sum of the digits of a number is a multiple of 3 or divisible by 3, then the number is divisible by 3. Similarly, if the sum of the digits of a number is a multiple of 9 or divisible by 9, then the number is divisible by 9.
Watch The Below Video to Learn More About Divisibility Rule of 3 and 9

Examples on Divisibility Rule of 3
Question 1:
Is 53472 divisible by 3?
Given number: 53472
Let us add the digits of the given number.
5 + 3 + 4 + 7 + 2 = 21 (multiple of 3, since 3 × 7 = 21)
Therefore, 53472 is divisible by 3.
Question 2:
Check whether the number 6874 is divisible by 3.
Given number: 6874
6 + 8 + 7 + 4 = 25 (not a multiple of 3, since 3 × 8 = 24 but 25 = 3 × 8 + 1)
Therefore, 6874 is not divisible by 3.
Frequently Asked Questions on Divisibility Rule of 3
Write the divisibility rule of 3., explain the divisibility rule of 3 with an example..
Consider the number 728. Let us find the sum of digits of this number. 7 + 2 + 8 = 17 (not a multiple of 3) Here, the sum of digits is neither a multiple of 3 nor divisible by 3. Hence, by the divisibility rule of 3, we can say that 728 is not divisible by 3.
How do you say whether the given number is divisible by 3?
By the divisibility rule of 3, we can conclude whether the given number is divisible by 3. So, if any number is divisible 3, then the sum of digits of such a number must be divisible by 3 or multiple of 3.

Is 81 divisible by 3?
Yes, 81 is divisible by 3. This can be justified by the divisibility rule of 3. 8 + 1 = 9 (multiple of 3) So, the number 81 is divisible by 3.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Reset password New user? Sign up
Existing user? Log in
Proof Of Divisibility Rules
Already have an account? Log in here.
Recommended Course
Number theory.
Explore the powers of divisibility, modular arithmetic, and infinity.
Main article: Divisibility Rules
Divisibility rules are efficient shortcut methods to check whether a given number is completely divisible by another number or not. These divisibility tests, though initially made only for the set of natural numbers \((\mathbb N),\) can be applied to the set of all integers \((\mathbb Z)\) as well if we just ignore the signs and employ our divisibility rules. Note that the term "complete divisibility" means that one of the numbers with the smaller magnitude must be a divisor of the one with the greater magnitude.
But from where do these divisibility rules come from? How can we be so sure that it will work for every integer? Let us unveil the answers to all these questions as we explore the underlying principles behind this set of rules based on deductive reasoning and our knowledge of modular arithmetic .
Divisibility Rules for some Selected Integers
Divisibility by 2 (similar for 5 and 10), divisibility by 3 (similar for 9), divisibility by 4 (similar for 25), divisibility by 6, divisibility by 7, divisibility by 8 (similar for 125), divisibility by 11, divisibility by 12, divisibility by 13.
- Divisibility by 1: Every number is divisible by \(1\).
- Divisibility by 2: The number should have \(0, \ 2, \ 4, \ 6,\) or \(8\) as the units digit.
- Divisibility by 3: The sum of digits of the number must be divisible by \(3\).
- Divisibility by 4: The number formed by the tens and units digit of the number must be divisible by \(4\).
- Divisibility by 5: The number should have \(0\) or \(5\) as the units digit.
- Divisibility by 6: The number should be divisible by both \(2\) and \(3\).
- Divisibility by 7: The absolute difference between twice the units digit and the number formed by the rest of the digits must be divisible by \(7\) (this process can be repeated for many times until we arrive at a sufficiently small number).
- Divisibility by 8: The number formed by the hundreds, tens and units digit of the number must be divisible by \(8\).
- Divisibility by 9: The sum of digits of the number must be divisible by \(9\).
- Divisibility by 10: The number should have \(0\) as the units digit.
- Divisibility by 11: The absolute difference between the sum of alternate pairs of digits must be divisible by \(11\).
- Divisibility by 12: The number should be divisible by both \(3\) and \(4\).
- Divisibility by 13: The sum of four times the units digits with the number formed by the rest of the digits must be divisible by \(13\) (this process can be repeated for many times until we arrive at a sufficiently small number).
- Divisibility by 25: The number formed by the tens and units digit of the number must be divisible by \(25\).
- Divisibility by 125: The number formed by the hundreds, tens and units digit of the number must be divisible by \(125\).
Now, we will be discussing the derivations of these rules. In every proof, the variable will take the form
\[ N = \overline {a_n a_{n-1} a_{n-2} \ldots a_2 a_1 a_0}\]
\[\text{or}\]
\[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0.\]
Any number with \(2, 4, 6, 8,\) or \(0\) as the units digit is divisible by \(2\).
Prove that the number \(506\) is divisible by \(2\) because \(6\) is divisible by \(2\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Taking mod 2 of \(N,\) we get \[\begin{align} N & \equiv 0+0+0+ \cdots +0+0+ a_0 \pmod{2} \qquad \big(\text{as } 10^k, \text{ where } k \ge 1, \text{ is always divisible by } 2\big)\\ & \equiv a_0 \pmod{2}. \end{align}\] Therefore, \(N \equiv 0 \pmod{2}\) if \(a_0 \equiv 0 \pmod{2}\). Since, \(a_0\) is a single-digit number, the only values that satisfy this condition are \(0, 2, 4, 6,\) and \(8\). \(_\square\) The same approach can be used for \(5\) and \(10\) as well due to the fact that \(10^k,\) where \(k \ge 1,\) is always divisible by \(5\) and \(10\) as well and hence the values fitting for \(a_0\) in this case are \(0\) and \(5\) for the number \(5\) and \(0\) for the number \(10\), thus proving the divisibility tests of \(5\) and \(10\).
Any number whose sum of digits is divisible by \(3\) is also divisible by \(3\).
Prove that the number \(168\) is divisible by \(3\) because \((1+6+8)=15\) is divisible by \(3\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Taking mod 3 of \(N,\) we get \[\begin{align} N \equiv & 1 \times a_n\pmod{3} + 1 \times a_{n-1}\pmod{3} + 1 \times a_{n-2}\pmod{3} \\ & + \cdots + 1 \times a_2\pmod{3} + 1 \times a_1\pmod{3} + 1 \times a_0\pmod{3} \qquad \big(\text{as } 10^k-1, \text{ where } k \ge 1, \text{ is always divisible by } 3\big)\\ \\ \equiv &\left( a_n + a_{n-1} + a_{n-2} + \cdots + a_2 + a_1 + a_0 \right) \pmod{3}. \end{align}\] Therefore, \(N \equiv 0 \pmod{3}\) if \( a_n + a_{n-1} + a_{n-2} + \cdots + a_2 + a_1 + a_0 \equiv 0 \pmod{3}\). Thus, the sum of digits must be divisible by \(3\) for the number to be divisible by \(3\). \(_\square\) The same approach can be used for \(9\) as well due to the fact that \(10^k - 1,\) where \(k \ge 1,\) is always divisible by \(9\) as well and hence the sum of digits of the number in this case must be divisible by \(9\) so that the number itself is divisible by \(9\), thus proving the divisibility test of \(9\).
Any number whose digits in the tens and units places taken in that order are divisible by \(4\) is itself also divisible by \(4\).
Prove that the number \(11564\) is divisible by \(4\) because \(64\) is divisible by \(4\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Taking mod 4 of \(N,\) we get \[\begin{align} N & \equiv 0+0+0+ \cdots +0+10 a_1+ a_0 \pmod{4} \qquad \big(\text{as } 10^k, \text{ where } k \ge 2, \text{ is always divisible by } 4\big) \\ & \equiv 10 a_1 + a_0 \pmod{4}. \end{align}\] Therefore, \(N \equiv 0 \pmod{4}\) if \(10a_1 + a_0 = \overline {a_1 a_0} \equiv 0 \pmod{4}\). Thus, if the tens and units places of a number taken in that order are divisible by \(4,\) then the number is also divisible by \(4\). \(_\square\) The same approach can be used for \(25\) as well due to the fact that \(10^k,\) where \(k \ge 2,\) is always divisible by \(25\) as well and hence if the digits in the tens and units place of a number taken in that order is divisible by \(25\), then the number is also divisible by \(25\).
Any number which is divisible by both \(2\) and \(3\) is also divisible by \(6\) as well.
Prove that the number \(678\) is divisible by \(6\) because \(678\) is divisible by both \(2\) and \(3\). This doesn't require any detailed proof other than the fact that if \(N \equiv 0 \pmod{2}\) and \(N \equiv 0 \pmod{3}\), then \(N \equiv 0 \pmod{2 \times 3 = 6}\), as \(2\) and \(3\) are coprime numbers. \(_\square\)
Any number whose absolute difference between twice the units digit and the number formed by the rest of the digits is \(0\) or divisible by \(7\) is itself divisible by \(7\).
Prove that the number \(343\) is divisible by \(7\) because \(34 - 2 \times 3 = 28\) is also divisible by \(7\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Let \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0 = 7k\] for some integer \(k.\) Then \[N = 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 \right) + a_0 = 7k.\] Add and subtract \(20 a_0\) on the LHS to get \[\begin{align} N &= 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 \right) + 20 a_0 - 20 a_0 + a_0\\ &= 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 - 2 a_0 \right) + 21 a_0 \\ &= 7k\\ 7k - 21 a_0 &=10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 - 2 a_0 \right) \\ &\equiv 0 \pmod{7}\\\\ \Rightarrow 10 \left( \overline{a_n a_{n-1} a_{n-2} \ldots a_2 a_1} - 2 a_0 \right) &\equiv 0 \pmod{7}. \end{align}\] Therefore, since \(10 \equiv 3 \pmod{7},\) for \(N\) to be divisible by \(7,\) it must be true that \(\overline{a_n a_{n-1} a_{n-2} \ldots a_2 a_1} - 2 a_0 \equiv 0 \pmod{7}\). Thus, for a number, if the absolute difference between twice the units digit and the number formed by the rest of the digits is \(0\) or divisible by \(7,\) then that number is also divisible by \(7\). \(_\square\)
Any number whose digits in the hundreds, tens, and units places taken in that order are divisible by \(8\) is itself also divisible by \(8.\)
Prove that the number \(74152\) is divisible by \(8\) because \(152\) is divisible by \(8\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Taking mod 8 of \(N,\) we get \[\begin{align} N & \equiv 0+0+0+ \cdots +10^2 a_2+10 a_1+ a_0 \pmod{8} \qquad \big(\text{as } 10^k, \text{ where } k \ge 3, \text{ is always divisible by } 8\big) \\ & \equiv 100 a_2 + 10 a_1 + a_0 \pmod{8}. \end{align}\] Therefore, \(N \equiv 0 \pmod{8}\) if \(100 a_2 + 10a_1 + a_0 = \overline {a_2 a_1 a_0} \equiv 0 \pmod{8}\). Thus, if the hundreds, tens, and units places of a number taken in that order are divisible by \(8,\) then the number is also divisible by \(8\). \(_\square\) The same approach can be used for \(125\) as well due to the fact that \(10^k,\) where \(k \ge 3,\) is always divisible by \(125\) as well and hence if the digits in the hundreds, tens, and units places of a number taken in that order are divisible by \(125\), then the number is also divisible by \(125\).
Any number whose absolute difference between the sum of digits in the even positions and the sum of digits in the odd positions is \(0\) or divisible by \(11\) is itself also divisible by \(11\).
Prove that the number \(105204\) is divisible by \(11\) because \(\big|(0+2+4)-(1+5+0)\big|=0\) is divisible by \(11\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Taking mod 11 of \(N,\) we get \[N \equiv \pm a_n \mp a_{n-1} \pm a_{n-2} \cdots \mp a_2 \pm a_1 \mp a_0 \pmod{11}. \qquad \big(\text{as } 10^k \equiv +1 \bmod{11} \text{ if } k \text{ is even, and } 10^k \equiv -1 \bmod{11} \text{ if } k \text{ is odd}\big)\] Suppose \(n\) is even, then we have \[\begin{align} N &\equiv a_n - a_{n-1} + a_{n-2} - \cdots + a_2 - a_1 + a_0 \pmod{11} \\ &\equiv \left( a_n + a_{n-2} + \cdots + a_2 + a_0 \right) - \left( a_{n-1} + a_{n-3} + \cdots + a_3 + a_1 \right) \pmod{11}. \end{align}\] Therefore, \(N \equiv 0 \pmod{11}\) if \(\left( a_n + a_{n-2} + \cdots + a_2 + a_0 \right) - \left( a_{n-1} + a_{n-3} + \cdots + a_3 + a_1 \right) \equiv 0 \pmod{11},\) given that \(n\) is even. Suppose \(n\) is odd, then we have \[\begin{align} N &\equiv -a_n + a_{n-1} - a_{n-2} + \cdots + a_2 - a_1 + a_0 \pmod{11} \\ &\equiv \left( a_{n-1} + a_{n-3} + \cdots + a_2 + a_0 \right) - \left( a_n + a_{n-2} + \cdots + a_3 + a_1 \right) \pmod{11}. \end{align}\] Therefore, \(N \equiv 0 \pmod{11}\) if \(\left( a_{n-1} + a_{n-3} + \cdots + a_2 + a_0 \right) - \left( a_n + a_{n-2} + \cdots + a_3 + a_1 \right) \equiv 0 \pmod{11},\) given that \(n\) is odd. From the above two conditions, we infer that for a number to be divisible by \(11\), its absolute difference between the sum of digits occurring in the even positions and the sum of digits occurring in odd positions should be \(0\) or divisible by \(11\). \(_\square\)
Any number which is divisible by both \(3\) and \(4\) is also divisible by \(12\) as well.
Prove that the number \(1092\) is divisible by \(12\) because \(1092\) is divisible by both \(3\) and \(4\). This also doesn't require any detailed proof other than the fact that if \(N \equiv 0 \pmod{3}\) and \(N \equiv 0 \pmod{4}\), then \(N \equiv 0 \pmod{3 \times 4 = 12},\) as \(3\) and \(4\) are coprime numbers. \(_\square\)
Any number whose sum of four times the units digit and the number formed by the rest of the digits is divisible by \(13\) is itself also divisible by \(13.\)
The number \(169\) is divisible by \(13\) because \(16 + 4 \times 9 = 52\) is also divisible by \(13\). We have \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0. \] Let \[N = 10^n a_n + 10^{n-1} a_{n-1} + 10^{n-2} a_{n-2} + \cdots + 10^2 a_2 + 10 a_1 + a_0 = 13k\] for some integer \(k.\) Then \[N = 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 \right) + a_0 = 13k.\] Add and subtract \(40 a_0\) on the LHS to get \[\begin{align} N &= 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 \right) + 40 a_0 - 40 a_0 + a_0\\ &=10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 + 4 a_0 \right) - 39 a_0 \\ &= 13k\\ 13k + 39 a_0 &= 10 \left( 10^{n-1} a_n + 10^{n-2} a_{n-1} + 10^{n-3} a_{n-2} + \cdots + 10 a_2 + a_1 + 4 a_0 \right) \\ &\equiv 0 \pmod{13}\\\\ \Rightarrow 10 \left( \overline{a_n a_{n-1} a_{n-2} \ldots a_2 a_1} + 4 a_0 \right) &\equiv 0 \pmod{13}. \end{align}\] Therefore, since \(10 \equiv 10 \pmod{13}\), for \(N\) to be divisible by \(13\), it must be true that \(\overline{a_n a_{n-1} a_{n-2} \ldots a_2 a_1} + 4 a_0 \equiv 0 \pmod{13}\). Thus, for a number, if the sum of four times its units digit and the number formed by the rest of the digits is divisible by \(13\), then that number is also divisible by \(13\). \(_\square\)
With similar logical approach, a divisibility test can be made for each and every number by just observing their pattern over successive powers of \(10\).
- SAT Math: Factors, Divisibility and Remainders
- Application of Divisibility Rules
- Divisibility Rules

Master concepts like these
Learn more in our Number Theory course, built by experts for you.
Problem Loading...
Note Loading...
Set Loading...
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Divisible by 3 | Divisibility Test for 3 | Divisibility Rule of 3 with Examples
Divisible by 3 is possible when the sum of the given digits is divisible by 3. Check out how a number is divisible by 3 in this article. We have given different examples along with a clear explanation here. Also, we have included some of the tricks to find out the process to find a number that is divisible by 3. Improve your math solving skills by learning the different tricks in Divisibility Rules . Verify all the articles on our website and make your real-life happy with the best math learning process.
- Properties of Divisibility
- Exact Divisibility
- Worksheet on Exact Divisibility
How to Test if a Number is Divisible by 3 or Not?
Follow the below procedure to find out the numbers either are divisible by 3 or not.
- Note down the given number.
- Add all the digits of a given number.
- Check out the output of addition is divisible by 3 or not.
- If the output is divisible is 3, the given number is divided by 3. If not the given number is not divisible by 3.
Divisibility Test of 3 Examples
(i) 60 Solution: The given number is 60. Add the digits of the given number. Add 6 and 0. 6 + 0 = 6. The number 6 is divisible by 3. Hence, 60 is divisible by 3.
(ii) 74 Solution: The given number is 74. Add the digits of the given number. Add 7 and 4. 7 + 4 = 11. The number 11 is not divisible by 3. Hence, 74 is not divisible by 3.
(iii) 139 Solution: The given number is 139. Add the digits of the given number. Add 1, 3, and 9. 1 + 3 + 9 = 13. The number 13 is not divisible by 3. Hence, 139 is not divisible by 3.
(iv) 234 Solution: The given number is 234. Add the digits of the given number. Add 2, 3, and 4. 2 + 3 + 4 = 9. The number 9 is divisible by 3. Hence, 234 is divisible by 3.
(v) 196 Solution: The given number is 196. Add the digits of the given number. Add 1, 9, and 6. 1 + 9 + 6 = 16. The number 16 is not divisible by 3. Hence, 196 is not divisible by 3.
(vi) 156 Solution: The given number is 156. Add the digits of the given number. Add 1, 5, and 6. 1 + 5 + 6 = 12. The number 12 is divisible by 3. Hence, 156 is divisible by 3.
(vii) 174 Solution: The given number is 174. Add the digits of the given number. Add 1, 7, and 4. 1 + 7 + 4 = 12. The number 12 is divisible by 3. Hence, 174 is divisible by 3.
(viii) 278 Solution: The given number is 278. Add the digits of the given number. Add 2, 7, and 8. 2 + 7 + 8 = 17. The number 17 is not divisible by 3.
Hence, 278 is not divisible by 3.
(ix) 279 Solution: The given number is 279. Add the digits of the given number. Add 2, 7, and 9. 2 + 7 + 9 = 18. The number 18 is divisible by 3. Hence, 279 is divisible by 3.
(x) 181 Solution: The given number is 181. Add the digits of the given number. Add 1, 8, and 1. 1 + 8 + 1 = 10. The number 10 is not divisible by 3. Hence, 181 is not divisible by 3.
Solved Problems on Rules of Divisibility by 3
Fill the correct lowest possible digit in the blank space to make the number divisible by 3.
(i) 15335_ The given number is 15335_. Add the digits of the given number. Add 1, 5, 3, 3, and 5. 1 + 5 + 3 + 3 + 5 = 17. By adding 1 to the number 17, it becomes 18. The number 18 is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 1. Hence, 153351 is the required digit of a given number.
(ii) 20_987 The given number is 20_987. Add the digits of the given number. Add 2, 0, 9, 8, and 7. 2 + 0 + 9 + 8 + 7 = 26. By adding 1 to the number 26, it becomes 27. The number 27 is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 1. Hence, 201987 is the required digit of a given number.
(iii) 8420_1 The given number is 8420_1. Add the digits of the given number. Add 8, 4, 2, 0, and 1. 8 + 4 + 2 + 0 + 1 = 15. By adding 0 to the number 15, it becomes 15. The number 15 is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 0. Hence, 842001 is the required digit of a given number.
(iv) 749_262 The given number is 749_262. Add the digits of the given number. Add 7, 4, 9, 2, 6, and 2. 7 + 4 + 9 + 2 + 6 + 2 = 30. By adding 0 to the number 30, it becomes 30. The number 30is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 0.
Hence, 7490262 is the required digit of a given number.
(v) 998_32 The given number is 998_32. Add the digits of the given number. Add 9, 9, 8, 3, and 2. 9 + 9 + 8 + 3 + 2 = 31. By adding 2 to the number 31, it becomes 33. The number 33 is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 2.
Hence, 998232 is the required digit of a given number.
(vi) 1_7072 The given number is 1_7072. Add the digits of the given number. Add 1, 7, 0, 7, and 2. 1 + 7 + 0 + 7 + 2 = 17. By adding 1 to the number 17, it becomes 18. The number 18 is divisible by 3. The lowest possible digit in the blank space to make the number divisible by 3 is 1. Hence, 117072 is the required digit of a given number.
See More Divisibility Tests:
Leave a Comment Cancel Reply
You must be logged in to post a comment.
Divisibility rule
A divisibility rule, also referred to as a divisibility test, is a rule that can be used to determine whether one number is divisible by another. Generally, a number is divisible by another if the quotient is a whole number (i.e. there is no remainder).
There are also divisibility rules for testing whether a given number is divisible by specific integers. The divisibility rules for the integers 1-10 are included below. Divisibility rules exist for other integers as well, but in some cases, applying the divisibility rule may be more tedious than just performing the division problem to see if the remainder is 0.
Divisibility by 1
All numbers are divisible by 1. No matter what the number is, dividing it by 1 will result in the same number.
Divisibility by 2
If a number has an even number (0, 2, 4, 6, 8) in the ones place, 2 divides the number. For example, 2 divides 3,018 because 8 is an even number.
Divisibility by 3
If 3 divides the sum of the digits of a number, 3 divides the number. For example, 3 divides 2,310 because the sum of 2, 3, 1, and 0 is 6, and 3 divides 6.
Divisibility by 4
If 4 divides the last two digits of a number, 4 divides the number. For example, 4 divides 8,728 because 4 divides 28.
Divisibility by 5
If a number has a 0 or a 5 in the ones place, 5 divides the number. For example, 5 divides both 385 and 400.
Divisibility by 6
If both 2 and 3 divide a number, 6 also divides that number. For example, 6 divides 396 because both 2 and 3 divide 396.
Divisibility by 7
If the result of subtracting two times the last digit in a number from the rest of the number, excluding the last digit, is divisible by 7, then the original number is divisible by 7. Using 7,196 as an example:
6 × 2 = 12
719 - 12 = 707
707 ÷ 7 = 101
Since 7 evenly divides 707, 7,196 is divisible by 7.
Divisibility by 8
If the last 3 digits in a number are 0, the number is divisible by 8. If the last 3 digits are not 0, but the number formed by the last 3 digits of the original number is divisible by 8, then the original number is divisible by 8.
Using 50,496 as an example:
496 ÷ 8 = 62
Since 496 is divisible by 8, 50,496 is divisible by 8.
Divisibility by 9
If 9 divides the sum of the digits of a number, 9 divides the number. For example, 9 divides 198,432 because 1 + 9 + 8 + 4 + 3 + 2 = 27, and 9 divides 27, so 9 divides 198,432.
Divisibility by 10
If the last digit of a number is 0, then the number is divisible by 10. For example, 10 evenly divides 710.
Divisibility Test Calculator
What are divisibility tests, how to use this divisibility test calculator, divisibility tests of 2, 4, and 8, divisibility tests of 3 and 9, divisibility tests of 5 and 25, divisibility tests of 10, 100, etc., divisibility test of 7, divisibility test of 11, divisibility test of 13, other divisibility tests.
If you have ever struggled with testing for divisibility, rest assured that these times are gone for good: we present Omni's divisibility test calculator, the ultimate tool on your journey to master divisibility tests once and for all!
While scrolling down to a short article below, you will get a chance to:
- Learn what divisibility tests are;
- Get tips on how to most efficiently use this divisibility test calculator; and
- Those that are the simplest and most useful in real life, like the divisibility test of 2 or 10;
- Those that are most widespread in schools, like the divisibility test of 3, 9, or 11; and
- Those that are a bit more complicated and seldom even mentioned, so useful when you want to, e.g., impress your teacher, like the divisibility test of 7 or 13.
Let us first recall what "divisibility" means. We say that a natural number n is divisible by another natural number k if dividing n / k leaves no remainder (i.e., the remainder is equal to zero).
Example: 18 is divisible by 3 because 18 / 3 = 6 and there is no remainder. 18 is also divisible by 6 , by 2 , and by 9 — but not by 7 , as 18 / 7 = 2.57 .
Don't hesitate to visit our remainder calculator if you feel you need to refresh your knowledge.
Now we move on to divisibility rules . These are mathematical procedures, recipes, and tricks that allow us to quickly and easily determine if a given number n is divisible by some specific divisor k but without performing the actual division , which is very useful if the number we need to examine is very large and long division would take us veeeery long. However, if you wanna try, here's the link to Omni's long division calculator .
Usually, a divisibility rule tells us how to replace our problem with an easier problem — that is, transform n into a smaller number. The strategies include:
- Looking only at the last digit and ignoring the rest (e.g., the divisibility test for 2);
- Looking only at several last digits and ignoring the rest (e.g., the divisibility test for 4);
- Computing the sum of digits of a number (e.g., the divisibility test of 9);
- Computing the alternating sum of digits of a number (e.g., the divisibility test of 11);
- Computing the sum of blocks of digits of a number (e.g., another divisibility test for 11); and
- Computing the alternating sum of blocks of digits of a number (e.g., the divisibility test of 13).
We then check the desired divisibility for this smaller number, which is much easier in principle. If it is still hard, you can often apply the divisibility test again , leading to a yet smaller number, for which the solution to the divisibility question should be clear.
In what follows, we first explain how our divisibility test calculator works. Next, we will lead you through all the most useful divisibility tests.
Our divisibility test calculator has two modes : Details and Summary .
In the Summary mode, you can overview the divisibility properties of a given integer: the calculator will tell you which numbers between 2 and 13 are its divisors.
In the Details mode, you can understand why a number between 2 and 13 is (or is not) a divisor of a given integer. The calculator will display the appropriate divisibility rule and will show you how to apply it.
In general, to test divisibility by any natural number of the form 2ⁿ , we only have to examine its last n digits and check if they form a number that is divisible by 2ⁿ . In particular:
Divisibility test of 2
A number is divisible by 2 if and only if its last digit is even , i.e., divisible by 2. In other words, the last digit must be equal to 0, 2, 4, 6, or 8.
Divisibility test of 4
A number is divisible by 4 if and only if its last two digits form a number divisible by 4, i.e., they are equal to any of the following numbers: 00, 04, 08, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, or 96.
Divisibility test of 8
A number is divisible by 8 if and only if its last three digits form a number divisible by 8.
As you can see, already for 8 this rules is not very practical — deciding on the fly if a given three-digit number is divisible by 8 may be hard. Fortunately, there's another divisibility rule for 8, which involves examining separately the hundreds digit and the last two digits.
Alternative divisibility test of 8
If its hundreds (third-last) digit is even , a number is divisible by 8 if and only if the number formed by the last two digits is divisible by 8.
If its hundreds digit is odd , a number is divisible by 8 if and only if the number formed by the last two digits plus 4 is divisible by 8.
These next two divisibility tests are very popular among math teachers, they love talking about them. Learn them to be prepared!
Divisibility test of 3
A number is divisible by 3 if and only if the sum of its digits is divisible by 3.
Divisibility test of 9
A number is divisible by 9 if and only if the sum of its digits is divisible by 9.
How do I prove the divisibility rules for 3 and 9?
The two rules above seem non-obvious and maybe even impossible, but in fact, it is quite easy to prove them ! Let's consider a natural number n which has five digits: a , b , c , d , e (when looking from left to right).
Since we use the positional system with base 10, we can rewrite this number as
n = 10000a + 1000b + 100c + 10d + e
Let's perform a simple trick:
n = 9999a + 999b + 99c + 9d + (a + b + c + d + e)
Now we see that
n - (a + b + c + d + e) = 9999a + 999b + 99c + 9d
n - (a + b + c + d + e) = 9 × (1111a + 111b + 11c + d)
We now stop the calculations and think for a moment.
The right-hand side is clearly divisible by both 3 and 9, because of the 9 at the start. This means our left-hand side (which is the difference between our initial number n and the sum of its digits) is also divisible by both 3 and 9. Because of that, we can say that both n and (a + b + c + d + e) have the same remainder when divided by 3 or by 9 . We can then check the remainder of n/3 by checking (a + b + c + d + e) / 3 's remainder (and the same for 9 ), which would be a much easier calculation.
Therefore, n itself is divisible by 3 if and only if the sum of its digits is divisible by 3 . In the same way, n is only divisible by 9 if its digits' sum is 9 . And this is exactly what we wanted to prove!
To test the divisibility of n by 5ᵏ , we only need to examine the divisibility of the last k digits of n by 5ᵏ .
Divisibility test of 5
A number is divisible by 5 if and only if its last digit is 0 or 5.
Divisibility test of 25
A number is divisible by 25 if and only if its last two digits form a multiple of 25, i.e., they are one of the following: 00, 25, 50, or 75.
These rules are very simple and similar to what we've seen with 5 and 25: for divisibility by powers of 10, we need as many zeroes at the end of our number as there are zeros in the divisor:
A number is divisible by 10 if and only if its last digit is 0.
A number is divisible by 100 if and only if its last two digits are 00.
A number is divisible by 10ⁿ if and only if its last n digits are all zeros.
A number is divisible by 7 if and only if subtracting two times the last digit from the rest gives a number divisible by 7.
Don't hesitate to use Omni's divisibility test calculator to generate examples and see how this rule works in practice!
In fact, there are several popular divisibility tests for 7 — let's take at look at two more:
Alternative rule for divisibility by 7
A number is divisible by 7 if and only if subtracting nine times the last digit from the rest gives a number divisible by 7.
Yet another alternative rule for divisibility by 7
A number is divisible by 7 if and only if the alternating sum of blocks of three digits from right to left is divisible by 7.
🙋 Computing the alternating sum of some numbers means that we have to alternate sign . That is, we start with addition, which is followed by subtraction, then by addition again, etc. For example, the alternating sum of the digits of 918,273,645 is 9-1+8-2+7-3+6-4+5 = 25 .
A number is divisible by 11 if and only if the alternating sum of its digits is divisible by 11 .
🙋 The alternating sum of digits may yield a negative number . Fear not — you can simply ignore the minus sign. For instance, if the alternating sum equals -55, then we can simply observe that 55 is divisible by 11, and so your initial number is also divisible by 11.
There's yet another divisibility test for 11, where we do not have to perform an alternating sum but a normal one. However, we have to take blocks of two digits:
Alternative rule for divisibility by 11
A number is divisible by 11 if and only if adding its digits in blocks of two from right to left we get a number divisible by 11.
A number is divisible by 13 if and only if the alternating sum of blocks of three digits from right to left is divisible by 13.
For instance, if you deal with n = 9,111,414 , you calculate 414 − 111 + 9 = 312 . Since 312 is divisible by 13 (because 312 / 24 = 13 ), we conclude that 9,111,414 is divisible by 13 as well.
To see more examples, use our divisibility test calculator!
It is simple to derive divisibility tests for non-prime divisors using prime factorization. Namely, consider the divisor of the form:
k = pᵃ × qᵇ × ... × rᶜ ,
- p , q , and r are prime numbers ; and
- a , b , and c are the prime number's powers in this factorization. Visit the prime factorization calculator if you need more details.
To find out if a given number n is divisible by this k , we need to test its divisibility by all prime numbers raised to their respective powers in the factorization, i.e., by pᵃ , by qᵇ , etc.
Let's look at some examples of k , how each k is factorized into prime-power pairs, and how that determines the divisibility rule for k :
A number is divisible by 6 = 2 × 3 if and only if it is divisible by 2 and by 3.
A number is divisible by 12 = 2² × 3 if and only if it is divisible by 4 and by 3.
A number is divisible by 15 = 3 × 5 if and only if it is divisible by 3 and 5.
A number is divisible by 18 = 2 × 3² if and only if it is divisible by 2 and 9.
A number is divisible by 20 = 2² × 5 if and only if it is divisible by 4 and by 5.
Simple — automatic even — but less and less useful, right? However, sometimes we can rephrase these rules into slightly more useful counterparts. Let's see how we rephrase the last rule from simply "divisible by 20 means divisible by 4 and by 5":
"A number is divisible by 20 if and only if the second-last digit is even and the last digit is 0."
How do we prove this reworded rule? It's easy! Let's take a look.
Since our number must be divisible by 5 (the first requirement from our original divisible-by-20 rule), we remember its last digit must be 0 or 5. But if it were 5, then there would be no chance for the divisibility by 2, and thus by 4 (which is the second requirement). Hence, the last digit must be 0.
And now, we recall the divisibility rule for 4: the last two digits must form a number that is divisible by 4. So far, we've established that the last digit must be zero, and so the last two digits are allowed to be any of 00, 10, 20, 30, 40, 50, 60, 70, 80 , and 90 . Those among them that are divisible by 4 are 00, 20, 40, 60 , and 80 . What do they have in common? Their first digit is even, exactly as we claimed with our rephrased rule.
What is a divisibility test?
A divisibility test is a mathematical procedure that allows you to quickly determine whether a given number is divisible by some divisor. Either we can completely avoid the need for the long division or at least end up performing a much simpler one (i.e., for smaller numbers).
How do I test divisibility by 7?
To check if a number is divisible by 7, follow these steps:
Divide your number into blocks of three digits from right to left.
Compute the alternating sum of these blocks , from right to left.
Checks if the result is divisible by 7. If it is, then your number is divisible by 7 too. If not, then your number is not divisible by 7.
If the result to be examined is very large, then repeat Steps 1 and 2 with this new number.
How do I test divisibility by 11?
We check if a number is divisible by 11 as follows:
Compute the alternating sum of digits .
Checks if the result is divisible by 11. If it is, then so is your number. If not, then your number is not divisible by 11.
If the result to be examined is very large, repeat Steps 1 and 2 with this new number.
Alternatively, you can replace Step 1 as follows: Divide your number into blocks of two digits from right to left, then compute the sum of these blocks .
Is 1111 divisible by 11?
Yes, 1111 is divisible by 11 . To verify this claim, compute the alternating sum of digits and check if it is divisible by 11: 1 − 1 + 1 − 1 = 0 . Of course, 0 is divisible by 11 (and by any other number), and so 1111 is divisible by 11.
Is 111 divisible by 11?
No, 111 is not divisible by 11 . Computing the alternating sum of digits we get: 1 − 1 + 1 = 1 . And of course, 1 is not divisible by 11.
Average percentage
Height of a cylinder.
- Biology (103)
- Chemistry (101)
- Construction (148)
- Conversion (304)
- Ecology (32)
- Everyday life (263)
- Finance (592)
- Health (443)
- Physics (513)
- Sports (108)
- Statistics (184)
- Other (186)
- Discover Omni (40)

Numbers & Quantities

Statistics & Probability

More Learning Tools
Encyclopedia
Pen & Paper exercises
Excel / GeoGebra recipes
Tutor-on-Demand
Junior Math
Multiplication Master
Treasure Trail
Wind Surfer
Stack n´load
Language: English
Divisibility Rules
What is the divisibility rule for 4.
A number is divisible by 4 if the number formed by its last two digits is divisible by 4. This video explains the process through the use of examples.
Divisibility Rules: Dividing by 3
Help math learners review the divisibility rule for 3 with this fun practice worksheet! Geared toward third- and fourth-grade students, this worksheet begins with a review of the rule that states that a number is divisible by 3 if the sum of its digits is divisible by 3. Learners will also be shown an example and a non-example of this divisibility rule. Then, students will be asked to apply the rule to a set of given numbers, ranging from two digits to five digits, circling all the numbers that are divisible by 3. Learning divisibility rules is a great way to help learners build number sense and confidence when working with larger numbers. Next up, check out the Divisibility Rules: Dividing by 4 worksheet!
View aligned standards
Related guided lesson.

Multiplication and Division

Divisibility Calculator
Enter any 2 numbers to see how the divisibility rules explain things
Worksheet on Divisibility Rules Divisibility Rules Lesson Divisibility quiz
Check if any two numbers are divisible by using the calculator below. Just fill in the numbers and let us do the rest.
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

Lesson Streak

Learn Spelling
Learn grammar, learn handwriting.

Get the Reddit app
What the title says :3 (I’m still active) - Dm me if you got an error and need help with it * Raging2Raven * for replit - posts will be made as soon as I solve the practice - help is encouraged, up to you - Replit is used to prevent Reddit from mangling the code - this subreddit is made to give you an “idea” on how to finish the practice
Assignment 4: divisible by three
Sorry for the delayed posting, I like just got dumped last night soooo yeah
By continuing, you agree to our User Agreement and acknowledge that you understand the Privacy Policy .
Enter the 6-digit code from your authenticator app
You’ve set up two-factor authentication for this account.
Enter a 6-digit backup code
Create your username and password.
Reddit is anonymous, so your username is what you’ll go by here. Choose wisely—because once you get a name, you can’t change it.
Reset your password
Enter your email address or username and we’ll send you a link to reset your password
Check your inbox
An email with a link to reset your password was sent to the email address associated with your account
Choose a Reddit account to continue

IMAGES
COMMENTS
To write a program using a loop in Python, you can leverage the language's high-level and readable design.Python's emphasis on code readability is evident through its use of indentation.. How to explain. It supports multiple programming paradigms, including functional, object-oriented, and structured programming.. One common type of loop in Python is the while loop, which allows you to execute ...
A whole number is said to be divisible by 3 if the sum of all digits of that whole number is a multiple of 3 or exactly divisible by 3.. Divisibility Rule of 3 with Examples. The divisibility rule for 3 can be understood with the help of the following examples.. Example: Test the divisibility of the following numbers by 3. a.) 1377. b.) 2130. c.) 3194. Solution: a) In 1377, the sum of all the ...
A number is divisible by 12 if the number is divisible by both 3 and 4. Is 180 is divisible 12? 180 is divisible by 3 since 1 + 8 + 0 = 9 and 9 is divisible 3. 180 is divisible by 4 since 80 is divisible by 4. Therefore, 180 is divisible by 12. Rule # 12: divisibility by 13. Add four times of the last digit of the number to the remaining number.
Here, as 12 is divisible by 3, 93 is also divisible by 3. Example 2: 45,609. To make the process even easier, you can also find the sum of the digits until you get a single digit. Sum of digits = 4 + 5 + 6 + 9 + 0 = 24. Adding further, we get 2 + 4 = 6. 6 is divisible by 3. Thus, 45609 is divisible by 3. Divisibility Rule of 4
From the divisibility rules, we know that a number is divisible by 12 if it is divisible by both 3 and 4. Therefore, we just need to check that 1,481,481,468 is divisible by 3 and 4. Applying the divisibility test for 3, we get that \ (1+4+8+1+4+8+1+4+6+8=45,\) which is divisible by 3. Hence 1,481,481,468 is divisible by 3.
Or use the "3" rule: 7+2+3=12, and 12 ÷ 3 = 4 exactly Yes. Note: Zero is divisible by any number (except by itself), so gets a "yes" to all these tests. Any integer (not a fraction) is divisible by 1. The last digit is even (0,2,4,6,8) The sum of the digits is divisible by 3. This rule can be repeated when needed:
Lessons with videos, examples, solutions and stories to help students learn the Divisibility Rules. The multiple of a number is always divisible by the number. The word "divisible" means that it can be divided exactly. 144 ÷ 4 = 36 (remainder = 0). So, 144 is divisible by 4 and is a multiple of 4. 144 ÷ 5 = 28 (remainder = 4).
This can be justified by the divisibility rule of 3. So, the number 81 is divisible by 3. The divisibility rule of 3 states that if the sum of digits of a number is a multiple of 3 or divisible by 3, the number will be divisible by 3. Get the proof for the divisibility rule of 3, along with examples, here at BYJU'S.
Divisibility Rules for some Selected Integers. Divisibility by 1: Every number is divisible by \ (1\). Divisibility by 2: The number should have \ (0, \ 2, \ 4, \ 6,\) or \ (8\) as the units digit. Divisibility by 3: The sum of digits of the number must be divisible by \ (3\). Divisibility by 4: The number formed by the tens and units digit of ...
What Is the Divisibility Rule for 3? A number is divisible by 3 if the sum of its digits is divisible by 3. This video explains why this is, and demonstrates how to use the rule, with examples. The media could not be loaded, either because the server or network failed or because the format is not supported. Tip: If you know the content of the ...
The lowest possible digit in the blank space to make the number divisible by 3 is 1. Hence, 201987 is the required digit of a given number. (iii) 8420_1. The given number is 8420_1. Add the digits of the given number. Add 8, 4, 2, 0, and 1. 8 + 4 + 2 + 0 + 1 = 15. By adding 0 to the number 15, it becomes 15.
Since 7 evenly divides 707, 7,196 is divisible by 7. Divisibility by 8. If the last 3 digits in a number are 0, the number is divisible by 8. If the last 3 digits are not 0, but the number formed by the last 3 digits of the original number is divisible by 8, then the original number is divisible by 8. Using 50,496 as an example: 496 ÷ 8 = 62
In general, to test divisibility by any natural number of the form 2ⁿ, we only have to examine its last n digits and check if they form a number that is divisible by 2ⁿ.In particular: Divisibility test of 2. A number is divisible by 2 if and only if its last digit is even, i.e., divisible by 2.In other words, the last digit must be equal to 0, 2, 4, 6, or 8.
What Is the Divisibility Rule for 4? A number is divisible by 4 if the number formed by its last two digits is divisible by 4. This video explains the process through the use of examples. The media could not be loaded, either because the server or network failed or because the format is not supported. Tip: If you know the content of the video ...
Geared toward third- and fourth-grade students, this worksheet begins with a review of the rule that states that a number is divisible by 3 if the sum of its digits is divisible by 3. Learners will also be shown an example and a non-example of this divisibility rule. Then, students will be asked to apply the rule to a set of given numbers ...
3 - The sum of the digits is a multiple of 3 (3654…3 + 6 + 5 + 4 = 18 (18 ÷ 3 = 6)) 4 - The last two digits are a multiple of 4 (12364….64 ÷ 4=16) 5 - The last digit will be 0 or 5 6 - The number is divisible by BOTH 2 & 3 8 - The last three digits are divisible by 8 10 -The last digit will be 0 12 - The number is divisible by BOTH 3 & 4 ...
Table 5.3.1: Divisibility Rules; Divisible by ___? The Trick! 2. Last digit is even. 3. Add up the digits and if the sum is divisible by 3 then so is the original number. 4. Divide last 2 digits by 4. 5. Ends in 0 or 5. 6. Rules for 2 and 3 work. 8. Divide last 3 digits by 8. 9. Add up the digits and if the sum is divisible by 9 then so is the ...
Since the last two digits, 12, are divisible by 4, the number 112 is also divisible by 4. 10,948: The last two digits, 48, are divisible by 4. Therefore, the whole number is also. 100,002,088: Yep, this satisfies rule because 88 is divisible by 4!-12,036: 36 and 36 is evenly divided by 4, so -12,036 passes the test!
Check if any two numbers are divisible by using the calculator below. Just fill in the numbers and let us do the rest. Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there! Interactive simulation the most controversial math riddle ever! Divisibility rules calculator for divisibility by 2,3,4,5,6,8,9,10, and 11.
Let's find the sum of the digits: 4 + 5 + 5 + 4 = 18. Add the digits once more. 1 + 8 = 9. The sum of the digits is 9. 9 is divisible by 3. So yes, 4,554 is divisible by 3. . Since 4,554 is divisible by both 2 and 3, this means it's divisible by 6. 👍.
The program starts by asking the user for the total number of checks. It then enters a for loop where it prompts the user to input a number and checks if it's divisible by 3 using the modulus operator. The program keeps count of how many numbers are divisible and how many are not. After the loop, it prints the counts. profile. Nice explanation ...
Divisibility by three is a basic concept in arithmetic that is important to understand for various mathematical operations.. In order to determine if a number is divisible by three, you can use the rule of threes: add up the digits of the number and if the sum is divisible by three, then the original number is also divisible by three.For example, let's consider the number 453.
Assignment 4: divisible by three unit 4 Sorry for the delayed posting, I like just got dumped last night soooo yeah Share Add a Comment. Be the first to comment Nobody's responded to this post yet. Add your thoughts and get the conversation going. Top 69% ...