percentages as decimals problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Multiplying and dividing 10, 100, 1000

Percent to decimal

Here you will learn about converting percents to decimals.

Students will first learn about converting percents to decimals in 6th grade math as part of their work with ratios and proportional relationships and will expand that knowledge to solving problems such as finding the whole given a part and the percent or finding the part given the whole and the percent.

This will later be used to find percent increase/decrease in 7th grade.

What is percent to decimal?

Converting a percent to a decimal is representing the percentage as a decimal without changing its value.

The word “percent” means one part out of one hundred, and you can use this information to express a percent as a decimal.

For example,

\begin{aligned} &25\%=0.25\\\\ &45 \%=0.45\\\\ &33.3 \%=0.33333...\\\\ &80 \%=0.8 \end{aligned}

Common Core State Standards

How does this apply to 6th grade math?

Grade 6 – Ratios and Proportional Relationships (6.RP.A.3a) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.

How to convert percentages to decimals

In order to convert from a percent to a number in its decimal form, you need to:

Divide the percent by \bf{100} .

Clearly state the answer showing ‘percent’ = ‘decimal’.

[FREE] Converting Fractions, Decimals and Percents Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of converting fractions, decimals and percents. 10+ questions with answers covering a range of 4th, 5th and 6th grade converting fractions, decimals and percents topics to identify areas of strength and support!

Percent to decimal examples

Example 1: converting a simple percentage to a decimal..

Convert 60\% to a decimal.

You know that the percent sign (\%) means the number is out of 100.

Therefore, if you divide the number (without the percent symbol) by one hundred, you will have the equivalent decimal without having changed its value.

60\% = 60\div100=0.6

If you are not sure how to divide a number by 100, review place value and/or dividing by powers of 10. A summary of the process is below for this example.

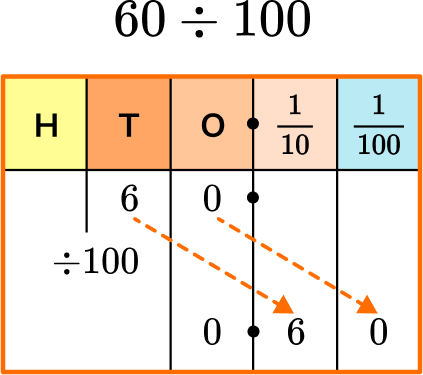
When you divide by 100, you move the digits two places to the right. The decimal point does not move.

Here you can see that the 6 has moved from the tens place to the tenths place in the first decimal place.

You can see that the 0 has moved from the ones place to the hundredths place in the second decimal place.

60\div100=0.60=0.6

2 Clearly state the answer showing ‘percent’ = ‘decimal’.

Example 2: converting a percentage to a decimal

Convert 8\% to a decimal.

8\% = 8\div100=0.08

Example 3: converting a percentage (involving a decimal) to a decimal

Convert 52.3\% to a decimal.

52.3\% = 52.3\div100=0.523

52.3\% = 0.523

Example 4: converting a percentage (involving a repeating decimal) to a decimal

Convert 4.\overline{2}\% to a decimal.

4.\overline{2}\%=4.\overline{2} \div 100

Note: Remember the 2 is a repeating decimal. It will still be repeating indefinitely after being divided by 100.

0.\overline{2} \div 100=0.00 \overline{2}

4.\overline{2}\%=4.\overline{2} \div 100=0.04 \overline{2}

4.\overline{2} \%=0.04 \overline{2}

Example 5: converting a percentage (above 100 ) to a decimal

Convert 145.1\% to a decimal.

145.1\% = 145.1\div100=1.451

145.1\% = 1.451

Example 6: converting a percentage to a decimal

Convert 102.04\% to a decimal.

102.04\% = 102.04\div100=1.0204

102.04\% = 1.0204

Teaching tips for percent to decimal

Use visual models such as hundreds grids or pie charts to illustrate the equivalence of percents and decimals and to demonstrate how both forms are ways to represent a part of a whole or a rate.
Use real world contexts to demonstrate how percentages can be thought of as decimals.
Conversion table worksheets for percent to decimal conversion have their place, but make sure that students have a conceptual understanding of the relationship between percentages and decimals.

Easy mistakes to make

Dividing incorrectly by \bf{100} Often mistakes are made when dividing by 100. The common mistakes are: ◌ Dividing by 10 instead of 100. ◌ Multiplying instead of dividing. ◌ Mistakes with decimals. Make sure you are confident with the below equations: Example, 4 \div 100=0.04 0.4 \div 100=0.004 0.04 \div 100=0.0004
Not including repeating decimals in the percentages You need to remember to take the repeating decimal into account when dividing by a power of 10. Example, 0.\overline{4} \div 10=0.0\overline{4} not 0.04

Related lessons on converting fractions, decimals, and percentages

Fraction to percent
Percent to fraction
Decimal to percent
Decimal to fraction
Fraction to decimal
Repeating decimal to fraction

Practice percent to decimal questions

1. Convert 25\% to a decimal.

Start by dividing the percent value by 100.

25 \div 100

This gives you 0.25.

2. Convert 87.5 \% to a decimal.

87.5 \div 100

This gives you 0.875.

3. Convert 175\% to a decimal.

175 \div 100

This gives you 1.75.

4. Convert 760\% to a decimal.

760 \div 100

This gives you 7.6.

5. Convert 44.\overline{4} \% to a decimal.

44 . \overline{4} \div 100

This moves the whole number digits in 44 two place value spaces to the right, placing them behind the decimal.

Because this is a repeating decimal with the digit 4 repeating, and now you have moved the 4’ s in the whole number behind the decimal, this means you have all 4’ s behind the decimal, repeating infinitely.

This gives you 0 . \overline{4}.

6. Convert 18.\overline{18} \% to a decimal.

18 . \overline{18} \div 100

This moves the whole number digits in 18 two place value spaces to the right, placing them behind the decimal.

Because this is a repeating decimal with the digits 18 repeating, and now you have moved the 18’ s in the whole number behind the decimal, this means you have all 18’ s behind the decimal, repeating infinitely.

This gives you 0 . \overline{18}.

Percent to decimal FAQs

You only write the repeating sequence once. If the decimal value that is repeating is all the same digit, you can just use one digit behind the decimal with a bar over the digit. If the repeating decimal is a sequence of three digits before repeating again, you would write the three digits with a bar over all of them.

Multiples of 10 are the products of 10 with any other integer. Powers of 10 are also multiples of 10, but more specifically the multiples that can be expressed as 10 to the power of another number, indicating the number of times you multiply 10 by itself.

If your percentage is greater than 100\%, your decimal equivalent will be greater than 1. If your percentage is less than 100\%, your decimal equivalent will be less than 1. If your percentage is equal to 100\%, your decimal equivalent will be equal to 1.

The next lessons are

Compound measures
Properties of equality

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.