lesson 5 problem solving practice fundamental counting principle

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Fundamental counting principle – Explanation & Examples

JUMP TO TOPIC

Fundamental Counting Principle definition

Fundamental counting principle formula, practice question:, fundamental counting principle – explanation & examples.

The fundamental counting principle is a mathematical rule that is extensively applied in the evaluation total number of possible arrangements of a set of objects. These calculations are essential for solving many probability problems.

The fundamental counting principle states that if one event can occur in $A$ different ways and a second event can occur in $B$ different ways, then the total number of ways in which both events can occur is $A \times B$.

After reading this article, you should understand:

• The Fundamental Counting Principle
• Difference Between the Rule of Sum and the Counting principle
• Examples of the Fundamental Counting Principle
• Applications of the Counting principle   

It is advisable to refresh the set theory to better understand the material discussed in this article.                                                        

What is the Fundamental Counting Principle

Let us consider the example of flipping a fair coin twice. When the coin is tossed the first time, we either get Heads or Tails, and the sample space can be written as $S = \{H, T\}$. When the coin is tossed the second time, the sample space we get is $S = \{HH, HT, TH, TT\}$. The first flip can result in two different outcomes, and so does the second flip. So, the total number of possible outcomes is $2 \times 2 =4$. The example is illustrated in the form of a tree diagram below:    

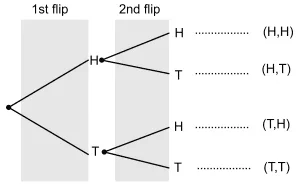
Let us take another simple example, James has to go to a party, and he has three different shirts and two different pants to choose from. The shirts are red, black and white in color while the pants are blue and green in color. How many possible outfits can James choose from? James can wear either of the two pants with each shirt.

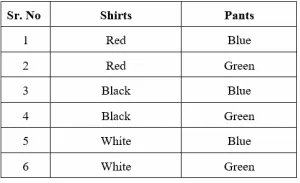
So, James can wear Red shirt with either Blue or Green pants. Similarly, Black and White shirts can be selected with either Blue or Green pants. As the table shows, there are six numbers of possible outfits. We can calculate it easily through the rule of counting principle. We had 3 different options for shirts and two different options for pants so, $3 \times 2=6$ possible outfits.

If there are $A$ different ways of selecting an object and $B$ different ways of selecting another object, then the total number of possible ways for selecting both objects together is $A\times B$.  

Example 1 : Harry went to a food restaurant, and he wants to order a combo deal that includes a pizza, drink, and dessert. The following choices are available:

Pizza : Chicken Fajita and Vegetable

Drink : Pepsi and 7-Up

Dessert : Ice-cream and Pie

We are given three different objects to choose from. There are three different types of pizza, four different types of drinks, and three different types of dessert. Let us draw a tree diagram.

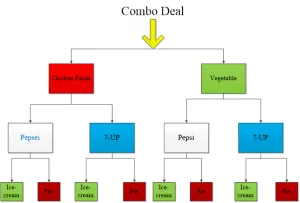
As the tree diagram shows, we can work out the possible arrangements for a combo deal.

Deal 1: Chicken fajita, Pepsi, and Ice-cream

Deal 2: Chicken fajita, Pepsi, and Pie

Deal 3: Chicken fajita, 7-UP, and Ice-cream

Deal 4: Chicken fajita, 7-UP, and Pie

Deal 5: Vegetable Pizza, Pepsi, and Ice-cream

Deal 6: Vegetable Pizza, Pepsi, and Pie

Deal 7: Vegetable Pizza, 7-UP and Ice-cream

Deal 8: Vegetable Pizza, 7-UP and Pie

Now solving it by counting principle, we have 2 options for pizza, 2 for drinks and 2 for desserts so, the total number of possible combo deals $= 2 \times 2 \times 2 =8$.

  Example 2 : Steve has to dress for a presentation. He has $3$ different shirts,$ 2$ different pants, and$ 3 $ different shoes available in his closet. Wearing the Tie is optional. Calculate the total number of possible outfits. 

There are three types of shirts, two types of pants and three types of shoes. While the tie is optional, the tie has two options, either “Yes” or “No.”

Total number of possible outfits $ = 3 \times 2 \times 3 \times 2= 36$.

  The Rule of Sum

The rule of sum states that if event $A$ can occur in $n$ different ways and event $B$ can occur in $m$ different ways. In contrast, both events $A$ and $B$ are mutually exclusive , then the total number of possible outcomes can be given as $n + m$. So, unlike the counting principle, we add both the events; however, it must be remembered that the condition for the rule of the sum is that the events must be mutually exclusive.         

Example 3 : Jessica has a jar of cookies. It has $3$ chocolate and $3$ peanut cookies in it. Jessica only wants to eat one cookie. How many possible options does Jessica have?

Since Jessica only wants one cookie, she has to choose only one cookie from 3 chocolate or 3 peanut cookies. The choices are mutually exclusives, so by applying the rule of sum, we have $3+3= 6$ possible options.

Example 4 : Ellie went to a dress shop to purchase a single blue dress. The shop has $14$ plain blue dresses, $13$ plain red dresses, 10 blue embroidered dresses, and $5$ red embroidered dresses. How many options does Ellie have?

Since Ellie wants to choose a blue dress so, we will eliminate all red dresses. She can choose from 14 plain blue dresses or 10 blue embroidered dresses. So, the total numbers of option are $14+10 = 24$

  The Counting Principle and Rule of Sum

We have discussed the problems related to the fundamental counting principle and the rule of sum. What if a problem has to be solved using both the rules? Let us discuss a few examples.

  Example 5 : Harris went to a shop to buy some items of clothing. He can choose a shirt from 3 different colors or a T-shirt from 2 different colors. Also, he can either get a pair of pants from 3 available colors or a pair of jeans from three available colors. How many possible outfits can Harris have?    

Harris can take one shirt from the given 3 colors or T-shirts from the available 2 colors. So number of available shirts $= 3+2 =5$.

Similarly, he can choose a pair of pants from either 3 options or a pair of jeans from three options. The number of available pairs of jeans/pants $3+3=6$.

So, we have $5$ different shirts and $6$ different pants, and the total number of possible outfits will be $5 \times 6= 30$.

Example 6 : Steve wants to go to a job interview in another city. He can choose from $4$ local bus services or $3$ taxi services to reach the other city. From there, he can choose from $3$ local bus services or $2$ taxi services to reach the place of his interview. How many possible routes/ways Steve can travel to his destination?  

Steve can choose to take either a local bus or a taxi to reach the other city. So, the possible numbers of vehicles that can be used to reach the city are $4+3 =7$. Similarly, Steve can either choose from $3$ local bus services or $2$ taxi services to reach the location of the interview from the city. Number of possible option $3+2=5$. Now, the total number of ways/vehicles Steve can use to reach his interview destination is $7 \times 5 = 35$.  

The basic formula for the fundamental counting principle is the same as its definition, i.e., if we have $A$ ways/options to do task-1 and $B$ ways to do task-2, then the total number of ways we can do task-1 and task-2 together are $A \times B$.

However, by applying the fundamental counting principle in questions related to possible arrangements of a given set of objects, we can derive formulae for permutations and combinations as discussed below:

Applications of the Counting Principle

Suppose $5$ boys $\textrm{A, B, C, D, and E}$ are to be seated on a couch in a row. Then in how many possible ways can they be seated? Suppose that $\textrm{Boy A} = \textrm{event A}$, $\textrm{Boy B} = \textrm{event B}$ and so on. So, for event $A$, we have five possible options, for the event $B$, we have four possible options, for the event $C$, we have three possible options, for the event $D$, we have two possible options and one option for the event $E$.

By the rule of counting principle to calculate the total number of ways, we multiply the possibilities of each event. In this case the total number of possible outcomes is $5 \times 4 \times 3 \times 2 \times 1= 120$. This is also known as permutation, and it is an application of the counting principle.  

Permutation

A permutation of $n$ different objects taken $r$ at a time where $r ≤ n$, then the arrangement of r objects can be represented by

$  P(n,r) = \frac{n!}{(n-r)!} $

Where $n! = n\times(n-1)\times(n-2)…..\times1$.

Example 7 : Calculate the number of ways in which digits from $0-9$ can be arranged.  

There are total numbers of $10$ digits. The number of ways in which the first digits can be arranged is 10. Similarly, for the second digit, we have 9 available options and so on for the rest of the digits. The total numbers of possible ways to arrange the digits

$10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800$.  

Example 8 : Calculate the number of ways in which four digits can be selected from $0-9$.

There are total numbers of 10 digits, and we have to select only four from the available 10 digits. Here $n = 10$ while $r = 4$.

                                    $  P(n,r) = \frac{n!}{(n-r)!} $

                                    $  P(n,r) = \frac{10!}{(10-4)!} $

                                    $  P(n,r) = \frac{10!}{6!} $

                                    $  P(n,r) = \frac{2628800}{720} $

                                    $  P(n,r) = 5040 $.  

Just Like permutation, the combination is also an application of the counting principle.

Combination

The combination is a process of selecting objects from a set without giving importance to the order of arrangement. For instance, let’s suppose we have a class of four students; let’s call them $A$, $B$, $C$, and $D$. We wish to make a team of three students. How many different teams can we make?

In this case, note that the team $\{A,B,C\}$ is the same as the team $\{A,C,B\}$ or $\{B,A,C\}$. In other words, the order in which the team members are selected does not matter. Such arrangements in which order does not matter are called Combinations. We can use the fundamental counting principle to come up with a formula for finding the total number of combinations.

For instance, in the example discussed above, if we assume that order does matter, then as discussed in the previous section, by the counting principle, we will have $4 \times 3 \times 2 \times 1$ possible arrangements. Now for any given arrangement, let’s say $\{A, B, C\}$,  there are many possibilities such as $\{A, C, B\}$ or $\{B, A, C\}$ that result in the same combination. So, we need to figure out the total number of possibilities for any given arrangement that leads to the same team.

Since we have three slots and three members (i.e., $A$, $B$, $C$), so we can fill the first slot in three different ways, the second slot in 2 different ways, and the third slot in one different way. By the fundamental counting principle, we will have $3 \times 2 \times 1$ possibilities that lead to the same combination.

So the total number of unique combinations would be

$\large{\frac{4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}}$

Generally, if we have $n$ objects and we choose $r$ objects to make a combination, the total number of combinations is denoted by $C(n,r)$ and is given as

$C(n,r) = \frac{n \times n-1 \times n-2 \times \cdots n-r}{r \times r-1 \times r-2 \times \cdots 1}$

Multiplying both numerator and denominator by $(n-r)!$ and using the factorial rule , we can simplify the formula as

$C(n,r) = \frac{n!}{r!(n-r)!}$

A locker is locked with a four-digit password. The password only contains numbers from $0-6$. How many different password options will you have if the order of numbers does that matter?

We have seven numbers to choose from and we have to make a $4$ digit password, hence $n=7$ and $r=4$, in this case. The total number of combinations is given as

$C(7,4) = \frac{7!}{4!(7-4)!}$

$C(7,4) = \frac{7 \times 6 \times 5 \times 4!}{4!3!}$

$C(7,4) = \frac{7 \times 6 \times 5}{3!} = 35$

1. We have a group of four people; let’s call those Jhon, Jill, Liz, and Tom. We wish to make the team consisting of three people using the available group. However, Liz must be included in every team. How many distinct teams can we make?

2. Kevin wants to buy a new Honda car. The car is available in 4 different models, and every model has 5 different colors. Calculate the total amount of choices.

3. A coin is flipped 3 times. Draw a tree diagram and calculate the total amount of possible outcomes using the counting principle

4. Freya went to an ice cream shop. The menu has 2 cones available Large and Small, and both the cones are available in 3 different shapes. Flavors available for large cones are Vanilla, Mango, Chocolate, and Strawberry, while small cones also include all the flavors except Mango. How many choices does Freya have?  

5.A restaurant has 6 different Appetizers, 5 different desserts, and 7 different meal options. Calculate the total number of options for given deals

a) Deal 1: It includes Appetizers and a meal.

b) Deal 2: Desserts and a meal.

c) Deal 3: Appetizers, a meal, and desserts.

2. The car is available in 4 different models and 5 different colors. So, by the rule of counting principle total number of choices are $ 4\times5 = 20$.

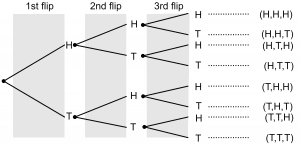
The first flip results in $2$ possible outcomes, so do the second and the third flip. Hence by the counting principle, the total possible outcomes will be $2 \times 2 \times 2 = 8$, which is also confirmed by the tree diagram.

Freya has two different cones available large and small, which are mutually exclusives and cannot happen together. So, we will calculate possible outcomes for each and then add them up.

Total number of options for large cone ice-cream:   $ 3\times4= 12$

Total number of options for small cone ice-cream: $ 3\times3 = 9$

Total number of possible options: $ 12+9 = 21$

a) Total number of options for deal 1 : $ 6\times7 = 42$.

b) Total number of options for deal 2: $ 5\times7= 35$.

c) Total number of options for deal 3: $ 6\times7\times5 = 210$.

Previous Lesson  |  Main Page | Next Lesson

Fundamental Counting Principle

These lessons, with videos, examples and step-by-step solutions, help Algebra II students learn about fundamental counting principle.

Related Pages Permutations & Combinations More Algebra II Lessons

The following figure shows the Fundamental Counting Principle. Scroll down the page for more examples and step by step solutions.

What is the Fundamental Counting Principle? Given a set of possible events, we often want to find the number of outcomes that can result. We can do this using the fundamental counting principal. For example, the fundamental counting principal can be used to calculate the number of possible lottery ticket combinations. The fundamental counting principal can be used in day to day life and is encountered often in probability. The fundamental counting principle states that if there are ’m' ways for one event to occur and ‘n’ ways for another, there are m × n ways for both to occur.

How to use the fundamental counting principle?

Example: A sandwich comes with a choice of soda or tea and a side of fries, chips, slaw or salad. Find the number of different combo.

Examples of using the fundamental counting principle

Example 1: An apartment complex offers apartments with four different options, designated by A through D. A: One Bedroom, Two Bedrooms, Three Bedrooms B. One Bathroom, Two Bathrooms C. First Floor, Second Floor D. Lake View, Golf Course View, No Special View How many apartment options are available? Describe two such options.

Example 2: A car model comes in nine colors, with or without air conditioning, with or without sunroof, with or without automatic transmission, and with or without antilock brakes. In how many ways can the ca be ordered with regard to these options.

Example 3: How many different four-letter radio station call letters can letters van be formed if the first letter must be W or K?

Example 4: A social security number contains nine digits, such as 074-66-7795. How many different social security numbers can be formed?

How to distinguish between the Sum Counting Principle and the Product Counting Principle? This video demonstrates how to find the total possible number of options for given situations. For example if you have 3 shirts, two pants and 4 hats, how many different outfits can you pick?

Examples for the sum counting principle:

I have 3 red hats and 2 green hats. If I choose one hat, how many ways can I choose a hat?

On a number cube there are 3 even numbers and 1 multiple of five. If you roll the cube, how many ways can you get an even number or a multiple of 5?

Examples for the product counting principle: Jim has 3 pairs of pants, 2 shirts and 2 hats, how many different ways can he dress? Which principle should be used?

Jim has a box of coins, it has 200 pennies, 2 nickels, 3 dimes, and 5 quarters. By choosing one coin, how many ways can he get more than 6 cents.

MaryBeth has 3 types of bagels in the fridge, 2 types of cream cheeze and 3 veggies. If she wants one of each, how many different lunch options does she have?

Multiplication Principle - Counting Techniques A fundamental idea to count the number of ways that some event can happen.

How many different combinations can be made for a briefcase that has a 3-dial lock with each dial having numbers 0-9 available?

How many license plates can be made if the first 3 entries must be letters, followed by 3 numbers?

Suppose you take a multiple choice exam that has 10 questions, each question has 5 answers. How many different ways could the exam be answered?

How the fundamental counting principle can help you determine the number of possible outcomes or combinations very quickly?

You flip a coin and spin the spinner. How many outcomes are possible?

You pick a marble and roll a die. How many outcomes are possible?

Hunter wants to buy a new pair of skates. He can buy speed skates, figure skates, or hockey skates. A pair of skates can come in blue or silver, and can be decorated with blue streaks or green clovers. How many different combinations can Hunter choose from?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Reset password New user? Sign up

Existing user? Log in

Fundamental Counting Principle

Already have an account? Log in here.

The fundamental counting principle is a rule used to count the total number of possible outcomes in a situation. It states that if there are \( n\) ways of doing something, and \( m\) ways of doing another thing after that, then there are \( n\times m\) ways to perform both of these actions. In other words, when choosing an option for \(n\) and an option for \(m\), there are \( n\times m\) different ways to do both actions.

Basic Examples

Intermediate examples, problem solving.

Lily is trying to decide what to wear. She has shirts in the following colors: red, purple, and blue, and she has pants in the following colors: black and white. How many different outfits can Lily choose from (assuming she selects one shirt and one pair of pants)? We know from the definition of the rule of product that if there are \(n\) options for doing one thing (like choosing a shirt), and \(m\) options for doing another thing (like choosing a pair of pants), then there are \(n \times m\) total combinations we can choose from. In this case, there are \(3\) options for choosing a shirt, and there are \(2\) options for choosing pants. Thus, there are \(3 \times 2 = 6\) total options. Here is a table where each row represents a possible outfit. Shirt Pants Red Black Blue Black Purple Black Red White Blue White Purple White As expected, there are \(6\) possible combinations. \(_\square\)

In the example above, there were two things to choose: a shirt and a pair of pants. However, the rule of product can extend to however many things to choose from. For example, if there are \(n\) choices for a shirt, \(m\) choices for a pair of pants, \(x\) choices for a pair of shoes, and \(y\) choices for a hat, the rule of product states that there are \(n \times m \times x \times y\) total possible combinations.

You go to check out three books at the library, and you want one history book, one science book, and one fantasy book.

The library has 50 history books, 95 fantasy novels, and 30 books about science. How many combinations of books do you have to choose from?

There are \(8\) daily newspapers and \(5\) weekly magazines published in Chicago. If Colin wants to subscribe to exactly one daily newspaper and one weekly magazine, how many different choices does he have? Colin has \(8\times5=40\) choices. \(_\square\)

Calvin wants to go to Milwaukee. He can choose from \(3\) bus services or \(2\) train services to head from home to downtown Chicago. From there, he can choose from 2 bus services or 3 train services to head to Milwaukee. How many ways are there for him to get to Milwaukee? Since Calvin can either take a bus or a train downtown , he has \( 3+2 =5\) ways to head downtown (Rule of sum). After which, he can either take a bus or a train to Milwaukee, and hence he has another \( 2+3=5\) ways to head to Milwaukee (Rule of sum). Thus in total, he has \( 5 \times 5 = 25\) ways to head from home to Milwaukee (Rule of product). \(_\square\)

Six friends Andy, Bandy, Candy, Dandy, Endy, and Fandy want to sit in a row at the cinema. If there are only six seats available, how many ways can we seat these friends? For the first seat, we have a choice of any of the 6 friends. After seating the first person, for the second seat, we have a choice of any of the remaining 5 friends. After seating the second person, for the third seat, we have a choice of any of the remaining 4 friends. After seating the third person, for the fourth seat, we have a choice of any of the remaining 3 friends. After seating the fourth person, for the fifth seat, we have a choice of any of the remaining 2 friends. After seating the fifth person, for the sixth seat, we have a choice of only 1 of the remaining friends. Hence, by the rule of product, there are \( 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720\) ways to seat these 6 people. More generally, this problem is known as a permutation . There are \( n! = n \times (n-1) \times (n-2) \times \cdots \times 1\) ways to seat \( n\) people in a row. \(_\square\)

My toy piano keyboard has 7 distinct white notes: letters A-G in English alphabet. I'm going to create a melody by playing three random notes. I am not allowed to repeat any notes and the melody cannot be ended with E, F or G. How many different melodies can I play?

• C G A is permitted.
• A F A isn't permitted because of repetition.
• A B E is not permitted because of last note rule.

How many positive divisors does \( 2000 = 2^4 5^3\) have? Any positive divisor of 2000 must have the form \( 2^a 5^b\), where \( a\) and \( b\) are integers satisfying \( 0 \leq a \leq 4, 0 \leq b \leq 3\). There are 5 possibilities for \( a\) and 4 possibilities for \( b\), hence there are \( 5 \times 4 = 20\) (rule of product) positive divisors of 2000 in all. \(_\square\)

• Problem solving
• Rule of Sum
• Permutations

Problem Loading...

Note Loading...

Set Loading...

THE FUNDAMENTAL COUNTING PRINCIPLE

This plan will introduce Mathletes to The Fundamental Counting Principle – a faster method to determining the total number of possible outcomes of an event without listing them all out!

Download the Mathlete handout.

Download the coaches version with solutions.

Fundamental Counting Principle

In this mini-lesson, we will explore the fundamental counting principle by learning about the fundamental counting principle meaning, using the  fundamental counting principle examples while discovering the interesting facts around them.

Here's a fundamental counting principle calculator. Enter the values and check how this principle works.

Lesson Plan

What is the fundamental counting principle.

The fundamental counting principle is a rule to count all the possible ways for an event to happen or the total number of possible outcomes in a situation.

It states that when there are \( n \)  ways to do one thing, and \( m \) ways to do another thing, then the number of ways to do both the things can be obtained by taking their product. This is expressed as \( n \times m \).

How to Use the Fundamental Counting Principle to Determine Sample Space?

Let's get acquainted with sample space  first.

Sample space is referred to as the collection of all possible outcomes in any random experiment.

Now, that we know what is sample space, let's see the use of the fundamental counting principle to determine sample space.

Let's see a few fundamental counting principle examples to understand this concept better.

Claire has \(2\) shirts and \(2\) skirts of different colors in her closet. The colors of the shirts are pink and black, while the colors of the skirt are black and white. She wore one of the combinations, which were a pink shirt and a white skirt. What do you think are the other possible combinations she could try?

She could wear any of the following \(3\) combinations apart from the one which is worn by her.

This means using the 2 shirts and 2 skirts, she could dress up in 4 different ways.

If we the apply the fundamental counting principle, we get to know that she can wear either the pink shirt or the black  shirt. Similarly, she can either wear the white skirt or the black skirt.

Hence, she can wear her shirts in 2 ways and skirts in 2 ways. To get the total number of combinations possible, we take the product of 'the number of ways in which she can wear her shirt' with 'the number of ways she can wear her skirt'. Hence, the number of combinations are represented as \( 2 \times 2 = 4 \). This shows that the sample space is 4

Brad has 2 bananas, 3 apples and 3 oranges in a basket. In how many different ways can he consume the fruits in the basket?

Applying the above rules, we know that the total number of ways in which he can consume the fruits in the basket  is:  \( 2 \times 3 \times 3 = 18 \).

Hence, he has 18 different ways to consume the fruits. This tells us that 18 is the sample space in this case.

Any choice made by him will be within these 18 ways.

• It is possible to find the sample space without writing it down, using the fundamental counting principle.
• The fundamental counting principle is also used when the sample space is very large. This eases the trouble of writing it down. It can be used in probability as well.

Solved Examples

Wendy went to buy an ice cream from a seller who sells 3 different flavors of ice creams, vanilla, chocolate and strawberry and he gives 6 different choices for cones. How many choices does she have?

The ice cream seller sells 3 flavors of ice creams, vanilla, chocolate and strawberry giving his customers 6 different choices of cones.

Wendy has 3 choices for the ice cream flavors and 6 choices for the ice cream cones.

Hence, by the fundamental counting principle, the number of choices that Wendy can be given are \( 3 \times 6 = 18 \).

Wendy can choose from any of the 18 possible combinations.

Ashton knows there are 7 daily newspapers and 4 weekly magazines published in his town. If he wants to subscribe to one daily newspaper and one weekly magazine, how many choices does he have?

Ashton knows there are 7 daily newspapers and 4 weekly magazines published in his town.

He will apply the fundamental counting principle to calculate the choices that he has.

Hence, Ashton will take the product of "the number of ways in which he can select a daily newspaper" and "the number of ways in which he can select a weekly magazine".

The number of choices will be calculated as \( 7 \times 4 = 28 \).

There are 6 children in a classroom and 6 benches for them to sit. The class teacher makes them sit at a different place every month. In how many ways can she make them sit in the classroom?

There are 6 children and 6 benches for them to sit.

Hence, their teacher will apply the fundamental counting principle to find the number of ways in which she can make them sit.

The number of ways in which she can make the children sit in the classroom is \( 6 \times 6 = 36 \).

Interactive Questions

Here are a few activities for you to practice.

Select/Type your answer and click the "Check Answer" button to see the result.

• Lily has 4 shirts, 3 pants, 2 pairs of shoes and 3 handbags. In how many ways can she choose her outfits such that she selects 1 shirt, 1 pant, 1 pair of shoes and 1 handbag ?
• Christopher went to a library to get a novel and a history book. There are 60 novels and 148 history books in the library. How many combinations of books can he choose? 

Let's Summarize

The mini-lesson targeted the fascinating concept of fundamental counting principle. The math journey around fundamental counting principle starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.

About Cuemath

At Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

Frequently Asked Questions (FAQs)

1. what is the difference between fundamental counting principle and permutation.

In a problem, where the objects can be repeated, permutation cannot be used. In such cases the fundamental counting principle is used.

2. What is r in the combination formula?

In the combination formula,"r" represents the number of items that can be chosen at once.

3. Why is the fundamental counting principle important?

The fundamental counting principle can be used for problems having large sample spaces, problems having more than two choices and can also be applied in probability.

• Live one on one classroom and doubt clearing
• Practice worksheets in and after class for conceptual clarity
• Personalized curriculum to keep up with school

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: The Fundamental Principle of Counting

• Last updated
• Save as PDF
• Page ID 40933

• Richard W. Beveridge
• Clatsop Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Combinatorics is a major area of what is generally known as "Discrete Mathematics." The word discrete refers to quantities that are individual, separate or distinct. This creates a major division in mathematics between "continuous mathematics" and "discrete mathematics." The difference between these two areas is that continuous mathematics considers and uses all parts of the number line whole numbers, rational numbers (fractions), irrational numbers and so forth. Discrete mathematics typically uses only the whole numbers.

Rather than limiting the possibilities in mathematics, this restriction actually opens amazing new areas of consideration. The binary codes that computers use are generally controlled and kept (mostly) error free through the use of discrete mathematics. Computer security for the simplest (checking your on-line bank balance) and the most complex (high level classified data) digital information is handled through encryption that relies on the concepts of discrete mathematics.

Any type of application in the sciences that involves choices and possibilities often uses the concepts of combinatorics. Combinatorial chemistry explores the results when a series of different chemical groups are added to the same basic chemical structure to investigate the qualities of the resulting compound. In addition, combinatorics is very important to the study of probability. In order to calculate the probability of an event, it is often necessary to calculate how many

different ways something can happen. The first major idea of combinatorics is the fundamental principle of counting. This is the idea that if two events occur in succession and there are \(m\) ways to do the first one and \(n\) ways to do the second (after the first has occurred), then there are \(m * n\) ways to complete the two tasks in succession.

All of the possibilities are listed out and can be constructed from the tree diagram. Here are some sample problems for using the fundamental principle of counting (also known as the multiplication principle). Example : An ice cream shop offers Vanilla, Chocolate, Strawberry, Boysenberry and Rocky Road ice cream. The ice cream comes with either a waffle cone, a sugar cone or a wafer cone and can be plain or with sprinkles. How many different ways are there to order a single scoop of ice cream?

With 5 different types of ice cream, 3 different cones and 2 choices for sprinkles, there would be \(5 * 3 * 2=30\) different possibilities. Example : In many states the license plates for automobiles consist of three letters followed three numbers. How many different possibilities are there: if repetition of letters and numbers is allowed? if repetition of letters and numbers is not allowed? There are six positions for letters and numbers that make up the license plate. The first three are to be letters and the second three numbers. There are 26 choices for the first three and 10 choices for the second three, so there are \(26 * 26 * 26 * 10 * 10 * 10=17,576,000\) possible license plates if repetition is allowed.

If repetition is not allowed then we have to discount whichever letter or number is chosen for a particular position. So, for the first letter there are 26 possibilities, but then only 25 for the second letter and 24 for the third. Likewise, with the numbers there are 10 choices initially, then 9 choices and then 8 So, the solution without repetition would be \(26 * 25 * 24 * 10 * 9 * 8=11,232,000\)

4) \(\quad\) A coin is flipped five times and the result each time is recorded. How many different possible outcomes are there? 5) \(\quad\) A coin is flipped and a six-sided die is rolled and the results are recorded. If this is done three times, how many possible outcomes are there? 6) \(\quad\) Two cards are chosen from a deck of 52 cards. If the first card is not replaced before the second card is chosen, how many ways are there to choose: a) \(\quad\) A spade first and a heart second? b) \(\quad\) Two spades? 7) \(\quad\) A company has 3000 employees. They plan to implement an employee ID numbering system that would consist of a letter followed by two digits. Is it possible to give each employee a different ID code under this plan? 8) \(\quad\) A baseball team has 7 pitchers and 3 catchers. How many different batteries (pitcher - catcher combinations) are possible? 9) \(\quad\) A string of five letters is created using the letters \(\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}\) and E. How many of these letter strings are possible if: \(\quad\) a) \(\quad\) No conditions are imposed \(\quad\) b) Repetition of the letter \(A\) is not allowed \(\quad\) c) Each letter string must begin with \(C\) \(\quad\) d) \(\quad\) B must be the middle letter \(\quad\) e) \(\quad\) \(A, B\) and \(C\) must be the middle letters in any order with no repetition For Part (e) please list all possibilities. 10) (\quad\) A combination lock is numbered from 0 to 30. Each combination consists of three numbers in succession. Successive numbers must be different, but the first and third can be the same. How many different combinations are possible?

You are using an outdated browser and it's not supported. Please upgrade your browser to improve your experience.

• LOGIN FOR PROGRAM PARTICIPANTS
• PROGRAM SUPPORT

Counting Rules—The Fundamental Counting Principle and Permutations

Description.

There may be cases when our downloadable resources contain hyperlinks to other websites. These hyperlinks lead to websites published or operated by third parties. UnboundEd and EngageNY are not responsible for the content, availability, or privacy policies of these websites.

• Precalculus Module 5, Topic A, Lesson 2: Student Version
• Precalculus Module 5, Topic A, Lesson 2: Teacher Version

Related Guides and Multimedia

Our professional learning resources include teaching guides, videos, and podcasts that build educators' knowledge of content related to the standards and their application in the classroom.

There are no related guides or videos. To see all our guides, please visit the Enhance Instruction section here .

FUNDAMENTAL PRINCIPLE OF COUNTING PROBLEMS WITH SOLUTION

Problem 1 :

A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?

Number of ways of selecting Chinese food items  =  7

Number of ways of selecting Indian food items  =  10

Here a person may choose any one food items, either an Indian or a Chinese food. So, we have to use "Addition" to find the total number of ways for selecting the food item.

Total number of selecting Indian or a Chinese food 

=  10 + 7  =  17 ways

Problem 2 :

There are 3 types of toy car and 2 types of toy train available in a shop. Find the number of ways a baby can buy a toy car and a toy train?

According to the given question, a baby wants to buy both toy car and toy train. So we have to use the binary operation "Multiplication" to find the total number of ways.

Types of car available in the shop  =  3

Types of car available in the shop  =  2

Total number of ways of buying a car  =  3 (2)  =  6

Problem 3 :

How many two-digit numbers can be formed using 1,2,3,4,5 without repetition of digits?

In order to form a two digit number, we have to select two numbers out of the given 5 numbers. 

___  ___

To fill up the first dash, we have 5 options.

To fill up the second dash, we have 4 options.

Number of two digit numbers formed using the above numbers  =  5 (4)  =  20.

Problem 4 :

Three persons enter in to a conference hall in which there are 10 seats. In how many ways they can take their seats?

1 st person may choose 1 seat out of 10 seats

2 nd person may choose 1 seat out of 9 seats

3 rd person may choose 1 seat out of 8 seats

Total number of ways of selecting seat  =  10 (9) (8)

  =  720 ways

Problem 5 :

In how many ways 5 persons can be seated in a row?

5 persons may sit in 5 seats.

1st person may sit any one of the 5 seats 

2nd person may sit any one of the 4 seats and so on.

Hence the total number of ways  =  5  ⋅ 4  ⋅ 3  ⋅ 2  ⋅ 1

 =  120 ways

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

How to Find the Vertex of a Parabola

May 12, 24 10:03 PM