1 tailed hypothesis

Statistics with Python
Data Analysis Tutorial
Python â€“ Data visualization tutorial
Machine Learning Projects
Machine Learning Interview Questions
Machine Learning Mathematics
Deep Learning Tutorial
Deep Learning Project
Deep Learning Interview Questions
Computer Vision Tutorial
Computer Vision Projects
NLP Project
NLP Interview Questions
100 Days of Machine Learning

Difference Between One-Tailed and Two-Tailed Tests

One and Two-Tailed Tests are ways to identify the relationship between the statistical variables. For checking the relationship between variables in a single direction (Left or Right direction), we use a one-tailed test. A two-tailed test is used to check whether the relations between variables are in any direction or not.

One-Tailed Test

A one-tailed test is based on a uni-directional hypothesis where the area of rejection is on only one side of the sampling distribution. It determines whether a particular population parameter is larger or smaller than the predefined parameter. It uses one single critical value to test the data.

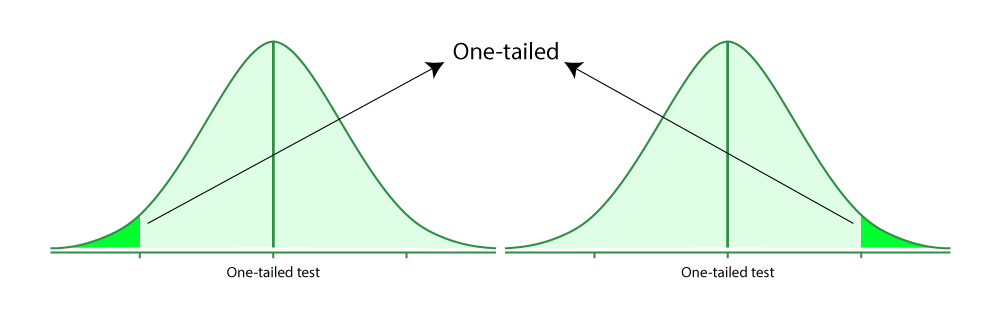
Alternative Hypothesis ( H 1):

$H_1: \theta > \theta_0$

Test Statistic: Depending on the type of test and the distribution, the test statistic is computed ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in the critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of participants of students in coding competition on their fear level.

H0: There is no important effect of students in coding competition on their fear level.

The main intention is to check the decreased fear level when students participate in a coding competition.

Two-Tailed Test

A two-tailed test is also called a nondirectional hypothesis. For checking whether the sample is greater or less than a range of values, we use the two-tailed. It is used for null hypothesis testing.

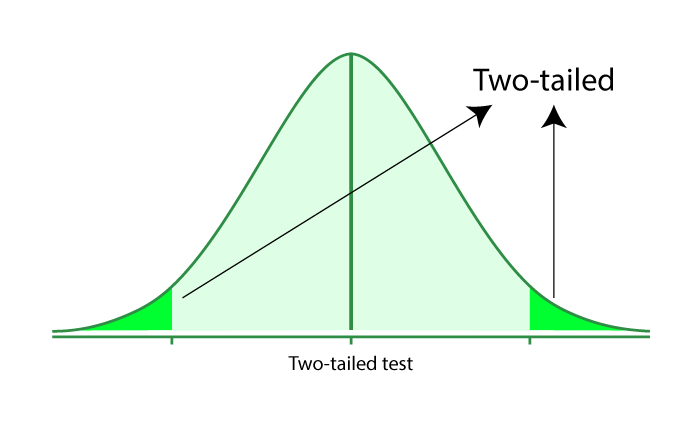
Test Statistic: Compute the test statistic as appropriate for the distribution ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in either tail of the distribution’s critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of new bill pass on the loan of farmers.

H0: There is no significant effect of the new bill passed on loans of farmers.

New bill passes can affect in both ways either increase or decrease the loan of farmers.

Difference Between One and Two-Tailed Test:

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Skip to primary navigation
Skip to main content
Skip to primary sidebar

Statistical Methods and Data Analytics

FAQ: What are the differences between one-tailed and two-tailed tests?

When you conduct a test of statistical significance, whether it is from a correlation, an ANOVA, a regression or some other kind of test, you are given a p-value somewhere in the output. If your test statistic is symmetrically distributed, you can select one of three alternative hypotheses. Two of these correspond to one-tailed tests and one corresponds to a two-tailed test. However, the p-value presented is (almost always) for a two-tailed test. But how do you choose which test? Is the p-value appropriate for your test? And, if it is not, how can you calculate the correct p-value for your test given the p-value in your output?

What is a two-tailed test?

First let’s start with the meaning of a two-tailed test. If you are using a significance level of 0.05, a two-tailed test allots half of your alpha to testing the statistical significance in one direction and half of your alpha to testing statistical significance in the other direction. This means that .025 is in each tail of the distribution of your test statistic. When using a two-tailed test, regardless of the direction of the relationship you hypothesize, you are testing for the possibility of the relationship in both directions. For example, we may wish to compare the mean of a sample to a given value x using a t-test. Our null hypothesis is that the mean is equal to x . A two-tailed test will test both if the mean is significantly greater than x and if the mean significantly less than x . The mean is considered significantly different from x if the test statistic is in the top 2.5% or bottom 2.5% of its probability distribution, resulting in a p-value less than 0.05.

What is a one-tailed test?

Next, let’s discuss the meaning of a one-tailed test. If you are using a significance level of .05, a one-tailed test allots all of your alpha to testing the statistical significance in the one direction of interest. This means that .05 is in one tail of the distribution of your test statistic. When using a one-tailed test, you are testing for the possibility of the relationship in one direction and completely disregarding the possibility of a relationship in the other direction. Let’s return to our example comparing the mean of a sample to a given value x using a t-test. Our null hypothesis is that the mean is equal to x . A one-tailed test will test either if the mean is significantly greater than x or if the mean is significantly less than x , but not both. Then, depending on the chosen tail, the mean is significantly greater than or less than x if the test statistic is in the top 5% of its probability distribution or bottom 5% of its probability distribution, resulting in a p-value less than 0.05. The one-tailed test provides more power to detect an effect in one direction by not testing the effect in the other direction. A discussion of when this is an appropriate option follows.

When is a one-tailed test appropriate?

Because the one-tailed test provides more power to detect an effect, you may be tempted to use a one-tailed test whenever you have a hypothesis about the direction of an effect. Before doing so, consider the consequences of missing an effect in the other direction. Imagine you have developed a new drug that you believe is an improvement over an existing drug. You wish to maximize your ability to detect the improvement, so you opt for a one-tailed test. In doing so, you fail to test for the possibility that the new drug is less effective than the existing drug. The consequences in this example are extreme, but they illustrate a danger of inappropriate use of a one-tailed test.

So when is a one-tailed test appropriate? If you consider the consequences of missing an effect in the untested direction and conclude that they are negligible and in no way irresponsible or unethical, then you can proceed with a one-tailed test. For example, imagine again that you have developed a new drug. It is cheaper than the existing drug and, you believe, no less effective. In testing this drug, you are only interested in testing if it less effective than the existing drug. You do not care if it is significantly more effective. You only wish to show that it is not less effective. In this scenario, a one-tailed test would be appropriate.

When is a one-tailed test NOT appropriate?

Choosing a one-tailed test for the sole purpose of attaining significance is not appropriate. Choosing a one-tailed test after running a two-tailed test that failed to reject the null hypothesis is not appropriate, no matter how "close" to significant the two-tailed test was. Using statistical tests inappropriately can lead to invalid results that are not replicable and highly questionable–a steep price to pay for a significance star in your results table!

Deriving a one-tailed test from two-tailed output

The default among statistical packages performing tests is to report two-tailed p-values. Because the most commonly used test statistic distributions (standard normal, Student’s t) are symmetric about zero, most one-tailed p-values can be derived from the two-tailed p-values.

Below, we have the output from a two-sample t-test in Stata. The test is comparing the mean male score to the mean female score. The null hypothesis is that the difference in means is zero. The two-sided alternative is that the difference in means is not zero. There are two one-sided alternatives that one could opt to test instead: that the male score is higher than the female score (diff > 0) or that the female score is higher than the male score (diff < 0). In this instance, Stata presents results for all three alternatives. Under the headings Ha: diff < 0 and Ha: diff > 0 are the results for the one-tailed tests. In the middle, under the heading Ha: diff != 0 (which means that the difference is not equal to 0), are the results for the two-tailed test.

Two-sample t test with equal variances ------------------------------------------------------------------------------ Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- male | 91 50.12088 1.080274 10.30516 47.97473 52.26703 female | 109 54.99083 .7790686 8.133715 53.44658 56.53507 ---------+-------------------------------------------------------------------- combined | 200 52.775 .6702372 9.478586 51.45332 54.09668 ---------+-------------------------------------------------------------------- diff | -4.869947 1.304191 -7.441835 -2.298059 ------------------------------------------------------------------------------ Degrees of freedom: 198 Ho: mean(male) - mean(female) = diff = 0 Ha: diff < 0 Ha: diff != 0 Ha: diff > 0 t = -3.7341 t = -3.7341 t = -3.7341 P < t = 0.0001 P > |t| = 0.0002 P > t = 0.9999

Note that the test statistic, -3.7341, is the same for all of these tests. The two-tailed p-value is P > |t|. This can be rewritten as P(>3.7341) + P(< -3.7341). Because the t-distribution is symmetric about zero, these two probabilities are equal: P > |t| = 2 * P(< -3.7341). Thus, we can see that the two-tailed p-value is twice the one-tailed p-value for the alternative hypothesis that (diff < 0). The other one-tailed alternative hypothesis has a p-value of P(>-3.7341) = 1-(P<-3.7341) = 1-0.0001 = 0.9999. So, depending on the direction of the one-tailed hypothesis, its p-value is either 0.5*(two-tailed p-value) or 1-0.5*(two-tailed p-value) if the test statistic symmetrically distributed about zero.

In this example, the two-tailed p-value suggests rejecting the null hypothesis of no difference. Had we opted for the one-tailed test of (diff > 0), we would fail to reject the null because of our choice of tails.

The output below is from a regression analysis in Stata. Unlike the example above, only the two-sided p-values are presented in this output.

Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 2, 197) = 46.58 Model | 7363.62077 2 3681.81039 Prob > F = 0.0000 Residual | 15572.5742 197 79.0486001 R-squared = 0.3210 -------------+------------------------------ Adj R-squared = 0.3142 Total | 22936.195 199 115.257261 Root MSE = 8.8909 ------------------------------------------------------------------------------ socst | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- science | .2191144 .0820323 2.67 0.008 .0573403 .3808885 math | .4778911 .0866945 5.51 0.000 .3069228 .6488594 _cons | 15.88534 3.850786 4.13 0.000 8.291287 23.47939 ------------------------------------------------------------------------------

For each regression coefficient, the tested null hypothesis is that the coefficient is equal to zero. Thus, the one-tailed alternatives are that the coefficient is greater than zero and that the coefficient is less than zero. To get the p-value for the one-tailed test of the variable science having a coefficient greater than zero, you would divide the .008 by 2, yielding .004 because the effect is going in the predicted direction. This is P(>2.67). If you had made your prediction in the other direction (the opposite direction of the model effect), the p-value would have been 1 – .004 = .996. This is P(<2.67). For all three p-values, the test statistic is 2.67.

Your Name (required)

Your Email (must be a valid email for us to receive the report!)

Comment/Error Report (required)

How to cite this page

Key Differences

Know the Differences & Comparisons

Difference Between One-tailed and Two-tailed Test

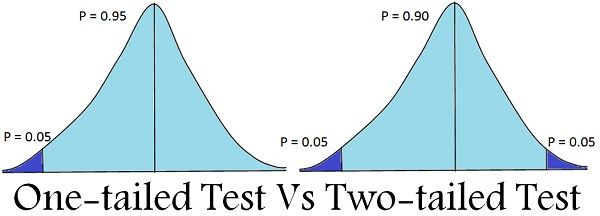
To test the hypothesis, test statistics is required, which follows a known distribution. In a test, there are two divisions of probability density curve, i.e. region of acceptance and region of rejection. the region of rejection is called as a critical region .

In the field of research and experiments, it pays to know the difference between one-tailed and two-tailed test, as they are quite commonly used in the process.

Content: One-tailed Test Vs Two-tailed Test

Comparison chart, definition of one-tailed test.

One-tailed test alludes to the significance test in which the region of rejection appears on one end of the sampling distribution. It represents that the estimated test parameter is greater or less than the critical value. When the sample tested falls in the region of rejection, i.e. either left or right side, as the case may be, it leads to the acceptance of alternative hypothesis rather than the null hypothesis. It is primarily applied in chi-square distribution; that ascertains the goodness of fit.

In this statistical hypothesis test, all the critical region, related to α , is placed in any one of the two tails. One-tailed test can be:

Left-tailed test : When the population parameter is believed to be lower than the assumed one, the hypothesis test carried out is the left-tailed test.
Right-tailed test : When the population parameter is supposed to be greater than the assumed one, the statistical test conducted is a right-tailed test.

Definition of Two-tailed Test

The two-tailed test is described as a hypothesis test, in which the region of rejection or say the critical area is on both the ends of the normal distribution. It determines whether the sample tested falls within or outside a certain range of values. Therefore, an alternative hypothesis is accepted in place of the null hypothesis, if the calculated value falls in either of the two tails of the probability distribution.

In this test, α is bifurcated into two equal parts, placing half on each side, i.e. it considers the possibility of both positive and negative effects. It is performed to see, whether the estimated parameter is either above or below the assumed parameter, so the extreme values, work as evidence against the null hypothesis.

Key Differences Between One-tailed and Two-tailed Test

The fundamental differences between one-tailed and two-tailed test, is explained below in points:

One-tailed test, as the name suggest is the statistical hypothesis test, in which the alternative hypothesis has a single end. On the other hand, two-tailed test implies the hypothesis test; wherein the alternative hypothesis has dual ends.
In the one-tailed test, the alternative hypothesis is represented directionally. Conversely, the two-tailed test is a non-directional hypothesis test.
In a one-tailed test, the region of rejection is either on the left or right of the sampling distribution. On the contrary, the region of rejection is on both the sides of the sampling distribution.
A one-tailed test is used to ascertain if there is any relationship between variables in a single direction, i.e. left or right. As against this, the two-tailed test is used to identify whether or not there is any relationship between variables in either direction.
In a one-tailed test, the test parameter calculated is more or less than the critical value. Unlike, two-tailed test, the result obtained is within or outside critical value.
When an alternative hypothesis has ‘≠’ sign, then a two-tailed test is performed. In contrast, when an alternative hypothesis has ‘> or <‘ sign, then one-tailed test is carried out.

To sum up, we can say that the basic difference between one-tailed and two-tailed test lies in the direction, i.e. in case the research hypothesis entails the direction of interrelation or difference, then one-tailed test is applied, but if the research hypothesis does not signify the direction of interaction or difference, we use two-tailed test.

You Might Also Like:

Swati Aggarwal says

April 24, 2018 at 11:47 am

Very Informative and specifically summarised. thank you.

Aurobindo says

January 20, 2019 at 8:22 am

Amazing Surbhi. I recently started following this site and I really find it very very useful. The simplicity of language, the key distinctions, range of depth covered in giving the differences. Hats off to you for your effort. Very amazing. I have definitely bookmarked this website as ‘my favorite’ and I shall keep visiting it again and again. Keep it up. Thanks.

Marian Truehill says

July 23, 2020 at 11:48 pm

This website is very useful and easy to understand for Statistics methods and concepts.

Kuje Samson says

January 11, 2023 at 5:13 am

The website is very linear to a layman statistics. I really enjoyed visiting the site