One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
This topic is relevant for:


Inverse Proportion
Here we will learn about inverse proportion, including what inverse proportion is and how to solve inverse proportion problems including real-life problem solving. We will also have a look at the inverse proportionality formula.
There are also inverse proportion worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is inverse proportion?
Inverse proportion is a type of proportionality relationship. If two quantities are inversely proportional then as one quantity increases, the other decreases.
An example of inverse proportion would be the hours of work required to build a wall. If there are more people building the same wall, the time taken to build the wall reduces.
Conversely, an example of direct proportion would be that the area of a circle is directly proportional to its radius.
Inverse proportion is also known as indirect proportion or inverse variation .
Inverse proportion is applied to real life problems such as the speed of a moving object, determining whether an item will float or sink in water, or the time taken to complete a finite task whereas direct proportion is useful in numerous real life situations such as exchange rates, conversion between units, and fuel prices.
To determine the value of a variable that is inversely proportional to another, we need to determine the relationship between the two variables and then use this to find our unknown value.
Similar to a directly proportional relationship, we need to determine the constant of proportionality, k.
Step-by-step guide: Direct proportion

Inverse proportion formula
The symbol \propto is the proportionality symbol and it represents a proportional relationship between two variables. If it is inversely proportional to x, we write this relationship as y\propto\frac{1}{x}.
This relationship can be described using an equivalence relationship. When y is inversely proportional to x , the value of x \times y is a constant value. This value is the constant of proportionality and we use the letter k to denote this value. Using a formula, we have k=xy.
Rearranging this formula to make y the subject, we obtain the inverse proportion formula,
y=\frac{k}{x} .
Step-by-step guide: Inverse proportion formula
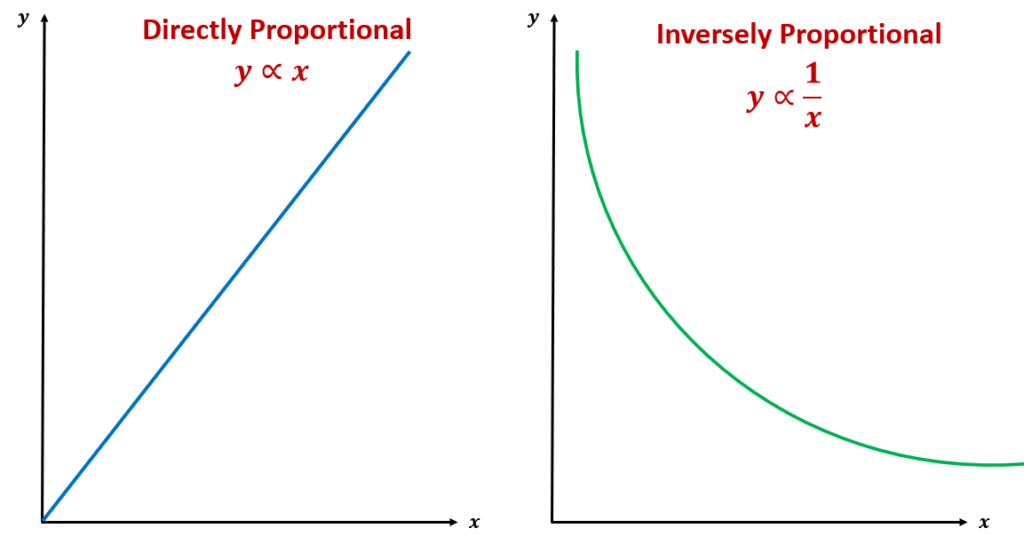
Graphs representing an inverse proportion between two variables
Proportional relationships can also be represented by graphs. If we sketched a graph of the line y=\frac{k}{x}, as x increases in size, k is being divided by a larger number and so the result is a value y that gets increasingly smaller. This gives us the curved line graph of the reciprocal function.
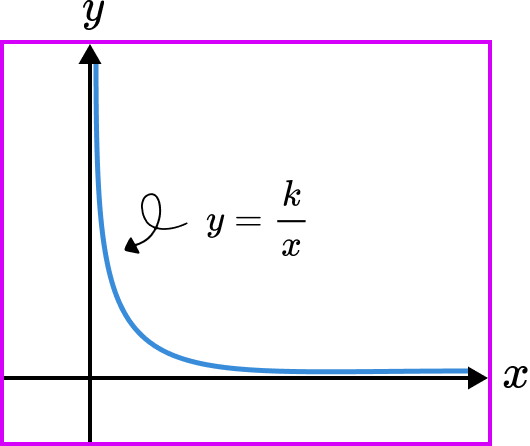
Note, the value of y can be inversely proportional to other powers of x including x^{2}, \ x^{3}, or even \sqrt{x}. Each of these has a different algebraic and graphical representation.
Step-by-step guide: Directly proportional graphs / inversely proportional graphs
How to use inverse proportion
In order to work out an unknown value given an inversely proportional relationship:
Write down the inverse proportion formula.
Determine the value of \textbf{k} .
Substitute \textbf{k} and the known value into the inverse proportion formula .
Solve the equation.
Explain how to use inverse proportion

Inverse proportion worksheet
Get your free inverse proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Inverse proportion examples
Example 1: complete the table y ∝ ⅟ x.
Given that y is inversely proportional to x, calculate the missing value of y in the table below.
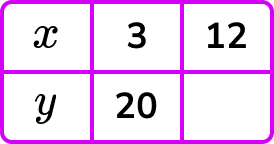
As y\propto\frac{1}{x}, we can write the formula y=\frac{k}{x}.
2 Determine the value of \textbf{k} .
Substituting a known pair of values (3,20), we can say,
3 Substitute \textbf{k} and the known value into the inverse proportion formula .
Now we have the equation y=\frac{60}{x}. Substituting x=12 into the equation to calculate the value for y, we have
y=\frac{60}{12} .
4 Solve the equation.
Dividing 60 by 12, we have y=5.
Notice that as the value for x increased, the value for y decreased.
Example 2: complete the table y ∝ ⅟ x
Let y\propto\frac{1}{x}. Calculate the value for x when y=20.
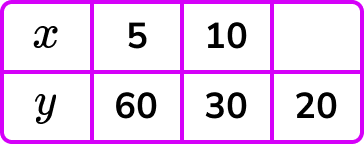
As y\propto\frac{1}{x} as stated in the question, we have
As x=5 when y=60, substituting these values into the formula, we get
\begin{aligned} 60&=\frac{k}{5}\\\\ 60\times{5}&=k\\\\ k&=300 \end{aligned}
Now we have y=\frac{300}{x}. We need to determine the value for x when y=20 and so, substituting this value into the equation, we get
20=\frac{300}{x} .
Example 3: complete the table y ∝ ⅟ x 2
Let y be inversely proportional to x^{2}. Calculate the missing value q.

As y\propto\frac{1}{x^{2}}, we have the formula y=\frac{k}{x^{2}}.
Using the table, we know that y=4 when x=2.
Note, we could also use the pair of values y=16 when x=1.
As y=\frac{k}{x^{2}}, substituting the values for y=4 and x=2, we have
\begin{aligned} 4&=\frac{k}{2^{2}}\\\\ 4&=\frac{k}{4}\\\\ 4\times{4}&=k\\\\ k&=16 \end{aligned}
Now we have y=\frac{16}{x^{2}}. We need to determine the value of y=q when x=4 and so, substituting these into the equation, we have
q=\frac{16}{4^{2}} .
Example 4: inverse proportion worded problem y ∝ ⅟ x
2 workers paint a fence in 9 hours.
How long would it take 6 workers to paint the same fence?
As the number of workers x increases, the time y taken to paint the same fence would decrease and so this is an inverse proportion of the form y\propto\frac{1}{x}.
This means that we have the formula y=\frac{k}{x}.
As we know x=2 when y=9, substituting these values into the formula, we get
\begin{aligned} 9&=\frac{k}{2}\\\\ 9\times{2}&=k\\\\ k&=18 \end{aligned}
Now we have the equation y=\frac{18}{x}. As we want to know the value for y when x=6, we substitute x=6 into the equation to get
y=\frac{18}{6} .
As 18 divided by 6 is equal to 3, we have the solution y=3.
Example 5: inverse proportion worded problem y ∝ ⅟ x 2
Let n represent the number of dogs and d represent the number of days. A bag of biscuits feeds 4 dogs for 12 days. Given that d\propto\frac{1}{n^{2}}, how many days would the same bag feed 5 dogs?
As d\propto\frac{1}{n^{2}} , we can state the inverse proportion formula,
d=\frac{k}{n^{2}}.
As d=12 when n=4, substituting these into the formula, we have
\begin{aligned} 12&=\frac{k}{4^{2}}\\\\ 12&=\frac{k}{16}\\\\ 12\times{16}&=k\\\\ k&=192 \end{aligned}
Now d=\frac{192}{n^{2}}. Now we have 5 dogs, we can substitute n=5 into the formula to calculate the number of days of food they have,
d=\frac{192}{5^{2}} .
Example 6: inverse proportion worded problem y ∝ ⅟ x 3
A cube of cheese has a density d=1.075\text{g/cm}^{3}. The side length of the cube is x=1.5cm. Another cube of cheese of the same mass has a density d=1.072\text{g/cm}^{3}.
What is the side length of the second cube of cheese? Write your answer to 3 decimal places.
The density of an object is equal to its mass divided by its volume.
In the case of the cheese the density d is inversely proportional to the cube of the side length x . d=\frac{k}{x^3} where k is the constant of proportionality.
k will represent the mass of the first cube of cheese.
As d=1.075 when x=1.5, substituting these values into the formula, we get
\begin{aligned} 1.075&=\frac{k}{1.5^{3}}\\\\ 1.075&=\frac{k}{3.375}\\\\ 1.075\times{3.375}&=k\\\\ k&=3.628125=\frac{1161}{320} \end{aligned}
This is the mass of the cheese in grams.
Now we have the equation d=\frac{3.628125}{x^{3}}. As the second cube has a density d=1.072\text{g/cm}^{3}, substituting this into the equation, we get
1.072=\frac{3.628125}{x^{3}} .
Common misconceptions
- Modelling assumption
Whenever you solve word problems for inverse proportion you assume that everything has the same rate. For example, if the question involves the number of people working, we assume all the workers work at the same rate.
- The constant of proportionality
For direct proportion, the constant of proportionality k is the ratio of the two variables such as k=y\div{x}. For inverse proportion, k is the product of the two variables, such as k=xy.
- The graph of an inversely proportional relationship does not cross either axis
The graph of any inversely proportional relationship cannot cross either axis. This is because, if we use the example y\propto\frac{1}{x}, if x=0, the value for y is undefined as we cannot divide a number by 0. If y=0, then the value for the constant of proportionality must be 0 or x=0, but as we have just said, x ≠ 0 and so the relationship between x and y cannot exist for these two values as k=0.
- Take care with writing time using the correct decimal
Time is used in some inverse proportion word problems. If an answer is 3.1 you may be tempted to write it as 3 hours 10 minutes, but it would be 3 hours 6 minutes. (Remember there are 60 minutes in an hour).
- Graphs of the reciprocal function
The standard graph for y\propto{x} is a straight line graph that passes through the origin with the gradient k. The standard graph for y\propto\frac{1}{x} is a curved line that does not cross either axis.
Related lessons on inverse proportion
Inverse proportion is part of our series of lessons to support revision on proportion . You may find it helpful to start with the main proportion lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
- Direct and indirect proportion
- Direct proportion formula
Practice inverse proportion questions
1. As y is inversely proportional to x, complete the table by calculating the missing value for y.
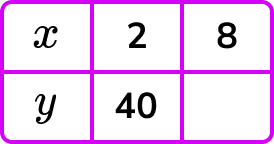
y=\frac{k}{x} and so k=xy.
When x=8, \ y=\frac{80}{8}=10 .
2. Given that n is inversely proportional to the square of m, calculate the positive value for m when n=8.
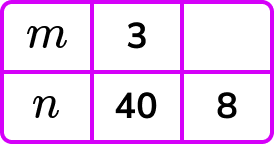
n=\frac{k}{m^2} and so k=m^{2} n.
When n=8, \ m^2=\frac{360}{8}=45
3. Let b be inversely proportional to \sqrt{a}. Calculate the value for b when a=25.

b=\frac{k}{\sqrt{a}} and so k=b\sqrt{a}.
When a=25, \ b=\frac{10}{\sqrt{25}}=\frac{10}{5}=2 .
4. 20 people take 36 days to build a house. How many days would it take 60 people to build the same house?
Let p represent the number of people and d represent the number of days of building, then
d=\frac{k}{p} and so k=dp.
When p=60, \ d=\frac{720}{60}=12.
5. A bike travelling at 8 \ km/h completes a journey in 40 minutes. How long would the same journey take if the speed was increased to 16 \ km/h?
Let s represent speed and t represent time taken, then
s=\frac{k}{t} and so k=st.
Note, the speed-distance-time formula is a known relationship (speed = distance \div time). For a constant distance, if the time taken to reach the destination increases, the speed must have decreased, or vice versa.
6. A fudge company works out that the cost of making a bag of fudge (c) decreases as the number of bags produced (b) increases. If c\propto\frac{1}{b^{2}} and producing 12 bags of fudge costs £2.70 each to make, how many bags of fudge can be made for £1.50 each?
We have c=\frac{k}{b^{2}} and so k=b^{2}c.
When c=1.5,
Inverse proportion GCSE questions
1. Let y be inversely proportional to the square of x.
Complete the table.

y=\frac{72}{x^{2}} or y=72\div{2^{2}} or y=72\div{12^{2}}
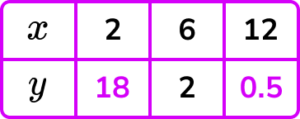
2. It takes 6 workers 24 hours to build an emergency flood barrier.
The wall needs to be built in 8 hours.
How many workers are needed to build the same emergency flood barrier in 8 hours?
3. It takes 360 minutes to fill a swimming pool from 5 taps.
(a) How many minutes would it take 3 taps to fill the swimming pool?
(b) State one assumption you made in working out your answer to part (a).
1800 \div 3=600 minutes
All taps work at the same rate.
Learning checklist
You have now learned how to:
- Solve problems involving inverse proportion, including algebraic representations
The next lessons are
- Compound measures
- Best buy maths
- Scale maths
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.
Privacy Overview

Inverse Proportion – Examples and Practice Problems
Proportionality is a way of relating two quantities. In the case of inverse proportion, the relationship is such that, if we increase one quantity, the other quantity decreases and vice versa. Here, we will look at a brief summary of inverse proportion.
Then, we will look at examples with answers to understand the use of inverse proportion with real problems.

Relevant for …
Exploring examples with answers of inverse proportion.
See examples
Summary of inverse proportion
Inverse proportion – examples with answers, inverse proportion – practice problems.
Unlike direct proportion, where one quantity varies directly as another quantity varies, in inverse proportion, an increase in one variable causes a decrease in the other variable and vice versa. If the variable a is inversely proportional to the variable b , then this can be represented with the formula:
$latex a \propto \frac{1}{b}$
If we change the sign of proportionality to the equal sign, we have the equation:
$latex ab=k$
where k is the constant of proportionality.
To find an inverse proportion equation, we have to start by finding the proportional relationship. Next, we write the equation using the constant of proportionality. Then, we find the value of the constant using the given values , and finally, we plug the value of the constant into the equation.
There are several situations in everyday life that have inverse proportion relationships, for example:
• The time taken by a certain number of workers to complete a job varies inversely with the number of workers. This means that the more workers we have, the less time it will take to complete the job and vice versa.
• The speed of different means of transport such as a car, a train, an airplane varies inversely with the time taken to travel a certain distance. The faster the speed, the less time it will take to cover a certain distance.
The following inverse proportion examples have their respective solution. You can use these examples to fully understand the concepts in this topic. For better practice, you can solve the exercises yourself before looking at the answers.
If it takes 20 workers 8 days to harvest coffee on a plantation. How long would it take 16 workers to harvest the same plantation?
From the question, we have that 20 workers take 8 days. This means that one worker will take:
1 worker $latex=(20\times 8)$ days
Now, we calculate the time it will take for 16 workers:
16 workers $latex =\frac{20\times 8}{16}$ days
$latex =10$ days
Thus, 16 workers will take 10 days.
9 taps can fill a tank in 4 hours. How long would it take to fill the same tank if we have 12 taps with the same water flow?
It takes 9 taps 4 hours and we have to find the time it takes 12 taps. Therefore, we can form the following relationship:
$latex \frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}$
⇒ $latex \frac{9}{x}=\frac{12}{4}$
⇒ $latex x=3$
Thus, it will take 12 taps 3 hours to fill the tank.
4 people can unload a truck full of rice in 3 hours. How long would it take 7 people to unload the same truck?
We have that 4 people would take 3 hours. This means that one person will take:
1 person $latex=(4\times 3)$ hours
Now, we calculate the time it will take 7 people:
7 people $latex =\frac{4\times 3}{7}$ hours
$latex =\frac{12}{7}$ hours
Thus, 7 people will take $latex \frac{12}{7}$ hours or 1.71 hours.
A military base had supplies for 300 soldiers for 90 days. After 20 days, 50 soldiers left the base. How long will the food last?
After 20 days, the number of soldiers left on the base is:
soldiers $latex=(300-50)=250$
After 20 days, the number of days that supplies would last for the 300 military personnel is:
days $latex =(90-20)=70$
Thus, 300 soldiers had supplies for 70 days. This means that 1 soldier had provisions for:
1 soldier $latex =(300\times 70)$ days
250 soldiers $latex =\frac{300\times 70}{250}$ days
$latex =84$ days
Therefore, the remaining provisions will last 84 days for 250 soldiers.
6 writers who work 5 hours a day can transcribe a book in 16 days. How many days will it take 4 writers to transcribe the same book, each working 6 hours a day?
We have that 6 writers who work 5 hours a day can finish the job in 16 days. This means that 6 writers working 1 hour a day can finish it in:
6 writers 1 hour a day $latex =(16\times 5)$ days
1 writer who works 1 hour a day can finish it in:
1 writer 1 hour daily $latex =(16\times 5\times 6)$ days
1 writer working 6 hours a day can finish it in:
1 writer 6 hours a day $latex =\frac{16\times 5\times 6}{6}$ days
4 writers working 6 hours a day can end up in:
1 writer 6 hours a day $latex =\frac{16\times 5\times 6}{6\times 4}$ days
$latex =20$ days
Therefore, 4 writers working 6 hours a day can finish the job in 20 days.
In a toy factory, 36 machines are required to produce a certain number of toys in 54 days. How many machines does it take to produce the same number of toys in 81 days?
We can form a table with the given data:
| 36 | x | |
| 54 | 81 |
Now, we can form the following equation and solve:
$latex 36\times 54=x\times 81$
$latex \frac{36\times 54}{81}=x$
$latex \frac{4\times 54}{9}=x$
$latex x=\frac{216}{9}$
$latex x=24$
Therefore, it takes 24 machines to produce the same number of toys in 81 days.
After carefully reviewing the examples solved above, you can solve the following problems to test your knowledge of inverse proportion. Select an answer and check it to see if you chose the correct answer.
If 35 workers can finish a task in 8 days, how many days will it take 20 workers to complete the same task?
Choose an answer
A military base has enough food to feed 80 soldiers for 60 days. Calculate how many days the meal will last if 20 soldiers join the base after 15 days
A scientific investigation takes 125 days to complete if 16 scientists work on it. how many scientists does it take to complete the investigation in 40 days, if a box of pencils is distributed among 25 children, each child will receive 2 pencils. how many pencils will each child receive if the number of children is reduced by 10.
Interested in learning more about proportionality? Take a look at these pages:
- Direct and Inverse Proportionality
- Examples of Direct Proportion
- Examples of Compound Proportion

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.
INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author
Inverse Variation
Inverse Variation or Inverse Proportion:
Two quantities are said to vary inversely the increase (or decrease) in one quantity causes the decrease (or increase) in the other quantity.
Examples on Inverse Variation or Inverse Proportion:
(i) The time taken to finish a piece of work varies inversely as the number of men at work. (More men at work, less is the time taken to finish it)
(ii) The speed varies inversely as the time taken to cover a distance. (More is the speed, less is the time taken to cover a distance)
Solved worked-out problems on Inverse Variation:
1. If 35 men can reap a field in 8 days; in how many days can 20 men reap the same field? Solution: 35 men can reap the field in 8 days 1 man can reap the field in (35 × 8) days [less men, more days] 20 men can reap the field in (35 × 8)/20 days [more men, more days] = 14 days Hence, 20 men can reap the field in 14 days.
2. A fort had provisions for 300 men for 90 days. After 20 days, 50 men left the fort. How long would the food last at the same rate? Solution: Remaining number of men = (300 - 50) = 250. Remaining number of days = (90 - 20) days = 70 days. 300 men had provisions for 70 days 1 man had provisions for (300 × 70) days [less men, more days] 250 men had provisions for (300 × 70)/250 days [more men, more days] = 84 days. Hence, the remaining food will last for 84 days.
More examples on Inverse Variation word problems:
3. 6 oxen or 8 cows can graze a field in 28 days. How long would 9 oxen and 2 cows take to graze the same field? Solution: 6 oxen = 8 cows ⇒ 1 ox = 8/6 cows ⇒ 9 oxen ≡ (8/6 × 9) cows = 12 cows ⇒ (9 oxen + 2 cows) ≡ (12 cows + 2 cows) = 14 cows Now, 8 cows can graze the field in 28 days 1 cow can graze the field in (28 × 8) days [less cows, more days] 14 cows can graze the field in (28 × 8)/14 days [more cows, less days] = 16 days Hence, 9 oxen and 2 cows can graze the field in 16 days.
4. 6 typists working 5 hours a day can type the manuscript of a book in 16 days. How many days will 4 typists take to do the same job, each working 6 hours a day? Solution: 6 typists working 5 hours a day can finish the job in 16 days 6 typists working 1 hour a day can finish it in (16 × 5) days [less hours per day, more days] 1 typist working 1 hour a day can finish it in (16 × 5 x 6)/6 days [less typists, more days] 1 typist working 6 hours a day can finish it in 6 days [more hours per day, less days] 4 typists working 6 hours a day can finish it (16 × 5 × 6)/(6 × 4) days
= 20 days. Hence, 4 typists working 6 hours a day can finish the job in 20 days.
● Ratio and Proportion (Direct & Inverse Variation)
Direct Variation
Practice Test on Direct Variation and Inverse Variation
● Ratio and Proportion - Worksheets
Worksheet on Direct Variation
Worksheet on Inverse Variation
8th Grade Math Practice
From Inverse Variation to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
5th grade math problems | table of contents | worksheets |free answers.
Aug 19, 24 02:00 AM
Construction of Perpendicular Lines by Using a Protractor, Set-square
Aug 18, 24 02:47 PM

Constructing a Line Segment |Construction of Line Segment|Constructing
Aug 16, 24 04:35 PM

Construction of a Circle | Working Rules | Step-by-step Explanation |
Aug 13, 24 01:27 AM
Practical Geometry | Ruler | Set-Squares | Protractor |Compass|Divider
Aug 12, 24 03:20 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Direct and Inverse Proportion: Worksheets with Answers
Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all (well, most!) come with answers.
Mathster keyboard_arrow_up Back to Top
Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers.
| Worksheet Name | 1 | 2 | 3 |
|---|---|---|---|
| Direct Proportionality - Basics | |||
| Direct Proportionality – Advanced | |||
| Inverse Proportionality – Basics | |||
| Inverse Proportionality - Advanced | |||
| Proportionality - Direct and Inverse |
Corbett Maths keyboard_arrow_up Back to Top
Corbett Maths offers outstanding, original exam style questions on any topic, as well as videos, past papers and 5-a-day. It really is one of the very best websites around.
| Name | Questions | Solutions |
|---|---|---|
| Proportion: direct | ||
| Proportion: inverse |
Inverse Proportion
Inverse proportion is when two quantities change opposite to one another.
As one quantity increases, the other quantity decreases. When the two quantities are multiplied, the same constant occurs .
A common example of inverse proportion is to calculate the time it takes to do a job with more or fewer workers.
Example One - Painting a Wall Mural

3 talented graffiti artists can paint a wall mural in 10 hours. To paint the same mural on another wall, calculate the time it would take: (a) 1 artist (b) 6 artists.
Answer: (a) Multiplied constant = 3 artists × 10 hours = 30 man-hours
Time with 1 artist = 30 man-hours ÷ 1 artist = 30 hours
(b) Time with 6 artists = 30 man-hours ÷ 6 artists = 5 hours
Example Two - Building a Shed
4 men can build a shed in 20 hours. Calculate how long the same shed would take to build: (a) if there was 1 man (b) if there were 5 men.
Answer: (a) Multiplied constant = 4 men × 20 hours = 80 man-hours
Time with 1 man = 80 man-hours ÷ 1 man = 80 hours
(b) Time with 5 men = 80 man-hours ÷ 5 men = 16 hours
Question - Building a Fence
It takes 6 people 8 hours to build a fence around a farm. How long would the same fence have taken to build with 12 people? (Hint: Find the number of hours with only 1 person first.)
Answer 4 hours
Maths Fun - BMI (Body Mass Index)
Doctors use a Body Mass Index to determine if people are healthy or not. A BMI of 25 is healthy. Less than 25 is underweight. More than 25 is overweight.
| Body Mass Index = | Mass in kg |
| Height in metres-squared |
Measure your mass in kilograms. Measure your height in metres. Calculate your BMI. According to the rule above, are you healthy? What problems are there with this rule?
Measurement
Probability
Xcelerate Math
Xcelerate Math on youtube
Xcelerate Science
Qld Science Teachers
Copyright © 2012-2023 Xcelerate Math
Directly Proportional and Inversely Proportional

Directly proportional: as one amount increases, another amount increases at the same rate.
| ∝ | The symbol for "directly proportional" is ∝ (Don't confuse it with the symbol for ∞) |
Example: you are paid $20 an hour
How much you earn is directly proportional to how many hours you work
Work more hours, get more pay; in direct proportion.
This could be written:
Earnings ∝ Hours worked
- If you work 2 hours you get paid $40
- If you work 3 hours you get paid $60
Constant of Proportionality
The "constant of proportionality" is the value that relates the two amounts
Example: you are paid $20 an hour (continued)
The constant of proportionality is 20 because:
Earnings = 20 × Hours worked
This can be written:
Where k is the constant of proportionality
Example: y is directly proportional to x, and when x=3 then y=15. What is the constant of proportionality?
They are directly proportional, so:
Put in what we know (y=15 and x=3):
Solve (by dividing both sides by 3):
The constant of proportionality is 5:
When we know the constant of proportionality we can then answer other questions
Example: (continued)
What is the value of y when x = 9?
What is the value of x when y = 2?
Inversely Proportional
| Proportional: when one value at the same rate that the other . |
Example: speed and travel time
Speed and travel time are Inversely Proportional because the faster we go the shorter the time.
- As speed goes up, travel time goes down
- And as speed goes down, travel time goes up

Example: 4 people can paint a fence in 3 hours. How long will it take 6 people to paint it? (Assume everyone works at the same rate)
It is an Inverse Proportion:
- As the number of people goes up, the painting time goes down.
- As the number of people goes down, the painting time goes up.
We can use:
- t = number of hours
- k = constant of proportionality
- n = number of people
"4 people can paint a fence in 3 hours" means that t = 3 when n = 4
So now we know:
And when n = 6:
So 6 people will take 2 hours to paint the fence.
How many people are needed to complete the job in half an hour?
So it needs 24 people to complete the job in half an hour. (Assuming they don't all get in each other's way!)
Proportional to ...
It is also possible to be proportional to a square, a cube, an exponential, or other function!
Example: Proportional to x 2

A stone is dropped from the top of a high tower.
The distance it falls is proportional to the square of the time of fall.
The stone falls 19.6 m after 2 seconds, how far does it fall after 3 seconds?
- d is the distance fallen and
- t is the time of fall
When d = 19.6 then t = 2
And when t = 3:
So it has fallen 44.1 m after 3 seconds.
Inverse Square
Inverse Square : when one value decreases as the square of the other value.
Example: light and distance
The further away we are from a light, the less bright it is.
In fact the brightness decreases as the square of the distance. Because the light is spreading out in all directions.
So a brightness of "1" at 1 meter is only "0.25" at 2 meters (double the distance leads to a quarter of the brightness), and so on.

Inverse Proportion Video
GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
Helping with Math
Inverse Proportion
Introduction
We frequently come into situations in our daily lives when the change in values of one quantity is affected by the change in values of another quantity. Two quantities can be related through proportionality. A change in one quantity’s proportion could sometimes result in a change in the proportion of another. Let us say, for instance, that if we drive faster, it takes less time to travel a certain distance. This scenario shows inverse proportionality between two quantities.
The definition of inverse proportion, how it differs from direct proportion , real-life applications, and various examples of inverse proportion will all be covered in this article.
What is Inverse Proportion?
Inverse proportion refers to the relationship between two quantities if an increase in one causes a decrease in the other and a decrease in one causes an increase in the other. In other terms, two quantities are said to be in inverse proportion if their product is equal to a constant value regardless of changes in their values.
They are said to be in inverse proportion when one quantity increases while the other decreases and vice versa. Let’s examine the table below to provide an example of inverse proportion.
| 2 | 32 |
| 4 | 16 |
| 8 | 8 |
| 16 | 4 |
| 32 | 2 |
| 64 | 1 |
Let us find out how the numbers show an inverse proportion by getting the product of each row. The table third column, ab, shows that the product of a and b are the same.
| 2 | 32 | 2×32=64 |
| 4 | 16 | 4×16=64 |
| 8 | 8 | 8×8=64 |
| 16 | 4 | 16×4=64 |
| 32 | 2 | 32×2=64 |
| 64 | 1 | 64×1=64 |
We can say that the numbers in columns a and b as “ a is inversely proportional to b” or may be represented as a∝b. Let us use the equation below to calculate the other values.
a=$\frac{64}{b}$
When b=32, a=$\frac{64}{32}$=2.
When b=16, a=$\frac{64}{16}$=4.
When b=8, a=$\frac{64}{32}$=8.
When b=4, a=$\frac{64}{4}$=16.
When b=2, a=$\frac{64}{2}$=32.
When b=1, a=$\frac{64}{1}$=64.
Formula: Inverse Proportion
The inverse proportion formula can determine a relationship between two inversely proportional quantities. Assume that x decreases when y increases and vice versa for the two values, x and y.
As an illustration, consider the relationship between speed and time. With increasing speed, it takes less time for us to cover a certain distance.
Time travel decreases as speed increases. Time travel increases as speed decreases.
The relationship between speed and time, denoted as y and x, can be expressed mathematically as the inverse proportion formula.
Written as follows is the inverse proportional formula:
y=$\frac{k}{x}$
Take note of the following:
k is the constant of proportionality As x decreases, y increases. As x increases, y decreases.
The formulas below also show inverse proportionality.
y∝$\frac{1}{x}$; y=k⋅$\frac{1}{x}$; y=k ($\frac{1}{x}$)
The proportional relationship between two quantities is indicated here by the symbol .
Real World Examples of Inverse Proportion
Among the many inverse proportions scenarios are the following examples:
( 1 ) A moving object’s speed, such as a moving train, car, or ship, inversely varies with the time necessary to travel a specific distance. Less time is needed to complete a distance as speed increases.
As speed increases , time travel decreases . As speed decreases , time travel increases .
( 2 )The number of people or workers present at work is inversely proportional to the amount of time it takes for a given number of people or workers to perform a task. This implies that the length of time it takes to complete the work increases with the number of workers and vice versa.
As the number of people or workers increases , the time it takes to finish a task decreases. As the number of people or workers decreases , the time it takes to finish a task increases.
( 3 ) The distance between you and an ambulance as it is approaching impacts how loud its siren will be. As the ambulance approaches you, the siren becomes louder, and as it moves away, it gets quieter. The siren gets louder and quieter depending on how far away you are from the ambulance. The louder the siren, the closer you are.
As the distance between you and an ambulance increases , the sound of the siren decreases . As the distance between you and an ambulance decreases , the sound of the siren increases .
( 4 ) The brightness of a streetlight has an inverse relationship with the distance between you and it. This indicates that the streetlight’s brightness decreases as you get farther away. The streetlight will typically be brighter if you are 50 meters from it than if you are 200 meters away.
As the distance between you and the streetlight increases, its brightness decreases. As the distance between you and the streetlight decreases, its brightness increases.
( 5 ) The number of goods you can buy is inversely related to the price of each item. Suppose you were to consider your spending limit when purchasing some apples from the market. If the price of each apple is \$0.50 instead of \$0.75, you can buy more apples.
( 6 ) A device’s battery life is inversely proportional to the amount of time it is utilized. Consider charging a device, let us say for example a laptop, to 95% before using it. Let us suppose that after an hour of use, the battery lowers to 85%, after two hours, it reduces to 77%. A considerable and proportional decline in the battery percentage may be immediately detected with an increase in the amount of time that the device is being utilized.
Aside from the listed above, there are more examples of scenarios that involve inverse proportion. Remember that when two things are said to be in inverse proportion, a change in one quantity corresponds to a corresponding decrease or increase in the other. If we know essential information pertaining to the problem statement, the concept of inverse proportion makes it easy for us to calculate the amount or value of a missing entity.
Direct vs Inverse Proportion
Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality. Let us say, for example, the variable x and y; if y is proportional to x, then it is represented as y∝x. If we have y is inversely proportional to x, then it is represented as y∝$\frac{1}{x}$. Now in both instances, the value of “y” changes in relation to “x,” or the value of “x” changes in relation to “y”. A proportionality constant is equivalent to the change in both values.
Direct Proportion
When y∝x, two variables x and y are said to be in direct proportion. This suggests that, for a constant k, y = kx. The ratio of two variables in a direct variation relationship is equal for all values.
When y∝1/x, two variables, x and y, are said to be in inverse proportion. This means that, for a constant k, y = k/x. The product of two variables in an inverse proportion relationship is equal for all values.
To visualize the difference between direct and inverse proportion, look at the illustration below.
For the graph of directly proportional, it shows that as the value of x increases, the value of y increases also. We may also say that as y decreases, x also decreases. On the other hand, for the graph inversely proportional, as the value of x increases, the value of y decreases or when x decreases, the value of y increases.
Graph of Inverse Proportion
The graph below shows that the quantities are in inverse proportion. It shows the relationship between the x and y values. It reads as y is inversely proportional to x.
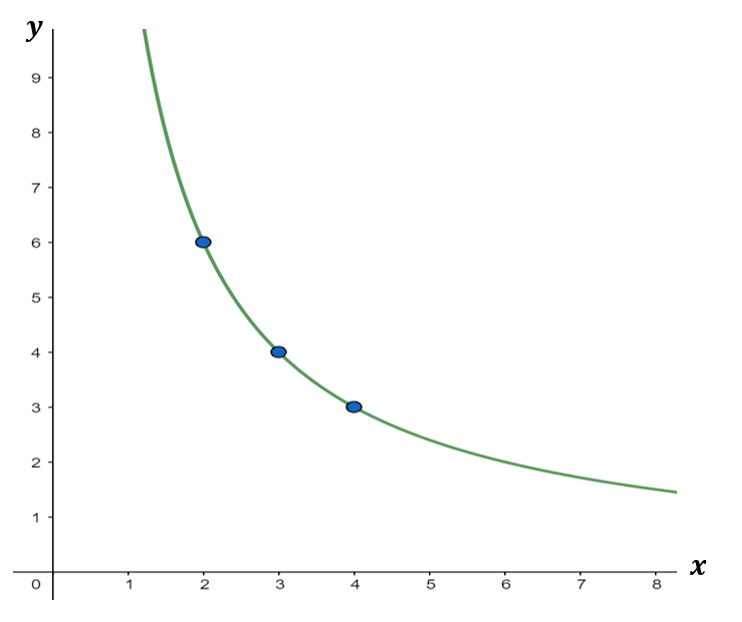
Using the graph above, let us identify some points and arrange them in a table.
| x | 2 | 3 | 4 |
| y | 6 | 4 | 3 |
Let us say that Point A has the coordinates ( 2, 6 ), Point B has the coordinates ( 3, 4 ), and Point C has the coordinates ( 4, 3 ).
By the inverse proportion formula, let us check if the graph indeed shows an inverse proportion.
| Point A: ( 2, 6 ) y=$\frac{k}{x}$ 6=$\frac{k}{2}$ 6⋅2=k 12=k k=12 | Point B ( 3, 4 ) y=$\frac{k}{x}$ 4=$\frac{k}{3}$ 4⋅3=k 12=k k=12 | Point C ( 4, 3 ) y=$\frac{k}{x}$ 3=$\frac{k}{4}$ 3⋅4=k 12=k k=12 |
Since the product of x and y is constant, the given data shows inverse proportionality with an equation y=$\frac{12}{x}$. Thus, if we want to find the values of x given y or vice versa, we can easily identify them. For example,
| when x=6 y=$\frac{12}{x}$ y=$\frac{12}{x}$ y=2 | when y=18 y=$\frac{12}{x}$ 18=$\frac{12}{x}$ x=$\frac{12}{18}$ x=23 |
Therefore, the other coordinates on the graph are ( 6, 2 ) and ( $\frac{2}{3}$, 18 ).
How Should I Write Indirect Proportion Equations?
The steps listed here should be followed when writing an inverse proportion equation.
1. Find the constant of proportionality.
2. Enter the proportionality constant into an equation after finding it.
Let us use the table below as an example and figure out its inverse proportion equation.
| x | 50 | 25 | 20 |
| y | 2 | 4 | 5 |
Using the steps mentioned above, let us write the indirect proportion equation of the given data.
Since the formula for indirect proportion is y=$\frac{k}{x}$, where k is the constant of proportionality, we will have,
| 2=$\frac{k}{50}$ 2⋅50=k 100=k k=100 | 4=$\frac{k}{25}$ 4⋅25=k 100=k k=100 | 5=$\frac{k}{20}$ 5⋅20=k 100=k k=100 |
The given data indeed shows an inverse proportion since the product of the shared x and y values is constant.
The proportion equation of the data given is:
y=$\frac{100}{x}$
Knowing the indirect proportion equation will help us to identify unknown values. For example, if y=10, then x must be equal to 10.
More Examples
Assume that 4 people work at the same rate in painting a fence for 6 hours.
( a ) How long will it take 8 people to paint the fence?
( b ) How long will it take 12 people to paint the fence?
( c ) How many people are needed to complete the task in 30 minutes?
This scenario shows an inverse proportion since. The painting time will go down if the number of people goes up. Let us use the inverse proportion equation,
where y is the number of hours spent painting the fence, x is the number of people working, and k is the constant of proportionality.
Since 4 people can paint the fence in 6 hours, we have x=4 and y=6. Plugging in these values in the equation, we have,
6=$\frac{k}{4}$ 6⋅4=k 24=k k=24
Now that we already know the constant of proportionality, which is 24, we now have the equation,
y=$\frac{24}{x}$
Let us plug in 8 to the value of x in the equation.
y=$\frac{24}{8}$ y=3
Therefore, it will take 3 hours for 8 people to paint the fence.
Plugging in x=12 to the inverse proportion equation we have,
y=$\frac{24}{12}$ y=2
Hence, 12 people can finish painting the fence in 2 hours.
In this question, we will use ½ or 0.5 hours since it is equivalent to 30 minutes. This time y=½, and we are solving for x.
Substituting ½ in the equation,
12=$\frac{24}{x}$ x=24⋅2 x=48
Thus, 48 people are needed to finish the task in 30 minutes.
The value p is inversely proportional to r. If p=40 and r=2,
( a ) Find the equation relating the given data. ( b ) If p=20, what is r? ( c ) If r=5, find p.
( a ) Find the equation relating the given data.
The statement p is inversely proportional to r is written as,
p∝$\frac{1}{r}$
To find the equation relating p and r, let us use the formula p=kr to identify the constant of proportionality.
p=$\frac{k}{r}$ 40=$\frac{k}{2}$ 40⋅2=k 80=k k=80
Since we already know that 80 is the constant of proportionality, we have the equation,
p=$\frac{80}{r}$
( b ) If p=20 , what is r?
Let us substitute the given value of p to the inverse proportion equation.
p=$\frac{80}{r}$ 20=$\frac{80}{r}$ r=$\frac{80}{20}$ r=4
Therefore, the value of r is equal to 4 when p is 20.
( c ) If r=5, find p.
This time, r is given, and we must find the value of p.
p=$\frac{80}{5}$ p=16
Hence, when r=5, the value of p is 16.
Suppose it takes 3 students to finish a project in 6 hours. When 9 students are working on the same project, how long does it take to complete the task?
Let x=number of students and y=hours spent doing the project.
Let us first find the constant of proportionality. Thus, we have
y=$\frac{k}{x}$ 6=$\frac{k}{3}$ 6⋅3=k 18=k k=18
Hence, the inverse proportion equation to represent the scenario is,
y=$\frac{18}{x}$
Since k=18, let us now solve for hours spent in doing the project if 9 students will be working on it.
y=$\frac{k}{9}$ y=2
Therefore, it will take 2 hours to finish the project by 9 students.
Suppose the table below shows an inverse proportion.
| x | 5 | 4 | 3 | |
| y | 10 | 12 | 20 |
( a ) Find the constant of proportionality ( b ) Write the equation of inverse proportion ( c ) Complete the table.
The table has given the values for x and y. Since they are inversely proportional, we may have the equation,
( a ) Find the constant of proportionality
Let us find the constant of proportionality from the table where both x and y are given.
| y=$\frac{k}{x}$ 12=$\frac{k}{5}$ 12⋅5=k 60=k k=60 | y=$\frac{k}{x}$ 20=$\frac{k}{3}$ 20⋅3=k 60=k k=60 |
Hence, the constant of proportionality is 60.
( b ) Write the equation of inverse proportion.
By substituting the computed constant of proportionality, the equation is,
( c ) Complete the table.
Here is the complete table.
| x | 5 | 4 | 3 | |
| y | 10 | 12 | 15 | 20 |
y=$\frac{60}{x}$ 10=$\frac{60}{x}$ x=$\frac{60}{10}$ x=6
y=$\frac{60}{x}$ y=$\frac{60}{4}$ x=15
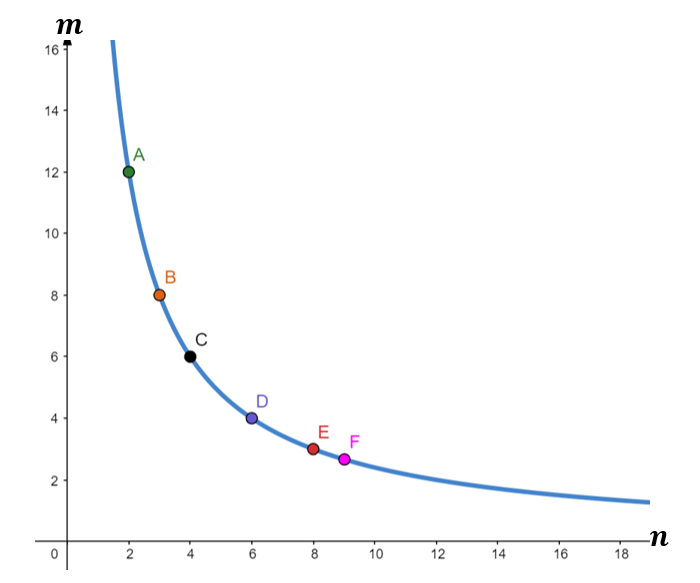
m is inversely proportional to n. When m=4, n=6.
Draw the graph after filling out the values in the table below.
| n | 2 | 3 | 4 | 6 | 8 | 9 |
| m | 6 |
Since m is inversely proportional to n, in symbols, it is written as m∝$\frac{1}{n}$.
Let us use the given values of n and m to find the constant of proportionality. Hence, we will use the formula,
m=$\frac{k}{n}$
Substituting the given values, we have,
Knowing the value of the constant of proportionality makes it easy to complete the data.
We will now utilize the equation m=$\frac{24}{n}$.
| when n=2 m=$\frac{24}{n}$ m=$\frac{24}{2}$ m=12 | when n=3 m=$\frac{24}{n}$ m=$\frac{24}{3}$ m=8 | when n=6 m=$\frac{24}{n}$ m=$\frac{24}{6}$ m=4 |
| when n=8 m=$\frac{24}{n}$ m=$\frac{24}{8}$ m=3 | when n=9 m=$\frac{24}{n}$ m=$\frac{24}{9}$ m=$\frac{8}{3}$ |
The table below shows the completed data.
| n | 2 | 3 | 4 | 6 | 8 | 9 |
| m | 12 | 8 | 6 | 4 | 3 | $\frac{8}{3}$ |
Let us write each pair as coordinates of points A, B, C, D, E, and F. Hence, we may have,
Point A ( 2, 12 )
Point B ( 3, 8 )
Point C ( 4, 6 )
Point D ( 6, 4 )
Point E ( 8, 3 )
Point F ( 9, $\frac{8}{3}$ )
The figure below shows the graph of m=$\frac{24}{n}$.
Definition: Two quantities are said to be in inverse proportion when one quantity increases while the other decreases and vice versa.
Formula:
How do I Write inverse proportion Equations?
1. Find the constant of proportionality. 2. Enter the proportionality constant into an equation after finding it.
Frequently Asked Questions on Inverse Proportion (FAQs)
What is meant by inverse proportion.
One kind of proportionality relationship is inverse proportion. There is an inverse proportionality in two quantities when one quantity’s value increases relative to a decrease in another or vice versa.
Other names for inverse proportion include indirect proportion and inverse variation. Examples of inverse proportion include the amount of time it takes to travel a certain distance lowers as our speed rises, and the time it takes to finish a task decreases as more people work on it.
How do the inverse and direct proportions differ from one another?
Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality.
y∝x is read as “y is directly proportional to x”. y∝$\frac{1}{x}$ is read as “y is inversely proportional to x”.
What is the equation for inverse proportion?
The equation for inverse proportion is y=$\frac{k}{x}$ or xy=k, where k is the constant of proportionality. You can use the known values to get the value of the constant k and then apply this formula to determine all the other unknown values.
How do you find the value of “k” in an inverse proportion?
The variable “k” is the constant of proportionality. In inverse proportion, we follow the formula y=$\frac{k}{x}$ when y is inversely proportional to x. Hence, to find the value of “k”, you must get the product of the given values of x and y.
Let us say, for instance, that y is inversely proportional to x, and we know that x=5 and y=6. Here is how to find the constant of proportionality, “k”.
k=xy k=5⋅6 k=30
Hence, the constant of proportionality for the inverse proportion is 30. The equation that represents the given value is,
y=$\frac{30}{x}$
Finding the value of the constant of proportionality is very helpful for solving the equation for the inverse proportion and for determining other values. Therefore, we can readily determine y as 3 or 2, respectively, if x is 10 or 15.
Recommended Worksheets
Inverse Proportion (Summer Themed) Math Worksheets Direct Proportion (Labor Day Themed) Math Worksheets Proportion (Thanksgiving Day Themed) Math Worksheets
Link/Reference Us
We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!
<a href="https://helpingwithmath.com/inverse-proportion/">Inverse Proportion</a>
"Inverse Proportion". Helping with Math . Accessed on August 19, 2024. https://helpingwithmath.com/inverse-proportion/.
"Inverse Proportion". Helping with Math , https://helpingwithmath.com/inverse-proportion/. Accessed 19 August, 2024.
Additional Numbers Theory:
Latest worksheets.
The worksheets below are the mostly recently added to the site.
August Free Bundle of Worksheets

Multiplying Mixed Numbers by Fractions 5th Grade Math Worksheets

Dividing Mixed Numbers by Fractions 5th Grade Math Worksheets

July Free Bundle of Worksheets

Grade 1 Geometry Free Bundle

Grade 1 Measurement and Data Free Bundle


Grade 1 Operations and Algebraic Thinking Free Bundle

Grade 1 Number and Operations in Base Ten Free Bundle

June Free Bundle of Worksheets

Comparing Data Using “Less” and “More” 1st Grade Math Worksheets

Inverse Proportion
When two quantities are related to each other inversely, i.e., when an increase in one quantity brings a decrease in the other and vice versa then they are said to be in inverse proportion. In inverse proportion, the product of the given two quantities is equal to a constant value. Let's learn more about it in detail in this article.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What is Inverse Proportion?
The definition of inverse proportion states that "Two quantities are said to be in inverse proportion if an increase in one leads to a decrease in the other quantity and a decrease in one leads to an increase in the other quantity". In other words, if the product of both the quantities, irrespective of a change in their values, is equal to a constant value, then they are said to be in inverse proportion . For example, let us take the number of workers and the number of days required by them to complete a given amount of work as x and y respectively.
| Numbers of Workers (x) | Number of Days Required (y) |
|---|---|
| 16 | 3 |
| 12 | 4 |
| 8 | 6 |
| 4 | 12 |
Are the number of workers and the number of days in inverse proportional relation? Let's find out.
Observe the values written in the table carefully. You will find out that for each row, the product of x and y are the same. That means if there are 16 workers, they will complete the work in 3 days. So, here x × y = 16 × 3 = 48. Now, we decrease the number of workers, it is obvious that the less number of workers will do the same work in more time. But we see the product of x and y here, it is 12 × 4 = 48. Again, for 8 workers in 6 days, the product is 48. And same for 4 workers in 12 days. So, the product of two quantities in inverse proportion is always equal.
Inverse Proportion Formula
Inverse proportion formula help in establishing a relationship between two inversely proportional quantities. Let x and y be two quantities and assume that x is decreasing when y is increasing and vice versa. Example: The speed is inversely proportional to the time. As the speed increases, the time taken by us to cover the same distance decreases. Taking speed as y and time as x, we can say that y is said to be inversely proportional to x and is written mathematically as inverse proportion formula.
The inverse proportional formula is written as
- k is the constant of proportionality .
- y increases as x decreases.
- y decreases as x increases.
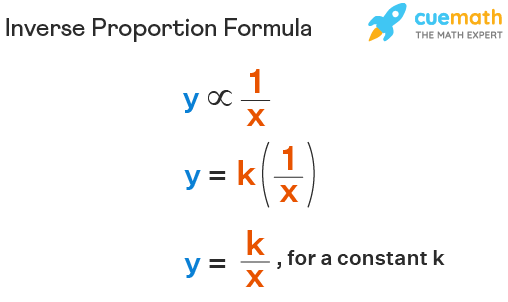
Here the symbol ∝ denotes the proportional relationship between two quantities.
Inverse Proportion Graph
The graph of inverse proportion is usually a curve that bends towards the origin forming the shape of a hyperbola . If there are any two random points each on the x-axis and y-axis on the inverse proportion graph (x) 1 , (x) 2 , (y) 1 , and (y) 2 , such that (x) 1 < (x) 2 and (y) 1 < (y) 2 , the graph will be shown like this:
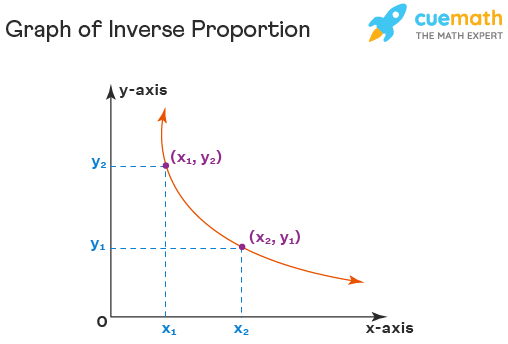
It means if we are increasing the value of x from \(x_{1}\) to \(x_{2}\), the value of y decreases from \(y_{2}\) to \(y_{1}\).
Direct and Inverse Proportion
There are two main types of proportionality - direct proportion and inverse proportion. Two variables x and y are said to be in direct proportion when y ∝ x (or x ∝ y). This implies, y = kx, for a constant k. While two variables x and y are said to be in inverse proportion if y ∝ 1/x (or x ∝ 1/y). This implies y = k/x, for a constant k. In a direct variation relationship, the ratio of two variables is equal for any values, while in inverse proportion the product of two variables is equal for any values. Look at the image given below to understand the distinction between direct and inverse proportion pictorially.
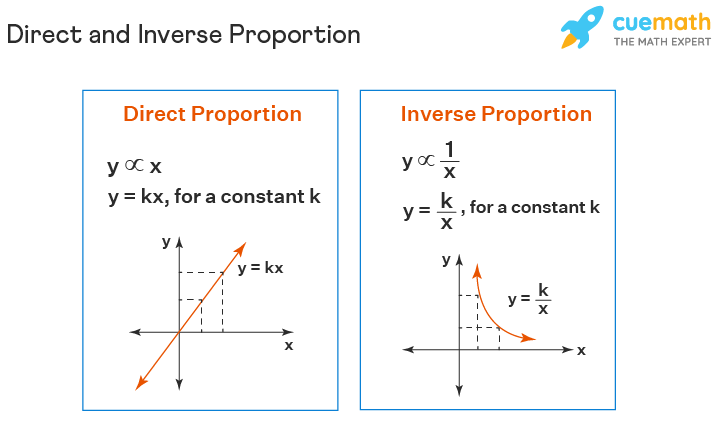
Related Topics
Check these interesting articles related to the concept of inverse proportion.
- Constant of Proportionality
- Direct Proportion
- Percent Proportion
Inverse Proportion Examples
Example 1: Suppose x and y are in an inverse proportion such that when x = 120, y = 5. Find the value of y when x = 150 using the inverse proportion formula.
To find: Value of y. Given: x = 120 when y = 5. x ∝ 1/y x = k / y, where k is a constant, or k = xy Putting, x = 120 and y = 5, we get; k = 120 × 5 = 600 Now, when x = 150, then; 150 y = 600 y = 600/150 = 4 That means when x is increased to 150 then y decreases to 4.
Answer: The value of y is 4 when x = 150.
Example 2: The time taken by a vehicle is 3 hours at a speed of 60 miles/hour. What would be the speed taken to cover the same distance at 4 hours?
Consider speed as m and time parameter as n.
If the time taken increases, then the speed decreases. This is an inverse proportional relation, hence m ∝ 1/n. Using the inverse proportion formula, m = k/ n m × n = k At speed of 60 miles/hour, time = 3 hours, from this we get, k = 60 × 3 = 180 Now, we need to find speed when time, n = 4. m × n = k m × 4 = 180 ∴ m = 180/4 = 45
Therefore, the speed at 4 hours is 45 miles/hour.
Example 3: In a construction company, a supervisor claims that 7 men can complete a task in 42 days. In how many days will 14 men finish the same task?
Consider the number of men be M and the number of days be D. Given: \(M_1\)= 7 , \(D_1\) = 42, and \(M_2\) = 14.
This is an inverse proportional relation, as if the number of workers increases, the number of days decreases.
Considering the first situation, \(M_1\) = k/ \(D_1\)
k = 7 × 42 = 294
Considering the second situation, \(M_2\) = k/ \(D_2\)
14 = 294/ \(D_2\)
\(D_2\) = 294/14 = 21
Answer: It will take 21 days for 14 men to do the same task.
go to slide go to slide go to slide

Book a Free Trial Class
Inverse Proportion Practice Questions
go to slide go to slide
FAQs on Inverse Proportion
What is an indirect proportion.
Indirect or inverse proportion is a relation between two quantities where an increase in one leads to a decrease in the other, and vice-versa. It is just the opposite of direct proportion.
What is the Symbol ∝ Denotes in Inverse Proportion Formula?
In the inverse proportion formula, the proportionate symbol ∝ denotes the relationship between two quantities. It is expressed as x ∝ 1/y. This implies x = k/y, where k is the constant of proportionality.
How do you Find K in Inverse Proportion?
K in inverse proportion represents the constant of proportionality which is the same irrespective of the values of the given variables. To find k in inverse proportion, find the product of x and y. The formula is y = k/x, which gives us k=xy.
How do you Represent the Inverse Proportional Formula?
The inverse proportional formula depicts the relationship between two quantities which can be understood by the formula given below:
- Identify the two quantities which vary in the given problem.
- Identify that there is an inverse variation. x ∝ 1/y
- Apply the Inverse proportion formula x = k/y.
What is the Difference Between Direct and Inverse Proportion?
The difference between direct and inverse proportion is that the direct proportion shows a direct relationship between the two quantities where an increase in one also leads to an increase in the other quantity and vice-versa. On the other hand, inverse proportion represents an indirect relation between two quantities or variables where an increase in one leads to a decrease in the other variable, and vice-versa.
What is the Formula of Inverse Proportion?
The formula of inverse proportion is y = k/x, where x and y are two quantities in inverse proportion and k is the constant of proportionality.
How to Show Relationship Between Two Quantities Using Inverse Proportion Formula?
The inverse proportional relationship between two quantities can be shown if the product of two quantities (x × y) is constant, then they depict an inversely proportional relationship. It is expressed as x ∝ 1/y or x = k/y, where k is the constant of proportionality.
Algebra: Proportion Word Problems
Proportion problems are word problems where the items in the question are proportional to each other. In these lessons, we will learn the two main types of proportional problems: Directly Proportional Problems and Inversely Proportional Problems .
Related Pages: Proportions Direct Variations More Algebra Lessons
The following diagrams show the formulas and graphs for directly proportional and inversely proportional problems. Scroll down the page for examples and solutions.
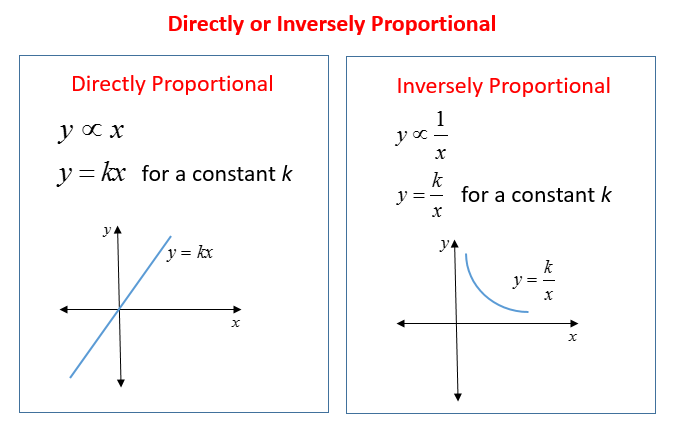
Directly Proportional Problems
There are many situations in our daily lives that involve direct proportion.
For example, a worker may be paid according to the number of hours he worked. The two quantities, the number of hours worked (x) and the amount paid (y), are related in such a way that when x changes, y changes proportionately.
In general, when two variables x and y are such that the ratio \(\frac{y}{x}\) remains a constant, we say that y is directly proportional to x.
If we represent the constant by k, then we can get the equation: \(\frac{y}{x}\) = k or y = kx where k ≠ 0.
In notation, direct proportion is written as y ∝ x
Example 1: If y is directly proportional to x and given y = 9 when x = 5, find: a) the value of y when x = 15 b) the value of x when y = 6
Solution: a) Using the fact that the ratios are constant, we get \(\frac{9}{5}\) = \(\frac{y}{15}\) ⇒ y = \(\frac{9}{5}\) × 15 ⇒ y = 27
b) \(\frac{9}{5}\) = \(\frac{6}{x}\) ⇒ x = \(\frac{5}{9}\) × 6 ⇒ x = \(\frac{10}{3}\) = \(3\frac{1}{3}\)
Example 2: Jane ran 100 meters in 15 seconds. How long did she take to run 2 meter?
Solution: \(\frac{100}{15}\) = \(\frac{y}{2}\) ⇒ y = \(\frac{15}{100}\) × 2 ⇒ y = 0.3
Answer: She took 0.3 seconds.
Example 3: A car travels 125 miles in 3 hours. How far would it travel in 5 hours?
Solution: \(\frac{125}{3}\) = \(\frac{y}{5}\) ⇒ y = \(\frac{125}{3}\) × 5 ⇒ y = \(208\frac{1}{3}\)
Answer: He traveled \(208\frac{1}{3}\) miles.
Basic Proportion Problems
Examples: Use proportions to find the missing value
- 8 inches in 25 minutes ; 28 inches in x minutes
- 3 gallons in 7 hours ; x gallons in 20 hours
Proportion Word Problem
Example: Arthur is typing a paper that is 390 words long. He can type 30 words in a minute. How long will it take for him to type the paper?
Inversely Proportional Problems
There are also many situations in our daily lives that involve inverse proportion.
For example, the number of days required to build a bridge is inversely proportional to the number of workers. As the number of workers increases, the number of days required to build would decrease.
The two quantities, the number of workers (x) and the number of days required (y), are related in such a way that when one quantity increases, the other decreases.
In general, when two variables x and y are such that xy = k where k is a non-zero constant, we say that y is inversely proportional to x.
In notation, inverse proportion is written as y ∝ \(\frac{1}{x}\)
Example: Suppose that y is inversely proportional to x and that y = 8 when x = 3. Calculate the value of y when x = 10.
Solution: Using the fact that the products are constant, we get 3 × 8 = 10y ⇒ y = \(\frac{24}{10}\) = \(2\frac{2}{5}\)
Example: It takes 4 men 6 hours to repair a road. How long will it take 7 men to do the job if they work at the same rate?
Solution: 4 × 6 = 7y ⇒ y = \(\frac{24}{7}\) = \(3\frac{3}{7}\)
Answer: They will take \(3\frac{3}{7}\) hours.
How To Solve A Word Problem That Involves Inverse Proportion
- Suppose x and y are inversely proportional. If x = 24 and y = 18, then what is x when y = 90?
- It will take 30 hours for 8 graders to grade all the USAMTS papers. If the graders all grade at the same rate, then how many graders do we need to get the grading done in 12 hours?
- Ohm’s Law states that current and resistance are inversely proportional. The resistance of a wire is also directly proportional to the length of the wire. If I wish to double the current flowing through a section of a circuit, and all I can change is the length of the wire, then how should I alter the length of the wire?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Math Article
- Direct And Inverse Proportion
Direct and Inverse Proportion

A direct and inverse proportion are used to show how the quantities and amount are related to each other. They are also mentioned as directly proportional or inversely proportional. The symbol used to denote the proportionality is ‘ ∝ ‘. For example, if we say, a is proportional to b, then it is represented as “a ∝ b” and if we say, a is inversely proportional to b, then it is denoted as ‘a∝1/b’. These relations are governed by some proportionality rules. Now in both cases, the value of ‘a’ changes in terms of ‘b’ or when the value of ‘b’ changes, the value of ‘a’ also get changed. The change in both values is equated with a constant of proportionality . Basically, a proportion states that two ratios like a/b and c/d are equal to each other, in such a way, a/b = c/d. In this article, we will learn the definition, examples and also will solve some questions based on the concept.
Direct and Inverse Proportion Definitions
The proportion is said to be a direct proportion between two values when one is a multiple of the other.
For example, 1 cm is equal to 10 mm.
Here, in order to convert cm to mm, the multiplier should be 10.
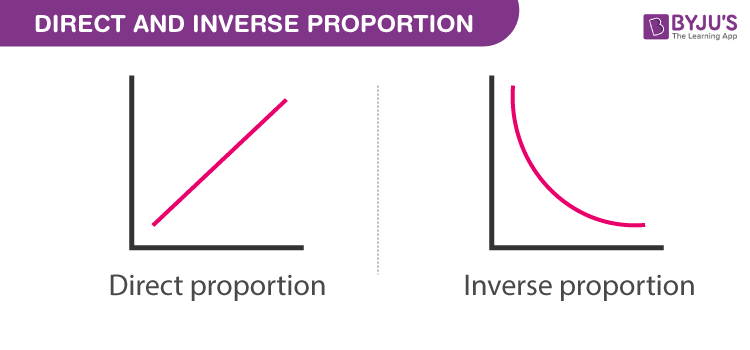
Direct Proportion
Two quantities a and b are said to be in direct proportion if they increase or decrease together. In other words, the ratio of their corresponding values remains constant. This means that,
where k is a positive number, then the quantities a and b are said to vary directly.
In such a case if the values b 1 , b 2 of b corresponding to the values a 1 , a 2 of a, respectively then it becomes;
a 1/ /b 1 = a 2 /b 2
The direct proportion is also known as direct variation .
Directly Proportion Symbol
The symbol used to represent the direct proportion is “ ∝” .
Consider the statement,
a is directly proportional to b
This can be written using the symbol as:
Consider the other statement, a = 2b
In this case, it shows that a is proportional to b, and the value of one variable can be found if the value of other variable is given.
For example:
Therefore, a = 2 x 7 = 14
Similarly, if you take the value of “a” as 14, you will find the value of b
Therefore, b=7
Inverse Proportion
The value is said to inversely proportional when one value increases, and the other decreases. The proportionality symbol is used in a different way. Consider an example; we know that the more workers on a job would reduce the time to complete the task. It is represented as:
Number of workers ∝ (1/ Time taken to complete the job)
Inverse Proportion Definition
Two quantities a and b are said to be in inverse proportion if an increase in quantity a, there will be a decrease in quantity b, and vice-versa. In other words, the product of their corresponding values should remain constant. Sometimes, it is also known as inverse variation
That is, if ab = k, then a and b are said to vary inversely. In this case, if b 1 , b 2 are the values of b corresponding to the values a 1 , a 2 of a, respectively then a 1 b 1 = a 2 b 2 or a 1 /a 2 = b 2 /b 1
The statement ‘a is inversely proportional to b is written as
Here, an equation is given that involves the inverse proportions that can be used to calculate the other values.
Here a is inversely proportional to b
If one value is given, the other value can be easily found.
a= 25/10 = 2.5
Similarly, if a = 2.5, the value of b can be obtained.
b= 25/2.5 = 10
How to Write Direct and Indirect Proportion Equation?
If we have to write a proportionality whether it is direct or indirect in an equation, follow the below steps:
- Step 1: First, write down the proportional symbol
- Step 2: Convert it as an equation using the constant of proportionality
- Step 3: Find the constant of proportionality from the given information
- Step 4: After finding the constant of proportionality, substitute in an equation
Direct and Inverse Proportion Solved Examples
Below are examples to understand the concept of direct and inverse proportion in a better way.
A train is moving at a uniform speed of 75 kilometres/hour.
(i)How many kilometres are covered by train in 20 minutes?
(ii) Find the time required to cover a distance of 250 kilometres.
Let the distance travelled (in km) in 20 minutes be a and time taken (in minutes) to cover 250 km be b.
| Distance travelled (in km) | 75 | a | 250 |
| Time taken (in minutes) | 60 | 20 | b |
We know that 1 hour = 60 minutes
Since the speed of the train is uniform, therefore, the distance covered would be directly proportional to time.
(i) We have 75 /60 = a /20
or (75 /60) 20 = a
So, the train will cover a distance of 25 kilometres in 20 minutes.
(ii) Also, 75/60=250/ b or
b=(250 x 60)/ 75
b = 200 minutes or 3 hours 20 minutes.
Therefore, 3 hours 20 minutes is required to cover a distance of 250 kilometres.
Alternatively, when a is known, then one can determine b, using the relation
a/20 =250/ b
The value f is directly proportional to g. When f = 20, g = 10. Find an equation relating f and g.
Given, f ∝ g
or we can write,
f = kg, where k is the constant proportionality.
20 = k x 10
Therefore, the required equation is;
Practice Questions
- A car is moving at a speed of 60 Km/hr. How far will it travel in 30 minutes?
- If the cost of 10 pens is Rs.120, how much will it cost for 15 pens?
- If 15 workers can do work in 12 days, then how many workers will complete the same work in 6 days?
Frequently Asked Questions on Direct and Inverse Proportion
What is direct and inverse proportion, what is the difference between direct and inverse proportion, what is an example of direct proportion, what is an example of indirect proportion.
For more information and topic-related questions, register with BYJU’S – The Learning App and watch interactive videos to learn with ease.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
we are very glad to have such good apps
wonderful learning app
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

Go Green With Knowledge! Get 30% off on Annual Courses For World Environment Day with code NATURE30

Share this article

Table of Contents
Latest updates.

Ways To Improve Learning Outcomes: Learn Tips & Tricks

Visual Learning Style for Students: Pros and Cons

NCERT Books for Class 6 Social Science 2024 – Download PDF

CBSE Syllabus for Class 9 Social Science 2023-24: Download PDF

CBSE Syllabus for Class 8 Maths 2024: Download PDF

NCERT Books for Class 6 Maths 2025: Download Latest PDF

CBSE Class 10 Study Timetable 2024 – Best Preparation Strategy

CBSE Class 10 Syllabus 2025 – Download PDF

CBSE Syllabus for Class 11 2025: Download PDF

NCERT Solutions for Class 7 Science Chapter 16 Water – A Precious Resource
Tag cloud :.
- entrance exams
- engineering
- ssc cgl 2024
- Written By SHWETHA B.R
- Last Modified 25-01-2023
Inverse Proportion: Definition, Formula, Problems, Examples
Proportion uses to solve various problems in everyday life, such as in business when dealing with transactions or in the kitchen, for example. It establishes a relationship between two or more quantities, making comparison easier. When the value of one item rises concerning a decrease in another or vice versa, two quantities are said to be inversely proportional. This means that in nature, these two quantities are opposed. For example, the time it takes to perform a task lowers as the number of workers completing it increases, and it increases as the number of workers drops. In this article, we will be covering Inverse Proportion in detail.
Proportionality
We study quantities that depend on one another in mathematics and physics, and these values are referred to as proportional to one another. In other words, two variables or quantities are proportional to one another, meaning that if one is changed, the other also changes by the same amount. Proportionality is the word for this feature of variables, and the sign for proportionality is proportionality is “\( \propto \)”.
There are two categories of proportionality of variables. They are:
Directly Proportional
- Inversely Proportional

Variables or quantities that are directly proportional are those in which as one increases, the other increases as well. They are directly proportional when an increase in one quantity causes an increase in the other and vice versa.
Example: If the number of individuals visiting a resort increases, earning of the resort also increases and vice versa.
Direct Proportion Formula
According to the direction proportion formula, if amount \(y\) is directly proportional to quantity \(x\), we can say:
\(\frac{x}{y}=k\)
The formula for direct proportion is \(x=k y\), where \(k\) is proportionality constant.
Here, as \(x\) grows, \(y\) grows as well. And, as \(x\) drops, \(y\) decreases as well.
Inverse Proportion

Two quantities are inversely proportional when an increase in one causes a decrease in the other and vice versa.
Consider the relationship between speed and time. Speed and travel time are inversely linked because the faster we travel, the less time we spend travelling, i.e., the faster we travel, the less time we spend travelling.
Inverse Proportion Examples

- If we increase the bike’s speed, then the time taken to reach the destination decreases.
- The brightness of the sunlight decreases as the distance from the sun increases.
- More vehicles on the road mean there is less space on the road.
- The lesser the number of workers, the more time it takes to finish the work and vice versa.
- The number of people and the share each gets from a fixed quantity of something in inverse proportion.
Inverse Proportion Formula
The proportional relationship between two quantities is denoted by the symbol “\(\propto \)”. Let \(x\) and \(y\) be two different numbers. If \(y\) is inversely proportional to \(x\), it is the same as if \(y\) is directly proportional to \(\frac{1}{x}\). Then \(y\) is said to be inversely proportional to \(x\) and is expressed as \(y \propto \frac{1}{x}\) in mathematics.
Hence, we shall write, \(y=\frac{k}{x}\) where \(k\) is the proportionality constant, is the general equation for inverse proportion.
Two quantities \(x\) and \(y\) are said to vary inversely if there exists a relation of the type \(x y=k\) between them, where \(k\) is a positive constant number.
If \(x_{1}\) and \(x_{2}\) are two values of \(x\), and \(y_{1}\) and \(y_{2}\) are the corresponding values of \(y\). Then, \(x_{1} \times y_{1}=x_{2} \times y_{2}=\,\text {constant}\)
Therefore, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\)
An increase in one quantity leads to a decrease in the other quantity in the inverse proportion.
This result is important as it helps us to solve inverse variation problems.
Inverse Proportion Graph
When two quantities have an inverse relationship, when one rises, the other falls, we get a curved graph when we graph this relationship.
If \(y\) is inversely proportional to \(x\), it is the same as if \(y\) is directly proportional to \(\frac{1}{x}\). Then \(y\) is said to be inversely proportional to \(x\) and is expressed as \(y = k \times \frac{1}{x}.\)

Difference Between Direct and Inverse Proportional Graph

Applications of Inverse Proportion
Inversely proportionality is a term that is commonly utilized in everyday life. Inverse proportion helps to solve numerous problems in science, statistics, and other fields. In physics, the concept of inverse proportionality is used to create several formulas. Ohm’s law, the speed and time relationship, the wavelength and frequency of sound are only a few examples.

Solved Examples – Inverse Proportion
Q.1. A brick wall is being cemented by 12 men. The work is completed in 18 days. If 18 men do the same work, how long will it take to complete the work? Ans: Let the number of days to complete the work \(18\) days be \(y\). The more men, the less will be the time taken. Therefore, the two quantities vary inversely.
| Number of men \((x)\) | \(12\) | \(18\) |
| Number of days \((y)\) | \(18\) | \(y\) |
So, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\) \(\Longrightarrow \frac{12}{18}=\frac{y}{18}\) \(\Rightarrow y=\frac{18 \times 12}{18}\) \(\Rightarrow x=12\) Therefore, the time taken is \(12\) days.
Q.2. If 40 workers can finish a job in 15 days, how many workers should be employed if the job is to be finished in 8 days. Ans: Let the number of workers to be employed to finish the job in \(8\) days be \(x\). The more the number of workers, the less will be the time taken. Therefore, the two quantities vary inversely.
| Number of workers \((x)\) | \(40\) | \(x\) |
| Number of days \((y)\) | \(15\) | \(8\) |
So, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\) \( \Rightarrow \frac{x}{{40}} = \frac{{15}}{8}\) \( \Rightarrow x = \frac{{40 \times 15}}{8}\) \(\Rightarrow x=75\) Therefore, \(75\) workers are required.
Q.3. 20 women can do a job in 5 days. In how many days can 25 women do the same job? Ans: Let the number of days to complete the job is \(y\). The more the number of workers, the less will be the time taken. Therefore, the two quantities vary inversely.
| Number of women \((x)\) | \(20\) | \(25\) |
| Number of days \((y)\) | \(5\) | \(y\) |
So, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\) \(\Longrightarrow \frac{20}{25}=\frac{y}{5}\) \(\Rightarrow y=\frac{20 \times 5}{25}\) \(\Rightarrow x=4\) Therefore, in \(4\) days, \(25\) women do the same job.
Q.4. 12 men can dig a pond in 8 days. How many men can dig it in 6 days? Ans: Let the number of men dig a pond is \(x\). The more the number of workers, the less will be the time taken. Therefore, the two quantities vary inversely.
| Number of men \((x)\) | \(12\) | \(x\) |
| Number of days \((y)\) | \(8\) | \(6\) |
So, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\) \( \Rightarrow \frac{{12}}{x} = \frac{6}{8}\) \(\Rightarrow x=\frac{12 \times 8}{6}\) \(\Rightarrow x=16\) Therefore, in \(16\) men can dig the same job in \(6\) days.
Q.5. 20 kg rice lasts 30 days in a family of 8 people. If 2 guests stay with the family. How many days will 20 kg of rice last? Ans: Let the time the rice lasts when the number of people is \(8+2=10\), be \(y\).
| Number of people \((x)\) | \(8\) | \(10\) |
| Time the rice lasts \((y)\) | \(30\) | \(y\) |
The more the people, the less the time the rice will last. Hence, the number of people and time the rice will last vary inversely. We therefore have, So, \(\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}\) \(\Rightarrow \frac{8}{10}=\frac{y}{30}\) \(\Rightarrow y=\frac{30 \times 8}{10}\) \(\Longrightarrow y=24\) Therefore, the rice will last in \(24\) days.

When two quantities are inversely proportional, that is, when an increase in one causes a decrease in the other and vice versa, they are called inversely proportional. When one variable decline in inverse proportion, the further increases in the same proportion. This article includes the definition of proportion, direct and indirect proportion, formulas, and graphs.
It helps for a better understanding of the inverse proportion. The outcome of this inverse proportion topic helps in solving different problems based on it.
Frequently Asked Questions (FAQs) – Inverse Proportion
Q.1. What is the formula of inverse proportion? Ans: The proportional relationship between two quantities is denoted by the symbol “\(\propto\)”. Let \(x\) and \(y\) be two different numbers. If \(y\) is inversely proportional to \(x\), it is the same as if \(y\) is directly proportional to \(\frac{1}{x}\). Then \(y\) is said to be inversely proportional to \(x\) and is expressed as \(y \propto \frac{1}{x}\) in mathematics. \(y=\frac{k}{x}, w\) here \(k\) is the proportionality constant, is the general equation for inverse variation.
Q.2. What is an inverse proportion? Ans: When two quantities are inversely proportional, that is, when an increase in one causes a decrease in the other and vice versa, they are called inversely proportional. When one variable decline in inverse proportion, the further increases in the same proportion.
Q.3. What is the formula of direct and inverse proportion? Ans: \(x \propto y\) is written when two quantities \(x\) and \(y\), are directly proportional (or vary directly). The symbol “\(\propto\)” means “is proportionate to”. \(y \propto \frac{1}{x}\) is written when two quantities \(x\) and \(y\) are in inverse proportion (or vary inversely).
Q.4. What is the difference between direct and inverse proportion? Ans: If we split two matching amounts in a direct proportion, the ratio between them remains the same. On the other hand, in an inverse or indirect proportion, as one item increases, the other automatically declines.
Q.5. What is k in inverse proportion? Ans: If \(y\) is inversely proportional to \(x\), it is the same as if \(y\) is directly proportional to \(\frac{1}{x}\). Then \(y\) is said to be inversely proportional to \(x\) and is expressed as \(y \propto \frac{1}{x}\) in mathematics. Hence, \(y=\frac{k}{x}\), where \(k\) is the proportionality constant, is the general equation for inverse variation.
We hope this detailed article on the concept of inverse proportion helped you in your studies. If you have any doubts, queries or suggestions regarding this article, feel to ask us in the comment section and we will be more than happy to assist you. Happy learning!
Related Articles
Ways To Improve Learning Outcomes: With the development of technology, students may now rely on strategies to enhance learning outcomes. No matter how knowledgeable a...
Visual Learning Style: We as humans possess the power to remember those which we have caught visually in our memory and that too for a...
NCERT Books for Class 6 Social Science 2024: Many state education boards, including the CBSE, prescribe the NCRET curriculum for classes 1 to 12. Thus,...
CBSE Syllabus for Class 9 Social Science: The Central Board of Secondary Education releases the revised CBSE Class 9 Social Science syllabus. The syllabus is...
CBSE Syllabus for Class 8 Maths 2023-24: Students in CBSE Class 8 need to be thorough with their syllabus so that they can prepare for the...
NCERT Books for Class 6 Maths 2025: The National Council of Educational Research and Training (NCERT) textbooks are the prescribed set of books for schools...
CBSE Class 10 Study Timetable: The CBSE Class 10 is the board-level exam, and the Class 10th students will appear for the board examinations for...
CBSE Class 10 Syllabus 2025: The Central Board of Secondary Education (CBSE) conducts the Class 10 exams every year. Students in the CBSE 10th Class...
CBSE Syllabus for Class 11 2025: The Central Board of Secondary Education (CBSE) has published the Class 11 syllabus for all streams on its official...
NCERT Solutions for Class 7 Science Chapter 16 Water – A Precious Resource: In this chapter, students will study about the importance of water. There are three...
NCERT Solutions for Class 7 Science Chapter 10 2024: Respiration in Organisms
NCERT Solutions for Class 7 Science Chapter 10 Respiration in Organisms: NCERT solutions are great study resources that help students solve all the questions associated...
Factors Affecting Respiration: Definition, Diagrams with Examples
In plants, respiration can be regarded as the reversal of the photosynthetic process. Like photosynthesis, respiration involves gas exchange with the environment. Unlike photosynthesis, respiration...
NCERT Solutions for Class 7 Science Chapter 12
NCERT Solutions for Class 7 Science Chapter 12 Reproduction in Plants: The chapter 'Reproduction' in Class 7 Science discusses the different modes of reproduction in...
NCERT Solutions for Class 7 Science Chapter 11
NCERT Solutions for Class 7 Science Chapter 11: Chapter 11 of Class 7 Science deals with Transportation in Animals and Plants. Students need to ensure...
NCERT Solutions for Class 7 Science Chapter 15: Light
NCERT Solutions for Class 7 Science Chapter 15: The NCERT Class 7 Science Chapter 15 is Light. It is one of the most basic concepts. Students...
NCERT Solutions for Class 7 Science Chapter 13
NCERT Solutions for Class 7 Science Chapter 13: Chapter 13 in class 7 Science is Motion and Time. The chapter concepts have a profound impact...
NCERT Solutions for Class 7 Science Chapter 14: Electric Current and its Effects
NCERT Solutions for Class 7 Science Chapter 14: One of the most important chapters in CBSE Class 7 is Electric Current and its Effects. Using...
General Terms Related to Spherical Mirrors
General terms related to spherical mirrors: A mirror with the shape of a portion cut out of a spherical surface or substance is known as a...
Animal Cell: Definition, Diagram, Types of Animal Cells
Animal Cell: An animal cell is a eukaryotic cell with membrane-bound cell organelles without a cell wall. We all know that the cell is the fundamental...
NCERT Solutions for Class 10 Science 2024 – Download PDF
NCERT Solutions for Class 10 Science: The National Council of Educational Research and Training (NCERT) publishes NCERT Solutions for Class 10 Science as a comprehensive...
NCERT Books for Class 12 Chemistry 2024: Download PDF
NCERT Books for class 12 Chemistry: NCERT publishes chemistry class 12 books every year. The NCERT chemistry class 12 books are essential study material for...
CBSE Class 9 Mock Tests 2025: Attempt Online Mock Test Series (Subject-wise)
We all have heard at least once that the secret to success is practice. Some of you could say it's a cliché, but those who...
NCERT Books for Class 10 Maths 2025: Download Latest PDF
NCERT Books for Class 10 Maths: The NCERT Class 10 Maths Book is a comprehensive study resource for students preparing for their Class 10 board exams....
Arc of a Circle: Definition, Properties, and Examples
Arc of a circle: A circle is the set of all points in the plane that are a fixed distance called the radius from a fixed point...
CBSE Class 10 Mock Test 2025: Practice Latest Test Series
CBSE Class 10 Mock Test 2025: Students' stress is real due to the mounting pressure of scoring good marks and getting into a renowned college....
NCERT Solutions for Class 10 2024: Science and Maths
NCERT Solutions for Class 10 2024: Students appearing for the CBSE Class 10 board exam must go through NCERT Solutions to prepare for the exams...
NCERT Solutions for Class 12 2024 – Physics, Chemistry, Maths, Biology
NCERT Solutions for Class 12 2023-24: The NCERT Solutions for Class 12 are meant to help students understand what the subject holds. These solutions are...

39 Insightful Publications

Embibe Is A Global Innovator

Innovator Of The Year Education Forever

Interpretable And Explainable AI

Revolutionizing Education Forever

Best AI Platform For Education

Enabling Teachers Everywhere

Decoding Performance

Leading AI Powered Learning Solution Provider

Auto Generation Of Tests

Disrupting Education In India

Problem Sequencing Using DKT

Help Students Ace India's Toughest Exams

Best Education AI Platform

Unlocking AI Through Saas

Fixing Student’s Behaviour With Data Analytics

Leveraging Intelligence To Deliver Results

Brave New World Of Applied AI

You Can Score Higher

Harnessing AI In Education

Personalized Ed-tech With AI

Exciting AI Platform, Personalizing Education

Disruptor Award For Maximum Business Impact

Top 20 AI Influencers In India

Proud Owner Of 9 Patents

Innovation in AR/VR/MR

Best Animated Frames Award 2024
Trending Searches
Previous year question papers, sample papers.
Practice Inverse Proportion Questions with Hints & Solutions

Practice Inverse Proportion Questions with Solutions & Ace Exam
Enter mobile number.
By signing up, you agree to our Privacy Policy and Terms & Conditions
WORD PROBLEMS ON INVERSE PROPORTION
Inverse proportion :
Inverse proportion is a situation where an increases in one quantity causes a corresponding decreases in the other quantity.
Inverse proportion is a situation where an decreases in one quantity causes a corresponding increases in the other quantity.
Problem 1 :
6 pumps are required to fill a water sump in 1 hr 30 minutes. What will be the time taken to fill the sump if one pump is switched off ?
Let x be the required time taken.
As the number of pumps increases the time taken to fill the sump will be less.
It comes under inverse proportion.
90 ⋅ 6 = x ⋅ 5
540 = x ⋅ 5
540/5 = x
108/60 = 1 hour 48 min
Therefore, the time taken to fill the sump is 1 hour 48 min.
Problem 2 :
A farmer has enough food for 144 ducks for 28 days. If he sells 32 ducks, how long will the food last?
Let the required number of days be x.
As the number of ducks decreases the food will last for more days.
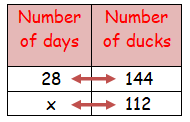
28 ⋅ 144 = x ⋅ 112
4032 = x ⋅ 112
4032/112 = x
36 = x
Therefore, the food last for 36 days.
Problem 3 :
If takes 60 days for 10 machines to dig a hole. Assuming that all machines work at the same speed, how long will it take 30 machines to dig the same hole?
Let the number of days required be x.
As the number of machines increases it takes less days to complete the work.
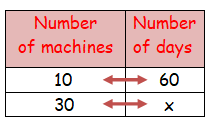
10 ⋅ 60 = 30 ⋅ x
600 = 30 ⋅ x
Therefore, it takes 20 days to dig the hole.
Problem 4 :
Forty students stay in a hostel. They had food stock for 30 days. If the students are doubled then for how many days the stock will last?
Let x be the required number of days.
As the number of students increases the food last for less number of days.
30 ⋅ 40 = x ⋅ 80
1200 = x ⋅ 80
1200/80 = x
Therefore, the food stock lasts for 15 days.
Problem 5 :
Meena had enough money to send 8 parcels each weighing 500 grams through a courier service. What would be the weight of each parcel, if she has to send 40 parcels for the same money?
Let the weight of parcel be x grams.
As the number of parcels increases weight of a parcel decreases.
8 ⋅ 500 = 40 ⋅ x
4000 = 40 ⋅ x
4000/40 = x
Therefore, the weight of each parcel is 100 grams.
Problem 6 :
If takes 120 minutes to weed a garden with 6 gardeners if the same work is to be done in 30 minutes, how many more gardeners are needed?
Let the number of gardeners needed be x.
As the number of gardeners increases the time decreases.

6 ⋅ 120 = x ⋅ 30
720 = x ⋅ 30
To complete the work in 30 min gardeners needed = 24.
Already existing gardeners = 6
Therefore, 18 more gardeners are needed.
Problem 7 :
Heena goes by bi-cycle to her school every day. Her average speed is 12 km/hr. and she reaches school in 20 minutes. What is the increase in speed, if she reaches the school in 15 minutes?
Let the speed to reach school in 15 minutes be x.
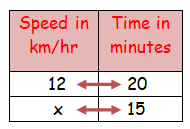
If she reaches the school in 15 minutes the speed = 16 km/hr.
Already running with 12 km/hr.
Increased speed = 16 – 12 = 4 km/hr.
Therefore, the increase in speed is 4 km/hr.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Digital sat math problems and solutions (part - 30).
Aug 19, 24 08:09 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Aug 19, 24 08:07 AM
Solving Exponential Equations Problems and Solutions (Part -2)
Aug 18, 24 11:16 PM
R10b – Solving problems involving inverse proportion
This is the students’ version of the page. Log in above for the teachers’ version.
- A knowledge of the four operations from lessons N2a , N2b , N2c , N2d , N2e and N2f is assumed.
- N3b – Order of operations, including brackets, powers, roots and reciprocals
- R10a – Solving problems involving direct proportion including graphical and algebraic representations
- A12a – Graphs of linear functions, quadratic functions, simple cubic functions, and the reciprocal function
- A14a – Plotting and interpreting graphs (including reciprocal graphs and exponential graphs) and graphs of non-standard functions
An illustration of quantities in inverse proportion
Solving problems involving inverse proportion.


IMAGES
COMMENTS
Example 1: complete the table y ∝ ⅟ x. Given that y y is inversely proportional to x, x, calculate the missing value of y y in the table below. Write down the inverse proportion formula. As y\propto\frac {1} {x}, y ∝ x1, we can write the formula y=\frac {k} {x}. y = xk. 2 Determine the value of \textbf {k} k.
Click here for Answers. variation, proportionality. Practice Questions. Previous: Pythagoras Practice Questions. Next: Probability Practice Questions. The Corbettmaths Practice Questions on Direct and Inverse Proportion.
If the variable a is inversely proportional to the variable b, then this can be represented with the formula: a \propto \frac {1} {b} a ∝ b1. If we change the sign of proportionality to the equal sign, we have the equation: ab=k ab = k. where k is the constant of proportionality. To find an inverse proportion equation, we have to start by ...
Corbettmaths - This video explains how to solve inverse proportion questions.
This video shows how to solve inverse proportion questions. It goes through a couple of examples and ends with some practice questions. Example 1: A is inversely proportional to B. When A is 10, B is 2. Find the value of A when B is 8. Example 2: F is inversely proportional to the square of x. When A is 20, B is 3. Find the value of F when x is 5.
More examples on Inverse Variation word problems: 3. 6 oxen or 8 cows can graze a field in 28 days. How long would 9 oxen and 2 cows take to graze the same field? Solution: 6 oxen = 8 cows. ⇒ 1 ox = 8/6 cows. ⇒ 9 oxen ≡ (8/6 × 9) cows = 12 cows. ⇒ (9 oxen + 2 cows) ≡ (12 cows + 2 cows) = 14 cows. Now, 8 cows can graze the field in 28 ...
Here's a worksheet & walkthrough video on proportion: https://youtu.be/LCsUJ9N2pck. Hope it helps! S :-) How to work with inverse proportionThis video deals ...
Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers. Worksheet Name. 1. 2. 3. Direct Proportionality - Basics. 1. 2.
A video revising the techniques and strategies for solving inverse proportion problems. (Higher & Foundation).This video is part of the Ratio & Proportion mo...
Inverse Proportion. Inverse proportion is when two quantities change opposite to one another. As one quantity increases, the other quantity decreases. When the two quantities are multiplied, the same constant occurs. A common example of inverse proportion is to calculate the time it takes to do a job with more or fewer workers.
Solving direct and inverse proportion questions will help you to solve many real-world problems. Also, practise additional questions on direct proportion and inverse proportion here in this article. Direct and Inverse Proportion - Meaning. Suppose two variables or quantities change in the same direction, they are said to be in direct proportion.
Inverse Proportionality - The Basics. If two quantities are inversely proportional, then as one increases the other decreases at the same rate (proportionally), e.g. as one doubles, the other one halves. Example: \textcolor{blue}{6} builders can build \textcolor{red}{10} houses in 30 months. How long would it take \textcolor{purple}{18} builders to build the same number of houses?
Speed and travel time are Inversely Proportional because the faster we go the shorter the time. As speed goes up, travel time goes down. And as speed goes down, travel time goes up. This: y is inversely proportional to x. Is the same thing as: y is directly proportional to 1/x. Which can be written: y = k x.
Inverse Proportion Video . inversely. Videos
The relationship between speed and time, denoted as y and x, can be expressed mathematically as the inverse proportion formula. Written as follows is the inverse proportional formula: y=$\frac {k} {x}$. Take note of the following: k is the constant of proportionality. As x decreases, y increases.
Inverse Proportion Examples. Example 1: Suppose x and y are in an inverse proportion such that when x = 120, y = 5. Find the value of y when x = 150 using the inverse proportion formula. Solution: To find: Value of y. Given: x = 120 when y = 5. x ∝ 1/y. x = k / y, where k is a constant, or k = xy.
A video revising the techniques and strategies for solving direct and inverse proportion problems. (Higher Only).This video is part of the Ratio & Proportion...
In notation, direct proportion is written as. y ∝ x. Example 1: If y is directly proportional to x and given y = 9 when x = 5, find: a) the value of y when x = 15. b) the value of x when y = 6. Solution: a) Using the fact that the ratios are constant, we get. 95 9 5 = y 15 y 15.
Direct and Inverse Proportion. A direct and inverse proportion are used to show how the quantities and amount are related to each other. They are also mentioned as directly proportional or inversely proportional. The symbol used to denote the proportionality is ' ∝ '. For example, if we say, a is proportional to b, then it is represented ...
Inversely proportionality is a term that is commonly utilized in everyday life. Inverse proportion helps to solve numerous problems in science, statistics, and other fields. In physics, the concept of inverse proportionality is used to create several formulas. Ohm's law, the speed and time relationship, the wavelength and frequency of sound ...
As the number of machines increases it takes less days to complete the work. It comes under inverse proportion. 10 ⋅ 60 = 30 ⋅ x. 600 = 30 ⋅ x. 600/30 = x. 20 = x. Therefore, it takes 20 days to dig the hole. Problem 4 : Forty students stay in a hostel.
Prerequisites. N3b - Order of operations, including brackets, powers, roots and reciprocals. R10a - Solving problems involving direct proportion including graphical and algebraic representations. A12a - Graphs of linear functions, quadratic functions, simple cubic functions, and the reciprocal function. A14a - Plotting and interpreting ...