how to analyze problem solving in math

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Problem Analysis in Math: Using the 5-Step Problem-Solving Approach

This blog will explore the ways in which problem analysis of student mathematics difficulties can be applied within a problem-solving approach. We will review the core principles of a multi-tier system of support (MTSS) framework, identify the steps within a problem-solving approach, and explore the ways in which problem analysis helps to inform intervention development within the context of mathematics instruction.

Core Principles of an MTSS Framework

A variety of definitions of an MTSS framework exist within the field of education; however, several common principles are apparent and have helped to shape much of the work within this area. The National Association of State Directors of Special Education (Batsche et al., 2006) define eight core principles that capture some of the most important aspects and core beliefs of an MTSS framework:

• We can effectively teach all children.
• Intervene early.
• Use a multi-tier model of service delivery.
• Use a problem-solving model to make decisions within a multi-tier model.
• Use scientific, research-based validated intervention and instruction to the extent available.
• Monitor student progress to inform instruction.
• Use data to make decisions.
• Use assessment for screening, diagnostics, and progress monitoring.

The fourth core principle refers to utilizing a problem-solving model to make decisions. More specifically, educators and administrators should use a clearly defined problem-solving process that guides their team in identifying the problem, analyzing the size and effect of the problem, developing a plan for intervention to address the problem, implementing the plan, and examining the effectiveness of the intervention plan.

5-Step Problem-Solving Approach

The problem-solving approach utilized by the FastBridge Learning ® system includes the following five steps:

Problem identification

• Problem analysis
• Plan development
• Plan implementation
• Plan evaluation

Following this 5-step problem-solving approach helps to guide school teams of educators and administrators in engaging in data-based decision making: a core principle of the MTSS framework.

The first step in this problem-solving approach is problem identification. Christ and Arañas (2014) define a problem as a discrepancy between observed and expected performance. Regularly scheduled universal screening plays an important role in problem identification. The FastBridge Learning ® system offers a variety of screening measures for mathematics, which are summarized in the table below. While the results of regularly scheduled universal screening help to inform whether or not a discrepancy between observed and expected performance exists, problem analysis aims to identify the size and effects of the problem.

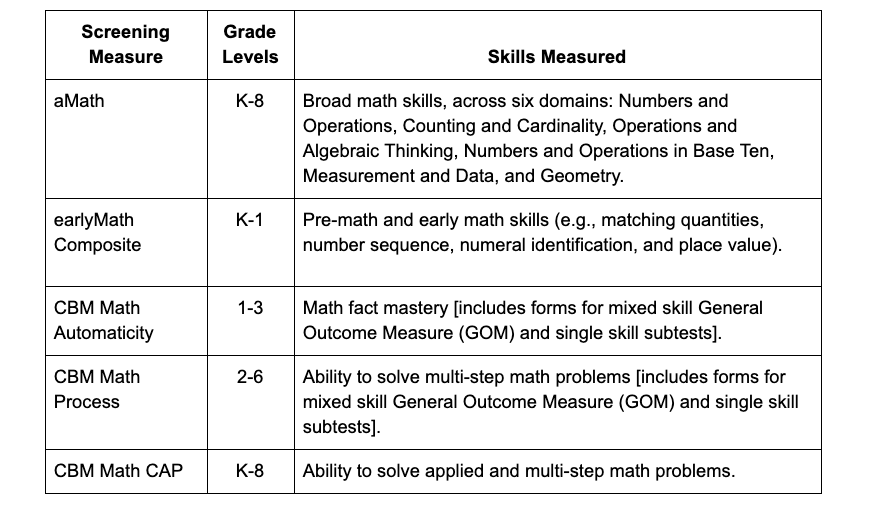
Problem Analysis

After a problem has been identified, the problem must be defined through the method of problem analysis. Only after a problem has been sufficiently analyzed and defined, can the significance of a problem be understood (Brown-Chidsey & Bickford, 2016). Problem analysis can occur at both the individual level and the group level.

Problem Analysis at the Individual Leve l

At the individual level, a discrepancy between observed and expected performance may appear within an individual’s universal screening results. FastBridge Learning ® Individual Skills Reports can provide detailed information to support problem analysis. The Individual Skills Report provides a snapshot of a given student’s risk, relative to benchmark goals, and also provides detailed results on an item-by-item basis. This item-by-item analysis provides insight into the skills the student demonstrates and which skills may require additional instructional support.

If the student’s performance is relatively close to the benchmark goal, the problem is likely to be understood as a minor problem. Item-by-item analysis can help a teacher determine if targeted reteaching of specific content may help the student to reach the goal, or if more intensive intervention may be necessary. An example of a FastBridge Learning ® Individual Skills Report for the earlyMath subtest Numeral Identification (Kindergarten) may be seen below.

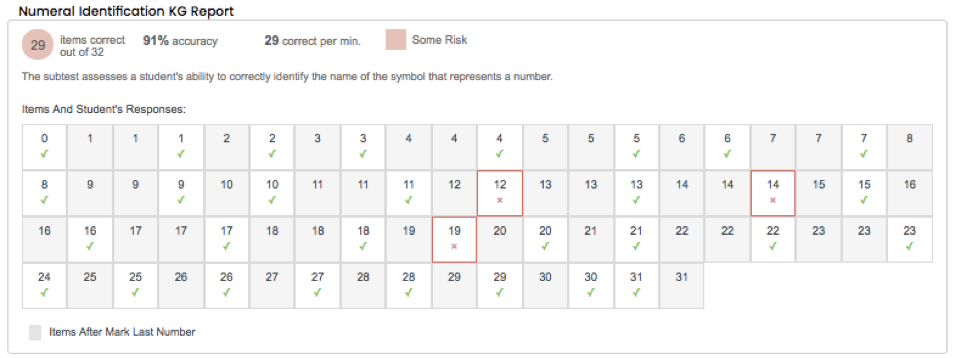
The above report suggests that the sample student is at “some risk” for difficulty with numeral identification. It also reveals that the student was able to identify the given numerals with 91% accuracy. Additionally, the item-by-item analysis indicates that the student struggled to identify the following numerals: 12, 14, and 19. In this case, problem analysis may suggest that this is a minor problem, which may be remedied through targeted reteaching of the numerals 12, 14, and 19. In contrast, if during problem analysis, an Individual Skills Report for Numeral Identification indicated very low accuracy and a substantial number of misidentified numerals, the results would suggest a more significant problem. Significant problems warrant planning for more intensive intervention.

Problem analysis at the group level

At the group level, problem analysis seeks to determine the size and effects of a problem at the class, grade, or school-wide level. FastBridge Learning ® Group Screening Reports and Group Skills Reports help to provide insight about groups of students at risk for learning difficulties. An example of a Group Screening Report for earlyMath may be seen below.

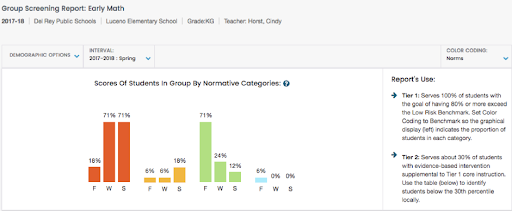
The Group Screening Report pictured above indicates that approximately 77% of Ms. Horst’s kindergarten class scored at or above the benchmark goal on the earlyMath Composite during the fall benchmark period, while 6% and 18% were identified as being at “some risk” and “high risk” respectively.

All students should demonstrate growth in math achievement throughout the school year. If there are students who met the fall benchmark for mathematics, but not the winter and/or spring benchmarks, problem analysis must occur. In Ms. Horst’s class, we can see by the spring benchmark period, only 12% of her kindergarten class scored at or above the benchmark goal on the earlyMath composite, while 18% and 71% were identified as being at “some risk” and “high risk” respectively.

Problem analysis at the group level may aim to answer questions such as the following:

• What type of mathematics instruction was provided for these students?
• Did other kindergarten classrooms within the school experience a similar pattern of mathematics difficulty?
• With which specific mathematics skills (e.g., decomposing, number sequencing, numeral identification) did the group demonstrate success and difficulty?
• How close to the end-of-year mathematics goals are the students now?

In order to complete a thorough problem analysis, supplemental data about student performance and instructional practices may need to be collected.

For instance, classroom observations and/or a teacher interview would provide insight into the first question. Group Screening Reports for the other kindergarten classrooms in the school could help identify if this is a schoolwide pattern of difficulty or a classroom-specific pattern of difficulty. An analysis of the Group Skills Report for Ms. Horst’s class would provide insight into students’ strengths and weaknesses across the earlyMath Composite’s subtests. Additional, targeted, follow-up assessment using selected FastBridge Learning ® earlyMath subtests could help to gather information about the final question.

The goal of problem analysis is to determine the significance of a problem and to develop a hypothesis about why a problem has occurred. The information gathered during the problem analysis stage is then used to inform the third step of the 5-step problem-solving approach: plan development.

Batsche, G., Elliott, J., Graden, J. L., Grimes, J., Kovaleski, J. F., Prasse, D., Schrag, J., & Tilly, W.D. (2006). Response to intervention: Policy considerations and implementation. Alexandria, VA: National Association of State Directors of Special Education, Inc.

Brown-Chidsey, R. and Bickford, R. (2016). Practical handbook of multi-tiered systems of support: Building academic and behavioral success in schools. New York, NY: The Guilford Press.

Christ, T.J., & Arañas, Y.A. (2014). Best practices in problem analysis. In A. Thomas & J. Grimes (Eds.), Best Practices in School Psychology VI . Bethesda, MD: National Association of School Psychologists.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

What are your chances of acceptance?

Calculate for all schools, your chance of acceptance.

Your chancing factors

Extracurriculars.

Guide to SAT Math Problem Solving and Data Analysis + Practice Questions

Do you know how to improve your profile for college applications.

See how your profile ranks among thousands of other students using CollegeVine. Calculate your chances at your dream schools and learn what areas you need to improve right now — it only takes 3 minutes and it's 100% free.

Show me what areas I need to improve

What’s Covered:

Overview of sat math problem solving and data analysis, how will the sat impact my college chances.

• Strategies for Problem Solving and Data Analysis Questions
• Practice Questions for Problem Solving and Data Analysis

Final Tips and Strategies

Problem Solving and Data Analysis questions appear on the Calculator section of the SAT Math test and involve applying mathematical knowledge to real-world contexts. These problems can be tough, so if you want to improve your math score, here are some strategies and practice problems to help you out.

The SAT Math section contributes to half of the total SAT score. This section is scored out of 800 and includes three main categories, which each have a subscore out of 15.

Here is the breakdown of each category:

• Heart of Algebra: 33%
• Problem Solving and Data Analysis: 29%
• Passport to Advanced Math: 28%

Additional Topics in Math covers the remaining 10% and consists of a variety of different mathematical topics.

The Problem Solving and Data Analysis section tests students’ ability to solve real-world problems using mathematical understanding and skills. This includes quantitative reasoning, interpreting and synthesizing data, and creating representations. These questions never appear on the SAT No Calculator section, so you’ll always be allowed a calculator for them.

Problem Solving and Data Analysis questions ask students to:

• Use ratios, rates, proportional relationships, and scale drawings to solve single- and multistep problems.
• Solve single- and multi-step problems involving percentages.
• Solve single- and multi-step problems involving measurement quantities, units, and unit conversion. 
• Given a scatterplot, use linear, quadratic, or exponential models to describe how the variables are related.
• Use the relationship between two variables to investigate key features of the graph.
• Compare linear growth with exponential growth. 
• Use two-way tables to summarize categorical data and relative frequencies, and calculate conditional probability. 
• Make inferences about population parameters based on sample data. 
• Use statistics to investigate measures of center of data and analyze shape, center, and spread. 
• Evaluate reports to make inferences, justify conclusions, and determine appropriateness of data collection methods.

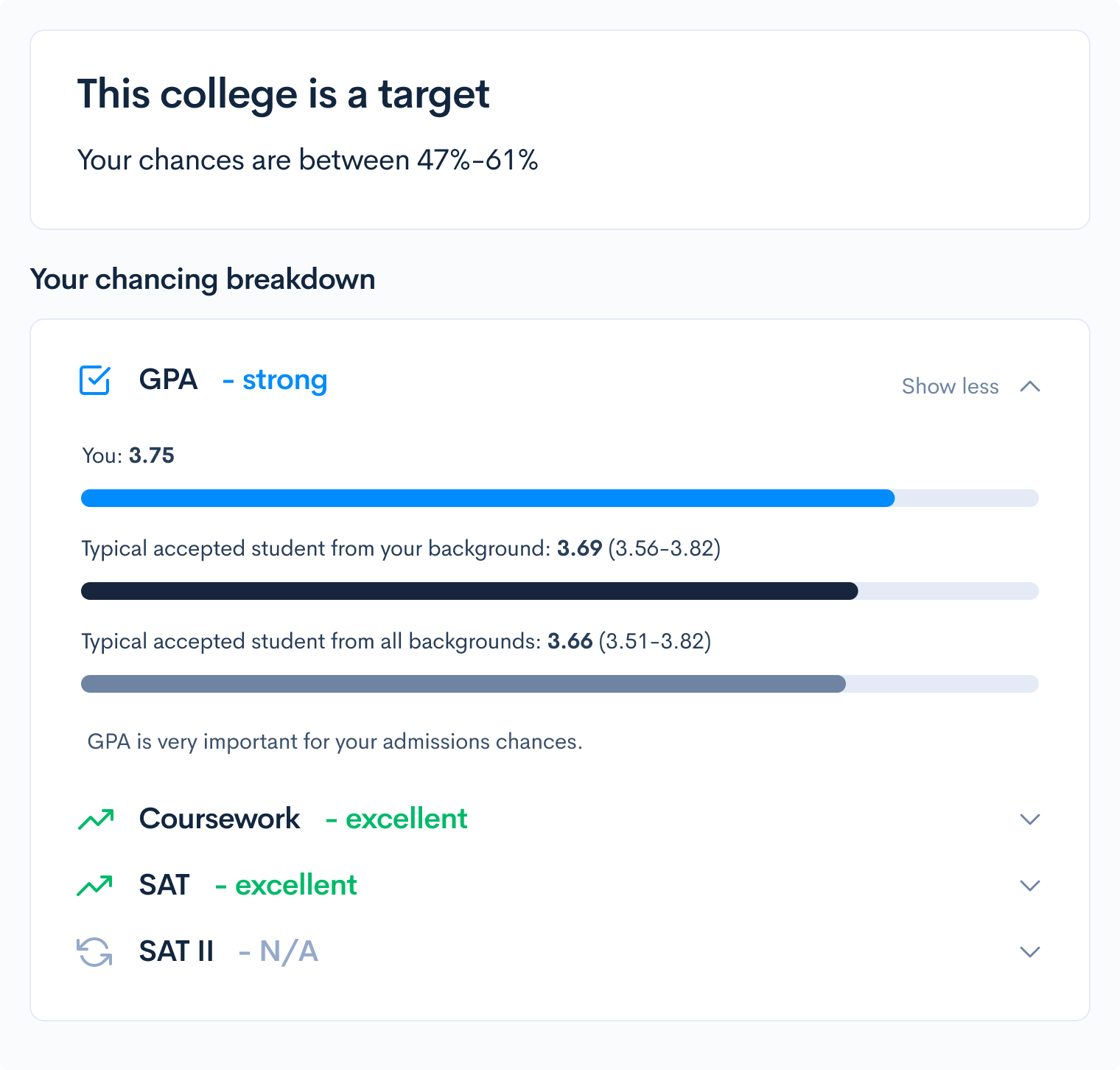
Many selective colleges use a metric called the Academic Index (AI) to assess an application’s strength. The AI is calculated based on GPA and SAT/ACT scores, so you should make sure your scores are competitive to increase your chances of admission. Some colleges even automatically reject applicants with AIs that are too low.

To see how your SAT score compares, use CollegeVine’s free Admissions Chances Calculator . This tool will let you know the impact of your SAT score on your chances and will even offer advice to improve other aspects of your profile.

Strategies to Solve Problem Solving and Data Analysis Problems

Problem Solving and Data Analysis problems often involve graphs or data tables, so it’s important to pay attention to titles and labels to make sure you don’t misinterpret the information. 

As you read the question, underline or circle any important numeric information. Also, pay close attention to what exactly the question is asking for.

Because Problem Solving and Data Analysis problems vary, there is no concrete algorithm to approach them. These questions are typically more conceptual than calculation-based, so though a calculator is allowed, you probably won’t need it aside from simple arithmetic. Therefore, the key to these problems is reading carefully and knowing concepts like proportions, median, mean, percent increase, etc.

10 Difficult Problem Solving and Data Analysis Questions

Here are some sample difficult Problem Solving and Data Analysis questions and explanations of how to solve them. Remember, these questions only appear on the Calculator section of the exam, so you will have access to a calculator for all of them.

1. Measures of Central Tendency (Mean/Median/Mode)

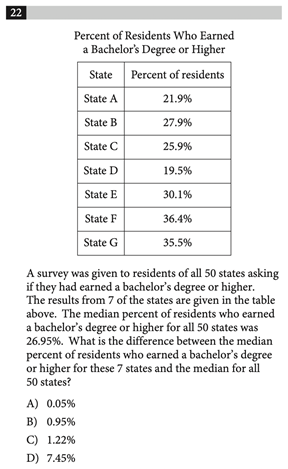
Correct Answer: B

This problem involves computing the median. If you have a graphing calculator, this could be done via lists, but since there are only 7 data values, it might be faster to just write this one out. The median is the measure of the middle of the data set, so start by ordering the values from smallest to largest. This results in the following list: 19.5%, 21.9%, 25.9%, 27.9%, 30.1%, 35.5%, 36.4%. From here, we can clearly see that the middle value is 27.9%, so that is our median. 

However, we’re not done here. We now have to compute the difference between the median we just calculated and the median for all 50 states, 26.95%. Subtracting these two values yields 0.95%, which corresponds to answer choice B. 

2. Percent Increase

Percent increase can be a tricky concept if you don’t remember this rule of thumb: “new minus old over old.” In this case, for the percent increase from 2012 to 2013, we take the “new” value, 5,880, and subtract the “old” value, 5,600. This is 280, which we then divide by the “old” to get .05, which is 5%. 

Since the percent increase from 2012 to 2013 was 5%, and this is double the predicted increase from 2013 to 2014, we know that the percent increase from 2013 to 2014 will be half of 5%, or 2.5%.

Then, to calculate the number of subscriptions sold in 2014, we multiply the value in 2013, 5,880, by 2.5%. This yields 147, which means that in 2014, 147 additional subscriptions were sold. So, the total amount of subscriptions sold in 2014 is 5,880 + 147 = 6,027.

3. Analyzing Graphical Data

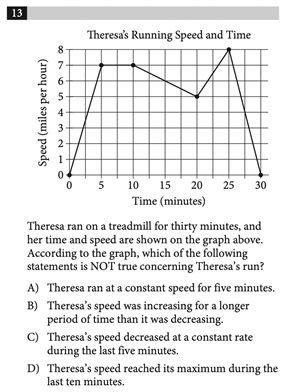
Since we are presented with a graph, let’s make note of what this graph is showing us. On the y-axis we have speed, and on the x-axis we have time. So, this graph is showing us how Theresa’s speed varies with time. 

When the graph is flat, the speed is unchanging and is therefore constant. When the graph has a positive slope, the speed is increasing, and when the graph has a negative slope, the speed is decreasing. The rates at which it increases and decreases will be constant since the graph is composed of straight lines (and a line has a constant slope, which means it changes at a constant rate).

For questions asking which statement is not true, it’s crucial to take the time to read through each answer choice. First, choice A states that Theresa ran at a constant speed for five minutes. We can see that this is true, since from 5 to 10 minutes, the graph is flat. Next, choice C says that the speed decreased at a constant rate during the last five minutes. This is also true because from 25 to 30 minutes, the graph is a line with negative slope, which indicates decreasing speed. Finally, choice D claims the maximum speed occurs during the last 10 minutes. We can see that the maximum speed (the highest point on the graph) occurs at 25 minutes, which is within the last 10 minutes, so choice D is also true.

By process of elimination, choice B should be correct, but let’s verify. Choice B states that Theresa’s speed was increasing for a longer time than it was decreasing. Speed was increasing from 0 to 5 and 20 to 25 minutes, for a total of 10 minutes. Speed was decreasing from 10 to 20 and 25 to 30 minutes, for a total of 15 minutes. So, the speed decreased for a longer time than it increased, and choice B is false, making it the correct answer.

4. Inference

Correct Answer: D

For questions involving surveys, always remember that generalizations can only be made to the specific population studied. For example, if a study is given to a select group of 5th grade math students, when analyzing the results, you can only generalize to 5th grade math students, not all math students or all 5th graders. 

In this case, the group surveyed was people who liked the book. From these people, 95% disliked the movie. So, from this survey, most people who like the book will then dislike the movie, which corresponds to choice D.

Choices A and C are incorrect since they generalize to people who see movies and people who dislike the book, which doesn’t apply to the population studied. Choice B is incorrect since it falsely generalizes to all people who read books.

5. Proportions

Proportion problems are usually fairly quick, but easy to mess up on if not read carefully. For proportions, the denominator is the total number of things in the group we’re looking at, and the numerator is the specific characteristic we want. 

This question asks for the fraction of the dogs that are fed only dry food. So, the group we’re looking at is “dogs” and the characteristic we want is that they “are fed only dry food.” 

From the table, the total number of dogs is 25. This means the denominator will be 25. Next, we must find the number of dogs which are also only fed dry food, which is 2, according to the table. So, our numerator is 2, and the answer is 2/25.

Discover your chances at hundreds of schools

Our free chancing engine takes into account your history, background, test scores, and extracurricular activities to show you your real chances of admission—and how to improve them.

6. Scale Factors

For this question, let’s start with what we know: the column is 8 inches tall. We know that 50 coins creates a \(3\frac{7}{8}\) inch column, which is approximately 4 inches. Since this question asks for an approximation, we know that 8 is slightly more than double \(3\frac{7}{8}\), so we’ll need slightly more than \(50\:\cdot\: 2\) pennies to create an 8-inch column. Answer B is the closest number to our approximate value.

If you wanted to be precise, you could set up an equation:

\(8 in\:\cdot\:\frac{50 coins}{3\frac{7}{8} in}\)

Because 50 coins corresponds to a column which is \(3\frac{7}{8}\) inches tall, we set those two values up in a fraction. We decide which value goes in the numerator and which in the denominator based on the units: since we started with 8 inches, we need the \(3\frac{7}{8}\) inches to be in the denominator so that the inches cancel. Then, we are left with the unit in the numerator, which is coins. The question asks for the number of coins, so this is exactly what we want.

At this point, you would use your calculator to solve the expression, and get about 103 coins. This value is closest to answer choice B.

7. Line of Best Fit/Scatterplots

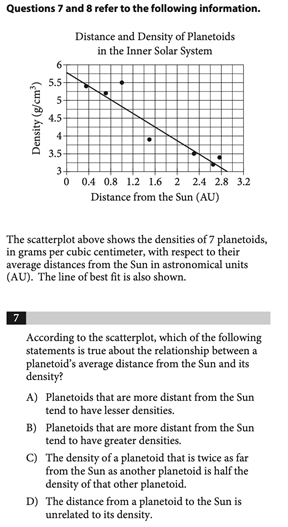
Correct Answer: A

Once again, since we have a graph, let’s take a moment to read the labels. The y-axis shows density and the x-axis shows distance from the sun.

We also see that the line of best fit is sloping downwards. As the distance increases, the density seems to decrease. So, choice A is correct in that larger distances correspond to lesser densities.

Though it wasn’t explicit in this question, an important thing to note about scatterplots is that these relationships show correlation, not causation. Choice C is incorrect because it falsely implies that changes in distance cause changes in density. Choice D is incorrect since though there is no cause and effect relationship, there is a correlation between these two variables.

8. Geometric Applications of Proportions

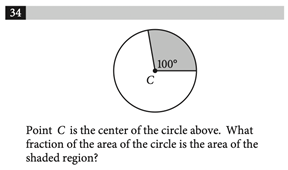
Correct Answer: 5/18, .277, .278

This problem could be confusing in that so little information is given. However, this problem requires that you recall that the proportion of degrees is equivalent to the proportion of area. So, for this problem, all you have to do is divide 100 by 360, which is the total number of degrees in a circle.

Then, the answer is 100/360, or 5/18. If you’re faced with a similar problem on the test, where there is little to no numeric information, try to work with the numbers you do have and find helpful relationships.

9. Unit Conversions

Correct Answer: 195

Unit conversions are fairly simple once you set up the expression correctly. Start with the information given.

For this problem, the price is $62,400, so we will start with this value. Next, we will multiply this value by fractions. Each fraction will consist of a numerator and denominator which are equivalent, so multiplying by these fractions is the same as multiplying by 1. Here is what the expression would look like:

\(\$62,400\:\cdot\:\frac{1 ounce}{\$20}\:\cdot\:\frac{1 pound}{16 ounces}\)

We decide which value to put in the denominator based on the units. In this case, the dollars and the ounces cancel, leaving us with pounds, which is what the question asked for. Solving this expression results in 195 pounds, the answer to the question. 

10. Probability

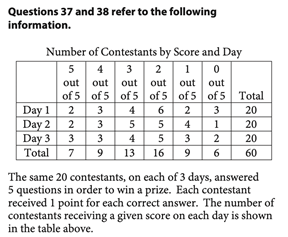
Correct Answer: 5/7, .714

Probability questions are similar to proportion questions in that the denominator should be the group we’re looking at and the numerator should be the characteristic we want.

In this case, it is given that we’re looking at contestants who received a score of 5 on one of the three days, and there is a total of 7 such contestants. The characteristic we want is that the contestant received a score of 5 on Day 2 or Day 3. The number of contestants who fit this description is 2 + 3 = 5, so the probability is 5/7.

For Problem Solving and Data Analysis problems, make sure that your answer addresses what the question asked for. Wrong answer choices on the SAT often reflect common student mistakes, so take the time to read Problem Solving and Data Analysis questions carefully.

When studying for the SAT Math section, try to do plenty of practice problems. The best way to get better at math is to do more math.

Here are some other articles that will help you prepare for the SAT Math section:

• 15 Hardest SAT Math Questions
• 30 SAT Math Formulas You Need to Know
• Guide to SAT Math Heart of Algebra + Practice Questions
• 5 Common SAT Math Mistakes to Avoid
• 5 Tips to Boost Your Math SAT Score

Related CollegeVine Blog Posts

• Math for Kids
• Parenting Resources
• ELA for Kids
• Teaching Resources

How to Teach Number Formation in 5 Easy Steps

13 Best Resources for Math Videos for Kids: Math Made Fun

How to Teach Skip Counting to Kids in 9 Easy Steps

10 Best Math Intervention Strategies for Struggling Students

How to Teach Division to Kids in 11 Easy Steps

How to Cope With Test Anxiety in 12 Easy Ways

Developmental Milestones for 4 Year Olds: The Ultimate Guide

Simple & Stress-Free After School Schedule for Kids of All Ages

When Do Kids Start Preschool: Age & Readiness Skills

Kindergarten Readiness Checklist: A Guide for Parents

How to Teach Letter Formtaion to Kids in 9 Easy Steps

15 Best Literacy Activities for Preschoolers in 2024

12 Best Poems About Teachers Who Change Lives

6 Effective Ways to Improve Writing Skills

40 Four Letter Words That Start With A

60 Fun Animal Facts for Kids

12 Best Behavior Management Techniques for the Classroom

13 Best Online Teaching Tips for Teachers

How to Teach Kids to Write in 9 Easy Steps

13 Challenges for Teachers and How to Address Them

10 Best Strategies for Solving Math Word Problems

1. Understand the Problem by Paraphrasing

2. identify key information and variables, 3. translate words into mathematical symbols, 4. break down the problem into manageable parts, 5. draw diagrams or visual representations, 6. use estimation to predict answers, 7. apply logical reasoning for unknown variables, 8. leverage similar problems as templates, 9. check answers in the context of the problem, 10. reflect and learn from mistakes.

Have you ever observed the look of confusion on a student’s face when they encounter a math word problem ? It’s a common sight in classrooms worldwide, underscoring the need for effective strategies for solving math word problems . The main hurdle in solving math word problems is not just the math itself but understanding how to translate the words into mathematical equations that can be solved.

SplashLearn: Most Comprehensive Learning Program for PreK-5

SplashLearn inspires lifelong curiosity with its game-based PreK-5 learning program loved by over 40 million children. With over 4,000 fun games and activities, it’s the perfect balance of learning and play for your little one.

Generic advice like “read the problem carefully” or “practice more” often falls short in addressing students’ specific difficulties with word problems. Students need targeted math word problem strategies that address the root of their struggles head-on. 

A Guide on Steps to Solving Word Problems: 10 Strategies 

One of the first steps in tackling a math word problem is to make sure your students understand what the problem is asking. Encourage them to paraphrase the problem in their own words. This means they rewrite the problem using simpler language or break it down into more digestible parts. Paraphrasing helps students grasp the concept and focus on the problem’s core elements without getting lost in the complex wording.

Original Problem: “If a farmer has 15 apples and gives away 8, how many does he have left?”

Paraphrased: “A farmer had some apples. He gave some away. Now, how many apples does he have?”

This paraphrasing helps students identify the main action (giving away apples) and what they need to find out (how many apples are left).

Play these subtraction word problem games in the classroom for free:

Students often get overwhelmed by the details in word problems. Teach them to identify key information and variables essential for solving the problem. This includes numbers , operations ( addition , subtraction , multiplication , division ), and what the question is asking them to find. Highlighting or underlining can be very effective here. This visual differentiation can help students focus on what’s important, ignoring irrelevant details.

• Encourage students to underline numbers and circle keywords that indicate operations (like ‘total’ for addition and ‘left’ for subtraction).
• Teach them to write down what they’re solving for, such as “Find: Total apples left.”

Problem: “A classroom has 24 students. If 6 more students joined the class, how many students are there in total?”

Key Information:

• Original number of students (24)
• Students joined (6)
• Looking for the total number of students

Here are some fun addition word problems that your students can play for free:

The transition from the language of word problems to the language of mathematics is a critical skill. Teach your students to convert words into mathematical symbols and equations. This step is about recognizing keywords and phrases corresponding to mathematical operations and expressions .

Common Translations:

• “Total,” “sum,” “combined” → Addition (+)
• “Difference,” “less than,” “remain” → Subtraction (−)
• “Times,” “product of” → Multiplication (×)
• “Divided by,” “quotient of” → Division (÷)
• “Equals” → Equals sign (=)

Problem: “If one book costs $5, how much would 4 books cost?”

Translation: The word “costs” indicates a multiplication operation because we find the total cost of multiple items. Therefore, the equation is 4 × 5 = $20

Complex math word problems can often overwhelm students. Incorporating math strategies for problem solving, such as teaching them to break down the problem into smaller, more manageable parts, is a powerful approach to overcome this challenge. This means looking at the problem step by step rather than simultaneously trying to solve it. Breaking it down helps students focus on one aspect of the problem at a time, making finding the solution more straightforward.

Problem: “John has twice as many apples as Sarah. If Sarah has 5 apples, how many apples do they have together?”

Steps to Break Down the Problem:

Find out how many apples John has: Since John has twice as many apples as Sarah, and Sarah has 5, John has 5 × 2 = 10

Calculate the total number of apples: Add Sarah’s apples to John’s to find the total,  5 + 10 = 15

By splitting the problem into two parts, students can solve it without getting confused by all the details at once.

Explore these fun multiplication word problem games:

Diagrams and visual representations can be incredibly helpful for students, especially when dealing with spatial or quantity relationships in word problems. Encourage students to draw simple sketches or diagrams to represent the problem visually. This can include drawing bars for comparison, shapes for geometry problems, or even a simple distribution to better understand division or multiplication problems .

Problem: “A garden is 3 times as long as it is wide. If the width is 4 meters, how long is the garden?”

Visual Representation: Draw a rectangle and label the width as 4 meters. Then, sketch the length to represent it as three times the width visually, helping students see that the length is 4 × 3 = 12

Estimation is a valuable skill in solving math word problems, as it allows students to predict the answer’s ballpark figure before solving it precisely. Teaching students to use estimation can help them check their answers for reasonableness and avoid common mistakes.

Problem: “If a book costs $4.95 and you buy 3 books, approximately how much will you spend?”

Estimation Strategy: Round $4.95 to the nearest dollar ($5) and multiply by the number of books (3), so 5 × 3 = 15. Hence, the estimated total cost is about $15.

Estimation helps students understand whether their final answer is plausible, providing a quick way to check their work against a rough calculation.

Check out these fun estimation and prediction word problem worksheets that can be of great help:

When students encounter problems with unknown variables, it’s crucial to introduce them to logical reasoning. This strategy involves using the information in the problem to deduce the value of unknown variables logically. One of the most effective strategies for solving math word problems is working backward from the desired outcome. This means starting with the result and thinking about the steps leading to that result, which can be particularly useful in algebraic problems.

Problem: “A number added to three times itself equals 32. What is the number?”

Working Backward:

Let the unknown number be x.

The equation based on the problem is  x + 3x = 32

Solve for x by simplifying the equation to 4x=32, then dividing by 4 to find x=8.

By working backward, students can more easily connect the dots between the unknown variable and the information provided.

Practicing problems of similar structure can help students recognize patterns and apply known strategies to new situations. Encourage them to leverage similar problems as templates, analyzing how a solved problem’s strategy can apply to a new one. Creating a personal “problem bank”—a collection of solved problems—can be a valuable reference tool, helping students see the commonalities between different problems and reinforcing the strategies that work.

Suppose students have solved a problem about dividing a set of items among a group of people. In that case, they can use that strategy when encountering a similar problem, even if it’s about dividing money or sharing work equally.

It’s essential for students to learn the habit of checking their answers within the context of the problem to ensure their solutions make sense. This step involves going back to the original problem statement after solving it to verify that the answer fits logically with the given information. Providing a checklist for this process can help students systematically review their answers.

Checklist for Reviewing Answers:

• Re-read the problem: Ensure the question was understood correctly.
• Compare with the original problem: Does the answer make sense given the scenario?
• Use estimation: Does the precise answer align with an earlier estimation?
• Substitute back: If applicable, plug the answer into the problem to see if it works.

Problem: “If you divide 24 apples among 4 children, how many apples does each child get?”

After solving, students should check that they understood the problem (dividing apples equally).

Their answer (6 apples per child) fits logically with the number of apples and children.

Their estimation aligns with the actual calculation.

Substituting back 4×6=24 confirms the answer is correct.

Teaching students to apply logical reasoning, leverage solved problems as templates, and check their answers in context equips them with a robust toolkit for tackling math word problems efficiently and effectively.

One of the most effective ways for students to improve their problem-solving skills is by reflecting on their errors, especially with math word problems. Using word problem worksheets is one of the most effective strategies for solving word problems, and practicing word problems as it fosters a more thoughtful and reflective approach to problem-solving

These worksheets can provide a variety of problems that challenge students in different ways, allowing them to encounter and work through common pitfalls in a controlled setting. After completing a worksheet, students can review their answers, identify any mistakes, and then reflect on them in their mistake journal. This practice reinforces mathematical concepts and improves their math problem solving strategies over time.

3 Additional Tips for Enhancing Word Problem-Solving Skills

Before we dive into the importance of reflecting on mistakes, here are a few impactful tips to enhance students’ word problem-solving skills further:

1. Utilize Online Word Problem Games

Incorporate online games that focus on math word problems into your teaching. These interactive platforms make learning fun and engaging, allowing students to practice in a dynamic environment. Games can offer instant feedback and adaptive challenges, catering to individual learning speeds and styles.

Here are some word problem games that you can use for free:

2. Practice Regularly with Diverse Problems

Consistent practice with a wide range of word problems helps students become familiar with different questions and mathematical concepts. This exposure is crucial for building confidence and proficiency.

Start Practicing Word Problems with these Printable Word Problem Worksheets:

3. Encourage Group Work

Solving word problems in groups allows students to share strategies and learn from each other. A collaborative approach is one of the best strategies for solving math word problems that can unveil multiple methods for tackling the same problem, enriching students’ problem-solving toolkit.

Conclusion 

Mastering math word problems is a journey of small steps. Encourage your students to practice regularly, stay curious, and learn from their mistakes. These strategies for solving math word problems are stepping stones to turning challenges into achievements. Keep it simple, and watch your students grow their confidence and skills, one problem at a time.

Frequently Asked Questions (FAQs)

How can i help my students stay motivated when solving math word problems.

Encourage small victories and use engaging tools like online games to make practice fun and rewarding.

What's the best way to teach beginners word problems?

Begin with simple problems that integrate everyday scenarios to make the connection between math and real-life clear and relatable.

How often should students practice math word problems?

Regular, daily practice with various problems helps build confidence and problem-solving skills over time.

Most Popular

15 Best Report Card Comments Samples

117 Best Riddles for Kids (With Answers)

40 best good vibes quotes to brighten your day, recent posts.

10 Best Online Homeschool Programs

12 Best Activities for Kinesthetic Learners

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Choose Your Test

Sat / act prep online guides and tips, problem solving and data analysis: key sat math concepts.

SAT Math is divided intro three domains:

• Heart of Algebra
• Problem Solving and Data Analysis
• Passport to Advanced Math

It's a good idea to get really familiar with what's going to be on the test, where it was derived, and what the SAT is really testing.

This post will focus on one domain— Problem Solving and Data Analysis . This is an opportunity to get cozy with these concepts, and with the overall tapes of information that test-makers are looking for. Problem Solving and Data Analysis problems are all about applying your math knowledge to practical situations and looking at actual statistics instead of abstract, theoretical scenarios.

Basic Information

There are 17 questions in this domain (out of 58 total math questions). They aren't labeled or otherwise indicated on the test— you're never told which type of question you're working on.

There are no Problem Solving and Data Analysis problems on the no-calculator section. You will always be permitted to use your approved calculator for questions from this domain —though you may not always need it.

You will receive a subscore on a scale of 1-15 on this domain.

There will be both multiple choice and grid-in questions.

You'll be dealing with both single-step and multistep problems; sometimes, it's just a matter of reading the data and parroting it back, while other problems require a bit more manipulation of the numbers.

General Concepts

The test-makers want to know that you understand math thoroughly enough to use your skills in real-world settings .

Quantitative reasoning is also crucial; you should be able to work with numbers and draw conclusions about what they imply.

You’ll be working with a lot of numbers.

Real-World Applications

You should be able to build a representation of a problem. If a scenario is described to you, you should be able to model it mathematically by describing it with expressions and equations.

You should know to consider the units involved. If there happens to be a shift of units (from feet to miles, or something like that), you should account for that as you calculate.

You should keep track of the practical meaning of quantities . You're going to be representing real values with variables: don't forget what those variables represent. Also, be sure you understand how a change in one of these variables or quantities affects what's happening in the equation. For example, in a line ($y=mx+b$) with a positive slope (or value of $m$), increasing $x$ will also result in an increase in $y$.

Data and Statistics

There are a lot of graphs, charts, and tables that could be covered on the test. You should be capable of analyzing one-variable data in bar graphs, histograms, line graphs, and box-and-whisker plots—as well as two-variable data in scatterplots and two-way tables. In other words, you should be fluent in reading these various representations of data.

You should be able to describe overall patterns. You'll have to identify positive and negative trends. You should be able to distinguish between linear and exponential growth.

Specific Skills

There are a number of skills that you'll want to be handy with on the day of the exam. In this section you'll find a discussion of these skills, including what they are and what they look like in action.

In fact, let’s hope these skills aren’t all that new!

Statistical Analysis

The measures of center are arithmetic mean (average) and median. If they can't be calculated from what's given, you may still need to draw some conclusions about them. Even if you can't find the actual number, there may be a question about what possible values are, or how the values compare to another set of data. Outliers typically affect the mean, but not the median.

The measure of spread to know is standard deviation. You've got to have the basic theory, but you won't need to calculate the exact value. You should be able to look at two sets of data and see which set is more spread out—that is, which has the greater standard deviation.

Insofar as the precision of estimates is concerned, everything depends on the variability of the data and the sample size; smaller variability combined with a larger sample size makes for estimates that are more precise in terms of the actual population.

Another tidbit of interest you should know is that randomization combats bias .

You should, in context, be able to work with margins of error, which are affected by sample size and standard deviation.

Confidence intervals should also be taken into account. The SAT always works with confidence intervals of 95%. This doesn’t mean that 95% of the population is necessarily described by the figure that’s been derived, just that we can be 95% certain that the descriptive figure that’s been reached is accurate.

When analyzing the relationship between two variables, remember, correlation is not causation. If subjects for a sample are selected randomly, we can generalize to the entire population reasonably well. If subjects are randomly assigned to test groups, we can reasonably speculate about cause and effect. Otherwise, though, we’re out of luck.

You should also be able to evaluate reports to make inferences, justify conclusions, and determine the appropriateness of data collection methods .

Take a look at this problem:

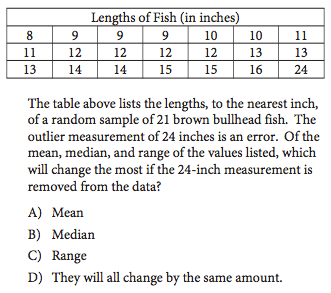
The correct answer here is (C). We know that removing one very high number from the set is not going to affect the median—the middle three values are all 12, so we know the median will still be 12, even if the middle of the data is shifted over one. The mean will shift somewhat if we don’t include the 24-inch measurement, but there are 20 other data points that anchor the mean at a relatively consistent value if any one value is removed. The range, however, will change from $24-8=16$ to $16-8=8$. The range gets cut in half if we remove the 24-inch measurement! That’s the measure that will change the most.

Mathematical Models

The domain of the SAT that we’re examining gives special attention to mathematical models. You must, therefore, be able to create and use a model.

When two variables are presented in a graph, table, or other chart , you should be handy with analyzing and drawing conclusions with regards to the relationship between these variables.

Relationships between variables can be modeled by functions, but remember the function is only a model! It may give scientifically accurate predictions, or it may just describe a general trend. You may be asked whether a model is good, acceptable, or entirely inappropriate.

Let’s look at this problem:

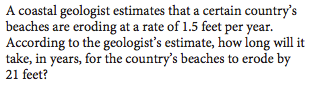
The geologist in the question provides a model regarding the country’s beach erosion. According to that model, beaches erode at a rate of 1.5 feet per year. 21 feet of erosion would therefore take 14 years, as $14(1.5)=21$.

The functions you’re asked to work with may be linear, quadratic, and/or exponential. Linear and exponential are discussed in more detail below.

An important example of linear growth is simple interest , where you earn interest on your principal, each period, but not on any interest that has been added since that first deposit. This is modeled by the function: $A = P(1+rt)$. $P$ is the principal, $r$ is the interest rate, and $t$ is the amount of time interest has been accruing.

Exponential

An important example of exponential growth is compound interest , where you earn interest on the interest you’ve previously earned. This is modeled by the function: $A = P (1+r/n)^{nt}$, where $P$ is the principal, $r$ is the interest rate (typically annual), $n$ is the number of times the interest compounds per period (typically a year), and $t$ is the amount of time that has passed since the principal began accruing interest.

Be careful! The stated rate of change may not be the same as the rate of change over time. This is typical of compound interest:

• You might take a loan at 9%, but if it compounds monthly, you’re really taking a loan at $(1+.09/12)^12 – 1 = 9.38%$ at the end of the year.
• On the other hand, you might make a deposit that accrues interest at a rate of 5%, but it compounds quarterly, so you’re really getting $(1+.05/4)^4 – 1 = 5.095%$ at the end of the year.

Math and money are very closely linked.

Ratios, Proportions, Units, and Percentages

You’ll need to be familiar with direct proportionality/variation : $y = kx$, where $k$ is a unitless constant of proportion. This relationship may also be expressed as $x_1/y_1 = x_2/y_2$.

You’ll need to know how percent increase and percent decrease work. Be careful about how you approach these problems; they can get a little tricky. Remember, for instance, that if you have a 20%-off coupon for an item that’s on a 20%-off sale, you won’t save 40%. You’ll save 36%, as you’ll pay 80% of 80% of the original price: $x(.8)(.8) = (.64)x = x - (.36)x$.

Take a look at this pair of problems:

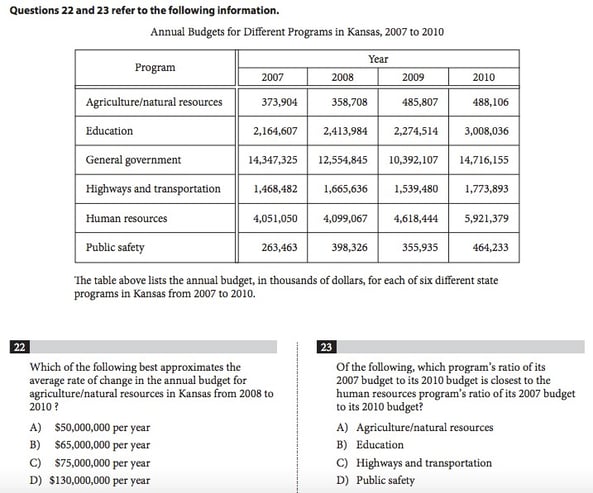
This is the sort of situation where you’re asked to deal with quantities in very practical terms. These aren’t just numbers floating in and out of an abstract function ; no, these numbers represent that annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.

The first problem is asking for the approximate average rate of change in the annual budget for agriculture/natural resources in Kansas from 2008 to 2010. From 2008 to 2009, the budget grew by 127,099 thousands of dollars, or $127,099,000. From 2009 to 2010, the budget grew by 2,299 thousands of dollars, or $2,299,000. Thus, we add those two figures together, divide by two, and find that the average growth was $64,699,000, or, when rounding, (B).

For the next problem, we are comparing the 2007-budget-to-2010-budget ratios across the various programs. We will first need to find those ratios:  

Agriculture/natural resources — $373,904/488,106=.766$

Education — $2,164,607/3,008,036=.7196$

Highways and transportation — $1,468,482/1,773,893=.8278$

Public safety — $263,463/464,233=.5675$

Out of these, the closest to human resources ($4,051,050/5,921,379=.6841$), is (B).

• Probability

Two events are independent if one happening has nothing to do with another , like the sun shining and you eating a sandwich for lunch. The sun may shine, and you may eat a sandwich for lunch, but one does not cause or prevent the other.

Two events are mutually exclusive if they cannot both occur , like me wearing a hat and me not wearing a hat. I can’t do both.

For independent, non-mutually exclusive events: P(A and B) = P(A)*P(B), whereas P(A or B) = P(A) + P(B) - P(A and B).

For mutually exclusive events: P(A or B) = P(A) + P(B).

There are other formulas for more complicated scenarios, but these will get you pretty far — they’re all you should need on the SAT.

Let’s take a look at this problem:

Twenty-five people passed the bar exam; of these, seven did not take the review course. So, the probability that the interviewed person in question did not take the bar exam is 7/25, or (B).

Math and gambling are closely linked, too. It’s all about that probability.

This domain of the test is calculation-heavy, although there are some theoretical questions.

These questions compose almost a third of the test . They cover, roughly:

• Statistical analysis
• Proportions
• Real-world data

Your answers will be scored to yield one of three subscores for the Math section.

What’s Next?

That was a fair amount of information. Digest it a little; then, a great next stop would be perusing our overall guide to SAT Math , including directions to a number of other great posts .

Now, because Problem Solving and Data Analysis problems are so information-heavy , you may wish to practice with some word problems , to get used to that much verbal data being thrown your way.

As you’re trying these practice problems, you’ll want to know how to use them to your best advantage .

Want to improve your SAT score by 160 points?

Check out our best-in-class online SAT prep program . We guarantee your money back if you don't improve your SAT score by 160 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses . If you liked this Math strategy guide, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.

Check out our 5-day free trial:

Vero is a firsthand expert at standardized testing and the college application process. Though neither parent had graduated high school, and test prep was out of the question, she scored in the 99th percentile on both the SAT and ACT, taking each test only once. She attended Dartmouth, graduating as salutatorian of 2013. She later worked as a professional tutor. She has a great passion for the arts, especially theater.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.6: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 132869

• Michelle Manes
• University of Hawaii

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solve them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching  effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, How to Solve it . Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

A Problem Solving Strategy: Try Something!

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

Note that being "good at mathematics" is not about doing things right the first time. It is about figuring things out. Practice being okay with having done something incorrectly. Try to avoid using an eraser and just lightly cross out incorrect work (do not black out the entire thing). This way if it turns out that you did something useful, you still have that work to reference! If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what was left after paying Brianna. Finally, Alex saw David and gave him 1/2 of the remaining money. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

A Problem Solving Strategy: Draw a Picture

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

A Problem Solving Strategy: Make Up Numbers

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

Try this: Assume (that is, pretend) Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person.

Or try working backward: suppose Alex has some specific amount left at the end, say $10. Since he gave David half of what he had before seeing David, that means he had $20 before running into David. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

Most people want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. Instead of asking the teacher, “Is this right?”, you should be ready to justify it and say, “Here’s my answer, and here is how I got it.”

A Problem Solving Strategy: Try a Simpler Problem

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said, “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

The ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

A Problem Solving Strategy: Work Systematically

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

A Problem Solving Strategy: Use Manipulatives to Help You Investigate

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

A Problem Solving Strategy: Look for and Explain Patterns

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table. If possible, actually describe these to a friend.
• Explain and justify any of the patterns you see (if possible, actually do this with a friend). If you don't have a partner to work with, imagine they asked you, "How can you be sure the patterns will continue?"
• Expand this to find what calculation(s) you would perform to find the total number of squares on a 100 × 100 chess board.

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What progress have you made?

A Problem Solving Strategy: Find the Math, Remove the Context

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

A Problem Solving Strategy: Check Your Assumptions

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

How to analyze students’ logical-mathematical intelligence in problem solving based on SOLO taxonomy

[email protected]

• Split-Screen
• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Open the PDF for in another window
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Khairul Bariyah , Endah Retnowati; How to analyze students’ logical-mathematical intelligence in problem solving based on SOLO taxonomy. AIP Conf. Proc. 29 April 2024; 2622 (1): 080010. https://doi.org/10.1063/5.0133822

Download citation file:

• Ris (Zotero)
• Reference Manager

Various ways and strategies in solving a problem depend on the intelligence level of a person. Eight types of intelligences declared by Gardner, one of them is logical-mathematical intelligence. SOLO taxonomy can be used to analyze students’ logical-mathematical intelligence in solving mathematical problems. It can be analyzed by deciding the logical-mathematical intelligence assessment indicators and the indicators of students’ response levels, classifying students’ development intelligence with the assessment of low interest, consistent growth, and high interest. In addition, the pre-structural, uni-structural, multi-structural, relational, and extended abstract levels have certain characteristics and indicators that can assess the response level of students’ abilities. Domain in this study is the geometry which the topics are perimeter and area of quadrilaterals as one of the TIMSS assessments. The example problem to solve in topic is how to find the area and perimeter of quadrilateral at 8 th grade students of Junior High School. As the result, the teacher can analyze students’ logical-mathematical intelligence base on SOLO taxonomy with its categories. This is a literature review which aim to discuss how literatures might be used to analyze students’ logical-mathematical intelligence in solving mathematical problems based on the SOLO taxonomy when needed in mapping logical-mathematical intelligence assessment indicators and indicators of students’ response levels.

Citing articles via

Publish with us - request a quote.

Sign up for alerts

• Online ISSN 1551-7616
• Print ISSN 0094-243X
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

How two high school students solved a 2,000-year-old math puzzle

Workers get a stake in their company under employee ownership model

Leader Hakeem Jeffries on Israel, House Republicans and the election

Can workers prosper with employee ownership?

An effective computational solver for fractal-fractional 2D integro-differential equations

• Original Research
• Published: 07 May 2024

Cite this article

• P. Rahimkhani 1 ,
• S. Sedaghat 2 &
• Y. Ordokhani   ORCID: orcid.org/0000-0002-5167-6874 3  

In this paper, we develop a computational approach for fractal-fractional integro-differential equations (FFIDEs) in Atangana–Riemann–Liouville sense. This plan focuses on the Chelyshkov polynomials (ChPs) and the utilization of the Legendre–Gauss quadrature rule. The operational matrices (OMs) of integration, integer-order derivative and fractal-fractional-order derivative are calculated. These matrices in comparison to OMs existing in other methods are more accurate. The method consists of approximating the exiting functions in terms of basis functions. Using the provided OMs alongside the Legendre collocation points, the original problem is converted into a set of nonlinear algebraic equations containing unknown parameters. An error analysis is presented to demonstrate the convergence order of the approach. We demonstrate the effectiveness and reliability of the proposed technique by solving numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data Availability

Data will be made available on reasonable request.

Abro, K.A., Atangana, A.: Mathematical analysis of memristor through fractal-fractional differential operators: a numerical study. Math. Methods Appl. Sci. 43 (10), 6378–6395 (2020)

Article   MathSciNet   Google Scholar  

Abro, K.A., Atangana, A.: A comparative study of convective fluid motion in rotating cavity via Atangana–Baleanu and Caputo–Fabrizio fractal-fractional differentiations. Eur. Phys. J. Plus 135 (2), 1–16 (2020)

Article   Google Scholar  

Atangana, A., Khan, M.A.: Modeling and analysis of competition model of bank data with fractal-fractional Caputo-Fabrizio operator. Alex. Eng. J. 59 (4), 1985–1998 (2020)

Wang, W., Khan, M.A.: Analysis and numerical simulation of fractional model of bank data with fractal-fractional Atangana-Baleanu derivative. J. Comput. Appl. Math. 369 , 112646 (2020)

Srivastava, H.M., Saad, K.M.: Numerical simulation of the fractal-fractional Ebola virus. Fractal Fract 4 (4), 1–13 (2020)

Atangana, A., Qureshi, S.: Modeling attractors of chaotic dynamical systems with fractal-fractional operators. Chaos Solitons Fractals 123 , 320–337 (2019)

Abro, K.A., Atangana, A.: Numerical and mathematical analysis of induction motor by means of AB-fractal-fractional differentiation actuated by drilling system. Numerical Methods for Partial Differential Equations 38 (3), 293–307 (2022)

MathSciNet   Google Scholar  

Ahmad, I., Ahmad, N., Shah, K., Abdeljawad, T.: Some appropriate results for the existence theory and numerical solutions of fractals-fractional order malaria disease mathematical model. Results Control Optim. 14 , 100386 (2024)

Shah, K., Abdeljawad, T.: On complex fractal-fractional order mathematical modeling of CO 2 emanations from energy sector. Phys. Scr. 99 (1), 015226 (2023)

Khan, Z.A., Shah, K., Abdalla, B., Abdeljawad, T.: A numerical study of complex dynamics of a chemostat model under fractal-fractional derivative. Fractals 31 (08), 2340181 (2023)

Khan, Z.A., Rahman, M., Shah, K.: Study of a fractal-fractional smoking models with relapse and harmonic mean type incidence rate. J. Funct. Spaces 2021 , 1–11 (2021)

Hosseininia, M., Heydari, M.H., Maalek Ghaini, F.M., Avazzadeh, Z.: A meshless technique based on the moving least squares shape functions for nonlinear fractal-fractional advection-diffusion equation. Engineering Analysis with Boundary Elements 127 , 8–17 (2021)

Hosseininia, M., Heydari, M.H., Avazzadeh, Z.: The numerical treatment of nonlinear fractal-fractional 2D Emden-Fowler equation utilizing 2D Chelyshkov polynomials. Fractals 28 (08), 2040042 (2020)

Dehestani, H., Ordokhani, Y.: Developing the discretization method for fractal-fractional two-dimensional Fredholm–Volterra integro-differential equations. Math. Methods Appl. Sci. 44 (18), 14256–14273 (2021)

Dehestani, H., Ordokhani, Y.: An optimum method for fractal-fractional optimal control and variational problems. Int. J. Dyn. Control. pp. 1–13 (2022)

Shah, K., Sarwar, M., Abdeljawad, Shafiullah, T.: Sufficient criteria for the existence of solution to nonlinear fractal-fractional order coupled system with couple integral boundary conditions. J. Appl. Math. Comput. pp. 1–15 (2024)

Shafiullah, K., Shah, M., Sarwar, T.: Abdeljawad, On theoretical and numerical analysis of fractal-fractional non-linear hybrid differential equations. Nonlinear Eng. 13 (1), 20220372 (2024)

Heydari, M.H.: Numerical solution of nonlinear 2D optimal control problems generated by Atangana-Riemann-Liouville fractal-fractional derivative. Appl. Numer. Math. 150 , 507–518 (2020)

Heydari, M.H., Atangana, A., Avazzadeh, Z.: Numerical solution of nonlinear fractal-fractional optimal control problems by Legendre polynomials. Math. Methods Appl. Sci. 44 (4), 2952–2963 (2021)

Araz, S.I.: Numerical analysis of a new volterra integro-differential equation involving fractal-fractional operators. Chaos Solitons Fractals 130 , 109396 (2020)

Rahimkhani, P., Ordokhani, Y., Sedaghat, S.: The numerical treatment of fractal-fractional 2D optimal control problems by Müntz-Legendre polynomials. Optim. Control Appl. Methods 44 (6), 3033–3051 (2023)

Rahimkhani, P., Heydari, M.H.: Fractional shifted Morgan–Voyce neural networks for solving fractal-fractional pantograph differential equations. Chaos Solitons Fractals 175 , 114070 (2023)

Meleshko, S. V., Grigoriev, Y. N., Ibragimov, N. K., and Kovalev, V. F.: Symmetries of integro-differential equations: with applications in mechanics and plasma physics. Springer Science and Business Media (2010)

Mashayekhi, S., Sedaghat, S.: Fractional model of stem cell population dynamics. Chaos Solitons Fractals 146 , 110919 (2021)

Medlock, J., Kot, M.: Spreading disease: integro-differential equations old and new. Math. Biosci. 184 (2), 201–222 (2003)

Rahimkhani, P., Ordokhani, Y., Babolian, E.: Fractional-order Bernoulli functions and their applications in solving fractional Fredholem-Volterra integro-differential equations. Appl. Numer. Math. 122 , 66–81 (2017)

Rahimkhani, P., Ordokhani, Y.: Hahn wavelets collocation method combined with Laplace transform method for solving fractional integro-differential equations. Math. Sci. (2023). https://doi.org/10.1007/s40096-023-00514-3

Khader, M.M., Sweilam, N.H.: On the approximate solutions for system of fractional integro-differential equations using Chebyshev pseudo-spectral method. Appl. Math. Model. 37 , 9819–9828 (2013)

Saadatmandi, A., Dehghan, M.: A Legendre collocation method for fractional integro-differential equations. J. Vib. Control 17 (13), 2050–2058 (2011)

Nemati, S., Sedaghat, S., Mohammadi, I.: A fast numerical algorithm based on the second kind Chebyshev polynomials for fractional integro-differential equations with weakly singular kernels. J. Comput. Appl. Math. 308 , 231–242 (2016)

Nemati, S., Lima, P.M., Sedaghat, S.: Legendre wavelet collocation method combined with the Gauss Jacobi quadrature for solving fractional delay-type integro-differential equations. Appl. Numer. Math. 149 , 99–112 (2020)

Rahimkhani, P., Ordokhani, Y.: Approximate solution of nonlinear fractional integro-differential equations using fractional alternative Legendre functions. J. Comput. Appl. Math. 365 , 112365 (2020)

Doha, E., Abdelkawy, M., Amin, A., Baleanu, D.: Spectral technique for solving variable-order fractional Volterra integro-differential equations. Numer. Methods Partial Differ. Equ. 34 (5), 1659–1677 (2018)

Chelyshkov, V.S.: Alternative orthogonal polynomials and quadratures. Electron. Trans. Numer. Anal. 25 (7), 17–26 (2006)

Talaei, Y., Asgari, M.: An operational matrix based on Chelyshkov polynomials for solving multi-order fractional differential equations. Neural Comput. Appl. 30 (5), 1369–1376 (2018)

Moradi, L., Mohammadi, F., Baleanu, D.: A direct numerical solution of time-delay fractional optimal control problems by using Chelyshkov wavelets. J. Vib. Control 25 (2), 310–324 (2019)

Rahimkhani, P., Ordokhani, Y.: Chelyshkov least squares support vector regression for nonlinear stochastic differential equations by variable fractional Brownian motion. Chaos Solitons Fractals 163 , 112570 (2022)

Rahimkhani, P., Ordokhani, Y., Lima, P.M.: An improved composite collocation method for distributed-order fractional differential equations based on fractional Chelyshkov wavelets. Appl. Numer. Math. 145 , 1–27 (2019)

Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol 204. Elsevier (2006)

Granas, A., Dugundji, J.: Elementary fixed point theorems. In: Fixed Point Theory, Berlin: Springer, pp. 9–84 (2003)

Rahimkhani, P., Ordokhani, Y.: Numerical solution a class of 2D fractional optimal control problems by using 2D Müntz-Legendre wavelets. Optim. Control Appl. Methods 39 (6), 1916–1934 (2018)

Canuto, C., Hussaini, M., Quarteroni, A., Zang, T.A.: Spectral Methods: Fundamentals in Single Domains. Springer, Berlin (2006)

Book   Google Scholar  

Kreyszig, E.: Introductory Functional Analysis with Applications. Wiley (1991)

Andrews, G. E., Askey, R., Roy, R.: Special functions. Encyclopedia of Mathematics and its Applications Vol 71. Cambridge University Press (1999)

Download references

Acknowledgements

We express our sincere thanks to the anonymous referees for valuable suggestions that improved the paper.

Author information

Authors and affiliations.

Faculty of Science, Mahallat Institute of Higher Education, Mahallat, Iran

P. Rahimkhani

Department of Mathematics, Buein Zahra Technical University, Buein Zahra, Qazvin, Iran

S. Sedaghat

Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

Y. Ordokhani

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Y. Ordokhani .

Ethics declarations

Conflict of interest.

The authors wish to confirm that there are no known Conflict of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Rahimkhani, P., Sedaghat, S. & Ordokhani, Y. An effective computational solver for fractal-fractional 2D integro-differential equations. J. Appl. Math. Comput. (2024). https://doi.org/10.1007/s12190-024-02099-z

Download citation

Received : 07 March 2024

Revised : 16 April 2024

Accepted : 18 April 2024

Published : 07 May 2024

DOI : https://doi.org/10.1007/s12190-024-02099-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Fractal-fractional integro-differential equations
• Mittag–Leffler kernel
• Operational matrix
• Chelyshkov polynomials
• Convergence analysis.

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

New Orleans teens solve 2,000-year-old math problem

W hen she started a math contest with a bonus question challenging students to create a new proof for the Pythagorean theorem using trigonometry, teacher Michelle Blouin Williams didn’t expect anyone to complete the task.

“I was just looking for some ingenuity,” she said, per CBS News .

Calcea Johnson and Ne’Kiya Jackson, however, blew Williams’ expectations out of the water by figuring it out in 2023. The teens were seniors at St. Mary’s Academy in New Orleans, a prestigious Catholic school for girls which has maintained a 100% acceptance rate to colleges and 100% graduation rate for 17 years, CBS News reported.

They appeared in an episode of CBS News’ “60 Minutes ” on Sunday to talk about their achievement.

How did the teens find the answer?

While they were motivated initially by the math competition’s $500 prize, an internal drive to finish what they started manifested when they reached the tricky bonus question. For two months, the high school seniors worked tirelessly to finish their proof.

CeCe Johnson, Calcea’s mother, told “60 Minutes,” “It was pages and pages and pages of, like, over 20 or 30 pages for this one problem.”

Her father, Cal Johnson, added, “Yeah, the garbage can was full of papers, which she would, you know, work out the problems and — if that didn’t work she would ball it up, throw it in the trash.”

When they finished, teachers at St. Mary’s recognized the importance of their work and submitted their proof to the American Mathematical Society for recognition at a conference in March 2023, where the students presented their work.

What is the Pythagorean theorem and what’s a proof?

In essence, the mathematical theorem states that knowing the lengths of two sides of a right triangle enables you to figure out the length of the third using this formula: a² + b² = c².

It’s associated with Greek mathematician Pythagoras, but evidence suggests it was known earlier, in Babylon and Iron Age India, per Britannica . Its practical uses include construction and architecture, two-dimensional navigation, and surveying.

A mathematical proof is exactly what it sounds like: reasoning that proves a mathematical theorem is true. American mathematician Daniel Kane explains proofs as being like essays, but using math.

Why is Calcea Johnson and Ne’Kiya Jackson’s work significant?

According to the “ 60 Minutes ” episode, “there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible.”

In 1927, mathematician Elisha Loomis said as much in his book, “ The Pythagorean Proposition .” Loomis argued that there could be no trigonometric proof of the theorem because it would be circular.

Stuart Anderson, a professor emeritus of mathematics at Texas A&M University–Commerce, told Scientific American , “A lot of the basic trig ‘identities’ are nothing more than Pythagoras’ theorem.”

So, because trigonometric functions are based upon the Pythagorean theorem, using them reflexively to prove the theorem would be akin to going in circles and a fundamental mathematical error, Loomis argued.

According to Scientific American , the teens refuted this in their presentation in 2023 and said that “a trigonometric identity called the law of sines didn’t depend on the Pythagorean theorem and that they could use it to prove the theorem.”

Calcea and Ne’Kiya have joined an extremely small group who’ve accomplished the same feat, including mathematician Jason Zimba, who successfully created a new proof in 2009. The two submitted their proof for final peer review this spring and continue to work on creating more proofs.

How did the world respond to their accomplishment?

The teens were given the keys to the city of New Orleans and a commendation from the governor of Louisiana, among other public recognitions.

While their achievement “blew up,” as Ne’Kiya described it, the two students remain humble, and laughed at being called geniuses.

When news of their accomplishment broke, some people seemed to be shocked and dismissed the news as fake, St. Mary’s president Pamela Rogers said in the interview .

“They were saying, ‘Oh, they could not have done it. African Americans don’t have the brains to do it.’ ... People — have a vision of who can be successful. And — to some people, it is not always an African American female. And to us, it’s always an African American female.”

When interviewer Bill Whitaker asked why they thought there’d been such a response, Ne’Kiya said, “Probably because we’re African American, one. And we’re also women. So I think — oh, and our age. Of course our ages probably played a big part.”

“I’d like to actually be celebrated for what it is. Like, it’s a great mathematical achievement,” she continued.