problem solving proportion

Direct & Inverse Proportions/Variations

Related Pages: Direct Variations Proportion Word Problems More Algebra Lessons

In these lessons, we will learn how to solve direct proportions (variations) and inverse proportions (inverse variations) problems. (Note: Some texts may refer to inverse proportions/variations as indirect proportions/variations.)

The following diagram gives the steps to solve ratios and direct proportion word problems. Scroll down the page for examples and step-by-step solutions.

Printable & Online Ratio & Proportion Worksheets

Direct Proportions/Variations

Knowing that the ratio does not change allows you to form an equation to find the value of an unknown variable.

Example : If two pencils cost $1.50, how many pencils can you buy with $9.00?

How To Solve Directly Proportional Questions?

Example 1: F is directly proportional to x. When F is 6, x is 4. Find the value of F when x is 5. Example 2: A is directly proportional to the square of B. When A is 10, B is 2. Find the value of A when B is 3.

How To Use Direct Proportion?

How To Solve Word Problems Using Proportions?

This video shows how to solve word problems by writing a proportion and solving 1. A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour, how much sugar do I use? 2. A syrup is made by dissolving 2 cups of sugar in 2/3 cups of boiling water. How many cups of sugar should be used for 2 cups of boiling water? 3. A school buys 8 gallons of juice for 100 kids. how many gallons do they need for 175 kids?

Solving More Word Problems Using Proportions

1. On a map, two cities are 2 5/8 inches apart. If 3/8 inches on the map represents 25 miles, how far apart are the cities (in miles)? 2. Solve for the sides of similar triangles using proportions

Inverse Proportions/Variations Or Indirect Proportions

Two values x and y are inversely proportional to each other when their product xy is a constant (always remains the same). This means that when x increases y will decrease, and vice versa, by an amount such that xy remains the same.

Knowing that the product does not change also allows you to form an equation to find the value of an unknown variable

Example : It takes 4 men 6 hours to repair a road. How long will it take 8 men to do the job if they work at the same rate?

Solution : The number of men is inversely proportional to the time taken to do the job. Let t be the time taken for the 8 men to finish the job. 4 × 6 = 8 × t 24 = 8t t = 3 hours

Usually, you will be able to decide from the question whether the values are directly proportional or inversely proportional.

How To Solve Inverse Proportion Questions?

This video shows how to solve inverse proportion questions. It goes through a couple of examples and ends with some practice questions Example 1: A is inversely proportional to B. When A is 10, B is 2. Find the value of A when B is 8 Example 2: F is inversely proportional to the square of x. When A is 20, B is 3. Find the value of F when x is 5.

How To Use Inverse Proportion To Work Out Problems?

How to use a more advanced form of inverse proportion where the use of square numbers is involved.

More examples to explain direct proportions / variations and inverse proportions / variations

How to solve Inverse Proportion Math Problems on pressure and volume?

In math, an inverse proportion is when an increase in one quantity results in a decrease in another quantity. This video will show how to solve an inverse proportion math problem. Example : The pressure in a piston is 2.0 atm at 25°C and the volume is 4.0L. If the pressure is increased to 6.0 atm at the same temperature, what will be the volume?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Ratio problem solving

Here you will learn about ratio problem solving, including how to set up and solve problems. You will also look at real life ratio word problems.

Students will first learn about ratio problem solving as part of ratio and proportion in 6 th grade and 7 th grade.

What is ratio problem solving?

Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities. They are usually written in the form a : b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are:

What is the ratio involved?
What order are the quantities in the ratio?
What is the total amount / what is the part of the total amount known?
What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that you can use to help you find an answer.

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods you can use when given certain pieces of information.

[FREE] Ratio Problem Solving Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of ratio problem solving. 15 questions with answers to identify areas of strength and support!

When solving ratio word problems, it is very important that you are able to use ratios. This includes being able to use ratio notation.

For example, Charlie and David share some sweets in the ratio of 3 : 5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

You use the ratio to divide 40 sweets into 8 equal parts.

40 \div 8=5

Then you multiply each part of the ratio by 5.

3\times 5:5\times 5=15 : 25

This means that Charlie will get 15 sweets and David will get 25 sweets.

There can be ratio word problems involving different operations and types of numbers.

Here are some examples of different types of ratio word problems:

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
Grade 7 – Ratio and Proportional Relationships (7.RP.A.2) Recognize and represent proportional relationships between quantities.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Ratio problem solving examples

Example 1: part:part ratio.

Within a school, the total number of students who have school lunches to packed lunches is 5 : 7. If 465 students have a school lunch, how many students have a packed lunch?

Within a school, the number of students who have school lunches to packed lunches is \textbf{5 : 7} . If \textbf{465} students have a school lunch, how many students have a packed lunch?

Here you can see that the ratio is 5 : 7, where the first part of the ratio represents school lunches (S) and the second part of the ratio represents packed lunches (P).

You could write this as:

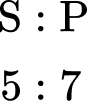
Where the letter above each part of the ratio links to the question.

You know that 465 students have school lunch.

2 Know what you are trying to calculate.

From the question, you need to calculate the number of students that have a packed lunch, so you can now write a ratio below the ratio 5 : 7 that shows that you have 465 students who have school lunches, and p students who have a packed lunch.

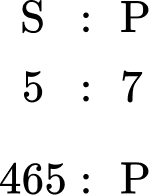
You need to find the value of p.

3 Use prior knowledge to structure a solution.

You are looking for an equivalent ratio to 5 : 7. So you need to calculate the multiplier.

You do this by dividing the known values on the same side of the ratio by each other.

465\div 5 = 93

This means to create an equivalent ratio, you can multiply both sides by 93.

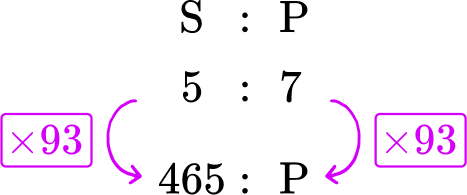
So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

Use the table above to convert £520 \; (GBP) to Euros € \; (EUR).

Use the table above to convert \bf{￡520} \textbf{ (GBP)} to Euros \textbf{€ } \textbf{(EUR)}.

The two values in the table that are important are \text{GBP} and EUR. Writing this as a ratio, you can state,

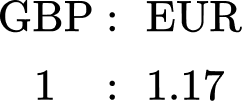
You know that you have £520.

You need to convert GBP to EUR and so you are looking for an equivalent ratio with GBP=£520 and EUR=E.

To get from 1 to 520, you multiply by 520 and so to calculate the number of Euros for £520, you need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520=€608.40.

Example 3: writing a ratio 1 : n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500 \, ml of concentrated plant food must be diluted into 2 \, l of water. Express the ratio of plant food to water, respectively, in the ratio 1 : n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500 \, ml} of concentrated plant food must be diluted into \bf{2 \, l} of water. Express the ratio of plant food to water respectively as a ratio in the form 1 : n.

Using the information in the question, you can now state the ratio of plant food to water as 500 \, ml : 2 \, l. As you can convert liters into milliliters, you could convert 2 \, l into milliliters by multiplying it by 1000.

2 \, l=2000 \, ml

So you can also express the ratio as 500 : 2000 which will help you in later steps.

You want to simplify the ratio 500 : 2000 into the form 1:n.

You need to find an equivalent ratio where the first part of the ratio is equal to 1. You can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

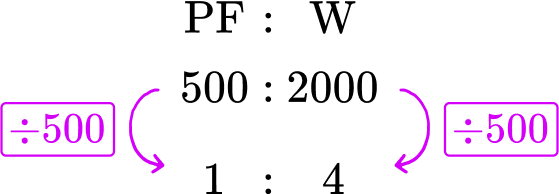
So the ratio of plant food to water in the form 1 : n is 1 : 4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives \$ 8 allowance, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their ages. Kieran is \bf{3} years older than Josh. Luke is twice Josh’s age. If Luke receives \bf{\$ 8} allowance, how much money do the three siblings receive in total?

You can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, you have:

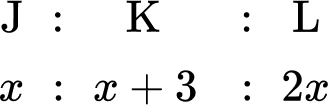
You also know that Luke receives \$ 8.

You want to calculate the total amount of allowance for the three siblings.

You need to find the value of x first. As Luke receives \$ 8, you can state the equation 2x=8 and so x=4.

Now you know the value of x, you can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

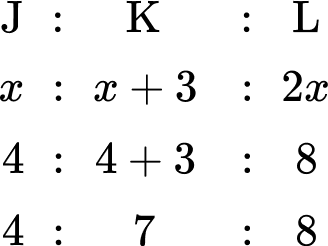
The total amount of allowance is therefore 4+7+8=\$ 19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colors of counters in a bag.

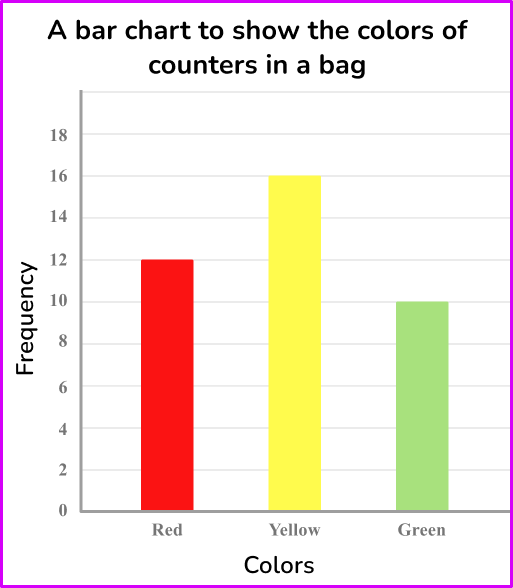
Express this data as a ratio in its simplest form.

From the bar chart, you can read the frequencies to create the ratio.

You need to simplify this ratio.

To simplify a ratio, you need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} & 12 = 1, {\color{red}2}, 3, 4, 6, 12 \\\\ & 16 = 1, {\color{red}2}, 4, 8, 16 \\\\ & 10 = 1, {\color{red}2}, 5, 10 \end{aligned}

HCF(12,16,10) = 2

Dividing all the parts of the ratio by 2, you get

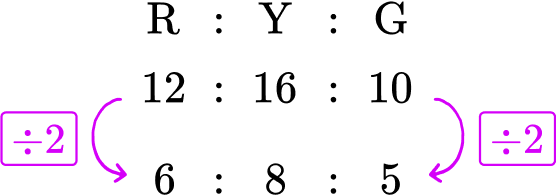
Our solution is 6 : 8 : 5.

Example 6: combining two ratios

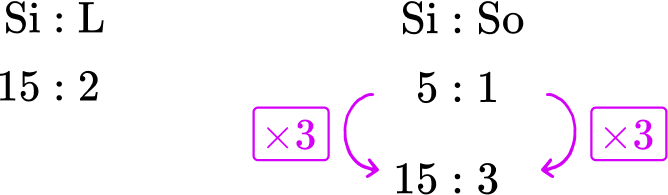
Glass is made from silica, lime and soda. The ratio of silica to lime is 15 : 2. The ratio of silica to soda is 5 : 1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15 : 2}. The ratio of silica to soda is \bf{5 : 1}. State the ratio of silica:lime:soda.

You know the two ratios

You are trying to find the ratio of all 3 components: silica, lime and soda.

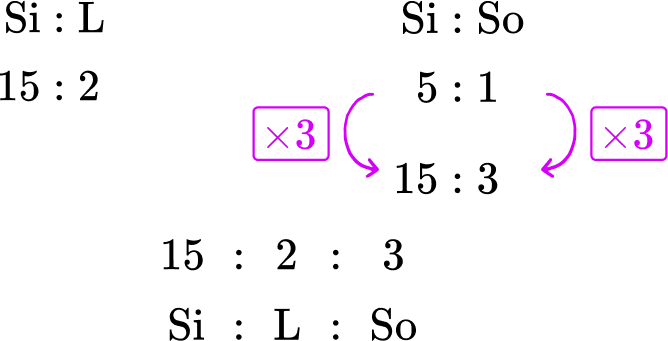
Using equivalent ratios you can say that the ratio of Silica:Soda is equivalent to 15 : 3 by multiplying the ratio by 3.

You now have the same amount of silica in both ratios and so you can now combine them to get the ratio 15 : 2 : 3.

Example 7: using bar modeling

India and Beau share some popcorn in the ratio of 5 : 2. If India has 75 \, g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5 : 2} . If India has \bf{75 \, g} more popcorn than Beau, what was the original quantity?

You know that the initial ratio is 5 : 2 and that India has three more parts than Beau.

You want to find the original quantity.

Drawing a bar model of this problem, you have:

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if you can find out this value, you can then find the total quantity.

From the question, India’s share is 75 \, g more than Beau’s share so you can write this on the bar model.

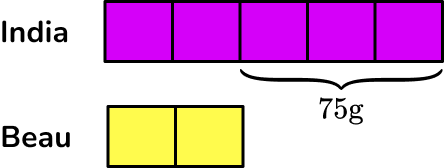
You can find the value of one share by working out 75 \div 3=25 \, g.

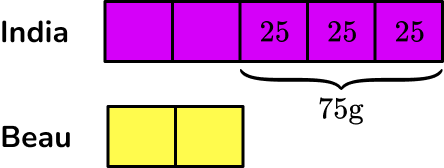
You can fill in each share to be 25 \, g.

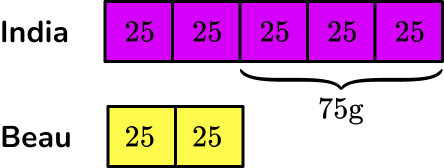
Adding up each share, you get

India=5 \times 25=125 \, g

Beau=2 \times 25=50 \, g

The total amount of popcorn was 125+50=175 \, g.

Teaching tips for ratio problem solving

Continue to remind students that when solving ratio word problems, it’s important to identify the quantities being compared and express the ratio in its simplest form.
Create practice problems for students using the information in your classroom. For example, ask students to find the ratio of boys to the ratio of girls using the total number of students in your classroom, then the school.
To find more practice questions, utilize educational websites and apps instead of worksheets. Some of these may also provide tutorials for struggling students. These can also be helpful for test prep as they are more engaging for students.
Use a variety of numbers in your ratio word problems – whole numbers, fractions, decimals, and mixed numbers – to give students a variety of practice.
Provide students with a step-by-step process for problem solving, like the one shown above, that can be applied to every ratio word problem.

Easy mistakes to make

Mixing units Make sure that all the units in the ratio are the same. For example, in example 6, all the units in the ratio were in milliliters. You did not mix ml and l in the ratio.
Writing ratios in the wrong order For example, the number of dogs to cats is given as the ratio 12 : 13 but the solution is written as 13 : 12.

Counting the number of parts in the ratio, not the total number of shares For example, the ratio 5 : 4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
Ratios of the form \bf{1 : \textbf{n}} The assumption can be incorrectly made that n must be greater than 1, but n can be any number, including a decimal.

Related ratio lessons

Unit rate math
Simplifying ratios
Ratio to fraction
How to calculate exchange rates
Ratio to percent
How to write a ratio
Dividing ratios
How to find the unit rate
Ratio scale
Constant of proportionality

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3 : 8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The ratio of prime numbers to non-prime numbers from 1-200 is 45 : 155. Express this as a ratio in the form 1 : n.

You need to simplify the ratio so that the first number is 1. That means you need to divide each number in the ratio by 45.

45 \div 45=1

155\div{45}=3\cfrac{4}{9}

3. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2 : 3 and the ratio of cloud to rain was 9 : 11. State the ratio that compares sunshine:cloud:rain for the month.

3 \times S : C=6 : 9

4. The angles in a triangle are written as the ratio x : 2x : 3x. Calculate the size of each angle.

You should know that the 3 angles in a triangle always equal 180^{\circ}.

\begin{aligned} & x+2 x+3 x=180 \\\\ & 6 x=180 \\\\ & x=30^{\circ} \\\\ & 2 x=60^{\circ} \\\\ & 3 x=90^{\circ} \end{aligned}

5. A clothing company has a sale on tops, dresses and shoes. \cfrac{1}{3} of sales were for tops, \cfrac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

\cfrac{1}{3}+\cfrac{1}{5}=\cfrac{5+3}{15}=\cfrac{8}{15}

1-\cfrac{8}{15}=\cfrac{7}{15}

6. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75 \, l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

The given ratio in the word problem is 2. 75 \mathrm{~L}: 18^{\circ} \mathrm{K}

Divide 45 by 18 to see the relationship between the two temperatures.

45 \div 18=2.5

45 is 2.5 times greater than 18. So we multiply 2.75 by 2.5 to get the amount of gas.

2.75 \times 2.5=6.875 \mathrm{~l}

Ratio problem solving FAQs

A ratio is a comparison of two or more quantities. It shows how much one quantity is related to another.

A recipe calls for 2 cups of flour and 1 cup of sugar. What is the ratio of flour to sugar? (2 : 1)

In middle school ( 7 th grade and 8 th grade), students transition from understanding basic ratios to working with more complex and real-life applications of ratios and proportions. They gain a deeper understanding of how ratios relate to different mathematical concepts, making them more prepared for higher-level math topics in high school.

The next lessons are

Converting fractions, decimals and percentages

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.