mathematical model of assignment problem

Your Article Library

Assignment problem in linear programming : introduction and assignment model.

ADVERTISEMENTS:

Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.

In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.

1. Assignment Model :

Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.

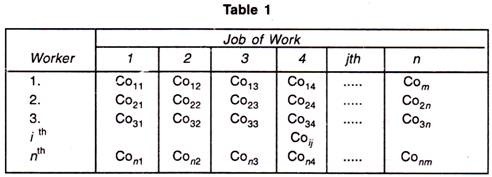
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.

Mathematical Formulation:

Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.

Suppose x jj is a variable which is defined as

1 if the i th job is assigned to j th machine or facility

0 if the i th job is not assigned to j th machine or facility.

Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by

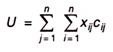
The above definition can be developed into mathematical model as follows:

Determine x ij > 0 (i, j = 1,2, 3…n) in order to

Subjected to constraints

and x ij is either zero or one.

Method to solve Problem (Hungarian Technique):

Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,

1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.

2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.

3. Now, the assignments are made for the reduced table in following manner.

(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.

(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.

(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.

4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:

(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.

(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.

(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.

5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.

6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.

7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.

Related Articles:

• Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
• Linear Programming: Applications, Definitions and Problems

No comments yet.

Leave a reply click here to cancel reply..

You must be logged in to post a comment.

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Assignment Problem: Linear Programming

The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.

In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.

The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.

It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.

"A mathematician is a device for turning coffee into theorems." -Paul Erdos

Formulation of an assignment problem

Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:

The structure of an assignment problem is identical to that of a transportation problem.

To formulate the assignment problem in mathematical programming terms , we define the activity variables as

for i = 1, 2, ..., n and j = 1, 2, ..., n

In the above table, c ij is the cost of performing jth job by ith worker.

Generalized Form of an Assignment Problem

The optimization model is

Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn

subject to x i1 + x i2 +..........+ x in = 1          i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1          j = 1, 2,......., n

x ij = 0 or 1

In Σ Sigma notation

x ij = 0 or 1 for all i and j

An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.

Assumptions in Assignment Problem

• Number of jobs is equal to the number of machines or persons.
• Each man or machine is assigned only one job.
• Each man or machine is independently capable of handling any job to be done.
• Assigning criteria is clearly specified (minimizing cost or maximizing profit).

Share this article with your friends

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem